2024-2025学年上海市浦东新区高二上学期期末教学质量检测数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年上海市浦东新区高二上学期期末教学质量检测数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 340.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 20:43:32 | ||
图片预览



文档简介
2024-2025学年上海市浦东新区高二上学期期末教学质量检测
数学试卷
一、单选题:本题共4小题,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.“平面内有一条直线,则这条直线上的一点必在这个平面内”用符号语言表述是( )
A. B.
C. D.
2.已知为随机事件,与互斥,与互为对立,且,,则( )
A. B. C. D.
3.“中国天眼”为米口径球面射电望远镜
,简称,是具有我国自主知识产权、世界最大单口径、最灵敏的射电望远镜建造“中国天眼”的目的是( )
A. 通过调查获取数据 B. 通过试验获取数据 C. 通过观察获取数据 D. 通过查询获得数据
4.某社区通过公益讲座宣传交通法规为了解讲座效果,随机抽取位居民,分别在讲座前、后各回答一份交通法规知识问卷,满分为分他们得分的茎叶图如图所示“叶”是个位数字,则下列选项叙述错误的是.
A. 讲座后的答卷得分整体上高于讲座前的得分
B. 讲座前的答卷得分分布较讲座后分散
C. 讲座前答卷得分的中位数是
D. 讲座前答卷得分的极差大于讲座后得分的极差
二、填空题:本题共12小题,共54分。
5.两条异面直线所成角的范围是 .
6.记事件的对立事件为,若,则为 .
7.表面积为 的 球的体积是 结果保留
8.已知件产品中有件次品,其余为合格品.现从这件产品中任取件,恰有一件次品的概率为
9.某袋子内装有三种颜色的小球,小明每次从袋子中随机摸出一个小球,观察颜色后再放回,重复了次,得到的信息如下:观察到红色小球次,蓝色小球次如果从这个袋子内任意摸一个小球,这个小球既不是红色也不是蓝色的经验概率为 .
10.已知,若,互斥,则 .
11.若五个数的平均数为,则这五个数的方差等于 .
12.有一组按从小到大顺序排列的数据:,,,,,,若其极差与平均数相等,则这组数据的中位数为 .
13.“石头、剪刀、布”是一种古老的游戏,操作简单,具有极为广泛的群众基础,游戏规则为:石头克剪刀,剪刀克布,布克石头两人参加游戏,若两人都随机出手,则出手次就能分出胜负的概率为 .
14.若平行四边形是用斜二测画法画出的水平放置的平面图形的直观图已知,平行四边形的面积为,则原平面图形中的长度为 .
15.设地球的半径为,若在北纬的纬线图上,则此纬线圈构成的小圆面积为 结果用表示
16.中国有悠久的金石文化,印信是金石文化的代表之一印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”图半正多面体是由两种或两种以上的正多边形围成的多面体半正多面体体现了数学的对称美图是一个棱数为的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为则该半正多面体的棱长为
三、解答题:本题共5小题,共78分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
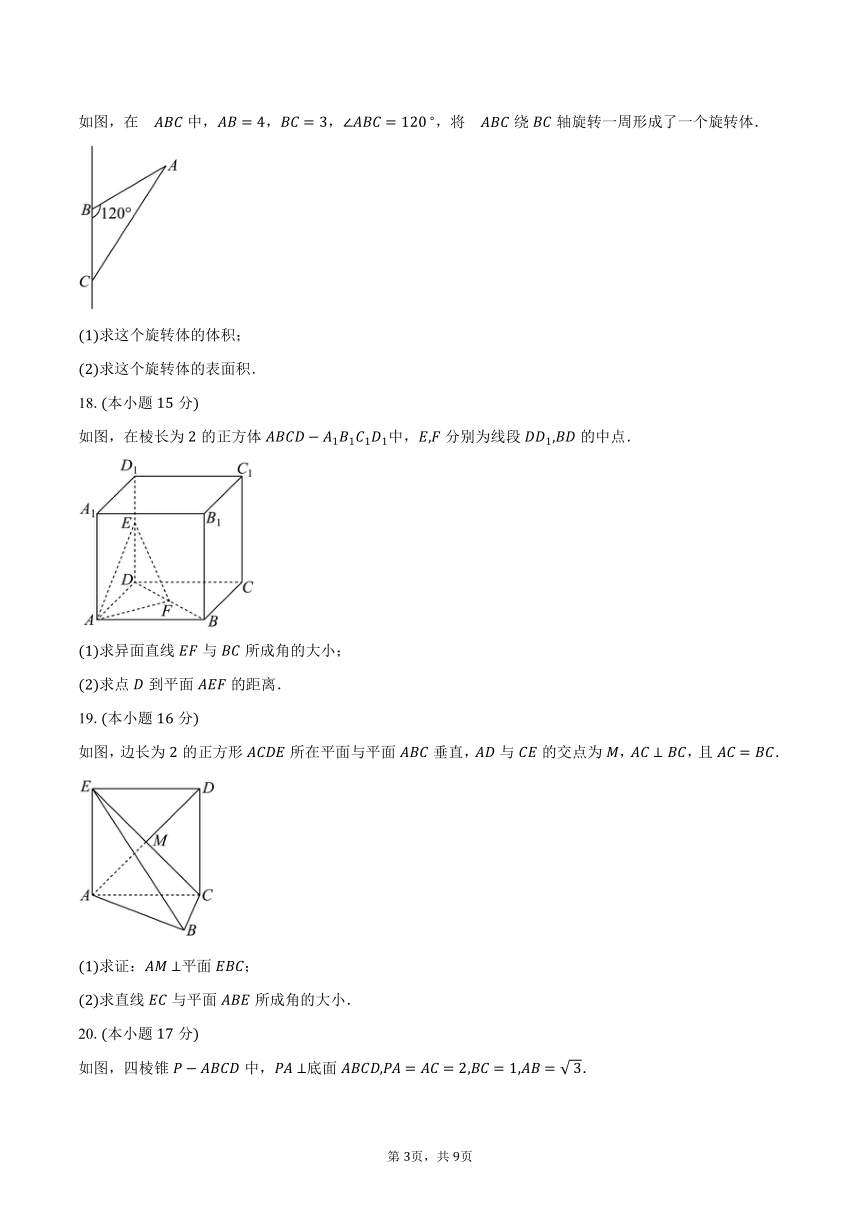
如图,在中,,,,将绕轴旋转一周形成了一个旋转体.
求这个旋转体的体积;
求这个旋转体的表面积.
18.本小题分
如图,在棱长为的正方体中,分别为线段的中点.
求异面直线与所成角的大小;
求点到平面的距离.
19.本小题分
如图,边长为的正方形所在平面与平面垂直,与的交点为,,且.
求证:平面;
求直线与平面所成角的大小.
20.本小题分
如图,四棱锥中,底面.
若,证明:平面;
求二面角的大小.
21.本小题分
年月日,汉江生态城襄阳马拉松在湖北省襄阳市成功举行,志愿者的服务工作是马拉松成功举办的重要保障,襄阳市新时代文明实践中心承办了志愿者选拔的面试工作.现随机抽取了名候选者的面试成绩,并分成五组:第一组,第二组,第三组,第四组,第五组,绘制成如图所示的频率分布直方图.已知第一、二组的频率之和为,第一组和第五组的频率相同.
估计这名候选者面试成绩的平均数和第百分位数;
现从以上各组中用分层随机抽样的方法选取人,担任本市的宣传者.若本市宣传者中第二组面试者的面试成绩的平均数和方差分别为和,第四组面试者的面试成绩的平均数和方差分别为和,据此估计这次第二组和第四组所有面试者的面试成绩的方差.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.或
13.
14.
15.
16.
17.【小问答案】
绕轴旋转一周,形成的几何体一个大圆锥挖去一个小圆锥余下的部分
如图所示在中,,,,
.
设旋转体的底面面积为,旋转得到同底的两圆锥的侧面积分别为和,则旋转体的体积
.
【小问答案】
由得旋转体的表面积
.
18.【小问答案】
连接,,因为分别为线段的中点,
所以,故异面直线与所成角为;
又平面,平面,
所以,
所以,
故异面直线与所成的角为.
【小问答案】
在正方体中,分别为线段的中点,
所以平面,且
因为是线段的中点,
所以,
故三棱锥的体积;
因为分别为线段的中点,
所以,
又因为,
所以在中满足,故为直角三角形,
则,
设点到平面的距离为,
则三棱锥的体积,解得,
因此点到平面的距离为.
19.【小问答案】
由是正方形,则,
因为面面,面面,,面,
所以面,又面,
所以,
又因为,平面,平面,
所以平面.
【小问答案】
过作交于,连接,
因为是正方形,则,
因为面面,面面,面,
所以面,又面,
所以,
又因为,,面,面,
所以面,
所以即为直线与平面所成角,
因为正方形边长为,,,
所以,,
所以,
因为 ,
所以,即直线与平面所成角的大小为.
20.【小问答案】
因为底面,面,
所以,
又因为,,面,面,
所以面,
因为,
所以,故,
又因为 底面,面,
所以,
又,面,面,
所以面,
所以,又平面,平面,
所以平面.
【小问答案】
由可知,面,
因为面,
所以,
又因为,
所以即为二面角的平面角,
在中,,
所以,
所以,
所以二面角的大小为.
21.解:由题意可知
解得
可知每组的频率依次为:
,,,,,
所以平均数为
,
因为,
设第百分位数为,则
则,
解得,故第百分位数为;
设第二组、第四组面试者的面试成绩的平均数与方差分别为,
且两组频率之比为,
则第二组和第四组所有面试者的面试成绩的平均数
,
第二组和第四组所有面试者的面试成绩的方差
,
故估计第二组和第四组所有面试者的面试成绩的方差是.
第1页,共1页
数学试卷
一、单选题:本题共4小题,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.“平面内有一条直线,则这条直线上的一点必在这个平面内”用符号语言表述是( )
A. B.
C. D.
2.已知为随机事件,与互斥,与互为对立,且,,则( )
A. B. C. D.
3.“中国天眼”为米口径球面射电望远镜
,简称,是具有我国自主知识产权、世界最大单口径、最灵敏的射电望远镜建造“中国天眼”的目的是( )
A. 通过调查获取数据 B. 通过试验获取数据 C. 通过观察获取数据 D. 通过查询获得数据
4.某社区通过公益讲座宣传交通法规为了解讲座效果,随机抽取位居民,分别在讲座前、后各回答一份交通法规知识问卷,满分为分他们得分的茎叶图如图所示“叶”是个位数字,则下列选项叙述错误的是.
A. 讲座后的答卷得分整体上高于讲座前的得分
B. 讲座前的答卷得分分布较讲座后分散
C. 讲座前答卷得分的中位数是
D. 讲座前答卷得分的极差大于讲座后得分的极差
二、填空题:本题共12小题,共54分。
5.两条异面直线所成角的范围是 .
6.记事件的对立事件为,若,则为 .
7.表面积为 的 球的体积是 结果保留
8.已知件产品中有件次品,其余为合格品.现从这件产品中任取件,恰有一件次品的概率为
9.某袋子内装有三种颜色的小球,小明每次从袋子中随机摸出一个小球,观察颜色后再放回,重复了次,得到的信息如下:观察到红色小球次,蓝色小球次如果从这个袋子内任意摸一个小球,这个小球既不是红色也不是蓝色的经验概率为 .
10.已知,若,互斥,则 .
11.若五个数的平均数为,则这五个数的方差等于 .
12.有一组按从小到大顺序排列的数据:,,,,,,若其极差与平均数相等,则这组数据的中位数为 .
13.“石头、剪刀、布”是一种古老的游戏,操作简单,具有极为广泛的群众基础,游戏规则为:石头克剪刀,剪刀克布,布克石头两人参加游戏,若两人都随机出手,则出手次就能分出胜负的概率为 .
14.若平行四边形是用斜二测画法画出的水平放置的平面图形的直观图已知,平行四边形的面积为,则原平面图形中的长度为 .
15.设地球的半径为,若在北纬的纬线图上,则此纬线圈构成的小圆面积为 结果用表示
16.中国有悠久的金石文化,印信是金石文化的代表之一印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”图半正多面体是由两种或两种以上的正多边形围成的多面体半正多面体体现了数学的对称美图是一个棱数为的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为则该半正多面体的棱长为
三、解答题:本题共5小题,共78分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
如图,在中,,,,将绕轴旋转一周形成了一个旋转体.
求这个旋转体的体积;
求这个旋转体的表面积.
18.本小题分
如图,在棱长为的正方体中,分别为线段的中点.
求异面直线与所成角的大小;
求点到平面的距离.
19.本小题分
如图,边长为的正方形所在平面与平面垂直,与的交点为,,且.
求证:平面;
求直线与平面所成角的大小.
20.本小题分
如图,四棱锥中,底面.
若,证明:平面;
求二面角的大小.
21.本小题分
年月日,汉江生态城襄阳马拉松在湖北省襄阳市成功举行,志愿者的服务工作是马拉松成功举办的重要保障,襄阳市新时代文明实践中心承办了志愿者选拔的面试工作.现随机抽取了名候选者的面试成绩,并分成五组:第一组,第二组,第三组,第四组,第五组,绘制成如图所示的频率分布直方图.已知第一、二组的频率之和为,第一组和第五组的频率相同.
估计这名候选者面试成绩的平均数和第百分位数;
现从以上各组中用分层随机抽样的方法选取人,担任本市的宣传者.若本市宣传者中第二组面试者的面试成绩的平均数和方差分别为和,第四组面试者的面试成绩的平均数和方差分别为和,据此估计这次第二组和第四组所有面试者的面试成绩的方差.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.或
13.
14.
15.
16.
17.【小问答案】
绕轴旋转一周,形成的几何体一个大圆锥挖去一个小圆锥余下的部分
如图所示在中,,,,
.
设旋转体的底面面积为,旋转得到同底的两圆锥的侧面积分别为和,则旋转体的体积
.
【小问答案】
由得旋转体的表面积
.
18.【小问答案】
连接,,因为分别为线段的中点,
所以,故异面直线与所成角为;
又平面,平面,
所以,
所以,
故异面直线与所成的角为.
【小问答案】
在正方体中,分别为线段的中点,
所以平面,且
因为是线段的中点,
所以,
故三棱锥的体积;
因为分别为线段的中点,
所以,
又因为,
所以在中满足,故为直角三角形,
则,
设点到平面的距离为,
则三棱锥的体积,解得,
因此点到平面的距离为.
19.【小问答案】
由是正方形,则,
因为面面,面面,,面,
所以面,又面,
所以,
又因为,平面,平面,
所以平面.
【小问答案】
过作交于,连接,
因为是正方形,则,
因为面面,面面,面,
所以面,又面,
所以,
又因为,,面,面,
所以面,
所以即为直线与平面所成角,
因为正方形边长为,,,
所以,,
所以,
因为 ,
所以,即直线与平面所成角的大小为.
20.【小问答案】
因为底面,面,
所以,
又因为,,面,面,
所以面,
因为,
所以,故,
又因为 底面,面,
所以,
又,面,面,
所以面,
所以,又平面,平面,
所以平面.
【小问答案】
由可知,面,
因为面,
所以,
又因为,
所以即为二面角的平面角,
在中,,
所以,
所以,
所以二面角的大小为.
21.解:由题意可知
解得
可知每组的频率依次为:
,,,,,
所以平均数为
,
因为,
设第百分位数为,则
则,
解得,故第百分位数为;
设第二组、第四组面试者的面试成绩的平均数与方差分别为,
且两组频率之比为,
则第二组和第四组所有面试者的面试成绩的平均数
,
第二组和第四组所有面试者的面试成绩的方差
,
故估计第二组和第四组所有面试者的面试成绩的方差是.
第1页,共1页
同课章节目录
