2024-2025学年上海市青浦高级中学高二(上)期末数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年上海市青浦高级中学高二(上)期末数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 125.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 20:44:54 | ||
图片预览



文档简介
2024-2025学年上海市青浦高级中学高二(上)期末数学试卷
一、单选题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,只有一项是符合题目要求的。
1.对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图,则该样本的中位数、众数分别是( )
A. , B. , C. , D. ,
2.空间中有两个不同的平面,和两条不同的直线,,则下列说法中正确的是( )
A. 若,,,则
B. 若,,,则
C. 若,,,则
D. 若,,,则
3.已知等差数列的前项和为,,,则使取得最大值时的值为( )
A. B. C. D.
4.已知点在确定的平面内,是平面外任意一点,满足,且,,则的最小值为( )
A. B. C. D.
二、填空题:本题共12小题,每小题5分,共60分。
5.直线的倾斜角为______.
6.为了考察某区万名高一年级学生数学知识与能力测试的成绩,从中抽取本试卷,每本试卷份,那么样本容量是______.
7.已知向量,,,则 ______.
8.,,三个数成等比数列,其中,,则 ______.
9.甲、乙两人各进行次射击,如果两人击中目标的概率分别为和,则其中恰有人击中目标的概率是______.
10.如果圆锥的底面圆半径为,母线长为,则该圆锥的侧面积为______.
11.已知直线:与直线:平行,则 ______.
12.在空间直角坐标系中,点为平面外一点,点为平面内一点若平面的一个法向量为,则点到平面的距离是______.
13.若将两个半径为的铁球熔化后铸成一个球,则该球的表面积为______.
14.某车间的质检员利用随机数表对生产的个零件进行抽样测试,先将个零件进行编号,编号分别为,,,,从中选取个个体组成样本,下面提供随机数表的第行到第行:
若从表中第行第列开始向右依次读取数据,则得到的第个样本编号是______.
15.定义两个相交平面夹角为两个平面所组成的四个二面角的最小值已知平面与所成的角为,为,外一定点,过点的一条直线与,所成的角都是,则这样的直线有______.
16.已知正四面体的边长为,是空间一点,若,则的最小值为______.
三、解答题:本题共5小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知圆的圆心为,若圆经过直线:,:的交点.
求圆的标准方程;
直线:与圆交于,两点,且,求直线的方程.
18.本小题分
为加强学生睡眠监测督导,学校对高中三个年级学生的日均睡眠时间进行调查根据分层随机抽样法,学校在高一、高二和高三年级中共抽取了名学生的日均睡眠时间作为样本,其中高一人,高二人已知该校高三年级一共人.
学校高中三个年级一共有多少个学生?
若抽取名学生的样本极差为,数据如表所示其中,是正整数
日均睡眠时间小时
学生数量
求该样本的第百分位数.
19.本小题分
如图,已知点在圆柱的底面圆上,,圆的直径,圆柱的高.
求圆柱的表面积与体积;
求直线与所成的角.
20.本小题分
如图,已知,,,直线.
证明直线经过某一定点,并求此定点坐标;
若直线等分的面积,求直线的一般式方程;
若,李老师站在点用激光笔照出一束光线,依次由反射点为、反射点为反射后,光斑落在点,求入射光线的直线方程.
21.本小题分
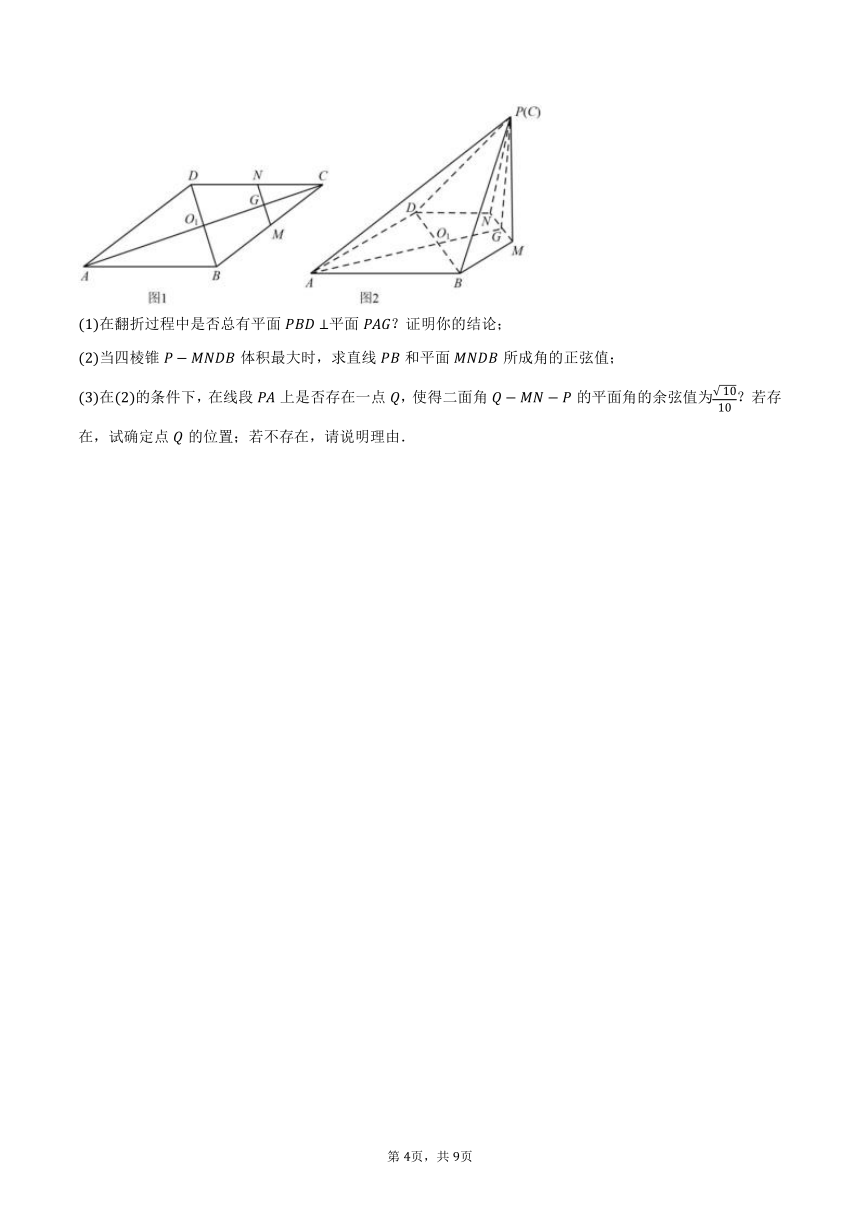
如图,在边长为的菱形中,,点,分别是边,的中点,,沿将翻折到的位置,连接,,,得到如图所示的五棱锥.
在翻折过程中是否总有平面平面?证明你的结论;
当四棱锥体积最大时,求直线和平面所成角的正弦值;
在的条件下,在线段上是否存在一点,使得二面角的平面角的余弦值为?若存在,试确定点的位置;若不存在,请说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:联立,
解得,
故直线和的交点为,
,
故圆的标准方程为;
直线:与圆交于,两点,且,
则,
解得,
故直线的方程为.
18.解:根据题意,在抽取的名学生中,高三年级的人数为,
设高中三个年级一共有个学生,,
所以,
解得,
所以高中三个年级一共有个学生;
因为抽取名学生的样本极差为,,
所以,可得,
因为,
可得,
因为,
所以该样本的第百分位数为.
19.解:根据题意,因为是圆的直径,则,
圆柱的表面积,
圆柱的体积;
根据题意,因为,所以与所成角即为与所成角,
连结因为是圆的直径,所以因为,
所以,.
又因为,所以,,
则,
,即直线与所成的角为.
20.解:直线可化为,
令,解得,故直线经过的定点坐标为;
因为,,,所以,
由题意得直线方程为,
故直线经过的定点在直线上,所以,
设直线与交于点,所以,
即,所以,
设,所以,即,
所以,,所以,
将点坐标代入直线的方程,解得,
所以直线的方程为;
设关于的对称点,关于的对称点,
直线的方程为,即,
直线的方程为,所以,
解得,所以,
由题意得,,,四点共线,,由对称性得,
所以入射光线的直线方程为,
即.
21.在翻折过程中总有平面平面,
证明:点,分别是边,的中点,,
又因为菱形中 ,是等边三角形,
是的中点,,
菱形的对角线互相垂直,,,
,平面,平面,
平面,平面,平面,平面平面.
解:由题意知,四边形为等腰梯形,且,,,
所以等腰梯形的面积,
要使得四棱锥 体积最大,只要点到平面的距离最大即可,
当平面时,点到平面的距离的最大值为,
此时四棱锥 体积的最大值为,
连接,则直线和平面所成角的为 ,
在中,,,由勾股定理得:.
.
解:假设符合题意的点存在.
以为坐标原点,,,所在直线分别为轴、轴、轴,建立如图所示空间直角坐标系,
则,,,,因为平面,故平面的一个法向量为,
设,,,
故,,,
平面的一个法向量为,则,,
即,令,所以,
即,
则平面的一个法向量,设二面角的平面角为,
所以,解得:,
故符合题意的点存在,且为线段的中点.
第1页,共1页
一、单选题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,只有一项是符合题目要求的。
1.对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图,则该样本的中位数、众数分别是( )
A. , B. , C. , D. ,
2.空间中有两个不同的平面,和两条不同的直线,,则下列说法中正确的是( )
A. 若,,,则
B. 若,,,则
C. 若,,,则
D. 若,,,则
3.已知等差数列的前项和为,,,则使取得最大值时的值为( )
A. B. C. D.
4.已知点在确定的平面内,是平面外任意一点,满足,且,,则的最小值为( )
A. B. C. D.
二、填空题:本题共12小题,每小题5分,共60分。
5.直线的倾斜角为______.
6.为了考察某区万名高一年级学生数学知识与能力测试的成绩,从中抽取本试卷,每本试卷份,那么样本容量是______.
7.已知向量,,,则 ______.
8.,,三个数成等比数列,其中,,则 ______.
9.甲、乙两人各进行次射击,如果两人击中目标的概率分别为和,则其中恰有人击中目标的概率是______.
10.如果圆锥的底面圆半径为,母线长为,则该圆锥的侧面积为______.
11.已知直线:与直线:平行,则 ______.
12.在空间直角坐标系中,点为平面外一点,点为平面内一点若平面的一个法向量为,则点到平面的距离是______.
13.若将两个半径为的铁球熔化后铸成一个球,则该球的表面积为______.
14.某车间的质检员利用随机数表对生产的个零件进行抽样测试,先将个零件进行编号,编号分别为,,,,从中选取个个体组成样本,下面提供随机数表的第行到第行:
若从表中第行第列开始向右依次读取数据,则得到的第个样本编号是______.
15.定义两个相交平面夹角为两个平面所组成的四个二面角的最小值已知平面与所成的角为,为,外一定点,过点的一条直线与,所成的角都是,则这样的直线有______.
16.已知正四面体的边长为,是空间一点,若,则的最小值为______.
三、解答题:本题共5小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知圆的圆心为,若圆经过直线:,:的交点.
求圆的标准方程;
直线:与圆交于,两点,且,求直线的方程.
18.本小题分
为加强学生睡眠监测督导,学校对高中三个年级学生的日均睡眠时间进行调查根据分层随机抽样法,学校在高一、高二和高三年级中共抽取了名学生的日均睡眠时间作为样本,其中高一人,高二人已知该校高三年级一共人.
学校高中三个年级一共有多少个学生?
若抽取名学生的样本极差为,数据如表所示其中,是正整数
日均睡眠时间小时
学生数量
求该样本的第百分位数.
19.本小题分
如图,已知点在圆柱的底面圆上,,圆的直径,圆柱的高.
求圆柱的表面积与体积;
求直线与所成的角.
20.本小题分
如图,已知,,,直线.
证明直线经过某一定点,并求此定点坐标;
若直线等分的面积,求直线的一般式方程;
若,李老师站在点用激光笔照出一束光线,依次由反射点为、反射点为反射后,光斑落在点,求入射光线的直线方程.
21.本小题分
如图,在边长为的菱形中,,点,分别是边,的中点,,沿将翻折到的位置,连接,,,得到如图所示的五棱锥.
在翻折过程中是否总有平面平面?证明你的结论;
当四棱锥体积最大时,求直线和平面所成角的正弦值;
在的条件下,在线段上是否存在一点,使得二面角的平面角的余弦值为?若存在,试确定点的位置;若不存在,请说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:联立,
解得,
故直线和的交点为,
,
故圆的标准方程为;
直线:与圆交于,两点,且,
则,
解得,
故直线的方程为.
18.解:根据题意,在抽取的名学生中,高三年级的人数为,
设高中三个年级一共有个学生,,
所以,
解得,
所以高中三个年级一共有个学生;
因为抽取名学生的样本极差为,,
所以,可得,
因为,
可得,
因为,
所以该样本的第百分位数为.
19.解:根据题意,因为是圆的直径,则,
圆柱的表面积,
圆柱的体积;
根据题意,因为,所以与所成角即为与所成角,
连结因为是圆的直径,所以因为,
所以,.
又因为,所以,,
则,
,即直线与所成的角为.
20.解:直线可化为,
令,解得,故直线经过的定点坐标为;
因为,,,所以,
由题意得直线方程为,
故直线经过的定点在直线上,所以,
设直线与交于点,所以,
即,所以,
设,所以,即,
所以,,所以,
将点坐标代入直线的方程,解得,
所以直线的方程为;
设关于的对称点,关于的对称点,
直线的方程为,即,
直线的方程为,所以,
解得,所以,
由题意得,,,四点共线,,由对称性得,
所以入射光线的直线方程为,
即.
21.在翻折过程中总有平面平面,
证明:点,分别是边,的中点,,
又因为菱形中 ,是等边三角形,
是的中点,,
菱形的对角线互相垂直,,,
,平面,平面,
平面,平面,平面,平面平面.
解:由题意知,四边形为等腰梯形,且,,,
所以等腰梯形的面积,
要使得四棱锥 体积最大,只要点到平面的距离最大即可,
当平面时,点到平面的距离的最大值为,
此时四棱锥 体积的最大值为,
连接,则直线和平面所成角的为 ,
在中,,,由勾股定理得:.
.
解:假设符合题意的点存在.
以为坐标原点,,,所在直线分别为轴、轴、轴,建立如图所示空间直角坐标系,
则,,,,因为平面,故平面的一个法向量为,
设,,,
故,,,
平面的一个法向量为,则,,
即,令,所以,
即,
则平面的一个法向量,设二面角的平面角为,
所以,解得:,
故符合题意的点存在,且为线段的中点.
第1页,共1页
同课章节目录
