湖北省仙桃市2024-2025学年上学期九年级期末考试数学试题(PDF版,含答案)
文档属性
| 名称 | 湖北省仙桃市2024-2025学年上学期九年级期末考试数学试题(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 21:58:02 | ||
图片预览




文档简介
仙桃市 2024年秋季学期期末质量监测
九年级数学试题
(本试题共 6页,满分 120分,考试时间 120分钟)
注意事项:
1、答题前,考生务必将姓名、准考证号填写在答题卡上;并将“条形码”粘贴在答题卡指
定位置。
2、每道选择题的答案选出后,请用 2B铅笔把答题卡上对应的答案标号涂黑。如需改动,
先用橡皮擦干净后,再选涂其他答案标号。非选择题的答案也应写在答题卡对应的区域内,
写在试卷上无效。
3、考试结束,请将本试卷和答题卡一并上交。
一、选择题(本大题共 10个小题,每小题 3分,满分 30分)
1.2025年 1月 5日,是二十四节气的小寒.二十四节气是中国劳动人民独创的文化遗产,能
反映季节的变化,指导农事活动.下面四幅图片分别代表“立夏”、“大雪”、“小寒”、“立
春”,其中是中心对称图形的是
A B C D
2.若方程 x2-(k-1)x+2=0有一个根是 x=-1,则 k的值是
A.-2 B.-1 C.1 D.2
3.下列事件中是必然事件的是
A.床前明月光 B.大漠孤烟直 C.黄河入海流 D.手可摘星辰
4.关于二次函数 y=(x+2)2+6的图象,下列结论正确的是
A.开口向下 B.对称轴是 x=2
C.与 y轴交于点(0,6) D.当 x<-2时,y随 x的增大而减小
5.设 a,b是方程 x2+x-2024=0的两个实数根,则 a2+2a+b的值为
A.2022 B.2023 C.2024 D.2025
6.汽车刹车后行驶的距离 S(单位:米)关于行驶时间 t(单位:秒)的函数关系式是 S=6t
-t2,则该汽车从刹车到停止所用时间为
A.3秒 B.6秒 C.9秒 D.10秒
7.用半径为 30,圆心角为 120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面半径是
A.20 B.15 C.10 D.5
九年级数学试卷 第 1 页 (共 6 页)
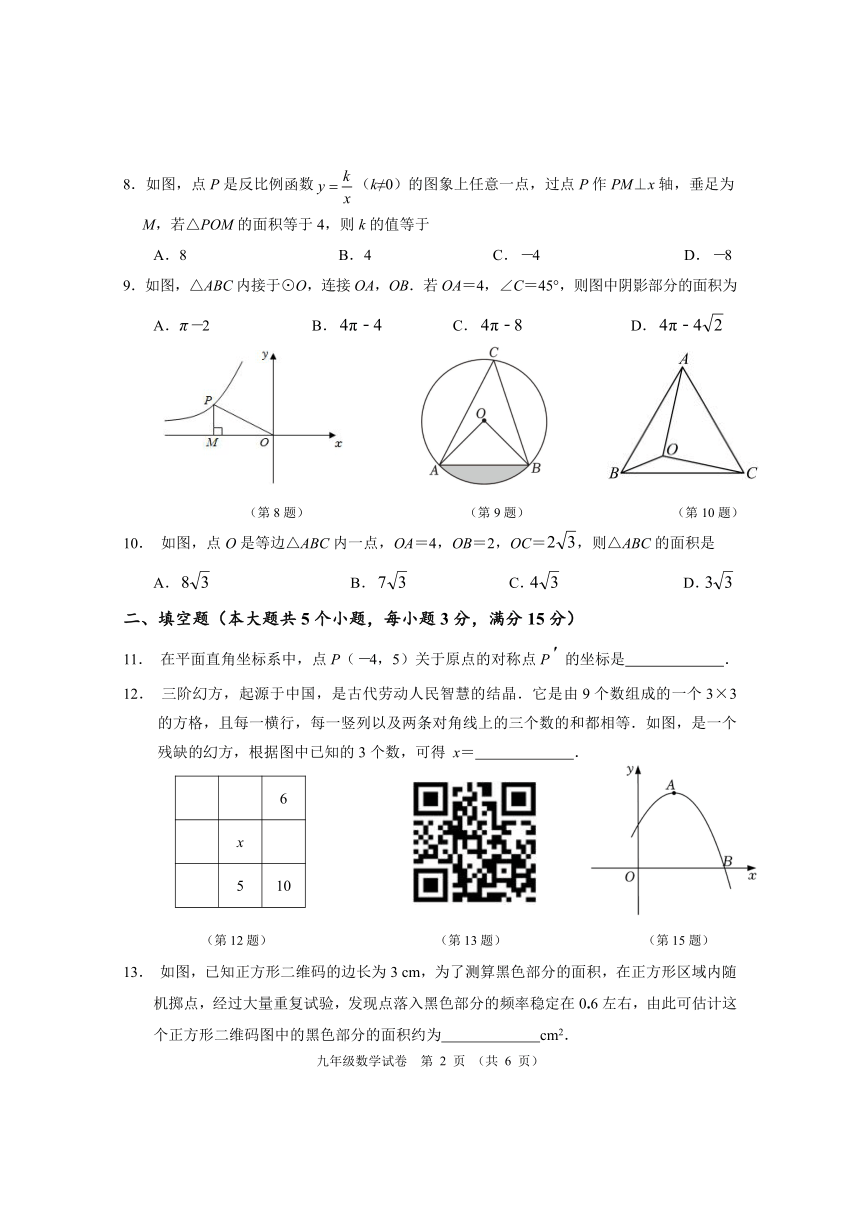
8 k.如图,点 P是反比例函数 y (k≠0)的图象上任意一点,过点 P作 PM⊥x轴,垂足为
x
M,若△POM的面积等于 4,则 k的值等于
A.8 B.4 C.-4 D.-8
9.如图,△ABC内接于⊙O,连接 OA,OB.若 OA=4,∠C=45°,则图中阴影部分的面积为
A.π-2 B. 4π-4 C. 4π-8 D. 4π-4 2
(第 8题) (第 9题) (第 10题)
10. 如图,点 O是等边△ABC内一点,OA=4,OB=2,OC=2 3,则△ABC的面积是
A.8 3 B.7 3 C.4 3 D.3 3
二、填空题(本大题共 5个小题,每小题 3分,满分 15分)
11. 在平面直角坐标系中,点 P(-4,5)关于原点的对称点 P ′ 的坐标是 .
12. 三阶幻方,起源于中国,是古代劳动人民智慧的结晶.它是由 9 个数组成的一个 3×3
的方格,且每一横行,每一竖列以及两条对角线上的三个数的和都相等.如图,是一个
残缺的幻方,根据图中已知的 3个数,可得 x= .
6
x
5 10
(第 12题) (第 13题) (第 15题)
13. 如图,已知正方形二维码的边长为 3 cm,为了测算黑色部分的面积,在正方形区域内随
机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在 0.6左右,由此可估计这
个正方形二维码图中的黑色部分的面积约为 cm2.
九年级数学试卷 第 2 页 (共 6 页)
14. 我国南宋数学家杨辉在《田亩比类乘除算法》中记录了这样一个问题:“直田积八百六
十四步,只云阔与长共六十步,问阔及长各几步?”其大意是:矩形面积是 864平步,
其中宽与长的和为 60 步,问宽和长各几步?若设矩形的长为 x 步,根据题意可列方
程 .
15. 抛物线 y=ax2+bx+c的顶点为 A(2,m),且经过点 B(5,0),其部分图象如图所示.对
于此抛物线有如下四个结论:①abc<0;②a-b+c<0;③4a+b=0;④若此抛物线经过
点 C(-2,n),则不等式 ax2+bx+c-n<0的解集是-2<x<6.其中所有正确结论的序
号是 .
三、解答题(本大题共 9个小题,满分 75分)
16.(6分)
解方程:(1)x2-6x-7=0; (2)x(x-2)=3x-6.
17.(6分)
某校开展数学趣味知识竞赛活动,要求参赛学生从 “A:幻方; B:数独; C :魔方”
三个项目中选择 1~2个项目参加比赛.现将“A ”“ B ”“ C ”分别写在 3张无差别
的不透明的卡片正面上,洗匀后正面向下放在桌面上,等候参赛选手随机抽取.
(1)小明同学选择一项参赛,他随机抽取一张卡片,恰好选中项目“A ”是
事件;(填“确定”或“随机”)
(2)小亮同学选择两项参赛,他随机一次性抽取两张卡片,求都没有抽到项目“ B ”的
概率.
18.(6分)
如图,正方形网格中,每个小正方形的边长都是一个单
位长度,在平面直角坐标系中,△ABC的三个顶点坐标
A(-2,0),B(-5,-3),C(0,-5)都在格点上.
(1)若△ABC 平移后得到△A1B1C1,当 A1 的坐标为
(4,4),画出△A1B1C1,并写出 B1,C1的坐标;
(2)将△A1B1C1绕原点逆时针旋转 90°得到△A2B2C2,
画出△A2B2C2,并直接写出点 A2的坐标;
(3)求△A2B2C2的面积.
九年级数学试卷 第 3 页 (共 6 页)
19.(8分)
已知关于 x的一元二次方程 x2+(2m+1)x+m2-1=0有两个不相等的实数根.
(1)求 m的取值范围;
(2)设 x1,x2是方程的两个根且 x12+x22+x1x2-6=0,求 m的值.
20.(8分)
如图,PA切⊙O于点 A,AB是⊙O直径,C是⊙O上一点,PA PC AB,连接 PO交 AC
于点 D.
(1)求证:PC是⊙O的切线; A
(2)若 BC 2,求 AB的长.
P D O
C B
21.(8分)
如图,已知一次函数 y1
m
ax+b与反比例函数 y2 x 的图象在第一,第三象限分别交于
A(1,4), B(n, -1)两点,直线 AB与 y轴,x轴分别交于 C,D两点.
(1)求一次函数和反比例函数关系式; y
(2)比较大小: AD BC(填“<”,“ ”或“>” );
(3)当 y1>y2时,请直接写出 x的取值范围. A
C
D O x
B
九年级数学试卷 第 4 页 (共 6 页)
22.(10分)
根据以下素材,探索完成任务.
如何设计喷灌器喷水口的升降方案
随着自动化设备的普及,家庭庭院也引
入自动喷灌系统.图 1中某庭院内有一
个可垂直升降的草坪喷灌器,从喷水口
素 喷出的水柱成抛物线形.图 2是该喷灌
材 器 OA喷水时的截面示意图,喷水口 A
1 点离地高度 AO=0.25m,喷出的水柱在
离喷水口水平距离为 2m处达到最高,
高度为 0.45m,且水柱刚好落在庭院围
墙和地面的交界 B点处.
为了美化庭院,准备在庭院内沿围墙建
花坛种花,花坛高 DC =0.4m,宽 BC=DE
=0.8m,侧面用大理石包围,矩形 BCDE
素
是花坛截面,如图 3.调整喷水口的高
材
2 度,喷出的水柱形状与原来相同且随之
上下平移,使花坛的上方从 D到 E的区
域刚好都能被水柱浇灌(大理石厚度不
计),从而达到给花坛喷灌的效果.
解决问题
在图 2中,建立合适的平面直角坐标系,求
任务 1 确定水柱的形状
抛物线的解析式?
任务 2 确定喷灌器的位置 求喷灌器OA与围墙的水平距离OB是多少?
调整喷水口的高度,使花坛的上方 DE边上
任务 3 拟定喷头升降方案 刚好都能被水柱喷灌,请直接写出喷水口距
离地面高度的取值范围.
九年级数学试卷 第 5 页 (共 6 页)
23.(11分)
【问题提出】
在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点 D在边 AB上,探究
ED与 EB数量关系.
【问题探究】
(1)如图 1,当点 E在边 BC上时,猜想 ED与 EB数量关系,并加以证明;
(2)如图 2,当点 E在△ABC内部时,证明(1)中的结论仍然成立;
【问题拓展】
(3)如图 3,当点 E在△ABC外部时,EF⊥AB于点 F,过点 E作 EG∥AB,交线段 AC
的延长线于点 G,AG=5CG,BF=3,请直接写出 CG的长.
C G EC C
E
E
A D B A D B
图 1 2 A D F B图 图 3
24.(12分)
如图所示,抛物线 y=ax2+2x+c的对称轴为 x=1,与 x轴交于 A,B两点,与 y轴交于
点 C(0,5),直线 y=-x+1与该抛物线交于 D,E两点(点 D在点 E的左侧).
(1)求该抛物线的解析式及 D,E两点的坐标;
(2)如图 2,将位于直线 DE上方的抛物线沿着直线 DE翻折,点 P是 DE上方的抛物
线上的一动点,点 P的对应点为点 Q,连接 PQ交 DE于点 G.
①当四边形 DPEQ是菱形时,请直接写出点 P的坐标;
②在点 P的运动过程中,请求出线段 PQ的最大值.
图 1 图 2
九年级数学试卷 第 6 页 (共 6 页)
仙桃市 2024 年秋季学期期末质量监测
九年级数学考答案及评分说明
说明:本评分说明一般只给出一种解法,对其他解法,只要推理严谨,运算合理,结果正确,均给满分;
对部分正确的,参照此评分说明,酌情给分.
一、选择题(每小题 3 分,满分 30 分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C D B A C D C B
二、填空题(每小题 3 分,共 15 分)
11.(4,-5); 12.9; 13.5.4 ;
14.x(60- x)=864; 15.①③.(每填对 1个得 2分,填对 2个得 3分)
三、解答题(共 75 分)
16.解:(1)x1=-1,x2=7; -----------------------3分
(2)x1=2,x2=3. -----------------------6分
17.解:(1)随机; -----------------------2分
1
(2)P(都没有抽到项目“B”)= . -----------------------6 分3
18.解:(1)如图所示,△A1B1C1即为所求,B1(1,1)C1(6,-1); -----------------------2 分
(2)如图所示,△A2B2C2即为所求,点 A2(-4,4); -----------------------4分
(3)S△A2B2C2=S△ABC=10.5. -----------------------6 分
5
19.解:(1)m的取值范围是 m> ; -----------------------4分
4
2
(2)m= . -----------------------8分
3
九年级数学答案 第 1 页 共 6 页
A
20.(1)证明:如图,连接 OC,
∵ PA是⊙O的切线,
P D O
∴PA⊥OA .
∴∠PAO 90° .
C B
∵ OC OA,PC PA,OP OP.
∴△POC≌△POA(SSS). -----------------------2分
∴ ∠PCO ∠PAO 90° .
∴ OD⊥CD .
又点 C在⊙O上,
∴ PC是⊙O的切线; -----------------------4分
(2) 解: 如图,由(1)可证:
∠PDA ∠ACB 90°,∠APD ∠BAC.
又 PA AB,
∴△PAD≌△ABC(AAS). -----------------------6分
∴ AD BC 2,AC 2AD 4.
在 Rt△ABC中,由勾股定理可得:
AB 22 42 2 5. -----------------------8分
m
21. 解:(1)将 A(1, 4)代入 y (m为常数,m 0)x 可得:m 4.
4
∴反比例函数关系式为: y2 . -----------------------1分x
将 y -1代入 y 4 可得 x -4,
x
∴n -4; y - ----------------------2 分
把 A(1, 4),B(-4, -1)代入 y1 ax+b, A
得: a b 4,
C
4a b 1.
a 1 D O x∴ b 3 B
∴一次函数关系式为 y1 x+3; ----------------------4分
九年级数学答案 第 2 页 共 6 页
(2)AD BC; -----------------------6分
(3)由图可知:当-4<x<0或x>1时,y1>y2. -----------------------8分
22.解: (1)如图,以点 O为原点,OB所在直线为 x轴建立平面直角坐标系, -----------------------1分
设抛物线解析式为 y=a(x-2)2+0.45,
把 A(0,0.25)代入得:0.25=a(0-2)2+0.45,
解得:a=-0.05.
∴抛物线的表达式为 y=-0.05(x-2)2+0.45; -----------------------4分
(2) 把 y=0代入,得-0.05(x-2)2+0.45=0,
解得:x1=5,x2=﹣1,∴B(5,0),
∴OB=5,
∴喷灌器 OA与围墙的距离 OB为 5m; -----------------------6分
(3) 如图,由题意得:CD=0.4m,BC=0.8m,
∴D(4.2,0.4),E(5,0.4),
设 y=-0.05(x-2)2+k,把 D(4.2,0.4)代入
得,0.4=-0.05(4.2-2)2+k,
解得:k=0.642,∴y=-0.05(x-2)2+0.642,
当 x=0时,y=0.442,∴(OA)min=0.442m, -----------------------8分
设 y=-0.05(x-2)2+k′,把 E(5,0.4)代入得,0.4=-0.05(5-2)2+k′,
解得:k′=0.85,∴y=-0.05(x-2)2+0.85,
当 x=0时,y=-0.05(0-2)2+0.85=0.65,
∴(OA)max=0.65m,
∴0.442m ≤OA ≤0.65m. -----------------------10分
23. 1 = ,理由如下: -----------------------1分
∵△ 是等边三角形,
∴ ∠ = 60°,
∵ ∠ = 30°,∠ = ∠ + ∠ ,
九年级数学答案 第 3 页 共 6 页
∴ ∠ = 60° ∠ = 30°,
∴ ∠ = ∠ ,
∴ = ; -----------------------3分
2 如图 2,取 的中点 ,连接 , , -----------------------4分
∵ ∠ = 90°,∠ = 30°,
∴ ∠ = 60°, = ,
∴△ 为等边三角形.
∴ = .
∵△ 是等边三角形,
∴ = ,∠ = 60° = ∠ .
∴ ∠ = ∠ ,
∴△ ≌△ SAS .
∴ ∠ = ∠ = 60°.
∴ ∠ = 180° 60° 60° = 60°.
∴△ ≌△ SAS . -----------------------6分
∴ = .
∴ = ; -----------------------7分
(3)如图 3,取 的中点 ,连接 , , ,
与(2)同理,△ ≌△ ,△ 是为等边三角形,
∴ ∠ = ∠ = 60°,
∴ ∠ = 60° = ∠ .
又 = , = ,
∴△ ≌△ (SAS) .
∴ = ,
∴ = ,
∵ ⊥ ,
∴ = = 3,
∵ // ,
九年级数学答案 第 4 页 共 6 页
∴ ∠ = 180° ∠ = 120°,
∵ ∠ = ∠ + 60° = ∠ + 60°,
∴ ∠ = ∠ ,
在△ 和△ 中,
∠ = ∠
∠ = ∠ ,
=
∴△ ≌△ (AAS) .
∴ = ,
设 = ,则 = 5 , = ,
∴ = = 4 ,
∵ = ,
∴ 4 = + 3 + 3,
解得, = 2,
∴ = 2. -----------------------11分
24.解:(1) ∵抛物线 y=ax2+2x+c的对称轴为 x=1,与 y轴交于点 C(0,5),
2
∴ 1,解得:a=-1.
2a
又抛物线 y=ax2+2x+c与 y轴交于点 C(0,5),
∴c=5.
∴抛物线的解析式为 y=-x2-2x+5. -----------------------2分
把 y=-x+1代入 y=-x2+2x+5
得 x2-3x-4=0,
解得:x1=-1,x2=4.
∴D(﹣1,2),E(4,﹣3); -----------------------4分
(2)①如图 2,设直线 DE分别交 x轴,y轴于点 L,F,PQ交 y轴于点 H,
过点 G作 GK⊥y轴于点 K,
则 F(0,1),L(1,0),
∴OF=OL=1.
九年级数学答案 第 5 页 共 6 页
∵∠FOL=90°,
∴△FOL是等腰直角三角形.∴∠GFH=45°.
∵四边形 DPEQ是菱形,
3 1
∴DG=EG,PQ⊥DE.∴G( , ).
2 2
1 3
∵GK⊥y轴,∴K(0, ).∴FK=GK= .
2 2
∵∠FGH=90°,∴△FGH是等腰直角三角形.
∴FH=2FK=3,
∴H(0,﹣2).∴直线 GH的解析式为 y=x-2.
把 y=x-2代入 y=-x2+2x+5得 x2-3x-4=0,
x
1 29
1 x
1 29
2
解得: 2 (舍去), 2 ,
y 3 29 y 3 29 1 2 2 2
1 29 -3 29
∴点 P的坐标为( , ); -----------------------8分
2 2
②如图 3,设直线 DE交 y轴于点 F,过点 P作 PJ∥y轴交 DE于 J,
设 P(t,-t2+2t+5),则 J(t,-t+1),
∴PJ=-t2+2t+5-(-t+1)=-t2+3t+4.
由①知∠GFH=45°.
∵PJ∥y轴,
∴∠PJG=∠GFH=45°.
∵P,Q关于直线 DE对称,
∴PQ⊥DE,即∠PGJ=90°,PQ=2PG.
∴△PJG是等腰直角三角形.
∴PG= 2 PJ.
2
∴PQ=2PG= 2 PJ= 2(﹣t2+3t+4)=- 2(t- 3)2+ 25 2 .
2 4
∵ 2<0,
∴当 t= 3 时,线段 PQ的最大值为 25 2 . -----------------------12分
2 4
九年级数学答案 第 6 页 共 6 页
九年级数学试题
(本试题共 6页,满分 120分,考试时间 120分钟)
注意事项:
1、答题前,考生务必将姓名、准考证号填写在答题卡上;并将“条形码”粘贴在答题卡指
定位置。
2、每道选择题的答案选出后,请用 2B铅笔把答题卡上对应的答案标号涂黑。如需改动,
先用橡皮擦干净后,再选涂其他答案标号。非选择题的答案也应写在答题卡对应的区域内,
写在试卷上无效。
3、考试结束,请将本试卷和答题卡一并上交。
一、选择题(本大题共 10个小题,每小题 3分,满分 30分)
1.2025年 1月 5日,是二十四节气的小寒.二十四节气是中国劳动人民独创的文化遗产,能
反映季节的变化,指导农事活动.下面四幅图片分别代表“立夏”、“大雪”、“小寒”、“立
春”,其中是中心对称图形的是
A B C D
2.若方程 x2-(k-1)x+2=0有一个根是 x=-1,则 k的值是
A.-2 B.-1 C.1 D.2
3.下列事件中是必然事件的是
A.床前明月光 B.大漠孤烟直 C.黄河入海流 D.手可摘星辰
4.关于二次函数 y=(x+2)2+6的图象,下列结论正确的是
A.开口向下 B.对称轴是 x=2
C.与 y轴交于点(0,6) D.当 x<-2时,y随 x的增大而减小
5.设 a,b是方程 x2+x-2024=0的两个实数根,则 a2+2a+b的值为
A.2022 B.2023 C.2024 D.2025
6.汽车刹车后行驶的距离 S(单位:米)关于行驶时间 t(单位:秒)的函数关系式是 S=6t
-t2,则该汽车从刹车到停止所用时间为
A.3秒 B.6秒 C.9秒 D.10秒
7.用半径为 30,圆心角为 120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面半径是
A.20 B.15 C.10 D.5
九年级数学试卷 第 1 页 (共 6 页)
8 k.如图,点 P是反比例函数 y (k≠0)的图象上任意一点,过点 P作 PM⊥x轴,垂足为
x
M,若△POM的面积等于 4,则 k的值等于
A.8 B.4 C.-4 D.-8
9.如图,△ABC内接于⊙O,连接 OA,OB.若 OA=4,∠C=45°,则图中阴影部分的面积为
A.π-2 B. 4π-4 C. 4π-8 D. 4π-4 2
(第 8题) (第 9题) (第 10题)
10. 如图,点 O是等边△ABC内一点,OA=4,OB=2,OC=2 3,则△ABC的面积是
A.8 3 B.7 3 C.4 3 D.3 3
二、填空题(本大题共 5个小题,每小题 3分,满分 15分)
11. 在平面直角坐标系中,点 P(-4,5)关于原点的对称点 P ′ 的坐标是 .
12. 三阶幻方,起源于中国,是古代劳动人民智慧的结晶.它是由 9 个数组成的一个 3×3
的方格,且每一横行,每一竖列以及两条对角线上的三个数的和都相等.如图,是一个
残缺的幻方,根据图中已知的 3个数,可得 x= .
6
x
5 10
(第 12题) (第 13题) (第 15题)
13. 如图,已知正方形二维码的边长为 3 cm,为了测算黑色部分的面积,在正方形区域内随
机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在 0.6左右,由此可估计这
个正方形二维码图中的黑色部分的面积约为 cm2.
九年级数学试卷 第 2 页 (共 6 页)
14. 我国南宋数学家杨辉在《田亩比类乘除算法》中记录了这样一个问题:“直田积八百六
十四步,只云阔与长共六十步,问阔及长各几步?”其大意是:矩形面积是 864平步,
其中宽与长的和为 60 步,问宽和长各几步?若设矩形的长为 x 步,根据题意可列方
程 .
15. 抛物线 y=ax2+bx+c的顶点为 A(2,m),且经过点 B(5,0),其部分图象如图所示.对
于此抛物线有如下四个结论:①abc<0;②a-b+c<0;③4a+b=0;④若此抛物线经过
点 C(-2,n),则不等式 ax2+bx+c-n<0的解集是-2<x<6.其中所有正确结论的序
号是 .
三、解答题(本大题共 9个小题,满分 75分)
16.(6分)
解方程:(1)x2-6x-7=0; (2)x(x-2)=3x-6.
17.(6分)
某校开展数学趣味知识竞赛活动,要求参赛学生从 “A:幻方; B:数独; C :魔方”
三个项目中选择 1~2个项目参加比赛.现将“A ”“ B ”“ C ”分别写在 3张无差别
的不透明的卡片正面上,洗匀后正面向下放在桌面上,等候参赛选手随机抽取.
(1)小明同学选择一项参赛,他随机抽取一张卡片,恰好选中项目“A ”是
事件;(填“确定”或“随机”)
(2)小亮同学选择两项参赛,他随机一次性抽取两张卡片,求都没有抽到项目“ B ”的
概率.
18.(6分)
如图,正方形网格中,每个小正方形的边长都是一个单
位长度,在平面直角坐标系中,△ABC的三个顶点坐标
A(-2,0),B(-5,-3),C(0,-5)都在格点上.
(1)若△ABC 平移后得到△A1B1C1,当 A1 的坐标为
(4,4),画出△A1B1C1,并写出 B1,C1的坐标;
(2)将△A1B1C1绕原点逆时针旋转 90°得到△A2B2C2,
画出△A2B2C2,并直接写出点 A2的坐标;
(3)求△A2B2C2的面积.
九年级数学试卷 第 3 页 (共 6 页)
19.(8分)
已知关于 x的一元二次方程 x2+(2m+1)x+m2-1=0有两个不相等的实数根.
(1)求 m的取值范围;
(2)设 x1,x2是方程的两个根且 x12+x22+x1x2-6=0,求 m的值.
20.(8分)
如图,PA切⊙O于点 A,AB是⊙O直径,C是⊙O上一点,PA PC AB,连接 PO交 AC
于点 D.
(1)求证:PC是⊙O的切线; A
(2)若 BC 2,求 AB的长.
P D O
C B
21.(8分)
如图,已知一次函数 y1
m
ax+b与反比例函数 y2 x 的图象在第一,第三象限分别交于
A(1,4), B(n, -1)两点,直线 AB与 y轴,x轴分别交于 C,D两点.
(1)求一次函数和反比例函数关系式; y
(2)比较大小: AD BC(填“<”,“ ”或“>” );
(3)当 y1>y2时,请直接写出 x的取值范围. A
C
D O x
B
九年级数学试卷 第 4 页 (共 6 页)
22.(10分)
根据以下素材,探索完成任务.
如何设计喷灌器喷水口的升降方案
随着自动化设备的普及,家庭庭院也引
入自动喷灌系统.图 1中某庭院内有一
个可垂直升降的草坪喷灌器,从喷水口
素 喷出的水柱成抛物线形.图 2是该喷灌
材 器 OA喷水时的截面示意图,喷水口 A
1 点离地高度 AO=0.25m,喷出的水柱在
离喷水口水平距离为 2m处达到最高,
高度为 0.45m,且水柱刚好落在庭院围
墙和地面的交界 B点处.
为了美化庭院,准备在庭院内沿围墙建
花坛种花,花坛高 DC =0.4m,宽 BC=DE
=0.8m,侧面用大理石包围,矩形 BCDE
素
是花坛截面,如图 3.调整喷水口的高
材
2 度,喷出的水柱形状与原来相同且随之
上下平移,使花坛的上方从 D到 E的区
域刚好都能被水柱浇灌(大理石厚度不
计),从而达到给花坛喷灌的效果.
解决问题
在图 2中,建立合适的平面直角坐标系,求
任务 1 确定水柱的形状
抛物线的解析式?
任务 2 确定喷灌器的位置 求喷灌器OA与围墙的水平距离OB是多少?
调整喷水口的高度,使花坛的上方 DE边上
任务 3 拟定喷头升降方案 刚好都能被水柱喷灌,请直接写出喷水口距
离地面高度的取值范围.
九年级数学试卷 第 5 页 (共 6 页)
23.(11分)
【问题提出】
在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点 D在边 AB上,探究
ED与 EB数量关系.
【问题探究】
(1)如图 1,当点 E在边 BC上时,猜想 ED与 EB数量关系,并加以证明;
(2)如图 2,当点 E在△ABC内部时,证明(1)中的结论仍然成立;
【问题拓展】
(3)如图 3,当点 E在△ABC外部时,EF⊥AB于点 F,过点 E作 EG∥AB,交线段 AC
的延长线于点 G,AG=5CG,BF=3,请直接写出 CG的长.
C G EC C
E
E
A D B A D B
图 1 2 A D F B图 图 3
24.(12分)
如图所示,抛物线 y=ax2+2x+c的对称轴为 x=1,与 x轴交于 A,B两点,与 y轴交于
点 C(0,5),直线 y=-x+1与该抛物线交于 D,E两点(点 D在点 E的左侧).
(1)求该抛物线的解析式及 D,E两点的坐标;
(2)如图 2,将位于直线 DE上方的抛物线沿着直线 DE翻折,点 P是 DE上方的抛物
线上的一动点,点 P的对应点为点 Q,连接 PQ交 DE于点 G.
①当四边形 DPEQ是菱形时,请直接写出点 P的坐标;
②在点 P的运动过程中,请求出线段 PQ的最大值.
图 1 图 2
九年级数学试卷 第 6 页 (共 6 页)
仙桃市 2024 年秋季学期期末质量监测
九年级数学考答案及评分说明
说明:本评分说明一般只给出一种解法,对其他解法,只要推理严谨,运算合理,结果正确,均给满分;
对部分正确的,参照此评分说明,酌情给分.
一、选择题(每小题 3 分,满分 30 分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C D B A C D C B
二、填空题(每小题 3 分,共 15 分)
11.(4,-5); 12.9; 13.5.4 ;
14.x(60- x)=864; 15.①③.(每填对 1个得 2分,填对 2个得 3分)
三、解答题(共 75 分)
16.解:(1)x1=-1,x2=7; -----------------------3分
(2)x1=2,x2=3. -----------------------6分
17.解:(1)随机; -----------------------2分
1
(2)P(都没有抽到项目“B”)= . -----------------------6 分3
18.解:(1)如图所示,△A1B1C1即为所求,B1(1,1)C1(6,-1); -----------------------2 分
(2)如图所示,△A2B2C2即为所求,点 A2(-4,4); -----------------------4分
(3)S△A2B2C2=S△ABC=10.5. -----------------------6 分
5
19.解:(1)m的取值范围是 m> ; -----------------------4分
4
2
(2)m= . -----------------------8分
3
九年级数学答案 第 1 页 共 6 页
A
20.(1)证明:如图,连接 OC,
∵ PA是⊙O的切线,
P D O
∴PA⊥OA .
∴∠PAO 90° .
C B
∵ OC OA,PC PA,OP OP.
∴△POC≌△POA(SSS). -----------------------2分
∴ ∠PCO ∠PAO 90° .
∴ OD⊥CD .
又点 C在⊙O上,
∴ PC是⊙O的切线; -----------------------4分
(2) 解: 如图,由(1)可证:
∠PDA ∠ACB 90°,∠APD ∠BAC.
又 PA AB,
∴△PAD≌△ABC(AAS). -----------------------6分
∴ AD BC 2,AC 2AD 4.
在 Rt△ABC中,由勾股定理可得:
AB 22 42 2 5. -----------------------8分
m
21. 解:(1)将 A(1, 4)代入 y (m为常数,m 0)x 可得:m 4.
4
∴反比例函数关系式为: y2 . -----------------------1分x
将 y -1代入 y 4 可得 x -4,
x
∴n -4; y - ----------------------2 分
把 A(1, 4),B(-4, -1)代入 y1 ax+b, A
得: a b 4,
C
4a b 1.
a 1 D O x∴ b 3 B
∴一次函数关系式为 y1 x+3; ----------------------4分
九年级数学答案 第 2 页 共 6 页
(2)AD BC; -----------------------6分
(3)由图可知:当-4<x<0或x>1时,y1>y2. -----------------------8分
22.解: (1)如图,以点 O为原点,OB所在直线为 x轴建立平面直角坐标系, -----------------------1分
设抛物线解析式为 y=a(x-2)2+0.45,
把 A(0,0.25)代入得:0.25=a(0-2)2+0.45,
解得:a=-0.05.
∴抛物线的表达式为 y=-0.05(x-2)2+0.45; -----------------------4分
(2) 把 y=0代入,得-0.05(x-2)2+0.45=0,
解得:x1=5,x2=﹣1,∴B(5,0),
∴OB=5,
∴喷灌器 OA与围墙的距离 OB为 5m; -----------------------6分
(3) 如图,由题意得:CD=0.4m,BC=0.8m,
∴D(4.2,0.4),E(5,0.4),
设 y=-0.05(x-2)2+k,把 D(4.2,0.4)代入
得,0.4=-0.05(4.2-2)2+k,
解得:k=0.642,∴y=-0.05(x-2)2+0.642,
当 x=0时,y=0.442,∴(OA)min=0.442m, -----------------------8分
设 y=-0.05(x-2)2+k′,把 E(5,0.4)代入得,0.4=-0.05(5-2)2+k′,
解得:k′=0.85,∴y=-0.05(x-2)2+0.85,
当 x=0时,y=-0.05(0-2)2+0.85=0.65,
∴(OA)max=0.65m,
∴0.442m ≤OA ≤0.65m. -----------------------10分
23. 1 = ,理由如下: -----------------------1分
∵△ 是等边三角形,
∴ ∠ = 60°,
∵ ∠ = 30°,∠ = ∠ + ∠ ,
九年级数学答案 第 3 页 共 6 页
∴ ∠ = 60° ∠ = 30°,
∴ ∠ = ∠ ,
∴ = ; -----------------------3分
2 如图 2,取 的中点 ,连接 , , -----------------------4分
∵ ∠ = 90°,∠ = 30°,
∴ ∠ = 60°, = ,
∴△ 为等边三角形.
∴ = .
∵△ 是等边三角形,
∴ = ,∠ = 60° = ∠ .
∴ ∠ = ∠ ,
∴△ ≌△ SAS .
∴ ∠ = ∠ = 60°.
∴ ∠ = 180° 60° 60° = 60°.
∴△ ≌△ SAS . -----------------------6分
∴ = .
∴ = ; -----------------------7分
(3)如图 3,取 的中点 ,连接 , , ,
与(2)同理,△ ≌△ ,△ 是为等边三角形,
∴ ∠ = ∠ = 60°,
∴ ∠ = 60° = ∠ .
又 = , = ,
∴△ ≌△ (SAS) .
∴ = ,
∴ = ,
∵ ⊥ ,
∴ = = 3,
∵ // ,
九年级数学答案 第 4 页 共 6 页
∴ ∠ = 180° ∠ = 120°,
∵ ∠ = ∠ + 60° = ∠ + 60°,
∴ ∠ = ∠ ,
在△ 和△ 中,
∠ = ∠
∠ = ∠ ,
=
∴△ ≌△ (AAS) .
∴ = ,
设 = ,则 = 5 , = ,
∴ = = 4 ,
∵ = ,
∴ 4 = + 3 + 3,
解得, = 2,
∴ = 2. -----------------------11分
24.解:(1) ∵抛物线 y=ax2+2x+c的对称轴为 x=1,与 y轴交于点 C(0,5),
2
∴ 1,解得:a=-1.
2a
又抛物线 y=ax2+2x+c与 y轴交于点 C(0,5),
∴c=5.
∴抛物线的解析式为 y=-x2-2x+5. -----------------------2分
把 y=-x+1代入 y=-x2+2x+5
得 x2-3x-4=0,
解得:x1=-1,x2=4.
∴D(﹣1,2),E(4,﹣3); -----------------------4分
(2)①如图 2,设直线 DE分别交 x轴,y轴于点 L,F,PQ交 y轴于点 H,
过点 G作 GK⊥y轴于点 K,
则 F(0,1),L(1,0),
∴OF=OL=1.
九年级数学答案 第 5 页 共 6 页
∵∠FOL=90°,
∴△FOL是等腰直角三角形.∴∠GFH=45°.
∵四边形 DPEQ是菱形,
3 1
∴DG=EG,PQ⊥DE.∴G( , ).
2 2
1 3
∵GK⊥y轴,∴K(0, ).∴FK=GK= .
2 2
∵∠FGH=90°,∴△FGH是等腰直角三角形.
∴FH=2FK=3,
∴H(0,﹣2).∴直线 GH的解析式为 y=x-2.
把 y=x-2代入 y=-x2+2x+5得 x2-3x-4=0,
x
1 29
1 x
1 29
2
解得: 2 (舍去), 2 ,
y 3 29 y 3 29 1 2 2 2
1 29 -3 29
∴点 P的坐标为( , ); -----------------------8分
2 2
②如图 3,设直线 DE交 y轴于点 F,过点 P作 PJ∥y轴交 DE于 J,
设 P(t,-t2+2t+5),则 J(t,-t+1),
∴PJ=-t2+2t+5-(-t+1)=-t2+3t+4.
由①知∠GFH=45°.
∵PJ∥y轴,
∴∠PJG=∠GFH=45°.
∵P,Q关于直线 DE对称,
∴PQ⊥DE,即∠PGJ=90°,PQ=2PG.
∴△PJG是等腰直角三角形.
∴PG= 2 PJ.
2
∴PQ=2PG= 2 PJ= 2(﹣t2+3t+4)=- 2(t- 3)2+ 25 2 .
2 4
∵ 2<0,
∴当 t= 3 时,线段 PQ的最大值为 25 2 . -----------------------12分
2 4
九年级数学答案 第 6 页 共 6 页
同课章节目录
