7.3.2 正弦型函数的性质与图象(二) 课件(共20张PPT) 2024-2025学年人教B版(2019)高中数学必修第三册
文档属性
| 名称 | 7.3.2 正弦型函数的性质与图象(二) 课件(共20张PPT) 2024-2025学年人教B版(2019)高中数学必修第三册 |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
人教B版(2019)必修第三册
7.3.2 正弦型函数的性质与图象(二)
1.能根据y=Asin(ωx+φ)的部分图象确定其解析式.
2.会求函数y=Asin(ωx+φ)的周期、单调性、最值、对称性.
3.能利用y=Asin(ωx+φ)的性质与图象解决综合问题.
讨论1:函数的定义域、值域、周期是多少?
令,则可以化为.
由的定义域为,值域为,可知
函数的定义域为R,值域为.
由的周期为可知,对任意当它增加到且至少要增加到时,对应的函数值才重复出现 .
因为
即对任意当它增加到且至少要增加到时,的函数值才重复出现 .
所以的周期为π.
讨论1:函数的定义域、值域、周期是多少?
讨论2:函数的对称轴、对称中心、单调区间是什么?
令,则可以化为.
(1)因为的对称轴为,
所以,解得.
所以的对称轴为.
(2)同理,因为的对称中心为,
所以,解得.
所以的对称中心为.
(3)因为的单调增区间为
所以,
解得.
所以的单调增区间为.
同理的单调减区间为.
名称 性质
定义域
值域
周期性
对称中心
对称轴
单调性
y=Asin(ωx+φ)(A>0,ω>0)
R
[-A,A]
T=
练习1:如何求函数的单调增区间?
.
单调性相反
令,.
解得.
所以的单调增区间为.
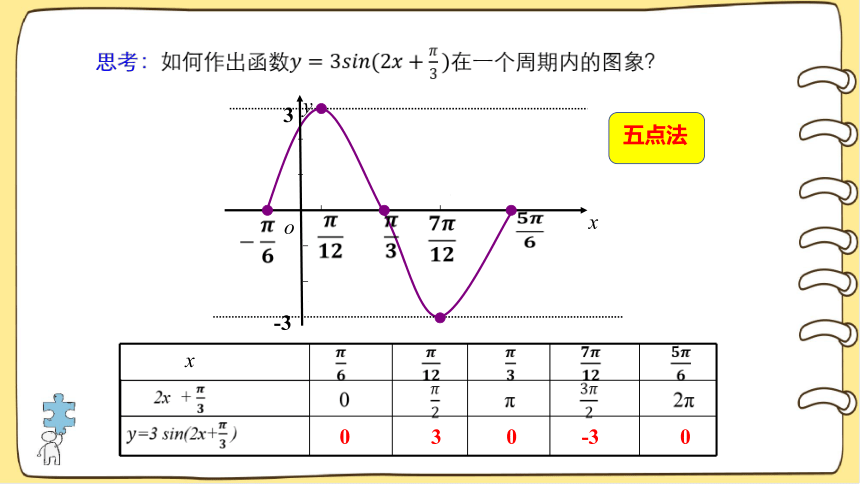
思考:如何作出函数在一个周期内的图象?
-3
3
y
x
0 π 2π
x
o
0 3 0 -3 0
五点法
纵坐标不变
横坐标缩短
到原来1/2
图像向左平移
π/6个单位
横坐标不变
纵坐标伸长
到原来的3倍
x
y=sinx
y=sin2x
y=3sin(2x+)
y=3sin2x
y
o
图像变换法
单个x的变化
先伸缩后平移
向左平移
个单位
纵坐标不变
横坐标缩短到
原来的1/2倍
纵坐标伸长
到原来3倍
x
o
y=sinx
y=sin(x+)
y=sin(2x+)
y=3sin(2x+)
横坐标不变
y
一步到位
图像变换法
先平移后伸缩
由函数y=sin x的图象经变换得到y=Asin(ωx+φ)的图象的步骤:
归纳总结
练习2:将函数y=f(x)图象上每个点的纵坐标保持不变,横坐标伸长到原来的2倍,然后再将整个图象沿x轴向左平移 个单位,得到曲线y= sin x的图象相同,则y=f(x)的函数表达式为( )
D
例1 函数f(x) =Asin(ωx+ )(A>0,ω>0,| |< )的部分图像如图所示,则f(x) = .
根据图像求解析式的方法:
(1)由图像的最高点、最低点确定最值,从而求A.
(2)由图像的零点、最值点确定周期,从而求ω.
(3)由图像上一个点的坐标代入后根据范围求φ.
方法归纳
此时 (k∈Z),
当 (k∈Z)时,f(x)单调递减,
当 (k∈Z)时,f(x)单调递增,
例2 求 的值域和单调区间.
此时 (k∈Z),
综上所述:f(x)的单调递增区间为 (k∈Z),
递减区间为 (k∈Z).
解:令 ,y=f(x),则y=2sin u,∴f(x)的值域为[-2,2],
例3 求 的对称轴和对称中心.
解:令 ,y=f(x),则y=2sin u,
令 (k∈Z)即 (k∈Z),
令 (k∈Z)即 (k∈Z),
∴f(x)的对称中心为 (k∈Z).
∴f(x)的对称轴为 (k∈Z).
1.函数f(x)=sin(x+)的一个单调递减区间是( )
A.[-,] B.[-π,0] C.[-,] D.[,]
2.函数y=Asin(ωx+φ)+k的图象如图所示,则它的振幅A与最小正周期T分别是( )
A.A=3,T= B.A=3,T=
C.A=,T= D.A=,T=
D
D
①②③
3.关于函数f(x)=2sin(3x-),有以下3种说法:
①其最小正周期为;
②图象关于点(,0)对称;
③直线x=-是其一条对称轴.
其中正确说法的序号是________.
正弦型函数 y = Asin(ωx + φ) 图像的变换步骤
y=sin( x+ )
y=sinx
y=sin(x+ )
纵坐标变为原来的A倍
y=Asin( x+ )
向左 >0 (向右 <0)
平移| |个单位
纵坐标不变
横坐标不变
横坐标变为原来的 倍
y=sinx
y=sin x
纵坐标变为原来的A倍
y=Asin( x+ )
向左 >0 (向右 <0)
平移 个单位
纵坐标不变
横坐标不变
横坐标变为原来的 倍
人教B版(2019)必修第三册
7.3.2 正弦型函数的性质与图象(二)
1.能根据y=Asin(ωx+φ)的部分图象确定其解析式.
2.会求函数y=Asin(ωx+φ)的周期、单调性、最值、对称性.
3.能利用y=Asin(ωx+φ)的性质与图象解决综合问题.
讨论1:函数的定义域、值域、周期是多少?
令,则可以化为.
由的定义域为,值域为,可知
函数的定义域为R,值域为.
由的周期为可知,对任意当它增加到且至少要增加到时,对应的函数值才重复出现 .
因为
即对任意当它增加到且至少要增加到时,的函数值才重复出现 .
所以的周期为π.
讨论1:函数的定义域、值域、周期是多少?
讨论2:函数的对称轴、对称中心、单调区间是什么?
令,则可以化为.
(1)因为的对称轴为,
所以,解得.
所以的对称轴为.
(2)同理,因为的对称中心为,
所以,解得.
所以的对称中心为.
(3)因为的单调增区间为
所以,
解得.
所以的单调增区间为.
同理的单调减区间为.
名称 性质
定义域
值域
周期性
对称中心
对称轴
单调性
y=Asin(ωx+φ)(A>0,ω>0)
R
[-A,A]
T=
练习1:如何求函数的单调增区间?
.
单调性相反
令,.
解得.
所以的单调增区间为.
思考:如何作出函数在一个周期内的图象?
-3
3
y
x
0 π 2π
x
o
0 3 0 -3 0
五点法
纵坐标不变
横坐标缩短
到原来1/2
图像向左平移
π/6个单位
横坐标不变
纵坐标伸长
到原来的3倍
x
y=sinx
y=sin2x
y=3sin(2x+)
y=3sin2x
y
o
图像变换法
单个x的变化
先伸缩后平移
向左平移
个单位
纵坐标不变
横坐标缩短到
原来的1/2倍
纵坐标伸长
到原来3倍
x
o
y=sinx
y=sin(x+)
y=sin(2x+)
y=3sin(2x+)
横坐标不变
y
一步到位
图像变换法
先平移后伸缩
由函数y=sin x的图象经变换得到y=Asin(ωx+φ)的图象的步骤:
归纳总结
练习2:将函数y=f(x)图象上每个点的纵坐标保持不变,横坐标伸长到原来的2倍,然后再将整个图象沿x轴向左平移 个单位,得到曲线y= sin x的图象相同,则y=f(x)的函数表达式为( )
D
例1 函数f(x) =Asin(ωx+ )(A>0,ω>0,| |< )的部分图像如图所示,则f(x) = .
根据图像求解析式的方法:
(1)由图像的最高点、最低点确定最值,从而求A.
(2)由图像的零点、最值点确定周期,从而求ω.
(3)由图像上一个点的坐标代入后根据范围求φ.
方法归纳
此时 (k∈Z),
当 (k∈Z)时,f(x)单调递减,
当 (k∈Z)时,f(x)单调递增,
例2 求 的值域和单调区间.
此时 (k∈Z),
综上所述:f(x)的单调递增区间为 (k∈Z),
递减区间为 (k∈Z).
解:令 ,y=f(x),则y=2sin u,∴f(x)的值域为[-2,2],
例3 求 的对称轴和对称中心.
解:令 ,y=f(x),则y=2sin u,
令 (k∈Z)即 (k∈Z),
令 (k∈Z)即 (k∈Z),
∴f(x)的对称中心为 (k∈Z).
∴f(x)的对称轴为 (k∈Z).
1.函数f(x)=sin(x+)的一个单调递减区间是( )
A.[-,] B.[-π,0] C.[-,] D.[,]
2.函数y=Asin(ωx+φ)+k的图象如图所示,则它的振幅A与最小正周期T分别是( )
A.A=3,T= B.A=3,T=
C.A=,T= D.A=,T=
D
D
①②③
3.关于函数f(x)=2sin(3x-),有以下3种说法:
①其最小正周期为;
②图象关于点(,0)对称;
③直线x=-是其一条对称轴.
其中正确说法的序号是________.
正弦型函数 y = Asin(ωx + φ) 图像的变换步骤
y=sin( x+ )
y=sinx
y=sin(x+ )
纵坐标变为原来的A倍
y=Asin( x+ )
向左 >0 (向右 <0)
平移| |个单位
纵坐标不变
横坐标不变
横坐标变为原来的 倍
y=sinx
y=sin x
纵坐标变为原来的A倍
y=Asin( x+ )
向左 >0 (向右 <0)
平移 个单位
纵坐标不变
横坐标不变
横坐标变为原来的 倍
