7.3.3 余弦函数的性质与图象 课件(共18张PPT)2024-2025学年人教B版(2019)高中数学必修第三册
文档属性
| 名称 | 7.3.3 余弦函数的性质与图象 课件(共18张PPT)2024-2025学年人教B版(2019)高中数学必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1001.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
7.3.3 余弦函数的性质与图象
人教B版(2019)必修第三册
1.会用“五点法”“图象变换法”作余弦函数和y=Acos(ωx+φ)的图象.
2.理解余弦函数的性质,会求余弦函数的周期、单调区间及最值.
通过前面的学习,我们了解了正弦函数的图象与性质,那么余弦函数的图象与性质又是怎样的呢?
问题1:类比正弦函数的定义,说说什么是余弦函数?
对于任意一个角 x,都有唯一确定的余弦 cos x 与之对应,因此 y = cos x 是一个函数,一般称为余弦函数.
用余弦线可以直观地表示余弦函数的函数值,
如图, 就是角 x 的余弦线.
O
P
x
1
M
问题2:余弦函数与正弦函数之间有什么联系?
y=cos x=sin(x + )
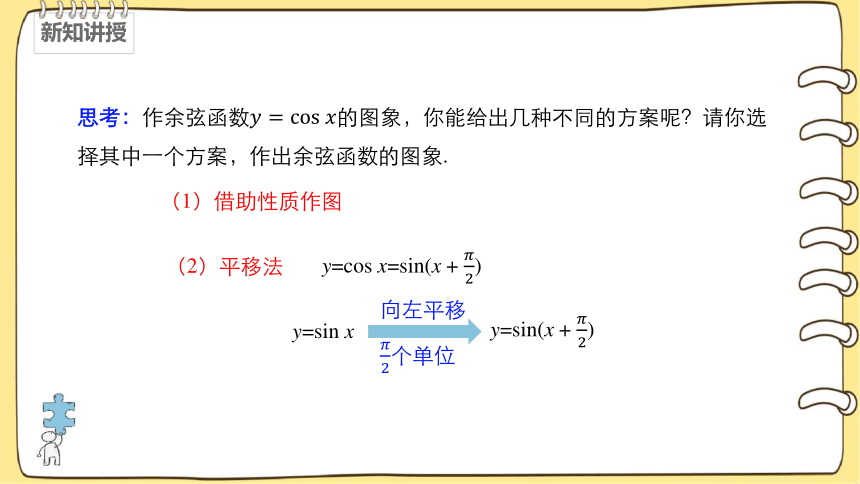
思考:作余弦函数的图象,你能给出几种不同的方案呢?请你选择其中一个方案,作出余弦函数的图象.
(1)借助性质作图
(2)平移法
y=cos x=sin(x + )
y=sin x
y=sin(x + )
向左平移
个单位
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
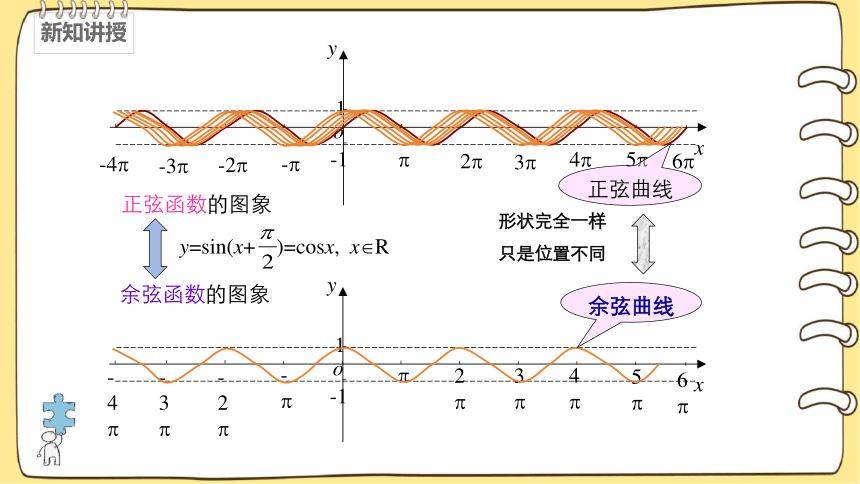
余弦函数的图象
正弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-3
-4
1
-2
y=sin(x+ )=cosx, x R
余弦曲线
正弦曲线
形状完全一样只是位置不同
定义域 零点
值 域 单调性
周 期 对称轴
奇偶性 对称中心
y
x
o
-
-1
2
3
-2
-3
1
R
[-1,1]
时,
时,
由图象记性质,
由性质画图象
偶函数
()
增区间
减区间
()
()
例1 求下列函数的值域:
(1)y=3cos x+1;(2)y=3cos2x-4cos x+1,x∈[,].
解:(1)∵ – 1 ≤ cos x ≤ 1,∴ -3 ≤cos x ≤ 3,且 – 2 ≤ 3cos x + 1 ≤ 4,
即 – 2 ≤ y ≤ 4.
当 cos x = -1 时,ymin= –2;当 cos x = 1 时,ymax= 4;
因此 y =3cos x + 1 的值域为 [–2,4]
(2)y=3cos2x-4cos x+1,x∈[,].
(2)y=3cos2x-4cos x+1=3(cos2x-cos x+)=3(cos x-)2-,
令cos x=t,则y=3(t-)2-,t∈[-1,1],
∵-1≤ t≤1]时,-≤t-≤,
∴0≤(t-)2≤,
∴-≤3(t-)2-≤8,
∴该函数的值域为[-,8].
例2 函数y=3cos 2x+4(x∈R)是( )
A.最小正周期为π的偶函数 B.最小正周期为2π的偶函数
C.最小正周期为π的奇函数 D.最小正周期为2π的奇函数
解析:∵f(x)=3cos 2x+4,x∈R,
∴f(-x)=3cos(-2x)+4=f(x)为偶函数,T==π.
A
判断三角函数的奇偶性的方法:
方法归纳
(1)利用图象法:若图象关于原点对称,则函数为奇函数;
若图象关于y轴对称,则函数为偶函数.
(2)根据奇偶性的定义判断:
若对定义域内的任意x都有f(-x)=f(x),则函数为偶函数;
若对定义域内的任意x都有f(-x)=-f(x),则函数为奇函数.
例3 求函数 y = 2cos ( – ) 的周期和其图象的对称轴方程.
解:因为 y = 2cos ( – ) = 2sin [( – ) + ] = 2sin ( + ),所以 T = = 6π.
令 + = + kπ (k∈Z),解得 x = + 3kπ (k∈Z).
所以函数 y = 2cos ( – ) 的周期为 6π,
其图象的对称轴方程为 x = + 3kπ (k∈Z).
例4 已知函数 f(x) = 2cos(–3x) ,x∈[-,],求f(x)的单调递增区间.
解: f(x)= 2cos(–3x)可化为f(x)=2cos(3x-),
故单调递增区间满足2kπ-π≤3x-≤2kπ,k∈Z,
解得kπ-≤x≤kπ+,k∈Z,
令k=0,-≤x≤,
令k=1,≤x≤,
∵x∈[-,],∴ f(x)的单调递增区间是[-,],[,].
余弦型函数单调区间的求法
①如果x的系数为负,则利用诱导公式变为正.
②将ωx+φ看作整体,代入到余弦函数的单调区间解出x的范围.
③若求具体的或一个范围内的单调区间,则给k赋值,即可求出符合条件的单调区间.
方法归纳
1.下列函数中,周期为 的是( )
2.函数 是( )
A. 奇函数 B. 偶函数
C. 非奇非偶函数 D. 既是奇函数又是偶函数
D
B
3.若a=sin 47°,b=cos 37°,c=cos 47°,则a,b,c大小关系为( )
A.a>b>c B.b>c>a C.b>a>c D.c>b>a
4.函数 f(x) = 2cos(πx-)的图象的对称轴方程为( )
C
C
余弦函数y=cos x的性质与图象小结:
定义域 R
值 域 [-1,1]
奇偶性 偶函数
周期性 2π
单调性 递增:[– π + 2kπ,2kπ] (k∈Z);递减:[2kπ,π + 2kπ] (k∈Z)
对称轴 x = kπ
对称中心 ( + kπ,0)
7.3.3 余弦函数的性质与图象
人教B版(2019)必修第三册
1.会用“五点法”“图象变换法”作余弦函数和y=Acos(ωx+φ)的图象.
2.理解余弦函数的性质,会求余弦函数的周期、单调区间及最值.
通过前面的学习,我们了解了正弦函数的图象与性质,那么余弦函数的图象与性质又是怎样的呢?
问题1:类比正弦函数的定义,说说什么是余弦函数?
对于任意一个角 x,都有唯一确定的余弦 cos x 与之对应,因此 y = cos x 是一个函数,一般称为余弦函数.
用余弦线可以直观地表示余弦函数的函数值,
如图, 就是角 x 的余弦线.
O
P
x
1
M
问题2:余弦函数与正弦函数之间有什么联系?
y=cos x=sin(x + )
思考:作余弦函数的图象,你能给出几种不同的方案呢?请你选择其中一个方案,作出余弦函数的图象.
(1)借助性质作图
(2)平移法
y=cos x=sin(x + )
y=sin x
y=sin(x + )
向左平移
个单位
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦函数的图象
正弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-3
-4
1
-2
y=sin(x+ )=cosx, x R
余弦曲线
正弦曲线
形状完全一样只是位置不同
定义域 零点
值 域 单调性
周 期 对称轴
奇偶性 对称中心
y
x
o
-
-1
2
3
-2
-3
1
R
[-1,1]
时,
时,
由图象记性质,
由性质画图象
偶函数
()
增区间
减区间
()
()
例1 求下列函数的值域:
(1)y=3cos x+1;(2)y=3cos2x-4cos x+1,x∈[,].
解:(1)∵ – 1 ≤ cos x ≤ 1,∴ -3 ≤cos x ≤ 3,且 – 2 ≤ 3cos x + 1 ≤ 4,
即 – 2 ≤ y ≤ 4.
当 cos x = -1 时,ymin= –2;当 cos x = 1 时,ymax= 4;
因此 y =3cos x + 1 的值域为 [–2,4]
(2)y=3cos2x-4cos x+1,x∈[,].
(2)y=3cos2x-4cos x+1=3(cos2x-cos x+)=3(cos x-)2-,
令cos x=t,则y=3(t-)2-,t∈[-1,1],
∵-1≤ t≤1]时,-≤t-≤,
∴0≤(t-)2≤,
∴-≤3(t-)2-≤8,
∴该函数的值域为[-,8].
例2 函数y=3cos 2x+4(x∈R)是( )
A.最小正周期为π的偶函数 B.最小正周期为2π的偶函数
C.最小正周期为π的奇函数 D.最小正周期为2π的奇函数
解析:∵f(x)=3cos 2x+4,x∈R,
∴f(-x)=3cos(-2x)+4=f(x)为偶函数,T==π.
A
判断三角函数的奇偶性的方法:
方法归纳
(1)利用图象法:若图象关于原点对称,则函数为奇函数;
若图象关于y轴对称,则函数为偶函数.
(2)根据奇偶性的定义判断:
若对定义域内的任意x都有f(-x)=f(x),则函数为偶函数;
若对定义域内的任意x都有f(-x)=-f(x),则函数为奇函数.
例3 求函数 y = 2cos ( – ) 的周期和其图象的对称轴方程.
解:因为 y = 2cos ( – ) = 2sin [( – ) + ] = 2sin ( + ),所以 T = = 6π.
令 + = + kπ (k∈Z),解得 x = + 3kπ (k∈Z).
所以函数 y = 2cos ( – ) 的周期为 6π,
其图象的对称轴方程为 x = + 3kπ (k∈Z).
例4 已知函数 f(x) = 2cos(–3x) ,x∈[-,],求f(x)的单调递增区间.
解: f(x)= 2cos(–3x)可化为f(x)=2cos(3x-),
故单调递增区间满足2kπ-π≤3x-≤2kπ,k∈Z,
解得kπ-≤x≤kπ+,k∈Z,
令k=0,-≤x≤,
令k=1,≤x≤,
∵x∈[-,],∴ f(x)的单调递增区间是[-,],[,].
余弦型函数单调区间的求法
①如果x的系数为负,则利用诱导公式变为正.
②将ωx+φ看作整体,代入到余弦函数的单调区间解出x的范围.
③若求具体的或一个范围内的单调区间,则给k赋值,即可求出符合条件的单调区间.
方法归纳
1.下列函数中,周期为 的是( )
2.函数 是( )
A. 奇函数 B. 偶函数
C. 非奇非偶函数 D. 既是奇函数又是偶函数
D
B
3.若a=sin 47°,b=cos 37°,c=cos 47°,则a,b,c大小关系为( )
A.a>b>c B.b>c>a C.b>a>c D.c>b>a
4.函数 f(x) = 2cos(πx-)的图象的对称轴方程为( )
C
C
余弦函数y=cos x的性质与图象小结:
定义域 R
值 域 [-1,1]
奇偶性 偶函数
周期性 2π
单调性 递增:[– π + 2kπ,2kπ] (k∈Z);递减:[2kπ,π + 2kπ] (k∈Z)
对称轴 x = kπ
对称中心 ( + kπ,0)
