7.3.5 已知三角函数值求角 课件(共18张PPT) 2024-2025学年人教B版(2019)高中数学必修第三册
文档属性
| 名称 | 7.3.5 已知三角函数值求角 课件(共18张PPT) 2024-2025学年人教B版(2019)高中数学必修第三册 |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第七章 三角函数
7.3.5 已知三角函数值求角
人教B版(2019)必修第三册
1.掌握已知三角函数值求角的方法,会用已知的三角函数值求角.
2.牢记一些比较常见的三角函数值及其在区间[– 2π,2π]上对应的角,并会用符号arcsin,arccos,arctan表示角.
知道,那么当时,
探究1:如何求解关于x的方程sin x=a和不等式sin xa)的解集?
法一 利用三角函数线
如图,以射线OP与OP′为终边的角构成sin x=a的解集.
终边在图中阴影部分(不含边界)的角构成sin xa的解集.
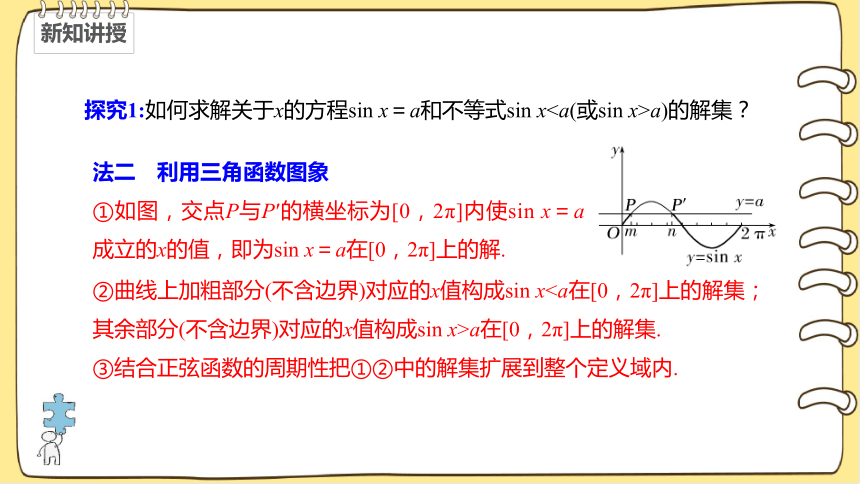
探究1:如何求解关于x的方程sin x=a和不等式sin xa)的解集?
法二 利用三角函数图象
①如图,交点P与P′的横坐标为[0,2π]内使sin x=a成立的x的值,即为sin x=a在[0,2π]上的解.
②曲线上加粗部分(不含边界)对应的x值构成sin xa在[0,2π]上的解集.
③结合正弦函数的周期性把①②中的解集扩展到整个定义域内.
例1 已知sin x=.
(1)当x∈[-]时,求x的取值集合;
(2)当x∈[0,2π]时,求x的取值集合;
(3)当x∈R时,求x的取值集合.
解:(1)∵y=sin x在[-]上是增函数,且sin =,
∴x=,∴{}是所求集合.
(2)∵sin x=>0,∴x为第一或第二象限的角,且sin =sin =,
∴在[0,2π]上符合条件的角有x=或x=π,
∴x的取值集合为{}.
(3)当x∈R时,x的取值集合为{x|x=2kπ+,或x=2kπ+,k∈Z}.
例1 已知sin x=.
(2)当x∈[0,2π]时,求x的取值集合;
(3)当x∈R时,求x的取值集合.
对于已知正弦值求角有如下规律:sin x=a(-1≤a≤1),当x∈R时,可先求得[0,2π]内的所有解α,π-α,再利用周期性可求得:
{x|x=2kπ+α,或x=2kπ+π-α,k∈Z}.
方法归纳
例2 已知cos (2x-)=,求x.
解:由cos (2x-)=>0,知角2x-对应的余弦线方向向右,且长度为,
如图所示,可知角2x-的终边可能是OP,也可能是OP′.
又因为cos =cos (-)=,
所以2x-=-+2kπ或2x-=+2kπ,k∈Z.
所以x=+kπ或x=+kπ,k∈Z.
例3 求不等式cos (x+)>-的解集.
解:如图所示,在[-π,π]上,=-或=时,cos ()=-,
所以=-+2kπ或=+2kπ,
k∈Z时,cos ()=-.
令-+2kπ<<+2kπ,k∈Z,
解得-+4kπ所以不等式的解集为{x|-+4kπ例4 已知tan α=1.
(1)若α∈,求角α;
(2)若α∈R,求角α.
解:(1)由正切函数在开区间上是增函数可知,符合条件tan α=1的角只有一个,即α=.
(2)α=kπ+(k∈Z).
变式:已知tan x=-1,写出在区间[-2π,0]内满足条件的x.
解:∵tan x=-1<0,
∴x是第二或第四象限的角.
由tan =-tan =-1可知,
所求符合条件的第四象限角为x=-.
又由tan (-π)=-tan =-1,得所求符合条件的第二象限角为x=-π,
∴在[-2π,0]内满足条件的角是-与-.
探究2:对于sin x=,cos x=,tan x=2,x∈(0,)对应的角显然不是特殊角,如何表示?
sin x=,则x=arcsin ,
cos x=,则x=arccos ,
tan x=2,则x=arctan 2.
在数学中,任意给定一个 y∈[-1,1],当 sin x = y 且 x∈[,] 时,通常记作 x = arcsin y (反正弦函数);
类似地,在区间 [0,π] 内,满足 cos x = y ( y∈[-1,1] ) 的 x 只有一个,这个 x 记作 arccos y,即 x = arccos y (反余弦函数);
在区间 [,] 内,满足 tan x = y ( y∈R ) 的 x 只有一个,这个 x 记作 arctan y,即 x = arctan y (反正切函数).
例5 计算下列反三角函数的值.
(1)arcsin ; (2)arccos 0; (3)arctan 1.
解:(1)arcsin = ; (2)arccos 0 = ; (3)arctan 1 = .
1.已知cos x=-,π<x<2π,则x=( )
A. B.
C. D.
2.已知α是三角形的内角,且sin α=,则α=( )
A. B.
C.或 D.或
B
D
ABC
3.(多选)以下各式中正确的是( )
4.已知tan 2x=-且x∈[0,π],则x=________.
或
根据今天所学,回答下列问题:
(1)简述由已知的三角函数值求角的方法?
(2)说一说三角函数与反三角函数之间的关系?
第七章 三角函数
7.3.5 已知三角函数值求角
人教B版(2019)必修第三册
1.掌握已知三角函数值求角的方法,会用已知的三角函数值求角.
2.牢记一些比较常见的三角函数值及其在区间[– 2π,2π]上对应的角,并会用符号arcsin,arccos,arctan表示角.
知道,那么当时,
探究1:如何求解关于x的方程sin x=a和不等式sin x
法一 利用三角函数线
如图,以射线OP与OP′为终边的角构成sin x=a的解集.
终边在图中阴影部分(不含边界)的角构成sin x
探究1:如何求解关于x的方程sin x=a和不等式sin x
法二 利用三角函数图象
①如图,交点P与P′的横坐标为[0,2π]内使sin x=a成立的x的值,即为sin x=a在[0,2π]上的解.
②曲线上加粗部分(不含边界)对应的x值构成sin x
③结合正弦函数的周期性把①②中的解集扩展到整个定义域内.
例1 已知sin x=.
(1)当x∈[-]时,求x的取值集合;
(2)当x∈[0,2π]时,求x的取值集合;
(3)当x∈R时,求x的取值集合.
解:(1)∵y=sin x在[-]上是增函数,且sin =,
∴x=,∴{}是所求集合.
(2)∵sin x=>0,∴x为第一或第二象限的角,且sin =sin =,
∴在[0,2π]上符合条件的角有x=或x=π,
∴x的取值集合为{}.
(3)当x∈R时,x的取值集合为{x|x=2kπ+,或x=2kπ+,k∈Z}.
例1 已知sin x=.
(2)当x∈[0,2π]时,求x的取值集合;
(3)当x∈R时,求x的取值集合.
对于已知正弦值求角有如下规律:sin x=a(-1≤a≤1),当x∈R时,可先求得[0,2π]内的所有解α,π-α,再利用周期性可求得:
{x|x=2kπ+α,或x=2kπ+π-α,k∈Z}.
方法归纳
例2 已知cos (2x-)=,求x.
解:由cos (2x-)=>0,知角2x-对应的余弦线方向向右,且长度为,
如图所示,可知角2x-的终边可能是OP,也可能是OP′.
又因为cos =cos (-)=,
所以2x-=-+2kπ或2x-=+2kπ,k∈Z.
所以x=+kπ或x=+kπ,k∈Z.
例3 求不等式cos (x+)>-的解集.
解:如图所示,在[-π,π]上,=-或=时,cos ()=-,
所以=-+2kπ或=+2kπ,
k∈Z时,cos ()=-.
令-+2kπ<<+2kπ,k∈Z,
解得-+4kπ
(1)若α∈,求角α;
(2)若α∈R,求角α.
解:(1)由正切函数在开区间上是增函数可知,符合条件tan α=1的角只有一个,即α=.
(2)α=kπ+(k∈Z).
变式:已知tan x=-1,写出在区间[-2π,0]内满足条件的x.
解:∵tan x=-1<0,
∴x是第二或第四象限的角.
由tan =-tan =-1可知,
所求符合条件的第四象限角为x=-.
又由tan (-π)=-tan =-1,得所求符合条件的第二象限角为x=-π,
∴在[-2π,0]内满足条件的角是-与-.
探究2:对于sin x=,cos x=,tan x=2,x∈(0,)对应的角显然不是特殊角,如何表示?
sin x=,则x=arcsin ,
cos x=,则x=arccos ,
tan x=2,则x=arctan 2.
在数学中,任意给定一个 y∈[-1,1],当 sin x = y 且 x∈[,] 时,通常记作 x = arcsin y (反正弦函数);
类似地,在区间 [0,π] 内,满足 cos x = y ( y∈[-1,1] ) 的 x 只有一个,这个 x 记作 arccos y,即 x = arccos y (反余弦函数);
在区间 [,] 内,满足 tan x = y ( y∈R ) 的 x 只有一个,这个 x 记作 arctan y,即 x = arctan y (反正切函数).
例5 计算下列反三角函数的值.
(1)arcsin ; (2)arccos 0; (3)arctan 1.
解:(1)arcsin = ; (2)arccos 0 = ; (3)arctan 1 = .
1.已知cos x=-,π<x<2π,则x=( )
A. B.
C. D.
2.已知α是三角形的内角,且sin α=,则α=( )
A. B.
C.或 D.或
B
D
ABC
3.(多选)以下各式中正确的是( )
4.已知tan 2x=-且x∈[0,π],则x=________.
或
根据今天所学,回答下列问题:
(1)简述由已知的三角函数值求角的方法?
(2)说一说三角函数与反三角函数之间的关系?
