2025年数学寒假知识巩固第11章三角形(含解析)
文档属性
| 名称 | 2025年数学寒假知识巩固第11章三角形(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 815.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 20:48:25 | ||
图片预览

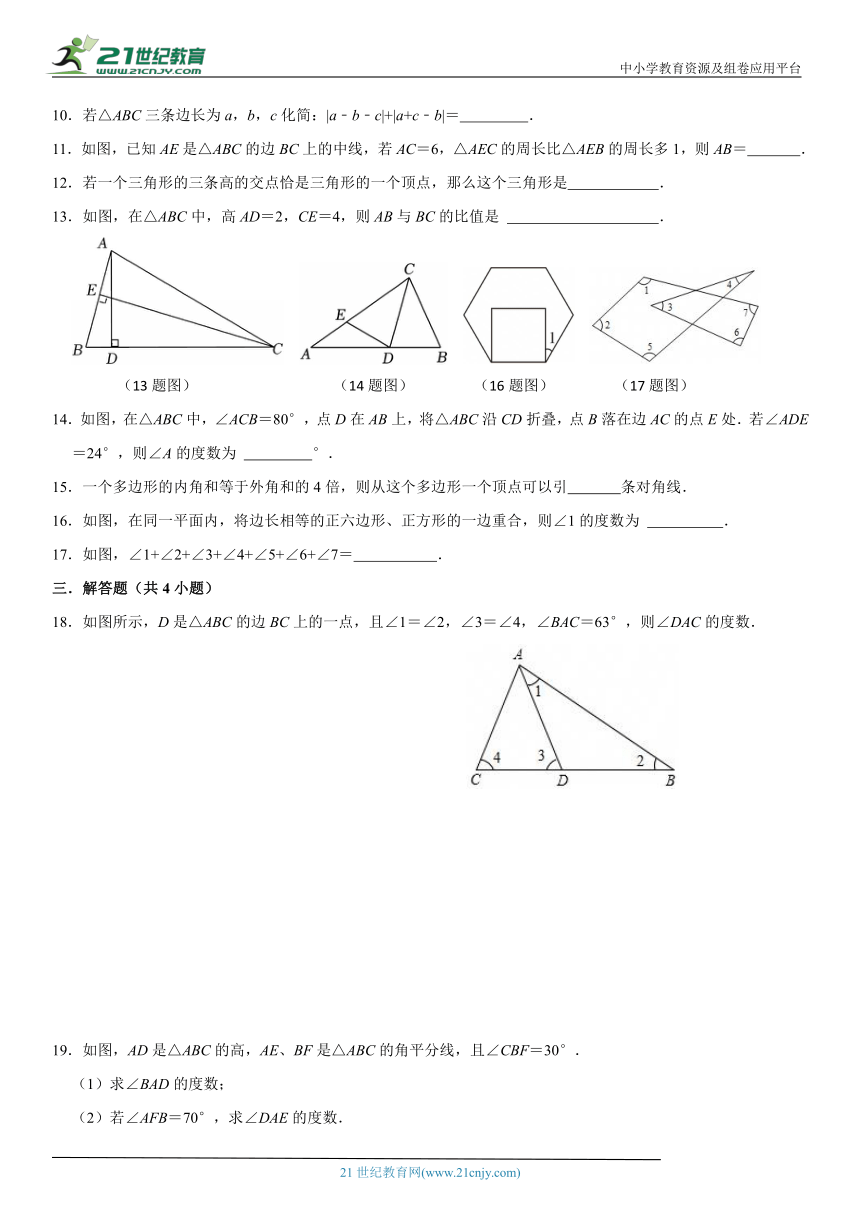

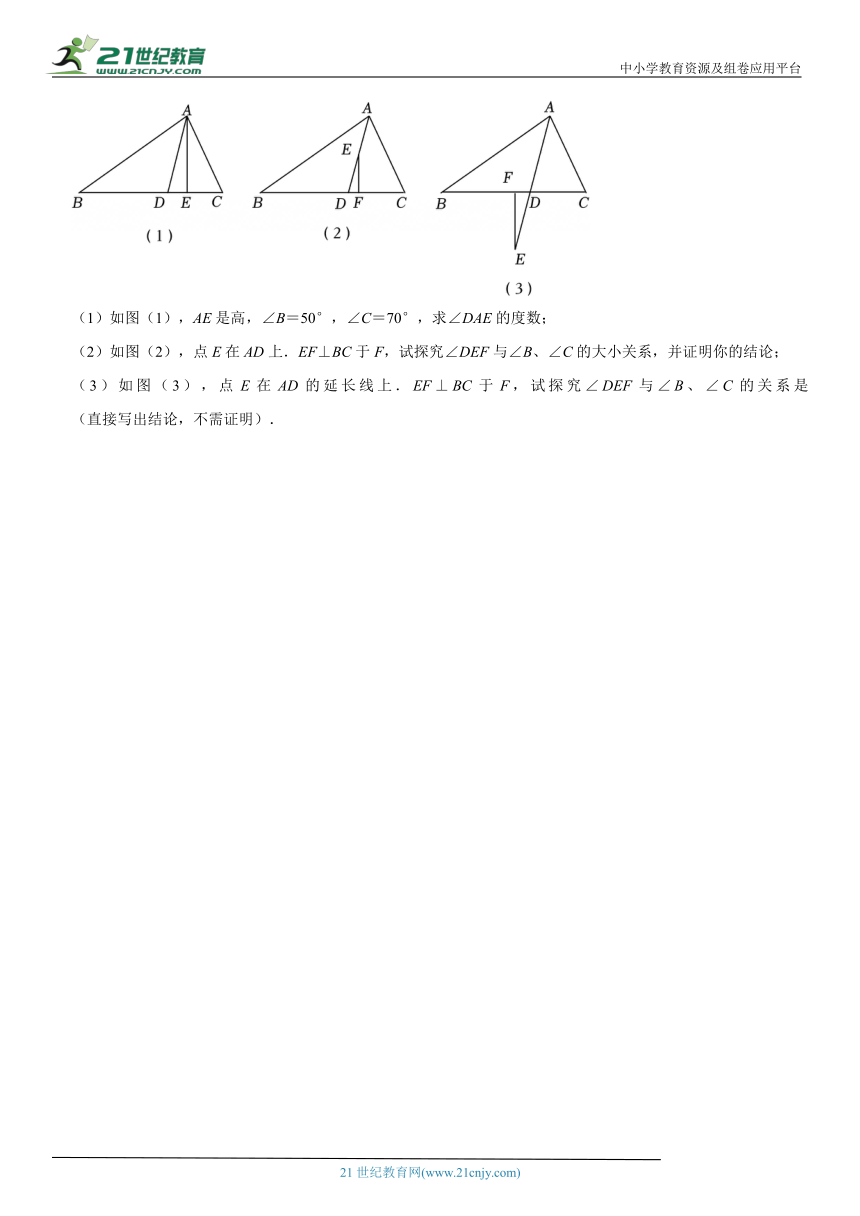

文档简介
中小学教育资源及组卷应用平台
2025年数学寒假知识巩固练习题第11章三角形
复习范围:第11章三角形;考试时间:60分钟;
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共9小题)
1.以下列数值为长度的各组线段中,能组成三角形的是( )
A.2,4,7 B.3,3,6 C.5,8,2 D.4,5,6
2.如图,要使五边形木架(用5根木条钉成)不变形,至少再钉木条的根数为( )
A.5根 B.4根 C.3根 D.2根
3.嘉嘉家、琪琪家和学校不在同一直线上,嘉嘉家和琪琪家到学校的直线距离分别是2km和3km他们两家的直线距离可能是( )
A.1km B.4km C.5km D.6km
4.如图表示三角形的分类,则A表示的是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.三边都不相等的三角形
5.如图,在△ABC中,边AB上的高是( )
A.线段AF B.线段BE C.线段CE D.线段BD
(5题图) (6题图) (7题图) (8题图) (9题图)
6.点O是△ABC内一点,OA、OC分别平分∠BAC、∠BCA,∠B=64°,则∠O=( )
A.116° B.122° C.136° D.152°
7.如图是由一副常规直角三角板摆放得到的图形,图中的∠ABF的度数为( )
A.30° B.15° C.60° D.25°.
8.如图CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,求∠BAC与∠B,∠E的关系是( )
A.∠BAC=∠B+∠E B.∠BAC=∠B+2∠E C.∠BAC=2∠B+∠E D.
9.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是( )
A.∠1+∠2=90° B.∠1+∠4=90° C.∠2+∠4=90° D.∠2=∠3
二.填空题(共8小题)
10.若△ABC三条边长为a,b,c化简:|a﹣b﹣c|+|a+c﹣b|= .
11.如图,已知AE是△ABC的边BC上的中线,若AC=6,△AEC的周长比△AEB的周长多1,则AB= .
12.若一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是 .
13.如图,在△ABC中,高AD=2,CE=4,则AB与BC的比值是 .
(13题图) (14题图) (16题图) (17题图)
14.如图,在△ABC中,∠ACB=80°,点D在AB上,将△ABC沿CD折叠,点B落在边AC的点E处.若∠ADE=24°,则∠A的度数为 °.
15.一个多边形的内角和等于外角和的4倍,则从这个多边形一个顶点可以引 条对角线.
16.如图,在同一平面内,将边长相等的正六边形、正方形的一边重合,则∠1的度数为 .
17.如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7= .
三.解答题(共4小题)
18.如图所示,D是△ABC的边BC上的一点,且∠1=∠2,∠3=∠4,∠BAC=63°,则∠DAC的度数.
19.如图,AD是△ABC的高,AE、BF是△ABC的角平分线,且∠CBF=30°.
(1)求∠BAD的度数;
(2)若∠AFB=70°,求∠DAE的度数.
20.如图,在△ABC中,∠A=35°,∠ABD=35°,∠ACB=80°,且CE平分∠ACB,求∠BEC的度数.
21.在△ABC中,AD是角平分线,∠B<∠C,
(1)如图(1),AE是高,∠B=50°,∠C=70°,求∠DAE的度数;
(2)如图(2),点E在AD上.EF⊥BC于F,试探究∠DEF与∠B、∠C的大小关系,并证明你的结论;
(3)如图(3),点E在AD的延长线上.EF⊥BC于F,试探究∠DEF与∠B、∠C的关系是 (直接写出结论,不需证明).
参考答案
一.选择题(共9小题)
1.解:A、4+2=6<7,不能组成三角形;
B、3+3=6,不能组成三角形;
C、5+2=7<8,不能组成三角形;
D、4+5=9>6,能组成三角形.
选:D.
2.解:如图所示,由三角形具有稳定性可知:要使五边形木架不变形,至少再钉2根木条,
选:D.
3.解:依题意有,设嘉嘉家和琪琪家的直线距离为d km,
则3﹣2≤d≤3+2,
即1≤d≤5.
选:B.
4.解:∵三角形按边分为三边都不等的三角形,等腰三角形,
∴A表示三边都不等的三角形.
选:D.
5.解:根据三角形的高的定义可知:线段CE是边AB边上的高,
选:C.
6.解:在△ABC中,∠B=64°,
∴∠BAC+∠BCA=180°﹣∠B=180°﹣64°=116°.
∵OA、OC分别平分∠BAC、∠BCA,
∴∠OAC∠BAC,∠OCA∠BCA,
∴∠OAC+∠OCA∠BAC∠BCA(∠BAC+∠BCA)116°=58°.
在△OAC中,∠OAC+∠OCA=58°,
∴∠O=180°﹣(∠OAC+∠OCA)=180°﹣58°=122°.
选:B.
7.解:由题意得:∠DAE=45°,
∵∠F=30°,∠DAE是△ABF的外角,
∴∠ABF=∠DAE﹣∠F=45°﹣30°=15°.
选:B.
8.解:∠BAC=∠B+2∠E,
理由:
∵CE是△ABC的外角∠ACD的平分线,
∴∠ACE=∠ECD,
∵∠BAC=∠ACE+∠E,
∠ECD=∠ACE=∠B+∠E,
∴∠BAC=∠B+∠E+∠E=∠B+2∠E.
选:B.
9.解:Rt△ABC中,
∵∠ACB=90°,
∴∠1+∠2=90°,A正确;
∵CD⊥AB,
∴∠ADC=90°,
∴∠1+∠3=90°,
∴∠2=∠3,D正确;
∵∠3+∠4=90°,
∴∠1=∠4,B不正确;
∵∠2+∠4=90°,C正确;
选:B.
二.填空题(共8小题)
10.解:a﹣b<c,a+c>b,
|a﹣b﹣c|+|a+c﹣b|
=c﹣(a﹣b)+a+c﹣b
=2c.
答案为:2c.
11.解:∵AE是△ABC的边BC上的中线,
∴CE=BE,
∵△ACE的周长比△AEB的周长多1,
∴(AC+AE+CE)﹣(AB+BE+AE)=1,即AC﹣AB=1,
∵AC=6,
∴AB=5,
答案为:5.
12.解:因为直角三角形的直角所在的顶点正好是三条高线的交点,所以可以得出这个三角形是直角三角形.
答案为:直角三角形.
13.解:S△ABCAB CEBC AD,
∴4AB=2BC,
∴,
答案为:.
14.解:在△ABC中,∠ACB=80°,
∴∠B=180°﹣∠A﹣∠ACB
=100°﹣∠A,
∵将△ABC沿CD折叠,点B落在边AC的点E处,
∴∠CED=∠B=100°﹣∠A,
∵∠CED是△ADE的一个外角,∠ADE=24°,
∴∠CED=∠A+∠ADE,
即,100°﹣∠A=∠A+24°
解得:∠A=38°.
答案为:38.
15.解:设这个正多边形的边数是n,则
(n﹣2) 180°=1440°,
解得:n=10.
则从这个多边形一个顶点可以引7条对角线.
16.解:正六边形的一个内角的度数为,正方形的一个内角的度数为90°,
由图可知:∠1=120°﹣90°=30°;
答案为:30°.
17.解:如图,
∵∠3+∠4+8=180°①,
∠6+∠7+∠10+∠11=360°②,
∠1+∠2+∠5+∠9=360°③,
∴①+②+③得,∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠9+∠10+∠11+∠12=900°,
∵∠8+∠10=180°,∠9+∠11=180°,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7
=900°﹣180°﹣180°
=540°.
答案为:540°.
三.解答题(共4小题)
18.解:∵∠3=∠1+∠2,∠1=∠2,∠3=∠4,
∴∠4=2∠2.
∵∠2+∠4+∠BAC=180°,∠BAC=63°,
∴3∠2+63°=180°,
∴∠2=39°,
∴∠1=∠2=39°,
∴∠DAC=63°﹣39°=24°.
19.解:(1)由题意可知:∠ABC=2∠CBF=60°,
∵AD是△ABC的高,
∴∠ADB=90°,
∴∠BAD=180°﹣∠ABD﹣∠ADB=30°;
(2)由题意可知:∠C=70°﹣30°=40°,
∴∠BAC=180°﹣∠ABC﹣∠C=80°,
∵AE平分∠BAC,
∴∠BAE=40°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣30°=10°.
20.解:∵∠A=35°,∠ABD=35°,
∴∠BDC=∠A+∠ABD=70°,
∵CE平分∠ACB,∠ACB=80°,
∴∠DCE∠ACB=40°,
∴∠BEC=∠BDC+∠DCE=70°+40°=110°.
21.解:(1)如图1,∵AD平分∠BAC,
∴∠CAD∠BAC,
∵AE⊥BC,
∴∠CAE=90°﹣∠C,
∴∠DAE=∠CAD﹣∠CAE
∠BAC﹣(90°﹣∠C)
(180°﹣∠B﹣∠C)﹣(90°﹣∠C)
∠C∠B
(∠C﹣∠B),
∵∠B=50°,∠C=70°,
∴∠DAE(70°﹣50°)=10°.
(2)结论:∠DEF(∠C﹣∠B).
理由:如图2,过A作AG⊥BC于G,
∵EF⊥BC,
∴AG∥EF,
∴∠DAG=∠DEF,
由(1)可得,∠DAG(∠C﹣∠B),
∴∠DEF(∠C﹣∠B).
(3)仍成立.
如图3,过A作AG⊥BC于G,
∵EF⊥BC,
∴AG∥EF,
∴∠DAG=∠DEF,
由(1)可得,∠DAG(∠C﹣∠B),
∴∠DEF(∠C﹣∠B),
答案为∠DEF(∠C﹣∠B).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025年数学寒假知识巩固练习题第11章三角形
复习范围:第11章三角形;考试时间:60分钟;
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共9小题)
1.以下列数值为长度的各组线段中,能组成三角形的是( )
A.2,4,7 B.3,3,6 C.5,8,2 D.4,5,6
2.如图,要使五边形木架(用5根木条钉成)不变形,至少再钉木条的根数为( )
A.5根 B.4根 C.3根 D.2根
3.嘉嘉家、琪琪家和学校不在同一直线上,嘉嘉家和琪琪家到学校的直线距离分别是2km和3km他们两家的直线距离可能是( )
A.1km B.4km C.5km D.6km
4.如图表示三角形的分类,则A表示的是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.三边都不相等的三角形
5.如图,在△ABC中,边AB上的高是( )
A.线段AF B.线段BE C.线段CE D.线段BD
(5题图) (6题图) (7题图) (8题图) (9题图)
6.点O是△ABC内一点,OA、OC分别平分∠BAC、∠BCA,∠B=64°,则∠O=( )
A.116° B.122° C.136° D.152°
7.如图是由一副常规直角三角板摆放得到的图形,图中的∠ABF的度数为( )
A.30° B.15° C.60° D.25°.
8.如图CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,求∠BAC与∠B,∠E的关系是( )
A.∠BAC=∠B+∠E B.∠BAC=∠B+2∠E C.∠BAC=2∠B+∠E D.
9.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是( )
A.∠1+∠2=90° B.∠1+∠4=90° C.∠2+∠4=90° D.∠2=∠3
二.填空题(共8小题)
10.若△ABC三条边长为a,b,c化简:|a﹣b﹣c|+|a+c﹣b|= .
11.如图,已知AE是△ABC的边BC上的中线,若AC=6,△AEC的周长比△AEB的周长多1,则AB= .
12.若一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是 .
13.如图,在△ABC中,高AD=2,CE=4,则AB与BC的比值是 .
(13题图) (14题图) (16题图) (17题图)
14.如图,在△ABC中,∠ACB=80°,点D在AB上,将△ABC沿CD折叠,点B落在边AC的点E处.若∠ADE=24°,则∠A的度数为 °.
15.一个多边形的内角和等于外角和的4倍,则从这个多边形一个顶点可以引 条对角线.
16.如图,在同一平面内,将边长相等的正六边形、正方形的一边重合,则∠1的度数为 .
17.如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7= .
三.解答题(共4小题)
18.如图所示,D是△ABC的边BC上的一点,且∠1=∠2,∠3=∠4,∠BAC=63°,则∠DAC的度数.
19.如图,AD是△ABC的高,AE、BF是△ABC的角平分线,且∠CBF=30°.
(1)求∠BAD的度数;
(2)若∠AFB=70°,求∠DAE的度数.
20.如图,在△ABC中,∠A=35°,∠ABD=35°,∠ACB=80°,且CE平分∠ACB,求∠BEC的度数.
21.在△ABC中,AD是角平分线,∠B<∠C,
(1)如图(1),AE是高,∠B=50°,∠C=70°,求∠DAE的度数;
(2)如图(2),点E在AD上.EF⊥BC于F,试探究∠DEF与∠B、∠C的大小关系,并证明你的结论;
(3)如图(3),点E在AD的延长线上.EF⊥BC于F,试探究∠DEF与∠B、∠C的关系是 (直接写出结论,不需证明).
参考答案
一.选择题(共9小题)
1.解:A、4+2=6<7,不能组成三角形;
B、3+3=6,不能组成三角形;
C、5+2=7<8,不能组成三角形;
D、4+5=9>6,能组成三角形.
选:D.
2.解:如图所示,由三角形具有稳定性可知:要使五边形木架不变形,至少再钉2根木条,
选:D.
3.解:依题意有,设嘉嘉家和琪琪家的直线距离为d km,
则3﹣2≤d≤3+2,
即1≤d≤5.
选:B.
4.解:∵三角形按边分为三边都不等的三角形,等腰三角形,
∴A表示三边都不等的三角形.
选:D.
5.解:根据三角形的高的定义可知:线段CE是边AB边上的高,
选:C.
6.解:在△ABC中,∠B=64°,
∴∠BAC+∠BCA=180°﹣∠B=180°﹣64°=116°.
∵OA、OC分别平分∠BAC、∠BCA,
∴∠OAC∠BAC,∠OCA∠BCA,
∴∠OAC+∠OCA∠BAC∠BCA(∠BAC+∠BCA)116°=58°.
在△OAC中,∠OAC+∠OCA=58°,
∴∠O=180°﹣(∠OAC+∠OCA)=180°﹣58°=122°.
选:B.
7.解:由题意得:∠DAE=45°,
∵∠F=30°,∠DAE是△ABF的外角,
∴∠ABF=∠DAE﹣∠F=45°﹣30°=15°.
选:B.
8.解:∠BAC=∠B+2∠E,
理由:
∵CE是△ABC的外角∠ACD的平分线,
∴∠ACE=∠ECD,
∵∠BAC=∠ACE+∠E,
∠ECD=∠ACE=∠B+∠E,
∴∠BAC=∠B+∠E+∠E=∠B+2∠E.
选:B.
9.解:Rt△ABC中,
∵∠ACB=90°,
∴∠1+∠2=90°,A正确;
∵CD⊥AB,
∴∠ADC=90°,
∴∠1+∠3=90°,
∴∠2=∠3,D正确;
∵∠3+∠4=90°,
∴∠1=∠4,B不正确;
∵∠2+∠4=90°,C正确;
选:B.
二.填空题(共8小题)
10.解:a﹣b<c,a+c>b,
|a﹣b﹣c|+|a+c﹣b|
=c﹣(a﹣b)+a+c﹣b
=2c.
答案为:2c.
11.解:∵AE是△ABC的边BC上的中线,
∴CE=BE,
∵△ACE的周长比△AEB的周长多1,
∴(AC+AE+CE)﹣(AB+BE+AE)=1,即AC﹣AB=1,
∵AC=6,
∴AB=5,
答案为:5.
12.解:因为直角三角形的直角所在的顶点正好是三条高线的交点,所以可以得出这个三角形是直角三角形.
答案为:直角三角形.
13.解:S△ABCAB CEBC AD,
∴4AB=2BC,
∴,
答案为:.
14.解:在△ABC中,∠ACB=80°,
∴∠B=180°﹣∠A﹣∠ACB
=100°﹣∠A,
∵将△ABC沿CD折叠,点B落在边AC的点E处,
∴∠CED=∠B=100°﹣∠A,
∵∠CED是△ADE的一个外角,∠ADE=24°,
∴∠CED=∠A+∠ADE,
即,100°﹣∠A=∠A+24°
解得:∠A=38°.
答案为:38.
15.解:设这个正多边形的边数是n,则
(n﹣2) 180°=1440°,
解得:n=10.
则从这个多边形一个顶点可以引7条对角线.
16.解:正六边形的一个内角的度数为,正方形的一个内角的度数为90°,
由图可知:∠1=120°﹣90°=30°;
答案为:30°.
17.解:如图,
∵∠3+∠4+8=180°①,
∠6+∠7+∠10+∠11=360°②,
∠1+∠2+∠5+∠9=360°③,
∴①+②+③得,∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠9+∠10+∠11+∠12=900°,
∵∠8+∠10=180°,∠9+∠11=180°,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7
=900°﹣180°﹣180°
=540°.
答案为:540°.
三.解答题(共4小题)
18.解:∵∠3=∠1+∠2,∠1=∠2,∠3=∠4,
∴∠4=2∠2.
∵∠2+∠4+∠BAC=180°,∠BAC=63°,
∴3∠2+63°=180°,
∴∠2=39°,
∴∠1=∠2=39°,
∴∠DAC=63°﹣39°=24°.
19.解:(1)由题意可知:∠ABC=2∠CBF=60°,
∵AD是△ABC的高,
∴∠ADB=90°,
∴∠BAD=180°﹣∠ABD﹣∠ADB=30°;
(2)由题意可知:∠C=70°﹣30°=40°,
∴∠BAC=180°﹣∠ABC﹣∠C=80°,
∵AE平分∠BAC,
∴∠BAE=40°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣30°=10°.
20.解:∵∠A=35°,∠ABD=35°,
∴∠BDC=∠A+∠ABD=70°,
∵CE平分∠ACB,∠ACB=80°,
∴∠DCE∠ACB=40°,
∴∠BEC=∠BDC+∠DCE=70°+40°=110°.
21.解:(1)如图1,∵AD平分∠BAC,
∴∠CAD∠BAC,
∵AE⊥BC,
∴∠CAE=90°﹣∠C,
∴∠DAE=∠CAD﹣∠CAE
∠BAC﹣(90°﹣∠C)
(180°﹣∠B﹣∠C)﹣(90°﹣∠C)
∠C∠B
(∠C﹣∠B),
∵∠B=50°,∠C=70°,
∴∠DAE(70°﹣50°)=10°.
(2)结论:∠DEF(∠C﹣∠B).
理由:如图2,过A作AG⊥BC于G,
∵EF⊥BC,
∴AG∥EF,
∴∠DAG=∠DEF,
由(1)可得,∠DAG(∠C﹣∠B),
∴∠DEF(∠C﹣∠B).
(3)仍成立.
如图3,过A作AG⊥BC于G,
∵EF⊥BC,
∴AG∥EF,
∴∠DAG=∠DEF,
由(1)可得,∠DAG(∠C﹣∠B),
∴∠DEF(∠C﹣∠B),
答案为∠DEF(∠C﹣∠B).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
