2025年数学寒假知识巩固第12章全等三角形辅助线及模型专练(含解析)
文档属性
| 名称 | 2025年数学寒假知识巩固第12章全等三角形辅助线及模型专练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年数学寒假知识巩固练习题第12章全等三角形辅助线及模型专练
复习范围:第12章全等三角形;考试时间:60分钟;
学校:___________姓名:___________班级:___________考号:___________
一.利用公共边构造全等三角形
1.如图,AB=AC,BD=CD.
(1)求证:∠B=∠C;
(2)若∠BAC=120°,∠BDC=80°,求∠B的度数.
2.如图,AB=AC,BD=CD.求证:
(1)∠B=∠C;
(2)∠BDC=2∠B+∠BAC.
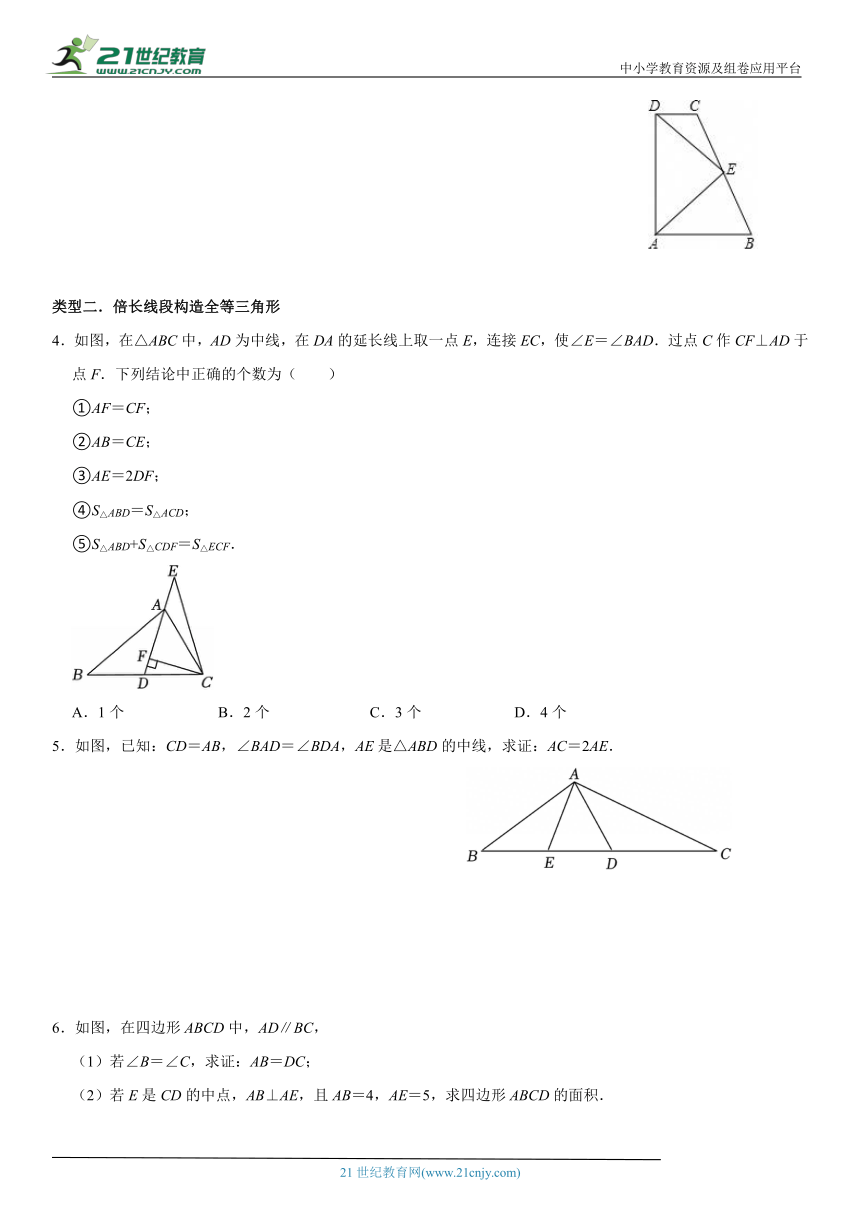
3.如图,DC∥AB,∠BAD和∠ADC的角平分线相交于E,过E的直线分别交DC,AB于CB两点.
(1)判断AE与DE的位置关系.并说明理由;
(2)求证:AD=AB+DC
类型二.倍长线段构造全等三角形
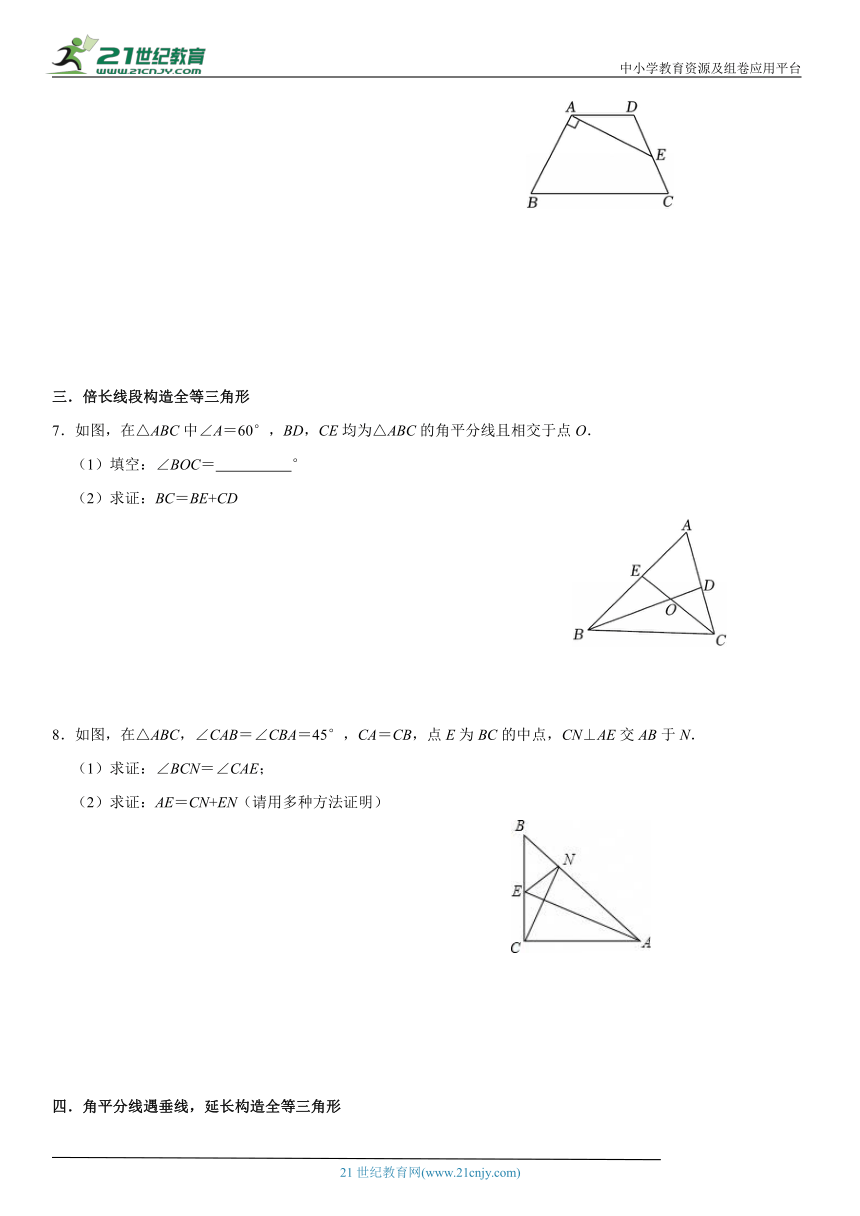
4.如图,在△ABC中,AD为中线,在DA的延长线上取一点E,连接EC,使∠E=∠BAD.过点C作CF⊥AD于点F.下列结论中正确的个数为( )
①AF=CF;
②AB=CE;
③AE=2DF;
④S△ABD=S△ACD;
⑤S△ABD+S△CDF=S△ECF.
A.1个 B.2个 C.3个 D.4个
5.如图,已知:CD=AB,∠BAD=∠BDA,AE是△ABD的中线,求证:AC=2AE.
6.如图,在四边形ABCD中,AD∥BC,
(1)若∠B=∠C,求证:AB=DC;
(2)若E是CD的中点,AB⊥AE,且AB=4,AE=5,求四边形ABCD的面积.
三.倍长线段构造全等三角形
7.如图,在△ABC中∠A=60°,BD,CE均为△ABC的角平分线且相交于点O.
(1)填空:∠BOC= °
(2)求证:BC=BE+CD
8.如图,在△ABC,∠CAB=∠CBA=45°,CA=CB,点E为BC的中点,CN⊥AE交AB于N.
(1)求证:∠BCN=∠CAE;
(2)求证:AE=CN+EN(请用多种方法证明)
四.角平分线遇垂线,延长构造全等三角形
9.如图,△ABC的面积为8cm2,AP垂直∠B的平分线BP于点P,则△PBC的面积为 cm2.
10.如图,已知在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC,CE⊥BD交BD的延长线于点E.
求证:CEBD.
11.如图.在△ABC中,BE是角平分线,AD⊥BE,垂足为D,求证:∠2=∠1+∠C.
五.作垂线法
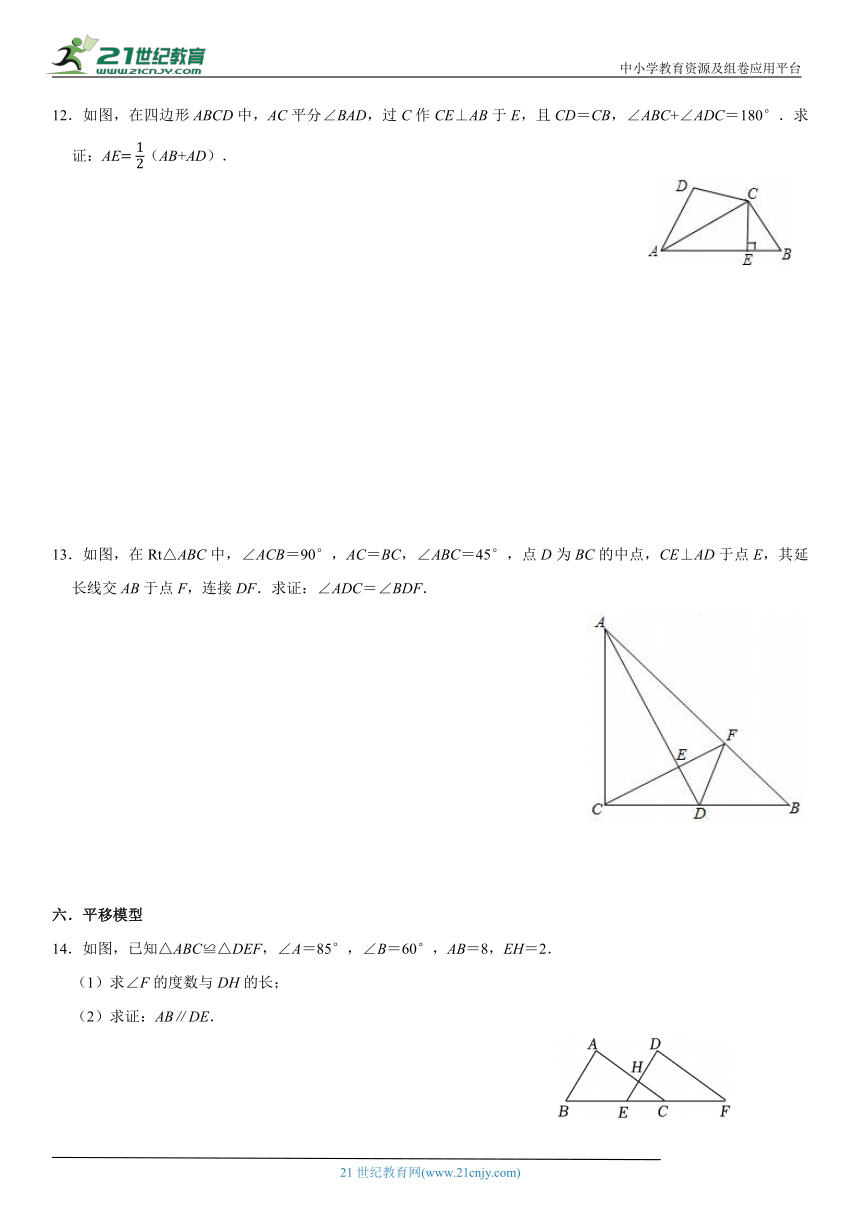
12.如图,在四边形ABCD中,AC平分∠BAD,过C作CE⊥AB于E,且CD=CB,∠ABC+∠ADC=180°.求证:AE(AB+AD).
13.如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.
六.平移模型
14.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求∠F的度数与DH的长;
(2)求证:AB∥DE.
15.如图,点B、C、E、F在同一直线上,AB⊥BC于点B,△DEF≌△ABC,且BC=6,CE=2.
(1)求CF的长;
(2)判断DE与EF的位置关系,并说明理由.
七.对称模型
16.如图,已知点D为△ABC的边BC的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且BF=CE.
求证:
(1)AB=AC;
(2)AD平分∠BAC.
17.如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,BD与CE相交于点O.
(1)求证:BD=CE;
(2)若∠ABC=50°,求∠BOC的度数.
八.一线三等角模型
18.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图(1)的位置时,
求证:①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图(3)的位置时,请直接写出DE,AD,BE之间的等量关系.
19.如图,△ABC的两条高AD,CE交于点F,AF=BC.
(1)求证:BE=EF;
(2)若BE=4,CF=5,求△ACF的面积.
20.如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E在同一直线上,连接BD.
(1)求证:△BAD≌△CAE.
(2)请写出BD,CE的关系,并证明.
九.半角模型
21.已知,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD上的点,且∠EAF∠BAD.
(1)为探究上述问题,小王同学先画出了其中一种特殊情况,即如图1,当∠B=∠ADC=90°时.
小王同学探究此问题的方法是:延长FD到点G,使DG=BE,连接AG.
请你在图1中添加上述辅助线,并补全下面的思路.
小明的解题思路:先证明△ABE≌ ;再证明了△AEF≌ ,即可得出BE,EF,FD之间的数量关系为 .
(2)请你借鉴小王的方法探究图2,当∠B+∠ADC=180°时,上述结论是否依然成立,如果成立,请证明你的结论,如果不成立,请说明理由.
(3)如图3,若E、F分别是边BC、CD延长线上的点,其他已知条件不变,此时线段EF、BE、FD之间的数量关系为 .(不用证明)
参考答案
1.证明:(1)连接AD,如图:
在△ABD与△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠B=∠C;
(2)∵△ABD≌△ACD,
∴∠B=∠C,
在四边形ABCD中,∠B.
2.(1)证明:如图,连接AD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠B=∠C.
(2)证明:如图,延长AD至点E,
∵∠BDE=∠B+∠BAD,∠CDE=∠C+∠CAD,
∴∠BDC=∠BDE+∠CDE=∠B+∠C+∠BAD+∠CAD=∠B+∠C+∠BAC,
由(1)已证:∠B=∠C,
∴∠BDC=2∠B+∠BAC.
3.解:(1)AE⊥DE,
理由:∵DC∥AB,
∴∠BAD+∠ADC=180°,
∵∠BAD和∠ADC的角平分线相交于E,
∴∠3∠ADC,∠1∠BAD,
∴∠1+∠3(∠BAD+∠ADC)180°=90°,
∴∠AED=90°,
∴AE⊥DE;
(2)在AD上截取AF=AB,连接EF,如图所示:
在△ABE和△AFE中,,
∴△ABE≌△AFE(SAS),
∴∠AFE=∠B,
∵AB∥DC,
∴∠B+∠C=180°,
∵∠AFE+∠DFE=180°,
∴∠DFE=∠C,
在△DEF和△DEC中,,
∴△DEF≌△DEC(AAS),
∴DF=DC,
∴AB+DC=AF+DF=AD,
即AD=AB+DC.
4.解:过点B作BG⊥AD于点G,
∵AD为中线,
∴BD=CD.
∵BG⊥AD,CF⊥AD,
∴∠G=∠CFD=90°,
∵∠BDG=∠CDF,
△BDG≌△CDF(AAS),
∴AB=CE,BG=CF,DG=DF,故②正确;①错误;
∵∠E=∠BAD,
∴△ABG≌△ECF(AAS),
∴AG=EF,
∴AE=GF,
∴AE=2DF,故③正确;
∵BD=CD,
∴S△ABD=2S△ADC,故④正确;
∴S△ABD=S△ACD,
∵AE=2DF,
∴S△AEC=2S△CDF,
∴S△ABD+S△CDF=S△ACD+S△CDF
=S△ACF+S△CDF+S△CDF
=S△ACF+2S△CDF
=S△ACF+S△AEC
=S△ECF,
∴⑤故正确.
故选:D.
5.证明:延长AE至F,使AE=EF,连接BF,
在△ADE与△BFE中,
,
∴△AED≌△FEB(SAS),
∴BF=DA,∠FBE=∠ADE,
∵∠ABF=∠ABD+∠FBE,
∴∠ABF=∠ABD+∠ADB=∠ABD+∠BAD=∠ADC,
在△ABF与△ADC中,
,
∴△ABF≌△CDA(SAS),
∴AC=AF,
∵AF=2AE,
∴AC=2AE.
6.(1)证明:如图,延长BA,CD相交于点G,
∵∠B=∠DCB,
∴GB=GC,
∵AD∥BC,
∴∠GAD=∠B,∠GDA=∠DCB,
∴∠GAD=∠GDA,
∴GA=GD,
∴GB﹣GA=GC﹣GD,
即AB=DC.
(2)解:延长AE交BC的延长线于F,
∵AD∥BC,
∴∠DAE=∠F,∠ADE=∠FCE,
∵E是CD的中点,
∴DE=CE,
∴△ADE≌△FCE(AAS),
∴EF=AE=5,
∴AF=2×5=10,
∴S四边形ABCD=S△ABFAB AF4×10=20.
7.(1)解:∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣60°=120°;
∵BD,CE均为△ABC的角平分线,
∴∠OBC∠ABC,∠OCB∠ACB,
∴∠OBC+∠OCB(∠ABC+∠ACB)=60°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣60°=120°,
故答案为:120;
(2)证明:在BC上截取BF=BE,如图,
∵OB平分∠ABC,
∴∠ABO=∠CBO,
在△BOE和△BOF中,
,
∴△BOE≌△BOF(SAS),
∴∠BOE=∠BOF,
∵∠BOC=120°,
∴∠BOE=∠COD=60°,
∴∠BOF=60°,
∵OC平分∠ACB,
∴∠ACO=∠BCO,
在△COD和△COF中,
,
∴△COD≌△COF(ASA),
∴CD=CF,
∴BC=BF+CF=BE+CD.
8.证明:(1)∵∠CAB=∠CBA=45°,
∴∠ACB=90°,
∵CN⊥AE,
∴∠COE=90°,
∴∠CEA+∠1=90°,∠CEA+∠2=90°,
∴∠BCN=∠CAE;
(2)法一:如图1,延长CN至F,使CF=AE,连接BF,
在△CAE和△BCF中
,
∴△CAE≌△BCF(SAS),
∴∠ACE=∠CBF=90°,CE=BF,
∵∠CBA=45°,
∴∠FBN=45°=∠EBN,
∵E为BC中点,
∴CE=BE=BF,
在△EBN和△FBN中,
,
∴△EBN≌△FBN(SAS),
∴NE=NF,
∴AE=CN+EN.
法二:如图2,在AE上截取AF=CN,
在△ACF和△CBN中,
,
∴△ACF≌△CBN,
∴CF=BN,∠ACF=∠B=45°,
∴∠ECF=45°=∠B,
在△BEN和△CEF中,
,
∴△BEN≌△CEF,
∴EN=EF,
∴AE=AF+EF=CN+EN.
9.解:延长AP交BC于E,
∵AP垂直∠B的平分线BP于P,
∠ABP=∠EBP,
又知BP=BP,∠APB=∠BPE=90°,
∴△ABP≌△BEP,
∴S△ABP=S△BEP,AP=PE,
∴△APC和△CPE等底同高,
∴S△APC=S△PCE,
∴S△PBC=S△PBE+S△PCES△ABC=4cm2,
故答案为:4.
10.证明:如图,延长CE,BA交于点F.
∵CE⊥BD,∠BAC=90°,
∴∠BAD=∠CAF=∠BEC=90°.
又∵∠ADB=∠EDC,
∴∠ABD=∠ACF.
在△ABD与△ACF中,
∴△ABD≌△ACF(ASA).
∴BD=CF.
∵BD平分∠ABC,
∴∠CBE=∠FBE.
在△BCE与△BFE中,
∴△BCE≌△BFE(ASA).
∴CE=FE,即CECF.
∴CEBD.
11.证明:如图,延长AD交BC于点F,
∵BE是角平分线,AD⊥BE,
∴△ABF是等腰三角形,且∠2=∠AFB,
又∵∠AFB=∠1+∠C,
∴∠2=∠1+∠C.
12.证明:过C作CM⊥AD于M,
∵CE⊥AB,
∴∠M=∠CEB=90°,
∵∠ABC+∠ADC=180°,∠ADC+∠MDC=180°,
∴∠B=∠MDC,
∵AC平分∠BAD,CM⊥AD,CE⊥AB,
∴CM=CE,∠MAC=∠EAC,
在△MAC和△EAC中,
,
∴△MAC≌△EAC(AAS),
∴AM=AE,
∵∠ABC+∠ADC=180°,∠ADC+∠MDC=180°,
∴∠ABC=∠MDC,CM=CE,
∴Rt△DMC≌Rt△BEC(AAS),
∴BE=DM,
∴AB+AD
=AE+BE+AD
=AE+DM+AD
=2AM
=2AE,
即AE(AB+AD).
13.证明:作BG⊥CB,交CF的延长线于点G,如图所示:
∵∠CBG=90°,CF⊥AD,
∴∠CAD+∠ADC=∠BCG+∠ADC=90°,
∴∠CAD=∠BCG,
在△ACD和△CBG中,
,
∴△ACD≌△CBG(ASA),
∴CD=BG,∠CDA=∠CGB,
∵CD=BD,
∴BG=BD,
∵∠ABC=45°,
∴∠FBD=∠GBF∠CBG,
在△BFG和△BFD中,
,
∴△BFG≌△BFD(SAS),
∴∠FGB=∠FDB,
∴∠ADC=∠BDF.
14.解:(1)∵∠A=85°,∠B=60°,
∴∠ACB=180°﹣∠A﹣∠B=35°,
∵△ABC≌△DEF,AB=8,
∴∠F=∠ACB=35°,DE=AB=8,
∵EH=2,
∴DH=8﹣2=6;
(2)证明:∵△ABC≌△DEF,
∴∠DEF=∠B,
∴AB∥DE.
15.解:(1)∵△DEF≌△ABC,
∴EF=BC=6,
∵CE=2,
∴CF=CE+EF=2+6=8;
(2)DE⊥EF,理由如下:
∵AB⊥BC,
∴∠ABC=90°
∵△DEF≌△ABC,
∴∠DEF=∠ABC=90°,
∴DE⊥EF.
16.证明:(1)∵D是BC的中点,
∴BD=CD.
∵DE⊥AC,DF⊥AB,
∴△CDE与△BDF均为直角三角形,
∵BF=CE,
∴Rt△BDF≌Rt△CDE(HL),
∴∠B=∠C,
∴AB=AC.
(2)∵Rt△BDF≌Rt△CDE(HL),
∴DF=DE.
又∵DE⊥AC,DF⊥AB,
∴AD平分∠BAC.
17.(1)证明:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°,
在△ADB和△AEC中,
,
∴△ADB≌△AEC(AAS),
∴BD=CE.
(2)解:∵AB=AC,
∴∠ACB=∠ABC=50°,
∴∠A=180°﹣50°﹣50°=80°,
∵∠ADB=∠AEC=90°,
∴∠DOE=360°﹣90°﹣90°﹣80°=100°,
∴∠BOC=∠DOE=100°,
∴∠BOC的度数是100°.
18.解:(1)①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠ACB=90°=∠CEB,
∴∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
∵在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
②∵△ADC≌△CEB,
∴CE=AD,CD=BE,
∴DE=CE+CD=AD+BE;
(2)证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=∠ACB=90°,
∴∠CAD=∠BCE,
∵在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
∴CE=AD,CD=BE,
∴DE=CE﹣CD=AD﹣BE;
(3)当MN旋转到题图(3)的位置时,AD,DE,BE所满足的等量关系是:DE=BE﹣AD.
理由如下:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=∠ACB=90°,
∴∠CAD=∠BCE,
∵在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS),
∴CE=AD,CD=BE,
∴DE=CD﹣CE=BE﹣AD.
19.(1)证明:∵△ABC的两条高AD,CE交于点F,
∴∠BEC=∠AEC=90°,
∴∠BCE+∠B=∠DAB+∠B=90°,
∴∠BCE=∠DAB,
在△BCE和△AEF中,
,
∴△BCE≌△FAE(AAS),
∴BE=EF;
(2)解:∵△BCE≌△FAE,
∴AE=CE,
而BE=4,CF=5,
∴EF=4,
∴CE=AE=9,
∴S△ACFCF×AE5×9.
20.(1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS);
(2)解:BD=CE,BD⊥CE,理由如下:
由(1)知,△BAD≌△CAE,
∴BD=CE,∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE.
21.(1)证明:如图1中,延长FD到点G,使DG=BE,连接AG.
∵∠ADG=∠ABC=∠ADF=90°,AB=AD,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠1=∠2,
∴∠1+∠3=∠2+∠3=∠EAF∠BAD,
∴∠GAF=∠EAF,
∵AF=AF,
∴△AEF≌△AGF(SAS),
∴EF=EG,
∵FG=FD+DG,
∴EF=DF+BE,
故答案为:△ADG,△AEG,EF=BE+FD;
(2)解:上述结论依然成立.
证明:如图2,延长CB至M,使BM=DF,连接AM.
∵∠ABC+∠D=180°,∠1+∠ABC=180°,
∴∠1=∠D,
在△ABM与△ADF中,
,
∴△ABM≌△ADF(SAS).
∴AF=AM,∠2=∠3.
∵∠EAF∠BAD,
∴∠2+∠4=∠3+∠4=∠MAE,
∴∠MAE=∠FAE,
在△AME与△AFE中,
,
∴△AME≌△AFE(SAS).
∴EF=ME.
∴EF=ME=BE+BM=BE+DF;
(3)解:在BE上截取BG,使BG=DF,连接AG,
∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,
∴∠B=∠ADF,
在△ABG与△ADF中,
,
∴△ABG≌△ADF(SAS),
∴∠BAG=∠DAF,AG=AF,
∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF∠BAD,
∴∠GAE=∠EAF.
∵AE=AE,
∴△AEG≌△AEF(SAS),
∴EG=EF,
∵EG=BE﹣BG,
∴EF=BE﹣FD.
故答案为:EF=BE﹣FD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025年数学寒假知识巩固练习题第12章全等三角形辅助线及模型专练
复习范围:第12章全等三角形;考试时间:60分钟;
学校:___________姓名:___________班级:___________考号:___________
一.利用公共边构造全等三角形
1.如图,AB=AC,BD=CD.
(1)求证:∠B=∠C;
(2)若∠BAC=120°,∠BDC=80°,求∠B的度数.
2.如图,AB=AC,BD=CD.求证:
(1)∠B=∠C;
(2)∠BDC=2∠B+∠BAC.
3.如图,DC∥AB,∠BAD和∠ADC的角平分线相交于E,过E的直线分别交DC,AB于CB两点.
(1)判断AE与DE的位置关系.并说明理由;
(2)求证:AD=AB+DC
类型二.倍长线段构造全等三角形
4.如图,在△ABC中,AD为中线,在DA的延长线上取一点E,连接EC,使∠E=∠BAD.过点C作CF⊥AD于点F.下列结论中正确的个数为( )
①AF=CF;
②AB=CE;
③AE=2DF;
④S△ABD=S△ACD;
⑤S△ABD+S△CDF=S△ECF.
A.1个 B.2个 C.3个 D.4个
5.如图,已知:CD=AB,∠BAD=∠BDA,AE是△ABD的中线,求证:AC=2AE.
6.如图,在四边形ABCD中,AD∥BC,
(1)若∠B=∠C,求证:AB=DC;
(2)若E是CD的中点,AB⊥AE,且AB=4,AE=5,求四边形ABCD的面积.
三.倍长线段构造全等三角形
7.如图,在△ABC中∠A=60°,BD,CE均为△ABC的角平分线且相交于点O.
(1)填空:∠BOC= °
(2)求证:BC=BE+CD
8.如图,在△ABC,∠CAB=∠CBA=45°,CA=CB,点E为BC的中点,CN⊥AE交AB于N.
(1)求证:∠BCN=∠CAE;
(2)求证:AE=CN+EN(请用多种方法证明)
四.角平分线遇垂线,延长构造全等三角形
9.如图,△ABC的面积为8cm2,AP垂直∠B的平分线BP于点P,则△PBC的面积为 cm2.
10.如图,已知在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC,CE⊥BD交BD的延长线于点E.
求证:CEBD.
11.如图.在△ABC中,BE是角平分线,AD⊥BE,垂足为D,求证:∠2=∠1+∠C.
五.作垂线法
12.如图,在四边形ABCD中,AC平分∠BAD,过C作CE⊥AB于E,且CD=CB,∠ABC+∠ADC=180°.求证:AE(AB+AD).
13.如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.
六.平移模型
14.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求∠F的度数与DH的长;
(2)求证:AB∥DE.
15.如图,点B、C、E、F在同一直线上,AB⊥BC于点B,△DEF≌△ABC,且BC=6,CE=2.
(1)求CF的长;
(2)判断DE与EF的位置关系,并说明理由.
七.对称模型
16.如图,已知点D为△ABC的边BC的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且BF=CE.
求证:
(1)AB=AC;
(2)AD平分∠BAC.
17.如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,BD与CE相交于点O.
(1)求证:BD=CE;
(2)若∠ABC=50°,求∠BOC的度数.
八.一线三等角模型
18.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图(1)的位置时,
求证:①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图(3)的位置时,请直接写出DE,AD,BE之间的等量关系.
19.如图,△ABC的两条高AD,CE交于点F,AF=BC.
(1)求证:BE=EF;
(2)若BE=4,CF=5,求△ACF的面积.
20.如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E在同一直线上,连接BD.
(1)求证:△BAD≌△CAE.
(2)请写出BD,CE的关系,并证明.
九.半角模型
21.已知,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD上的点,且∠EAF∠BAD.
(1)为探究上述问题,小王同学先画出了其中一种特殊情况,即如图1,当∠B=∠ADC=90°时.
小王同学探究此问题的方法是:延长FD到点G,使DG=BE,连接AG.
请你在图1中添加上述辅助线,并补全下面的思路.
小明的解题思路:先证明△ABE≌ ;再证明了△AEF≌ ,即可得出BE,EF,FD之间的数量关系为 .
(2)请你借鉴小王的方法探究图2,当∠B+∠ADC=180°时,上述结论是否依然成立,如果成立,请证明你的结论,如果不成立,请说明理由.
(3)如图3,若E、F分别是边BC、CD延长线上的点,其他已知条件不变,此时线段EF、BE、FD之间的数量关系为 .(不用证明)
参考答案
1.证明:(1)连接AD,如图:
在△ABD与△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠B=∠C;
(2)∵△ABD≌△ACD,
∴∠B=∠C,
在四边形ABCD中,∠B.
2.(1)证明:如图,连接AD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠B=∠C.
(2)证明:如图,延长AD至点E,
∵∠BDE=∠B+∠BAD,∠CDE=∠C+∠CAD,
∴∠BDC=∠BDE+∠CDE=∠B+∠C+∠BAD+∠CAD=∠B+∠C+∠BAC,
由(1)已证:∠B=∠C,
∴∠BDC=2∠B+∠BAC.
3.解:(1)AE⊥DE,
理由:∵DC∥AB,
∴∠BAD+∠ADC=180°,
∵∠BAD和∠ADC的角平分线相交于E,
∴∠3∠ADC,∠1∠BAD,
∴∠1+∠3(∠BAD+∠ADC)180°=90°,
∴∠AED=90°,
∴AE⊥DE;
(2)在AD上截取AF=AB,连接EF,如图所示:
在△ABE和△AFE中,,
∴△ABE≌△AFE(SAS),
∴∠AFE=∠B,
∵AB∥DC,
∴∠B+∠C=180°,
∵∠AFE+∠DFE=180°,
∴∠DFE=∠C,
在△DEF和△DEC中,,
∴△DEF≌△DEC(AAS),
∴DF=DC,
∴AB+DC=AF+DF=AD,
即AD=AB+DC.
4.解:过点B作BG⊥AD于点G,
∵AD为中线,
∴BD=CD.
∵BG⊥AD,CF⊥AD,
∴∠G=∠CFD=90°,
∵∠BDG=∠CDF,
△BDG≌△CDF(AAS),
∴AB=CE,BG=CF,DG=DF,故②正确;①错误;
∵∠E=∠BAD,
∴△ABG≌△ECF(AAS),
∴AG=EF,
∴AE=GF,
∴AE=2DF,故③正确;
∵BD=CD,
∴S△ABD=2S△ADC,故④正确;
∴S△ABD=S△ACD,
∵AE=2DF,
∴S△AEC=2S△CDF,
∴S△ABD+S△CDF=S△ACD+S△CDF
=S△ACF+S△CDF+S△CDF
=S△ACF+2S△CDF
=S△ACF+S△AEC
=S△ECF,
∴⑤故正确.
故选:D.
5.证明:延长AE至F,使AE=EF,连接BF,
在△ADE与△BFE中,
,
∴△AED≌△FEB(SAS),
∴BF=DA,∠FBE=∠ADE,
∵∠ABF=∠ABD+∠FBE,
∴∠ABF=∠ABD+∠ADB=∠ABD+∠BAD=∠ADC,
在△ABF与△ADC中,
,
∴△ABF≌△CDA(SAS),
∴AC=AF,
∵AF=2AE,
∴AC=2AE.
6.(1)证明:如图,延长BA,CD相交于点G,
∵∠B=∠DCB,
∴GB=GC,
∵AD∥BC,
∴∠GAD=∠B,∠GDA=∠DCB,
∴∠GAD=∠GDA,
∴GA=GD,
∴GB﹣GA=GC﹣GD,
即AB=DC.
(2)解:延长AE交BC的延长线于F,
∵AD∥BC,
∴∠DAE=∠F,∠ADE=∠FCE,
∵E是CD的中点,
∴DE=CE,
∴△ADE≌△FCE(AAS),
∴EF=AE=5,
∴AF=2×5=10,
∴S四边形ABCD=S△ABFAB AF4×10=20.
7.(1)解:∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣60°=120°;
∵BD,CE均为△ABC的角平分线,
∴∠OBC∠ABC,∠OCB∠ACB,
∴∠OBC+∠OCB(∠ABC+∠ACB)=60°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣60°=120°,
故答案为:120;
(2)证明:在BC上截取BF=BE,如图,
∵OB平分∠ABC,
∴∠ABO=∠CBO,
在△BOE和△BOF中,
,
∴△BOE≌△BOF(SAS),
∴∠BOE=∠BOF,
∵∠BOC=120°,
∴∠BOE=∠COD=60°,
∴∠BOF=60°,
∵OC平分∠ACB,
∴∠ACO=∠BCO,
在△COD和△COF中,
,
∴△COD≌△COF(ASA),
∴CD=CF,
∴BC=BF+CF=BE+CD.
8.证明:(1)∵∠CAB=∠CBA=45°,
∴∠ACB=90°,
∵CN⊥AE,
∴∠COE=90°,
∴∠CEA+∠1=90°,∠CEA+∠2=90°,
∴∠BCN=∠CAE;
(2)法一:如图1,延长CN至F,使CF=AE,连接BF,
在△CAE和△BCF中
,
∴△CAE≌△BCF(SAS),
∴∠ACE=∠CBF=90°,CE=BF,
∵∠CBA=45°,
∴∠FBN=45°=∠EBN,
∵E为BC中点,
∴CE=BE=BF,
在△EBN和△FBN中,
,
∴△EBN≌△FBN(SAS),
∴NE=NF,
∴AE=CN+EN.
法二:如图2,在AE上截取AF=CN,
在△ACF和△CBN中,
,
∴△ACF≌△CBN,
∴CF=BN,∠ACF=∠B=45°,
∴∠ECF=45°=∠B,
在△BEN和△CEF中,
,
∴△BEN≌△CEF,
∴EN=EF,
∴AE=AF+EF=CN+EN.
9.解:延长AP交BC于E,
∵AP垂直∠B的平分线BP于P,
∠ABP=∠EBP,
又知BP=BP,∠APB=∠BPE=90°,
∴△ABP≌△BEP,
∴S△ABP=S△BEP,AP=PE,
∴△APC和△CPE等底同高,
∴S△APC=S△PCE,
∴S△PBC=S△PBE+S△PCES△ABC=4cm2,
故答案为:4.
10.证明:如图,延长CE,BA交于点F.
∵CE⊥BD,∠BAC=90°,
∴∠BAD=∠CAF=∠BEC=90°.
又∵∠ADB=∠EDC,
∴∠ABD=∠ACF.
在△ABD与△ACF中,
∴△ABD≌△ACF(ASA).
∴BD=CF.
∵BD平分∠ABC,
∴∠CBE=∠FBE.
在△BCE与△BFE中,
∴△BCE≌△BFE(ASA).
∴CE=FE,即CECF.
∴CEBD.
11.证明:如图,延长AD交BC于点F,
∵BE是角平分线,AD⊥BE,
∴△ABF是等腰三角形,且∠2=∠AFB,
又∵∠AFB=∠1+∠C,
∴∠2=∠1+∠C.
12.证明:过C作CM⊥AD于M,
∵CE⊥AB,
∴∠M=∠CEB=90°,
∵∠ABC+∠ADC=180°,∠ADC+∠MDC=180°,
∴∠B=∠MDC,
∵AC平分∠BAD,CM⊥AD,CE⊥AB,
∴CM=CE,∠MAC=∠EAC,
在△MAC和△EAC中,
,
∴△MAC≌△EAC(AAS),
∴AM=AE,
∵∠ABC+∠ADC=180°,∠ADC+∠MDC=180°,
∴∠ABC=∠MDC,CM=CE,
∴Rt△DMC≌Rt△BEC(AAS),
∴BE=DM,
∴AB+AD
=AE+BE+AD
=AE+DM+AD
=2AM
=2AE,
即AE(AB+AD).
13.证明:作BG⊥CB,交CF的延长线于点G,如图所示:
∵∠CBG=90°,CF⊥AD,
∴∠CAD+∠ADC=∠BCG+∠ADC=90°,
∴∠CAD=∠BCG,
在△ACD和△CBG中,
,
∴△ACD≌△CBG(ASA),
∴CD=BG,∠CDA=∠CGB,
∵CD=BD,
∴BG=BD,
∵∠ABC=45°,
∴∠FBD=∠GBF∠CBG,
在△BFG和△BFD中,
,
∴△BFG≌△BFD(SAS),
∴∠FGB=∠FDB,
∴∠ADC=∠BDF.
14.解:(1)∵∠A=85°,∠B=60°,
∴∠ACB=180°﹣∠A﹣∠B=35°,
∵△ABC≌△DEF,AB=8,
∴∠F=∠ACB=35°,DE=AB=8,
∵EH=2,
∴DH=8﹣2=6;
(2)证明:∵△ABC≌△DEF,
∴∠DEF=∠B,
∴AB∥DE.
15.解:(1)∵△DEF≌△ABC,
∴EF=BC=6,
∵CE=2,
∴CF=CE+EF=2+6=8;
(2)DE⊥EF,理由如下:
∵AB⊥BC,
∴∠ABC=90°
∵△DEF≌△ABC,
∴∠DEF=∠ABC=90°,
∴DE⊥EF.
16.证明:(1)∵D是BC的中点,
∴BD=CD.
∵DE⊥AC,DF⊥AB,
∴△CDE与△BDF均为直角三角形,
∵BF=CE,
∴Rt△BDF≌Rt△CDE(HL),
∴∠B=∠C,
∴AB=AC.
(2)∵Rt△BDF≌Rt△CDE(HL),
∴DF=DE.
又∵DE⊥AC,DF⊥AB,
∴AD平分∠BAC.
17.(1)证明:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°,
在△ADB和△AEC中,
,
∴△ADB≌△AEC(AAS),
∴BD=CE.
(2)解:∵AB=AC,
∴∠ACB=∠ABC=50°,
∴∠A=180°﹣50°﹣50°=80°,
∵∠ADB=∠AEC=90°,
∴∠DOE=360°﹣90°﹣90°﹣80°=100°,
∴∠BOC=∠DOE=100°,
∴∠BOC的度数是100°.
18.解:(1)①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠ACB=90°=∠CEB,
∴∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
∵在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
②∵△ADC≌△CEB,
∴CE=AD,CD=BE,
∴DE=CE+CD=AD+BE;
(2)证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=∠ACB=90°,
∴∠CAD=∠BCE,
∵在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
∴CE=AD,CD=BE,
∴DE=CE﹣CD=AD﹣BE;
(3)当MN旋转到题图(3)的位置时,AD,DE,BE所满足的等量关系是:DE=BE﹣AD.
理由如下:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=∠ACB=90°,
∴∠CAD=∠BCE,
∵在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS),
∴CE=AD,CD=BE,
∴DE=CD﹣CE=BE﹣AD.
19.(1)证明:∵△ABC的两条高AD,CE交于点F,
∴∠BEC=∠AEC=90°,
∴∠BCE+∠B=∠DAB+∠B=90°,
∴∠BCE=∠DAB,
在△BCE和△AEF中,
,
∴△BCE≌△FAE(AAS),
∴BE=EF;
(2)解:∵△BCE≌△FAE,
∴AE=CE,
而BE=4,CF=5,
∴EF=4,
∴CE=AE=9,
∴S△ACFCF×AE5×9.
20.(1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS);
(2)解:BD=CE,BD⊥CE,理由如下:
由(1)知,△BAD≌△CAE,
∴BD=CE,∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE.
21.(1)证明:如图1中,延长FD到点G,使DG=BE,连接AG.
∵∠ADG=∠ABC=∠ADF=90°,AB=AD,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠1=∠2,
∴∠1+∠3=∠2+∠3=∠EAF∠BAD,
∴∠GAF=∠EAF,
∵AF=AF,
∴△AEF≌△AGF(SAS),
∴EF=EG,
∵FG=FD+DG,
∴EF=DF+BE,
故答案为:△ADG,△AEG,EF=BE+FD;
(2)解:上述结论依然成立.
证明:如图2,延长CB至M,使BM=DF,连接AM.
∵∠ABC+∠D=180°,∠1+∠ABC=180°,
∴∠1=∠D,
在△ABM与△ADF中,
,
∴△ABM≌△ADF(SAS).
∴AF=AM,∠2=∠3.
∵∠EAF∠BAD,
∴∠2+∠4=∠3+∠4=∠MAE,
∴∠MAE=∠FAE,
在△AME与△AFE中,
,
∴△AME≌△AFE(SAS).
∴EF=ME.
∴EF=ME=BE+BM=BE+DF;
(3)解:在BE上截取BG,使BG=DF,连接AG,
∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,
∴∠B=∠ADF,
在△ABG与△ADF中,
,
∴△ABG≌△ADF(SAS),
∴∠BAG=∠DAF,AG=AF,
∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF∠BAD,
∴∠GAE=∠EAF.
∵AE=AE,
∴△AEG≌△AEF(SAS),
∴EG=EF,
∵EG=BE﹣BG,
∴EF=BE﹣FD.
故答案为:EF=BE﹣FD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
