上海市静安区风华中学2024-2025学年高二上学期期末数学试卷(PDF版,含答案)
文档属性
| 名称 | 上海市静安区风华中学2024-2025学年高二上学期期末数学试卷(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 612.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 08:43:57 | ||
图片预览



文档简介
上海市静安区风华中学 2024-2025 学年高二上学期期末数学试卷
一、单选题:本题共 3 小题,每小题 5 分,共 15 分。在每小题给出的选项中,只有一项是符合题目要求的。
1.空间两条互相平行的直线指的是( )
A. 在空间没有公共点的两条直线
B. 分别在两个平面上的两条直线
C. 在两个不同的平面上且没有公共点的两条直线
D. 在同一平面上且没有公共点的两条直线
2.方程
2
16 =
5 5
16 的解集是( )
A. {1,3,5,7} B. {1,3,5} C. {3,5} D. {1,3}
3.祖暅,又名祖暅之,是我国南北朝时期的数学家、天文学家祖冲之的儿子.他在《级术》中提出“幂势既
同,则积不容异”的结论,其中“幂”是面积.“势”是高,意思就是:夹在两个平行平面间的两个几何体,
被平行于这两个平行平面的任一平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积
相等(如图①).这一原理主要应用于计算一些复杂几何体的体积,若某艺术品如图②所示,高为40 ,底面
为边长20 的正三角形挖去以底边为直径的圆(如图③),则该艺术品的体积为( )
1000 2000
A. (1000√ 3 ) 3 B. (2000√ 3 ) 3
3 3
2000√ 3 2000 3 1000√ 3 1000C. ( ) D. ( ) 3
3 9 3 9
二、填空题:本题共 10 小题,每小题 5 分,共 50 分。
4.空间中已知直线 ,直线 ,直线 ,若直线 //直线 ,直线 与直线 异面,则直线 与直线 的位置关系
是______.
2
5.在( + )5的二项展开式中, 3的系数是______(用数字作答).
6.甲、乙同时炮击一架敌机,已知甲击中敌机的概率为0.6,乙击中敌机的概率为0.5,敌机被击中的概率为
______.
第 1 页,共 8 页
7.球的表面积扩大为原来的4倍,它的体积扩大为原来的______ 倍.
8.甲、乙等五名社区志愿者被随机分配到 、 、 、 四个不同岗位服务,每个岗位至少有一名志愿者,则
甲、乙两人同时参加岗位 服务的排法有______种.
9.以下数据为参加数学竞赛决赛的15人的成绩(单位:分),分数从低到高依次:56,70,72,78,79,80,
81,83,84,86,88,90,91,94,98,则这15人成绩的第80百分位数是 .
10.有以下命题:
①若 = + ( , ∈ ),则 与 、 共面;
②若 与 、 共面,则 = + ( , ∈ );
③若 = + ( , ∈ ),则 、 、 、 共面;
④若 、 、 、 共面,则 = + ( , ∈ ).则所有真命题的序号为______.
11.如图是某班一次数学测试成绩的茎叶图(图中仅列出[50,60),[90,100)的数据)和频率分布直方图,则
= ______.
12.如图,在棱长为2的正方体 1 1 1 1中, 为线段 1 上的动点(不
含端点),则下列结论正确的是______.
①平面 1 1 ⊥平面 1 ;
② 1 ⊥ ;
③∠ 1的取值范围是[ , )2 ;
4
④三棱锥 1 1 的体积为定值 . 3
第 2 页,共 8 页
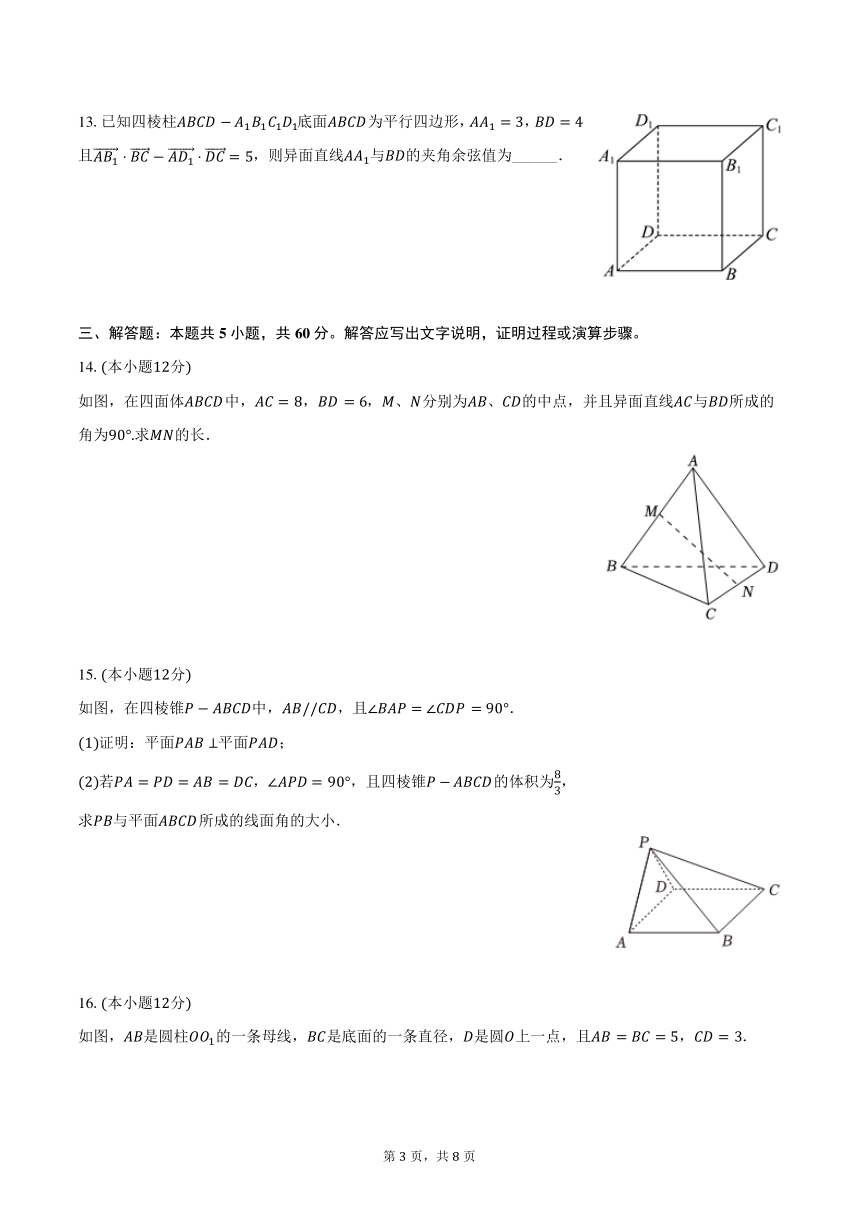
13.已知四棱柱 1 1 1 1底面 为平行四边形, 1 = 3, = 4
且 1 1 = 5,则异面直线 1与 的夹角余弦值为______.
三、解答题:本题共 5 小题,共 60 分。解答应写出文字说明,证明过程或演算步骤。
14.(本小题12分)
如图,在四面体 中, = 8, = 6, 、 分别为 、 的中点,并且异面直线 与 所成的
角为90°.求 的长.
15.(本小题12分)
如图,在四棱锥 中, // ,且∠ = ∠ = 90°.
(1)证明:平面 ⊥平面 ;
8
(2)若 = = = ,∠ = 90°,且四棱锥 的体积为 ,
3
求 与平面 所成的线面角的大小.
16.(本小题12分)
如图, 是圆柱 1的一条母线, 是底面的一条直径, 是圆 上一点,且 = = 5, = 3.
第 3 页,共 8 页
(1)求直线 与平面 所成角的大小;
(2)求点 到平面 的距离.
17.(本小题12分)
水果分为一级果和二级果,共136箱,其中一级果102箱,二级果34箱.
(1)随机挑选两箱水果,求恰好一级果和二级果各一箱的概率;
(2)进行分层抽样,共抽8箱水果,求一级果和二级果各几箱;
(3)抽取若干箱水果,其中一级果共120个,单果质量平均数为303.45克,方差为603.46;二级果48个,单
果质量平均数为240.41克,方差为648.21;求168个水果的方差和平均数,并预估果园中单果的质量.
18.(本小题12分)
在四棱锥 中,底面 是矩形, ⊥平面 , = = 4, = 2,以 的中点 为球心、
为直径的球面交 于点 ,交 于点 .
(1)求证: ⊥平面 ;
(2)求直线 与平面 所成角的正弦值;
(3)求点 到平面 的距离.
第 4 页,共 8 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】相交或异面
5.【答案】10
6.【答案】0.8
7.【答案】8
8.【答案】6
9.【答案】90.5
10.【答案】①③
11.【答案】0.004
12.【答案】①②④
5
13.【答案】
12
14.【答案】解:取 中点 ,连接 , ,
又因为 = 8, = 6, , 分别为 , 的中点,
1 1
所以 // , = = 4, // , = = 3,
2 2
又因为异面直线 与 所成的角为90°,所以∠ = 90°,
所以 2 = 2 + 2 = 42 + 32 = 25,
所以 = 5.
15.【答案】证明:(1) ∵在四棱锥 中,∠ = ∠ = 90°,
∴ ⊥ , ⊥ ,
又∵ // ,
第 5 页,共 8 页
∴ ⊥ ,
∵ ∩ = ,
∴ ⊥平面 ,
∵ 平面 ,
∴平面 ⊥平面 ;
(2)解:取 中点 ,连结 ,
∵ = , 为 的中点,
∴ ⊥ ,
∴ ⊥平面 , 平面 ,
∴ ⊥ ,
∵ ∩ = ,
∴ ⊥底面 ,
设 = = = = ,
则 √ 2 = √ 2 + 2 = √ 2 , = ,
2
8
∵四棱锥 的体积为 , ⊥底面 ,
3
1 1 1 √ 2 1 8
∴ = × 四边形 × = × × × = × × √ 2 × =
3 = ,解得 = 2,
3 3 3 2 3 3
√ 2
= = √ 2,
2
∴ = √ 2 + 2 + 2 = √ 2 + 2 + 4 = 2√ 2,
∵ ⊥底面 ,
∴ ∠ 为 与平面 所成的角,
在 △ 中, √ 2 1sin∠ = = = ,
2√ 2 2
∴ ∠ = 30°,
故 与平面 所成的线面角为30°.
第 6 页,共 8 页
16.【答案】解:(1) ∵ ⊥平面 , 平面 ,
∴ ⊥ ,
∵ 是圆 的直径,
∴ ⊥ ,
又 平面 , 平面 , ∩ = ,
∴ ⊥平面 .
∴ ∠ 是 与平面 所成的角.
∵ = = 5,∴ = 5√ 2,
3√ 2
∴ sin∠ = = .
10
∴直线 与平面 所成角的大小为 3√ 2arcsin .
10
(2)过 作 ⊥ ,垂足为 ,
由(1)得 ⊥平面 , 平面 ,
∴平面 ⊥平面 ,
又平面 ∩平面 = , 平面 , ⊥ ,
∴ ⊥平面 .
∵ = √ 2 2 = 4,∴ = √ 2 + 2 = √ 41.
20√ 41
∴ = = .
41
即 到平面 的距离为20√ 41.
41
17.【答案】解:(1)古典概型:设 事件为恰好选到一级果和二级果各一箱,样本空间的样本点的个数 =
136×135
2136 = = 9180, 2
事件的样本点的公式 = 1 1102 34 = 3468,
3468 17
所以 ( ) = = = ;
9180 45
(2)因为一级果箱数:二级果箱数= 3:1,
所以8箱水果中有一级果抽取6箱,二级果抽取2箱;
(3)设一级果平均质量为 ,方差为 2 2 ,二级果质量为 ,方差为 ,总体样本平均质量为 平均值,方差为
2,
因为 = 303.45, = 240.41, 2 = 603.46, 2 = 648.21,
120 48
所以 = × 303.45+ × 240.41= 285.44克,
120+48 120+48
第 7 页,共 8 页
2 120 48 = × [603.46+ (303.45 285.44)2]+ × [648.21+ (240.41 285.44)2] = 1427.27克 2.
120+48 120+48
102 34
预估:平均质量为 + = 287.69克.
136 136
18.【答案】解:(1)证明:依题设知, 是所作球面的直径,则 ⊥ ,
∵ ⊥平面 ,
则 ⊥ ,
又 ⊥ , , 平面 , ∩ = ,
∴ ⊥平面 ,
又 平面 ,
则 ⊥ ,
又 ∩ = , , 平面 ,
∴ ⊥平面 ;
(2)由(1)知, ⊥ ,
又 = ,则 是 的中点,
则 = 2√ 2, = √ 2 + 2 = 2√ 3,
1
则 △ = = 2√ 6, 2
设 到平面 的距离为 ,
由 = 得2√ 6 = 8,
2√ 6
可求得 = ,
3
设直线 与平面 所成角的大小为 ,
√ 6
则 = = ;
3
(3)由已知求得 = 6,
易知 ⊥ ,
2 8
由 = 得 = = ,
3
5
∴ = ,
9
5
故 点到平面 的距离等于 点到平面 距离的 ,
9
又∵ 是 的中点,则 、 到平面 的距离相等,
5 10√ 6
由(2)可知所求距离为 = .
9 27
第 8 页,共 8 页
一、单选题:本题共 3 小题,每小题 5 分,共 15 分。在每小题给出的选项中,只有一项是符合题目要求的。
1.空间两条互相平行的直线指的是( )
A. 在空间没有公共点的两条直线
B. 分别在两个平面上的两条直线
C. 在两个不同的平面上且没有公共点的两条直线
D. 在同一平面上且没有公共点的两条直线
2.方程
2
16 =
5 5
16 的解集是( )
A. {1,3,5,7} B. {1,3,5} C. {3,5} D. {1,3}
3.祖暅,又名祖暅之,是我国南北朝时期的数学家、天文学家祖冲之的儿子.他在《级术》中提出“幂势既
同,则积不容异”的结论,其中“幂”是面积.“势”是高,意思就是:夹在两个平行平面间的两个几何体,
被平行于这两个平行平面的任一平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积
相等(如图①).这一原理主要应用于计算一些复杂几何体的体积,若某艺术品如图②所示,高为40 ,底面
为边长20 的正三角形挖去以底边为直径的圆(如图③),则该艺术品的体积为( )
1000 2000
A. (1000√ 3 ) 3 B. (2000√ 3 ) 3
3 3
2000√ 3 2000 3 1000√ 3 1000C. ( ) D. ( ) 3
3 9 3 9
二、填空题:本题共 10 小题,每小题 5 分,共 50 分。
4.空间中已知直线 ,直线 ,直线 ,若直线 //直线 ,直线 与直线 异面,则直线 与直线 的位置关系
是______.
2
5.在( + )5的二项展开式中, 3的系数是______(用数字作答).
6.甲、乙同时炮击一架敌机,已知甲击中敌机的概率为0.6,乙击中敌机的概率为0.5,敌机被击中的概率为
______.
第 1 页,共 8 页
7.球的表面积扩大为原来的4倍,它的体积扩大为原来的______ 倍.
8.甲、乙等五名社区志愿者被随机分配到 、 、 、 四个不同岗位服务,每个岗位至少有一名志愿者,则
甲、乙两人同时参加岗位 服务的排法有______种.
9.以下数据为参加数学竞赛决赛的15人的成绩(单位:分),分数从低到高依次:56,70,72,78,79,80,
81,83,84,86,88,90,91,94,98,则这15人成绩的第80百分位数是 .
10.有以下命题:
①若 = + ( , ∈ ),则 与 、 共面;
②若 与 、 共面,则 = + ( , ∈ );
③若 = + ( , ∈ ),则 、 、 、 共面;
④若 、 、 、 共面,则 = + ( , ∈ ).则所有真命题的序号为______.
11.如图是某班一次数学测试成绩的茎叶图(图中仅列出[50,60),[90,100)的数据)和频率分布直方图,则
= ______.
12.如图,在棱长为2的正方体 1 1 1 1中, 为线段 1 上的动点(不
含端点),则下列结论正确的是______.
①平面 1 1 ⊥平面 1 ;
② 1 ⊥ ;
③∠ 1的取值范围是[ , )2 ;
4
④三棱锥 1 1 的体积为定值 . 3
第 2 页,共 8 页
13.已知四棱柱 1 1 1 1底面 为平行四边形, 1 = 3, = 4
且 1 1 = 5,则异面直线 1与 的夹角余弦值为______.
三、解答题:本题共 5 小题,共 60 分。解答应写出文字说明,证明过程或演算步骤。
14.(本小题12分)
如图,在四面体 中, = 8, = 6, 、 分别为 、 的中点,并且异面直线 与 所成的
角为90°.求 的长.
15.(本小题12分)
如图,在四棱锥 中, // ,且∠ = ∠ = 90°.
(1)证明:平面 ⊥平面 ;
8
(2)若 = = = ,∠ = 90°,且四棱锥 的体积为 ,
3
求 与平面 所成的线面角的大小.
16.(本小题12分)
如图, 是圆柱 1的一条母线, 是底面的一条直径, 是圆 上一点,且 = = 5, = 3.
第 3 页,共 8 页
(1)求直线 与平面 所成角的大小;
(2)求点 到平面 的距离.
17.(本小题12分)
水果分为一级果和二级果,共136箱,其中一级果102箱,二级果34箱.
(1)随机挑选两箱水果,求恰好一级果和二级果各一箱的概率;
(2)进行分层抽样,共抽8箱水果,求一级果和二级果各几箱;
(3)抽取若干箱水果,其中一级果共120个,单果质量平均数为303.45克,方差为603.46;二级果48个,单
果质量平均数为240.41克,方差为648.21;求168个水果的方差和平均数,并预估果园中单果的质量.
18.(本小题12分)
在四棱锥 中,底面 是矩形, ⊥平面 , = = 4, = 2,以 的中点 为球心、
为直径的球面交 于点 ,交 于点 .
(1)求证: ⊥平面 ;
(2)求直线 与平面 所成角的正弦值;
(3)求点 到平面 的距离.
第 4 页,共 8 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】相交或异面
5.【答案】10
6.【答案】0.8
7.【答案】8
8.【答案】6
9.【答案】90.5
10.【答案】①③
11.【答案】0.004
12.【答案】①②④
5
13.【答案】
12
14.【答案】解:取 中点 ,连接 , ,
又因为 = 8, = 6, , 分别为 , 的中点,
1 1
所以 // , = = 4, // , = = 3,
2 2
又因为异面直线 与 所成的角为90°,所以∠ = 90°,
所以 2 = 2 + 2 = 42 + 32 = 25,
所以 = 5.
15.【答案】证明:(1) ∵在四棱锥 中,∠ = ∠ = 90°,
∴ ⊥ , ⊥ ,
又∵ // ,
第 5 页,共 8 页
∴ ⊥ ,
∵ ∩ = ,
∴ ⊥平面 ,
∵ 平面 ,
∴平面 ⊥平面 ;
(2)解:取 中点 ,连结 ,
∵ = , 为 的中点,
∴ ⊥ ,
∴ ⊥平面 , 平面 ,
∴ ⊥ ,
∵ ∩ = ,
∴ ⊥底面 ,
设 = = = = ,
则 √ 2 = √ 2 + 2 = √ 2 , = ,
2
8
∵四棱锥 的体积为 , ⊥底面 ,
3
1 1 1 √ 2 1 8
∴ = × 四边形 × = × × × = × × √ 2 × =
3 = ,解得 = 2,
3 3 3 2 3 3
√ 2
= = √ 2,
2
∴ = √ 2 + 2 + 2 = √ 2 + 2 + 4 = 2√ 2,
∵ ⊥底面 ,
∴ ∠ 为 与平面 所成的角,
在 △ 中, √ 2 1sin∠ = = = ,
2√ 2 2
∴ ∠ = 30°,
故 与平面 所成的线面角为30°.
第 6 页,共 8 页
16.【答案】解:(1) ∵ ⊥平面 , 平面 ,
∴ ⊥ ,
∵ 是圆 的直径,
∴ ⊥ ,
又 平面 , 平面 , ∩ = ,
∴ ⊥平面 .
∴ ∠ 是 与平面 所成的角.
∵ = = 5,∴ = 5√ 2,
3√ 2
∴ sin∠ = = .
10
∴直线 与平面 所成角的大小为 3√ 2arcsin .
10
(2)过 作 ⊥ ,垂足为 ,
由(1)得 ⊥平面 , 平面 ,
∴平面 ⊥平面 ,
又平面 ∩平面 = , 平面 , ⊥ ,
∴ ⊥平面 .
∵ = √ 2 2 = 4,∴ = √ 2 + 2 = √ 41.
20√ 41
∴ = = .
41
即 到平面 的距离为20√ 41.
41
17.【答案】解:(1)古典概型:设 事件为恰好选到一级果和二级果各一箱,样本空间的样本点的个数 =
136×135
2136 = = 9180, 2
事件的样本点的公式 = 1 1102 34 = 3468,
3468 17
所以 ( ) = = = ;
9180 45
(2)因为一级果箱数:二级果箱数= 3:1,
所以8箱水果中有一级果抽取6箱,二级果抽取2箱;
(3)设一级果平均质量为 ,方差为 2 2 ,二级果质量为 ,方差为 ,总体样本平均质量为 平均值,方差为
2,
因为 = 303.45, = 240.41, 2 = 603.46, 2 = 648.21,
120 48
所以 = × 303.45+ × 240.41= 285.44克,
120+48 120+48
第 7 页,共 8 页
2 120 48 = × [603.46+ (303.45 285.44)2]+ × [648.21+ (240.41 285.44)2] = 1427.27克 2.
120+48 120+48
102 34
预估:平均质量为 + = 287.69克.
136 136
18.【答案】解:(1)证明:依题设知, 是所作球面的直径,则 ⊥ ,
∵ ⊥平面 ,
则 ⊥ ,
又 ⊥ , , 平面 , ∩ = ,
∴ ⊥平面 ,
又 平面 ,
则 ⊥ ,
又 ∩ = , , 平面 ,
∴ ⊥平面 ;
(2)由(1)知, ⊥ ,
又 = ,则 是 的中点,
则 = 2√ 2, = √ 2 + 2 = 2√ 3,
1
则 △ = = 2√ 6, 2
设 到平面 的距离为 ,
由 = 得2√ 6 = 8,
2√ 6
可求得 = ,
3
设直线 与平面 所成角的大小为 ,
√ 6
则 = = ;
3
(3)由已知求得 = 6,
易知 ⊥ ,
2 8
由 = 得 = = ,
3
5
∴ = ,
9
5
故 点到平面 的距离等于 点到平面 距离的 ,
9
又∵ 是 的中点,则 、 到平面 的距离相等,
5 10√ 6
由(2)可知所求距离为 = .
9 27
第 8 页,共 8 页
同课章节目录
