6.2.3 组合 课件(共19张PPT)
文档属性
| 名称 | 6.2.3 组合 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 15:07:34 | ||
图片预览





文档简介
(共19张PPT)
6.2.3 组合
学习目标
1. 理解组合、组合数的概念及组合和排列之间的区别与联系.
2. 能利用计数原理推导组合数公式,并熟练掌握组合数公式
及组合数的性质,能运用组合数的性质化简、计算、证明.
3. 能运用排列数公式、组合数公式和计数原理解决一些简单的
应用问题,提高数学应用能力和分析问题、解决问题的 能力.
新知引入
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).
1.排列的定义
我们把从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号 表示.
2.排列数的定义
3.排列数的计算
(1)排列数公式(1):
(2)全排列数:
(3)排列数公式(2):
新知引入
问题1:这两个问题有何不同?
甲乙、乙甲、甲丙、丙甲、乙丙、丙乙,共有=6种.
甲乙、甲丙、乙丙,共有3种.
问题2 从甲、乙、丙3名同学中选出2名去参加某天一项活动,有多少种不同的选法?
问题1 从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
将具体问题背景舍去,上述问题可以概括为:
从已知的3个不同元素中每次取出2个元素,按照一定的顺序排成一列.
从已知的3个不同元素中每次取出2个元素合成一组
排列问题
组合问题
组合与元素顺序无关
排列与元素顺序有关
这里每一组与顺序无关,我们把这种问题称为组合问题.
新知引入
新知学习
一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
1.组合定义:
注意:
(1)组合的特点:组合要求n个元素是不同的,取出的m个元素也是不同的,即从n个不同的元素中进行m次不放回地取出.
(2)组合的特性:元素的无序性. 取出的m个元素不讲究顺序,即元素没有位置的要求.
问题2:你能说一说排列与组合之间的联系与区别吗?
新知引入
新知学习
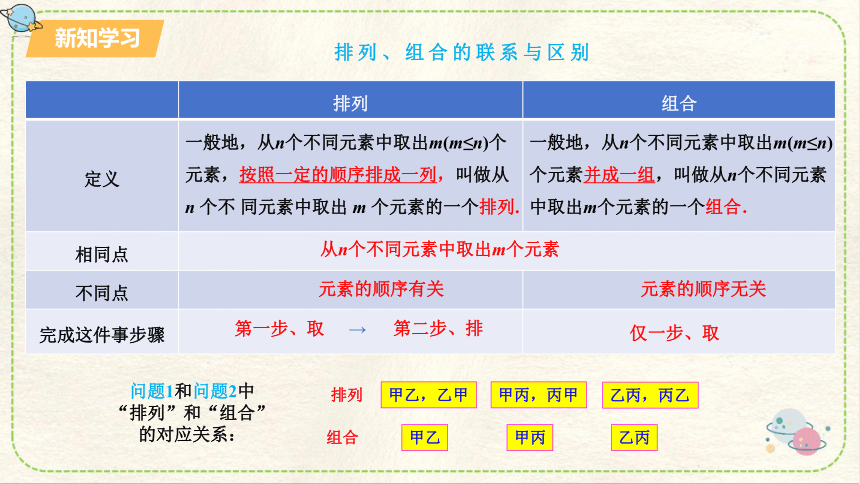
排列 组合
定义 一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从 n 个不 同元素中取出 m 个元素的一个排列. 一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
相同点 不同点
完成这件事步骤
从n个不同元素中取出m个元素
元素的顺序有关
元素的顺序无关
第一步、取
→ 第二步、排
仅一步、取
组合
甲乙
甲丙
乙丙
甲乙,乙甲
甲丙,丙甲
乙丙,丙乙
排列
问题1和问题2中“排列”和“组合”的对应关系:
排列、组合的联系与区别
新知引入
新知学习
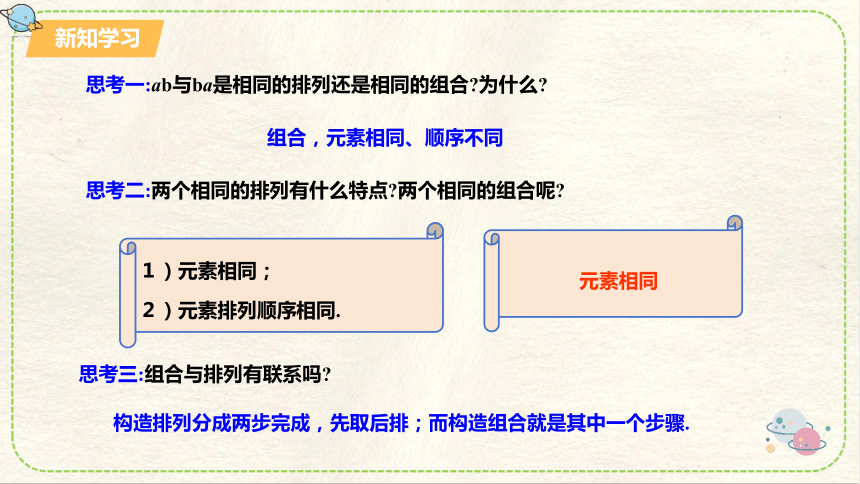
思考一:ab与ba是相同的排列还是相同的组合 为什么
思考二:两个相同的排列有什么特点 两个相同的组合呢
1)元素相同;
2)元素排列顺序相同.
元素相同
构造排列分成两步完成,先取后排;而构造组合就是其中一个步骤.
思考三:组合与排列有联系吗
组合,元素相同、顺序不同
练一练
(1) 设集合A={a,b,c,d,e},则集合A的含有3个元素的子集有多少个
(2) 某铁路线上有6个车站,则这条铁路线上共需准备多少种车票
有多少种不同的火车票价?
(3) 4名同学分成人数相同的舞蹈和书法两个课外小组,共有多少种分法
(4) 5人聚会,见面后每两人之间要握手相互问候,共需握手多少次
(5) 从3个风景点中选出2个游览,有多少种不同的方法
(6)从4个风景点中选出2个,分别在上午和下午去游览,有多少种不同的游览方法
1.判断下列问题是组合问题还是排列问题
(7).校门口停放着9辆共享自行车,其中黄色、红色、绿色的各3辆.
①从中选3辆,有多少种不同的方法 ②从中选3辆给3位同学,有多少种不同的方法
排列问题
组合问题
组合问题
组合问题
排列问题
组合问题
组合是选择的结果,排列是选择后再排序的结果.
组合问题
排列问题
组合问题
练一练
(1) 设集合A={a,b,c,d,e},则集合A的含有3个元素的子集有多少个
(2) 某铁路线上有6个车站,则这条铁路线共上有多少种不同的火车票价?
(3) 4名同学分成人数相同的舞蹈和书法两个课外小组,共有多少种分法
2.写出下列问题中所有不同的组合种数
{a,b,c},{a,b,d},{a,b,e},{a,c,d},{a,c,e},{a,d,e},{b,c,d},{b,c,e},{b,d,e},{c,d,e}共10种
设6个车站为A,B,C,D,E,F,车票种数AB,AC,AD,AE,AF,BC,BD,BE,BF,CD,CE,CF,DE,DF,EF共15种
设4名同学为A,B,C,D,选择舞蹈的同学组合有AB,AC,AD,BC,BD,CD,共6种,剩下的两名同学选书法
新知学习
典例解析
平面内有A,B,C,D共4个点.
(1) 以其中2个点为端点的有向线段共有多少条
(2) 以其中2个点为端点的线段共有多少条
例1
平面内有A,B,C,D共4个点.
(1) 以其中2个点为端点的有向线段共有多少条
(2) 以其中2个点为端点的线段共有多少条
思路点拨
在 (1)确定一条有向线段,不仅要确定两个端点,还要考虑它们的顺序,是排列问题;
(2)确定一条线段,只需确定两个端点,而不需考虑它们的顺序,是组合问题
新知学习
典例解析
平面内有A,B,C,D共4个点.
(1) 以其中2个点为端点的有向线段共有多少条
(2) 以其中2个点为端点的线段共有多少条
例1
平面内有A,B,C,D共4个点.
(1) 以其中2个点为端点的有向线段共有多少条
(2) 以其中2个点为端点的线段共有多少条
解:(1)一条有向线段的端点要分起点和端点,以平面内4个 点中的两个点为端点的有向线段的条数,就是从4个元素中取出2个元素的排列数,共有 条.
(2) 将(1)中端点相同、方向不同的2条有向线段作为1条线段,就是以平面内4个点中的2个点为端点的线段的条数, 共有如下6条:AB, AC, AD, BC, BD, CD.
这12条有向线段分别为
结论:取出2个元素的组合的个数是排列数的一半.
合作交流
问题:利用排列和组合之间的关系,以“元素相同”为标准分类,你能建立起例5(1)中排列和(2)中组合之间的对应关系吗?
进一步地,能否从这种对应关系出发,由排列数求出组合的个数
新知学习
练习1
1. 甲、乙、丙、丁4支足球队举行单循环赛.
(1) 列出所有各场比赛的双方;
(2) 列出所有冠、亚军的可能情况.
解:(1) 甲乙 甲丙 甲丁 乙丙 乙丁 丙丁.
(2)
冠军 甲 甲 甲 乙 乙 乙 丙 丙 丙 丁 丁 丁
亚军 乙 丙 丁 甲 丙 丁 甲 乙 丁 甲 乙 丙
随堂练习
解:△ABC,△ABD,△ACD,△BCD 共4个.
1. 已知平面内A, B, C, D这4个点中任何3个点都不在一条直线上,写出以其中任意3个点为顶点的所有三角形.
2. 现有1, 3, 7, 13这4个数.
(1) 从这4个数中任取2个相加,可以得到多少个不相等的和
(2) 从这4个数中任取2个相减,可以得到多少个不相等的差
解:(1) 不相等的和为4, 8, 14, 10, 16, 20,共6个.
(2) 不相等的差为-2, -6, -12, 2, -4, -10, 6, 4, 12, 10,共10个.
随堂练习
3.按下列条件,从甲、乙、丙、丁、戊、戌6人中选出3人,有多少种不同选法?
(1)甲、乙二人必须当选; (2)甲、乙二人不能当选;
(3)甲必须当选,乙不能当选; (4)甲、乙二人中只有一人当选;
解:(1) 从剩下的4人中选出1人,有丙、丁,戊,戌共4种结果.
(2) 从剩下的4人中选出3人,有丙丁戊、丙丁戌,丙戊戌,丁戊戌共4种结果.
(3) 从除甲乙之外剩下的4人中选出2人,有丙丁、丙戊,丙戌,丁戊,丁戌,戊戌共6种结果.
随堂练习
3.按下列条件,从甲、乙、丙、丁、戊、戌6人中选出3人,有多少种不同选法?
(1)甲、乙二人必须当选; (2)甲、乙二人不能当选;
(3)甲必须当选,乙不能当选; (4)甲、乙二人中只有一人当选;
(4)分两类情况:
第一类情况 甲当选乙没有当选,从除甲乙之外剩下的4人中选出2人,有丙丁、丙戊,丙戌,丁戊,丁戌,戊戌共6种结果,
第二类情况 乙当选甲没有当选,从除甲乙之外剩下的4人中选出2人,有丙丁、丙戊,丙戌,丁戊,丁戌,戊戌共6种结果,
由分类加法计数原理,共有6+6=12种.
课堂小结
一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
1.组合定义:
2.判断一个计数问题是排列问题还是组合问题的方法:
排列问题
组合问题
若交换某两个元素的位置对结果有影响,则是排列问题,即排列问题与选取的顺序有关.
若交换任意两个元素的位置对结果没有影响,则是组合问题,即组合问题与选取的顺序无关.
(1)判断是否为组合问题;(2)是否分类或分步;(3)根据组合的相关知识进行求解.
3.求一个组合问题的所有组合个数的基本方法:
课时作业
作业
1.《选择性必修第三册》P26“复习巩固” 4、7
2.“综合运用” 14,
*3.现有1,3,7,13这4个数.
(1)从这4个数中任取2个相加,可以得到多少个不相等的和
(2)从这4个数中任取2个相减,可以得到多少个不相等的差
拓展:校门口停放着9辆共享自行车,其中黄色、红色、绿色的各3辆.如何快速计算下列各问题?
①.从中选3辆,有多少种不同的方法 ②.从中选3辆给3位同学,有多少种不同的方法
课时作业
*3.现有1,3,7,13这4个数.
(1)从这4个数中任取2个相加,可以得到多少个不相等的和
(2)从这4个数中任取2个相减,可以得到多少个不相等的差
6.2.3 组合
学习目标
1. 理解组合、组合数的概念及组合和排列之间的区别与联系.
2. 能利用计数原理推导组合数公式,并熟练掌握组合数公式
及组合数的性质,能运用组合数的性质化简、计算、证明.
3. 能运用排列数公式、组合数公式和计数原理解决一些简单的
应用问题,提高数学应用能力和分析问题、解决问题的 能力.
新知引入
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).
1.排列的定义
我们把从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号 表示.
2.排列数的定义
3.排列数的计算
(1)排列数公式(1):
(2)全排列数:
(3)排列数公式(2):
新知引入
问题1:这两个问题有何不同?
甲乙、乙甲、甲丙、丙甲、乙丙、丙乙,共有=6种.
甲乙、甲丙、乙丙,共有3种.
问题2 从甲、乙、丙3名同学中选出2名去参加某天一项活动,有多少种不同的选法?
问题1 从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
将具体问题背景舍去,上述问题可以概括为:
从已知的3个不同元素中每次取出2个元素,按照一定的顺序排成一列.
从已知的3个不同元素中每次取出2个元素合成一组
排列问题
组合问题
组合与元素顺序无关
排列与元素顺序有关
这里每一组与顺序无关,我们把这种问题称为组合问题.
新知引入
新知学习
一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
1.组合定义:
注意:
(1)组合的特点:组合要求n个元素是不同的,取出的m个元素也是不同的,即从n个不同的元素中进行m次不放回地取出.
(2)组合的特性:元素的无序性. 取出的m个元素不讲究顺序,即元素没有位置的要求.
问题2:你能说一说排列与组合之间的联系与区别吗?
新知引入
新知学习
排列 组合
定义 一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从 n 个不 同元素中取出 m 个元素的一个排列. 一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
相同点 不同点
完成这件事步骤
从n个不同元素中取出m个元素
元素的顺序有关
元素的顺序无关
第一步、取
→ 第二步、排
仅一步、取
组合
甲乙
甲丙
乙丙
甲乙,乙甲
甲丙,丙甲
乙丙,丙乙
排列
问题1和问题2中“排列”和“组合”的对应关系:
排列、组合的联系与区别
新知引入
新知学习
思考一:ab与ba是相同的排列还是相同的组合 为什么
思考二:两个相同的排列有什么特点 两个相同的组合呢
1)元素相同;
2)元素排列顺序相同.
元素相同
构造排列分成两步完成,先取后排;而构造组合就是其中一个步骤.
思考三:组合与排列有联系吗
组合,元素相同、顺序不同
练一练
(1) 设集合A={a,b,c,d,e},则集合A的含有3个元素的子集有多少个
(2) 某铁路线上有6个车站,则这条铁路线上共需准备多少种车票
有多少种不同的火车票价?
(3) 4名同学分成人数相同的舞蹈和书法两个课外小组,共有多少种分法
(4) 5人聚会,见面后每两人之间要握手相互问候,共需握手多少次
(5) 从3个风景点中选出2个游览,有多少种不同的方法
(6)从4个风景点中选出2个,分别在上午和下午去游览,有多少种不同的游览方法
1.判断下列问题是组合问题还是排列问题
(7).校门口停放着9辆共享自行车,其中黄色、红色、绿色的各3辆.
①从中选3辆,有多少种不同的方法 ②从中选3辆给3位同学,有多少种不同的方法
排列问题
组合问题
组合问题
组合问题
排列问题
组合问题
组合是选择的结果,排列是选择后再排序的结果.
组合问题
排列问题
组合问题
练一练
(1) 设集合A={a,b,c,d,e},则集合A的含有3个元素的子集有多少个
(2) 某铁路线上有6个车站,则这条铁路线共上有多少种不同的火车票价?
(3) 4名同学分成人数相同的舞蹈和书法两个课外小组,共有多少种分法
2.写出下列问题中所有不同的组合种数
{a,b,c},{a,b,d},{a,b,e},{a,c,d},{a,c,e},{a,d,e},{b,c,d},{b,c,e},{b,d,e},{c,d,e}共10种
设6个车站为A,B,C,D,E,F,车票种数AB,AC,AD,AE,AF,BC,BD,BE,BF,CD,CE,CF,DE,DF,EF共15种
设4名同学为A,B,C,D,选择舞蹈的同学组合有AB,AC,AD,BC,BD,CD,共6种,剩下的两名同学选书法
新知学习
典例解析
平面内有A,B,C,D共4个点.
(1) 以其中2个点为端点的有向线段共有多少条
(2) 以其中2个点为端点的线段共有多少条
例1
平面内有A,B,C,D共4个点.
(1) 以其中2个点为端点的有向线段共有多少条
(2) 以其中2个点为端点的线段共有多少条
思路点拨
在 (1)确定一条有向线段,不仅要确定两个端点,还要考虑它们的顺序,是排列问题;
(2)确定一条线段,只需确定两个端点,而不需考虑它们的顺序,是组合问题
新知学习
典例解析
平面内有A,B,C,D共4个点.
(1) 以其中2个点为端点的有向线段共有多少条
(2) 以其中2个点为端点的线段共有多少条
例1
平面内有A,B,C,D共4个点.
(1) 以其中2个点为端点的有向线段共有多少条
(2) 以其中2个点为端点的线段共有多少条
解:(1)一条有向线段的端点要分起点和端点,以平面内4个 点中的两个点为端点的有向线段的条数,就是从4个元素中取出2个元素的排列数,共有 条.
(2) 将(1)中端点相同、方向不同的2条有向线段作为1条线段,就是以平面内4个点中的2个点为端点的线段的条数, 共有如下6条:AB, AC, AD, BC, BD, CD.
这12条有向线段分别为
结论:取出2个元素的组合的个数是排列数的一半.
合作交流
问题:利用排列和组合之间的关系,以“元素相同”为标准分类,你能建立起例5(1)中排列和(2)中组合之间的对应关系吗?
进一步地,能否从这种对应关系出发,由排列数求出组合的个数
新知学习
练习1
1. 甲、乙、丙、丁4支足球队举行单循环赛.
(1) 列出所有各场比赛的双方;
(2) 列出所有冠、亚军的可能情况.
解:(1) 甲乙 甲丙 甲丁 乙丙 乙丁 丙丁.
(2)
冠军 甲 甲 甲 乙 乙 乙 丙 丙 丙 丁 丁 丁
亚军 乙 丙 丁 甲 丙 丁 甲 乙 丁 甲 乙 丙
随堂练习
解:△ABC,△ABD,△ACD,△BCD 共4个.
1. 已知平面内A, B, C, D这4个点中任何3个点都不在一条直线上,写出以其中任意3个点为顶点的所有三角形.
2. 现有1, 3, 7, 13这4个数.
(1) 从这4个数中任取2个相加,可以得到多少个不相等的和
(2) 从这4个数中任取2个相减,可以得到多少个不相等的差
解:(1) 不相等的和为4, 8, 14, 10, 16, 20,共6个.
(2) 不相等的差为-2, -6, -12, 2, -4, -10, 6, 4, 12, 10,共10个.
随堂练习
3.按下列条件,从甲、乙、丙、丁、戊、戌6人中选出3人,有多少种不同选法?
(1)甲、乙二人必须当选; (2)甲、乙二人不能当选;
(3)甲必须当选,乙不能当选; (4)甲、乙二人中只有一人当选;
解:(1) 从剩下的4人中选出1人,有丙、丁,戊,戌共4种结果.
(2) 从剩下的4人中选出3人,有丙丁戊、丙丁戌,丙戊戌,丁戊戌共4种结果.
(3) 从除甲乙之外剩下的4人中选出2人,有丙丁、丙戊,丙戌,丁戊,丁戌,戊戌共6种结果.
随堂练习
3.按下列条件,从甲、乙、丙、丁、戊、戌6人中选出3人,有多少种不同选法?
(1)甲、乙二人必须当选; (2)甲、乙二人不能当选;
(3)甲必须当选,乙不能当选; (4)甲、乙二人中只有一人当选;
(4)分两类情况:
第一类情况 甲当选乙没有当选,从除甲乙之外剩下的4人中选出2人,有丙丁、丙戊,丙戌,丁戊,丁戌,戊戌共6种结果,
第二类情况 乙当选甲没有当选,从除甲乙之外剩下的4人中选出2人,有丙丁、丙戊,丙戌,丁戊,丁戌,戊戌共6种结果,
由分类加法计数原理,共有6+6=12种.
课堂小结
一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
1.组合定义:
2.判断一个计数问题是排列问题还是组合问题的方法:
排列问题
组合问题
若交换某两个元素的位置对结果有影响,则是排列问题,即排列问题与选取的顺序有关.
若交换任意两个元素的位置对结果没有影响,则是组合问题,即组合问题与选取的顺序无关.
(1)判断是否为组合问题;(2)是否分类或分步;(3)根据组合的相关知识进行求解.
3.求一个组合问题的所有组合个数的基本方法:
课时作业
作业
1.《选择性必修第三册》P26“复习巩固” 4、7
2.“综合运用” 14,
*3.现有1,3,7,13这4个数.
(1)从这4个数中任取2个相加,可以得到多少个不相等的和
(2)从这4个数中任取2个相减,可以得到多少个不相等的差
拓展:校门口停放着9辆共享自行车,其中黄色、红色、绿色的各3辆.如何快速计算下列各问题?
①.从中选3辆,有多少种不同的方法 ②.从中选3辆给3位同学,有多少种不同的方法
课时作业
*3.现有1,3,7,13这4个数.
(1)从这4个数中任取2个相加,可以得到多少个不相等的和
(2)从这4个数中任取2个相减,可以得到多少个不相等的差
