6.3.2 二项式系数的性质 课件(共19张PPT)
文档属性
| 名称 | 6.3.2 二项式系数的性质 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 15:09:16 | ||
图片预览





文档简介
(共19张PPT)
6.3.2 二项式系数的性质
第 六 章 计 数 原 理
1.会用二项式定理解决与二项展开式有关的简单问题.
2.理解二项式系数的性质并能进行简单运用.
1.二项式定理:
Tk+1=
2.二项展开式的通项:
3.二项式系数:
探究1 :用计算工具计算(a+b)n的展开式的二项式系数,并填入下表中.
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
n (a+b)n的展开式的二项式系数 1
2
3
4
5
6
杨辉三角形
二项式系数的性质
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
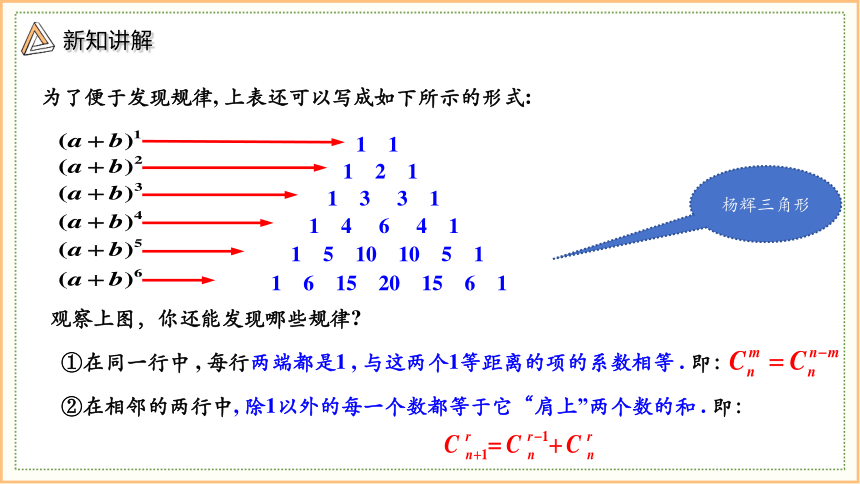
为了便于发现规律, 上表还可以写成如下所示的形式:
观察上图,你还能发现哪些规律
①在同一行中 , 每行两端都是1 , 与这两个1等距离的项的系数相等 . 即:
②在相邻的两行中, 除1以外的每一个数都等于它“肩上”两个数的和 . 即:
杨辉三角形
对于确定的n,我们还可以画出它的图像.
Cnr可看成是以r为自变量的函数f(r),其定义域是:
例如,当n=6 时,f(r)=Cnr (r∈{0, 1, 2, 3, 4, 5, 6})的图象是右图中的7个离散点.
f(r)
r
6
3
O
6
15
20
1
10
对于(a+b)n展开式的二项式系数:
还可以从函数角度来分析它们.
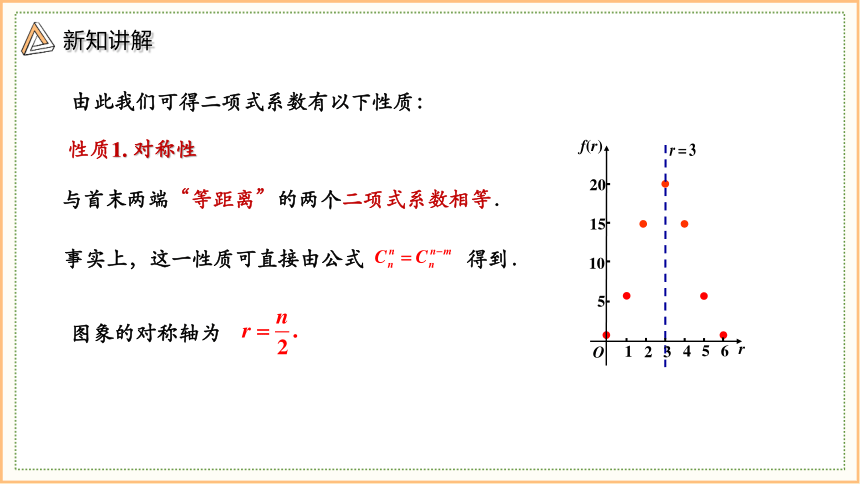
性质1. 对称性
由此我们可得二项式系数有以下性质:
与首末两端“等距离”的两个二项式系数相等.
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
事实上,这一性质可直接由公式 得到.
图象的对称轴为
性质2.增减性与最大值
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
探究2:已知 =
令x=1 得=
所以,的展开式的各二项式系数之和为2n
赋值法
性质3: 各二项式系数的和
各二项式系数的和
结论:
思考:
例1.求证:在的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
证明:在展开式=中,
令a=1,b=-1,得
即.
因此
即在的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
归纳总结
性质3: 各二项式系数的和
(1) ;
(2)
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1)二项展开式中系数最大的项与二项式系数最大的项是相同的.( )
×
(2)二项展开式的二项式系数和为
×
(3)在
×
(4)在
×
练一练:
.
;
2.填一填:
1024
练一练:
例2 (多选题)若 的展开式共有8项,则下列有关该二项展开式的说法
正确的是( )
BC
A. B.各二项式系数的和为128
C.二项式系数最大的项有2项 D.第4项与第5项的系数相等且最大
解:由题意可知,因为 的展开式共有8项,所以 ,所以A错误;
根据二项式系数和的性质,可得二项式系数的和为 ,所以B正确;
根据二项式系数的性质,可得中间项的二项式系数最大,即第4项和第5项的二项式系
数最大,所以C正确;
因为 的展开式的第4项为 ,第5项为
,所以展开式中第4项与第5项的系数不相等,所以D错误.
1.二项式系数最大的项的求法
求二项式系数最大的项,根据二项式系数的性质对 中的 进行讨论:
(1)当 为奇数时,中间两项的二项式系数最大;
(2)当 为偶数时,中间一项的二项式系数最大.
2.展开式中系数最大的项的求法:
求展开式中系数最大的项与求二项式系数最大的项是不同的,需要根据各项系数
的正、负变化情况进行分析.如求 的展开式中系数最大的项,一般
采用待定系数法.设展开式中各项系数分别为 , , , , ,且第 项
最大,应用 解出 ,即可得出系数最大的项.
方法归纳
3.在 的展开式中,
(1)求二项式系数最大的项.
(2)系数的绝对值最大的项是第几项?
(3)求系数最大的项与系数最小的项.
练一练:
解:
(1)二项式系数最大的项为中间项,即第5项,故 .
(2)设第 项系数的绝对值最大,
则 即 整理得 所以 或 .
故系数的绝对值最大的项是第6项和第7项.
(3)由(2)知,展开式中的第6项和第7项系数的绝对值最大,第6项的
系数为负,第7项的系数为正.
故系数最大的项为 ,
系数最小的项为 .
6.3.2 二项式系数的性质
第 六 章 计 数 原 理
1.会用二项式定理解决与二项展开式有关的简单问题.
2.理解二项式系数的性质并能进行简单运用.
1.二项式定理:
Tk+1=
2.二项展开式的通项:
3.二项式系数:
探究1 :用计算工具计算(a+b)n的展开式的二项式系数,并填入下表中.
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
n (a+b)n的展开式的二项式系数 1
2
3
4
5
6
杨辉三角形
二项式系数的性质
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
为了便于发现规律, 上表还可以写成如下所示的形式:
观察上图,你还能发现哪些规律
①在同一行中 , 每行两端都是1 , 与这两个1等距离的项的系数相等 . 即:
②在相邻的两行中, 除1以外的每一个数都等于它“肩上”两个数的和 . 即:
杨辉三角形
对于确定的n,我们还可以画出它的图像.
Cnr可看成是以r为自变量的函数f(r),其定义域是:
例如,当n=6 时,f(r)=Cnr (r∈{0, 1, 2, 3, 4, 5, 6})的图象是右图中的7个离散点.
f(r)
r
6
3
O
6
15
20
1
10
对于(a+b)n展开式的二项式系数:
还可以从函数角度来分析它们.
性质1. 对称性
由此我们可得二项式系数有以下性质:
与首末两端“等距离”的两个二项式系数相等.
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
事实上,这一性质可直接由公式 得到.
图象的对称轴为
性质2.增减性与最大值
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
探究2:已知 =
令x=1 得=
所以,的展开式的各二项式系数之和为2n
赋值法
性质3: 各二项式系数的和
各二项式系数的和
结论:
思考:
例1.求证:在的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
证明:在展开式=中,
令a=1,b=-1,得
即.
因此
即在的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
归纳总结
性质3: 各二项式系数的和
(1) ;
(2)
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1)二项展开式中系数最大的项与二项式系数最大的项是相同的.( )
×
(2)二项展开式的二项式系数和为
×
(3)在
×
(4)在
×
练一练:
.
;
2.填一填:
1024
练一练:
例2 (多选题)若 的展开式共有8项,则下列有关该二项展开式的说法
正确的是( )
BC
A. B.各二项式系数的和为128
C.二项式系数最大的项有2项 D.第4项与第5项的系数相等且最大
解:由题意可知,因为 的展开式共有8项,所以 ,所以A错误;
根据二项式系数和的性质,可得二项式系数的和为 ,所以B正确;
根据二项式系数的性质,可得中间项的二项式系数最大,即第4项和第5项的二项式系
数最大,所以C正确;
因为 的展开式的第4项为 ,第5项为
,所以展开式中第4项与第5项的系数不相等,所以D错误.
1.二项式系数最大的项的求法
求二项式系数最大的项,根据二项式系数的性质对 中的 进行讨论:
(1)当 为奇数时,中间两项的二项式系数最大;
(2)当 为偶数时,中间一项的二项式系数最大.
2.展开式中系数最大的项的求法:
求展开式中系数最大的项与求二项式系数最大的项是不同的,需要根据各项系数
的正、负变化情况进行分析.如求 的展开式中系数最大的项,一般
采用待定系数法.设展开式中各项系数分别为 , , , , ,且第 项
最大,应用 解出 ,即可得出系数最大的项.
方法归纳
3.在 的展开式中,
(1)求二项式系数最大的项.
(2)系数的绝对值最大的项是第几项?
(3)求系数最大的项与系数最小的项.
练一练:
解:
(1)二项式系数最大的项为中间项,即第5项,故 .
(2)设第 项系数的绝对值最大,
则 即 整理得 所以 或 .
故系数的绝对值最大的项是第6项和第7项.
(3)由(2)知,展开式中的第6项和第7项系数的绝对值最大,第6项的
系数为负,第7项的系数为正.
故系数最大的项为 ,
系数最小的项为 .
