第六章 平行四边形 评估测试卷(含答案) 2024-2025学年数学北师大版八年级下册
文档属性
| 名称 | 第六章 平行四边形 评估测试卷(含答案) 2024-2025学年数学北师大版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 251.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-22 00:00:00 | ||
图片预览


文档简介
第六章 平行四边形 评估测试卷
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024资阳中考)已知一个多边形的每个外角都等于60°,则该多边形的边数是 ( )
A.4 B.5 C.6 D.7
2.在平面直角坐标系中, ABCD的顶点A,B,C的坐标分别是(0,0),(3,0),(4,2),则顶点D的坐标为 ( )
A.(7,2) B.(5,4) C.(1,2) D.(2,1)
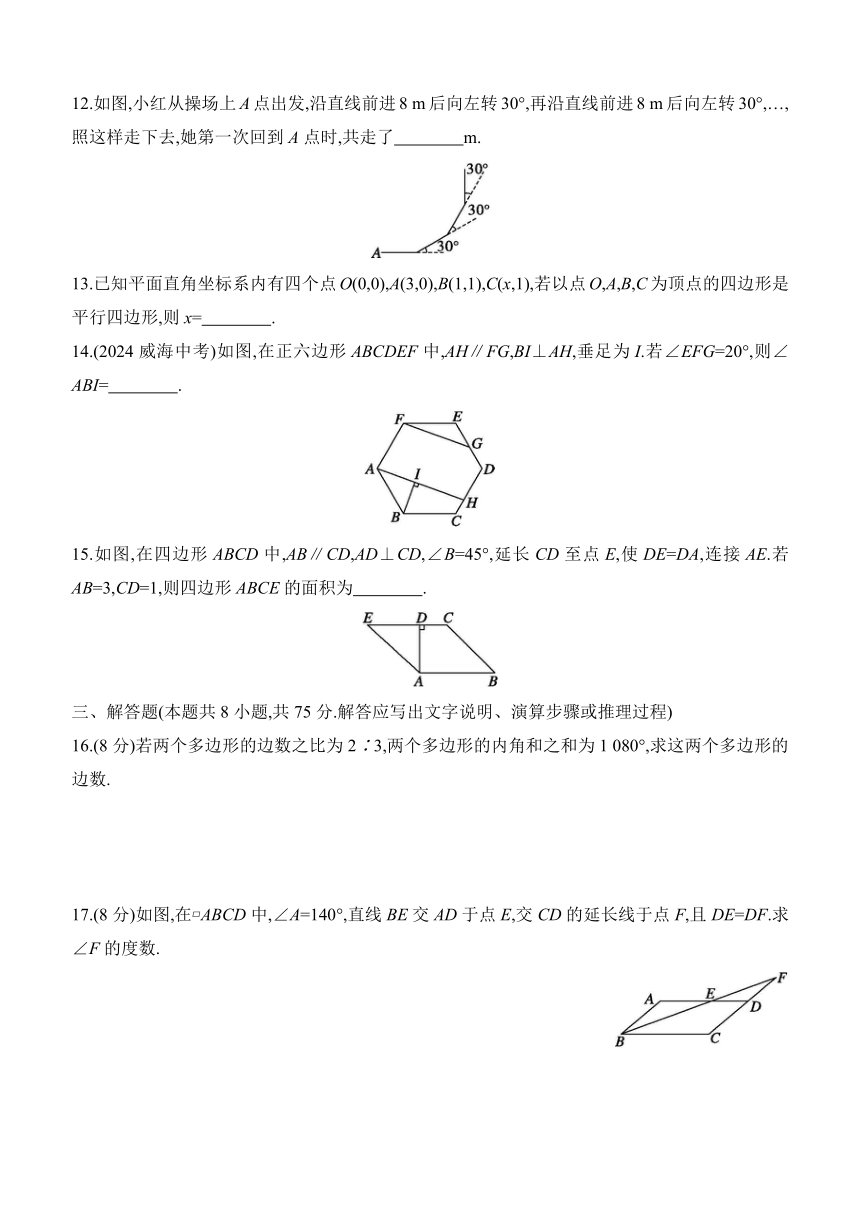
3.(2024辽宁中考)如图, ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD,若AC=3,BD=5,则四边形OCED的周长为 ( )
A.4 B.6 C.8 D.16
4.(2024广安中考)如图,在△ABC中,点D,E分别是AC,BC的中点,若∠A=45°,∠CED=70°,则∠C的度数为 ( )
A.45° B.50° C.60° D.65°
5.如图,在 ABCD中,AB=4,BC=6,对角线BD的垂直平分线交AD于点E,连接BE,则△ABE的周长是 ( )
A.7 B.8
C.9 D.10
6.如图,点E是 ABCD的一边AD上任意一点,若△EBC的面积为S1, ABCD的面积为S,则S与S1的关系是 ( )
A.S1=S B.S1C.S1>S D.无法确定
7.从五边形的一个顶点出发,共可以引出m条对角线,它们将五边形分成n个三角形,则m,n的值分别为 ( )
A.1,2 B.2,3
C.3,4 D.4,4
8.点A,B,C,D在同一平面内,从①AB∥CD,②AB=CD,③BC∥AD,④BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有 ( )
A.3种 B.4种 C.5种 D.6种
9.如图,四边形ABCD各边的中点分别是点E,F,G,H,若对角线AC,BD的长分别为9 cm和7 cm,则四边形EFGH的周长为 ( )
A.16 cm B.32 cm
C.24 cm D.18 cm
10.(2024眉山中考)如图,在 ABCD中,点O是BD的中点,EF过点O,下列结论:①AB∥DC;②EO=ED;③∠A=∠C;④S四边形ABOE=S四边形CDOF,其中正确结论的个数为 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共5小题,每小题3分,共15分)
11.如图,AB和CD是夹在两平行线l1,l2之间的平行线段,则AB CD.(填“>”“<”或“=”)
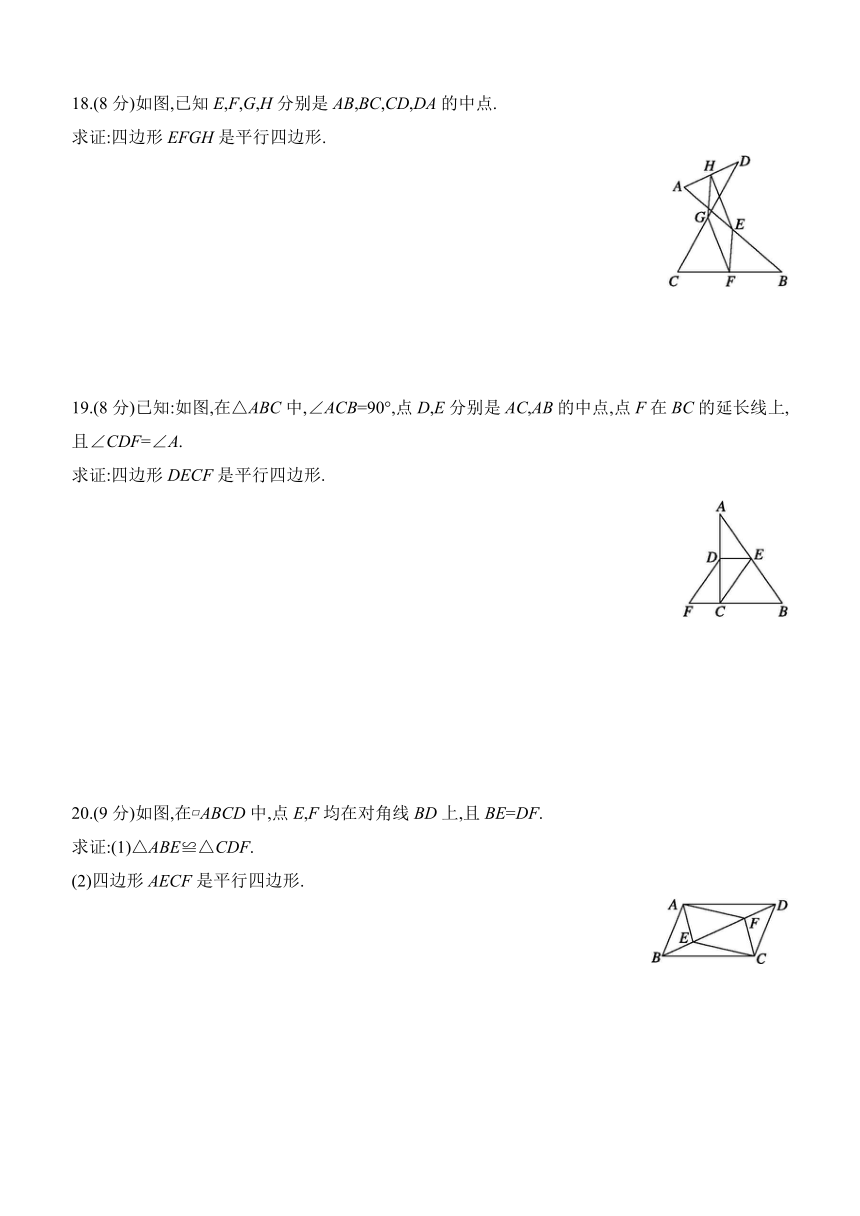
12.如图,小红从操场上A点出发,沿直线前进8 m后向左转30°,再沿直线前进8 m后向左转30°,…,照这样走下去,她第一次回到A点时,共走了 m.
13.已知平面直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以点O,A,B,C为顶点的四边形是平行四边形,则x= .
14.(2024威海中考)如图,在正六边形ABCDEF中,AH∥FG,BI⊥AH,垂足为I.若∠EFG=20°,则∠ABI= .
15.如图,在四边形ABCD中,AB∥CD,AD⊥CD,∠B=45°,延长CD至点E,使DE=DA,连接AE.若AB=3,CD=1,则四边形ABCE的面积为 .
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
16.(8分)若两个多边形的边数之比为2∶3,两个多边形的内角和之和为1 080°,求这两个多边形的边数.
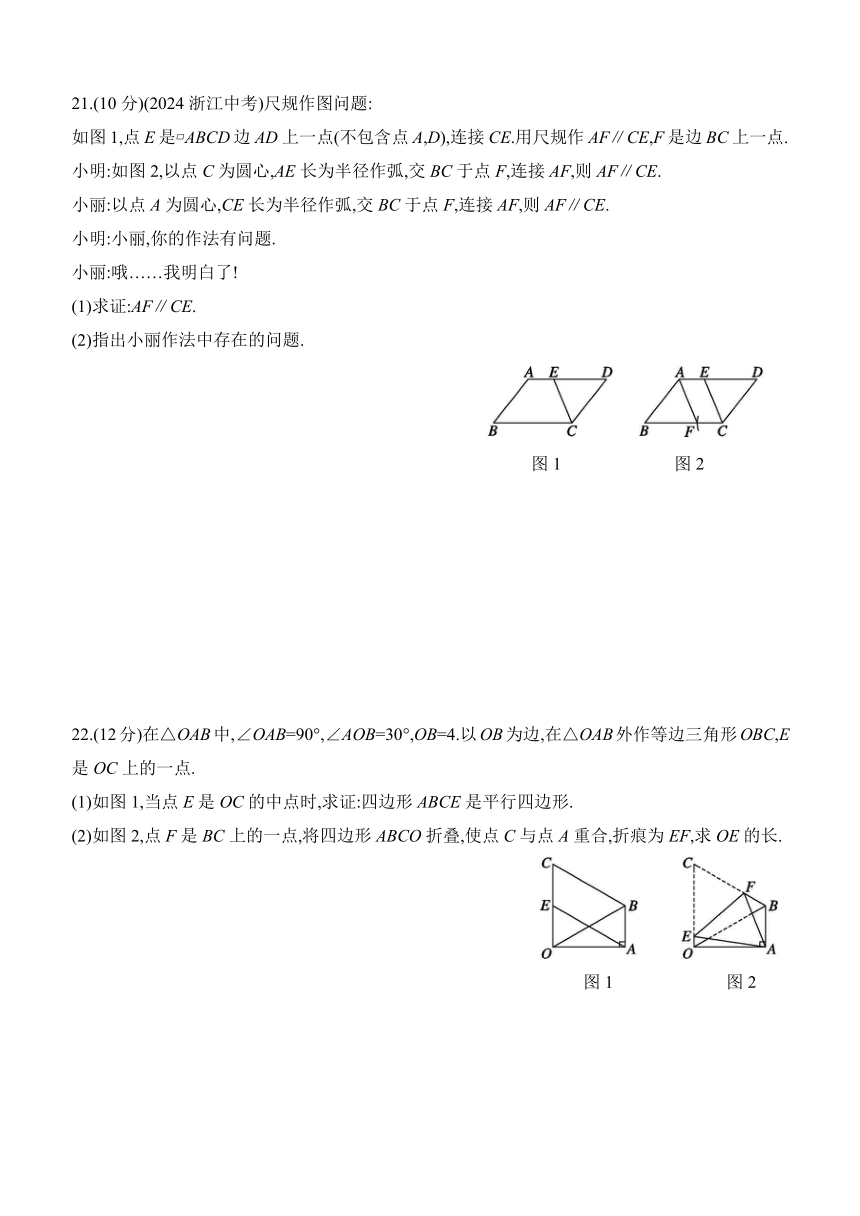
17.(8分)如图,在 ABCD中,∠A=140°,直线BE交AD于点E,交CD的延长线于点F,且DE=DF.求∠F的度数.
18.(8分)如图,已知E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
19.(8分)已知:如图,在△ABC中,∠ACB=90°,点D,E分别是AC,AB的中点,点F在BC的延长线上,且∠CDF=∠A.
求证:四边形DECF是平行四边形.
20.(9分)如图,在 ABCD中,点E,F均在对角线BD上,且BE=DF.
求证:(1)△ABE≌△CDF.
(2)四边形AECF是平行四边形.
21.(10分)(2024浙江中考)尺规作图问题:
如图1,点E是 ABCD边AD上一点(不包含点A,D),连接CE.用尺规作AF∥CE,F是边BC上一点.
小明:如图2,以点C为圆心,AE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小丽:以点A为圆心,CE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小明:小丽,你的作法有问题.
小丽:哦……我明白了!
(1)求证:AF∥CE.
(2)指出小丽作法中存在的问题.
图1 图2
22.(12分)在△OAB中,∠OAB=90°,∠AOB=30°,OB=4.以OB为边,在△OAB外作等边三角形OBC,E是OC上的一点.
(1)如图1,当点E是OC的中点时,求证:四边形ABCE是平行四边形.
(2)如图2,点F是BC上的一点,将四边形ABCO折叠,使点C与点A重合,折痕为EF,求OE的长.
图1 图2
23.(12分)如图,在 ABCD中,对角线AC,BD相交于点O,BD=10 cm,AC=14 cm.点E从点A出发沿AC向点C运动,点F从点C出发沿CA向点A运动,且两点都以每秒1 cm的速度同时出发.设运动时间为t s.
(1)当点E,F不与点O重合时,试证明四边形DEBF为平行四边形.
(2)在运动的过程中,∠EDF有可能为直角吗 若有可能,请直接写出t的值;若没有可能,请说明理由.
备用图
【详解答案】
1.C 解析:∵任意多边形的外角和都是360°,又∵这个多边形的每个外角都等于60°,∴该多边形的边数是360°÷60°=6.故选C.
2.C 解析:如图,∵四边形ABCD是平行四边形,∴CD=AB,CD∥AB.∵ ABCD的顶点A,B,C的坐标分别是(0,0),(3,0),(4,2),∴顶点D的坐标为(1,2).故选C.
3.C 解析:∵四边形ABCD是平行四边形,∴OC=AC=,OD=BD=.∵DE∥AC,CE∥BD,∴四边形OCED是平行四边形,∴四边形OCED的周长=2(OC+OD)=2×=8.故选C.
4.D 解析:∵点D,E分别是AC,BC的中点,∴DE是△ABC的中位线,∴DE∥AB,∴∠B=∠CED=70°,∴∠C=180°-∠A-∠B=180°-45°-70°=65°.故选D.
5.D 解析:∵BD的垂直平分线交AD于点E,∴BE=ED.∵四边形ABCD是平行四边形,∴AD=BC=6,∴△ABE的周长为AB+AE+BE=AB+AD=4+6=10.故选D.
6.A 解析:∵四边形ABCD是平行四边形,∴AD∥BC.设 ABCD的BC边上的高为h,则△EBC的面积S1=BC·h, ABCD的面积S=BC·h,∴S1=S.故选A.
7.B 解析:对角线的数量m=5-3=2(条);分成的三角形的数量n=5-2=3(个).故选B.
8.B 解析:∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形,∴选择①②,能使四边形ABCD是平行四边形;∵AB∥CD,BC∥AD,∴四边形ABCD是平行四边形,∴选择①③,能使四边形ABCD是平行四边形;∵AB=CD,BC=AD,∴四边形ABCD是平行四边形,∴选择②④,能使四边形ABCD是平行四边形;∵BC∥AD,BC=AD,∴四边形ABCD是平行四边形,∴选择③④,能使四边形ABCD是平行四边形;∵由AB∥CD,BC=AD不能确定四边形ABCD是平行四边形,∴选择①④不能使四边形ABCD是平行四边形;∵由AB=CD,BC∥AD不能确定四边形ABCD是平行四边形,∴选择②③不能使四边形ABCD是平行四边形.故选B.
9.A 解析:∵点E,F,G,H分别为AB,BC,CD,AD的中点,∴EF是△ABC的中位线,FG是△BCD的中位线,GH是△ADC的中位线,EH是△ABD的中位线,∴EF=AC=4.5 cm,FG=BD=3.5 cm,GH=AC=4.5 cm,EH=BD=3.5 cm,∴四边形EFGH的周长=EF+FG+GH+EH=4.5+3.5+4.5+3.5=16(cm).故选A.
10.C 解析:∵四边形ABCD是平行四边形,∴AB∥DC,AD∥BC,∠A=∠C,故①③正确,∴S△ABD=S△CDB=S ABCD,∠ODE=∠OBF.∵点O是BD的中点,∴OD=OB.又∵∠DOE=∠BOF,∴△ODE≌△OBF(ASA),∴S△ODE=S△OBF,EO=FO与ED不一定相等,故②不正确;∵S△ABD=S△CDB,S△ODE=S△OBF,∴S△ABD-S△ODE=S△CDB-S△OBF,即S四边形ABOE=S四边形CDOF,故④正确.综上所述,正确结论的个数为3个.故选C.
11.= 解析:∵l1∥l2,AB∥CD,∴四边形ABDC是平行四边形,∴AB=CD.
12.96 解析:∵360°÷30°=12,∴她需要走12个8 m才第一次回到A点,即一共走了8×12=96(m).
13.4或-2 解析:根据题意画图如下:
以点O,A,B,C为顶点的四边形是平行四边形,∴点C的坐标为(4,1)或(-2,1),∴x=4或-2.
14.50° 解析:∵六边形ABCDEF是正六边形,∴∠AFE=∠BAF==120°.∵∠EFG=20°,∴∠AFG=120°-20°=100°.∵AH∥FG,∴∠FAH=180°-100°=80°,∴∠BAI=120°-80°=40°.∵BI⊥AH,∴∠ABI=90°-40°=50°.
15.6 解析:∵AB∥CD,AD⊥CD,∠B=45°,∴∠C=135°,DA⊥DE.又∵DE=DA,∴∠E=45°,∴∠C+∠E=180°,∴AE∥BC.又∵CE∥AB,∴四边形ABCE是平行四边形,∴CE=AB=3,∴DA=DE=CE-CD=2,∴S ABCE=CE·AD=3×2=6.
16.解:设边数较少的多边形的边数为2n,则(2n-2)·180°+(3n-2)·180°=1 080°,
解得n=2.
∴2n=4,3n=6.
故这两个多边形的边数分别为4,6.
17.解:∵四边形ABCD为平行四边形,∠A=140°,
∴∠EDC=180°-∠A=40°.
又∵DE=DF,
∴∠EDC=2∠F=40°,
∴∠F=20°.
18.证明:如图,连接AC,
∵E,F,G,H分别是AB,BC,CD,DA的中点,
∴HG∥AC,HG=AC,EF∥AC,EF=AC,
∴HG∥EF,HG=EF,
∴四边形EFGH是平行四边形.
19.证明:∵点D,E分别为AC,AB的中点,
∴DE为△ACB的中位线.
∴DE∥BC.
∵CE为Rt△ACB斜边上的中线,
∴CE=AB=AE.
∴∠A=∠ACE.
又∵∠CDF=∠A,
∴∠CDF=∠ACE.
∴DF∥CE.
又∵DE∥BC,
∴四边形DECF是平行四边形.
20.证明:(1)∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB.
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS).
(2)由(1)可知,△ABE≌△CDF,
∴AE=CF,∠AEB=∠CFD,
∴180°-∠AEB=180°-∠CFD,
即∠AEF=∠CFE,
∴AE∥CF.
又∵AE=CF,
∴四边形AECF是平行四边形.
21.解:(1)证明:根据小明的作法知,CF=AE,
∵四边形ABCD是平行四边形,
∴AD∥BC.
又∵CF=AE,
∴四边形AFCE是平行四边形,
∴AF∥CE.
(2)以点A为圆心,CE长为半径作弧,交BC于点F,此时可能会有两个交点,只有其中之一符合题意.
故小丽的作法有问题.
22.解:(1)证明:∵△OBC为等边三角形,
∴OC=OB,∠COB=60°.
∵点E是OC的中点,
∴EC=OC=OB.
∵在△OAB中,∠OAB=90°,∠AOB=30°,
∴AB=OB,∠COA=90°,
∴CE=AB,∠COA+∠OAB=180°,
∴CE∥AB,
∴四边形ABCE是平行四边形.
(2)∵将四边形ABCO折叠,点C与点A重合,折痕为EF,
∴△CEF≌△AEF,
∴EC=EA.
∵OB=4,
∴OC=BC=4.
在△OAB中,∠OAB=90°,
∵∠AOB=30°,
∴AB=OB=2,
∴OA==2.
设OE=x,则AE=EC=4-x.
由(1)知∠EOA=90°,
∴在Rt△OAE中,OE2+OA2=AE2,
即x2+(2)2=(4-x)2,
解得x=,
∴OE=.
23.解:(1)证明:由题意得AE=CF=t cm.
如图1,当点E,F分别在OA,OC上时.
∵在 ABCD中,OB=OD,OA=OC,
又∵OE=OA-AE,OF=OC-CF,
∴OE=OF,
∴四边形DEBF为平行四边形.
如图2,当点E,F分别在OC,OA上时.
∵OE=AE-OA,OF=CF-OC,
∴OE=OF.
∵OB=OD,
∴四边形DEBF为平行四边形.
(2)当t=2或t=12时,∠EDF为直角.
解析:如图1,由(1)知OE=OF,OB=OD,要使∠EDF是直角,只需OE=OF=OD=BD=5 cm,则∠1=∠2,∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°,
∴∠2+∠3=90°.
即∠EDF=90°.
此时AE=CF=(AC-EF)=(14-10)=2(cm).
如图2,同理可得AE=CF=14-2=12(cm),
∴t=2或t=12.
图1
图2
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024资阳中考)已知一个多边形的每个外角都等于60°,则该多边形的边数是 ( )
A.4 B.5 C.6 D.7
2.在平面直角坐标系中, ABCD的顶点A,B,C的坐标分别是(0,0),(3,0),(4,2),则顶点D的坐标为 ( )
A.(7,2) B.(5,4) C.(1,2) D.(2,1)
3.(2024辽宁中考)如图, ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD,若AC=3,BD=5,则四边形OCED的周长为 ( )
A.4 B.6 C.8 D.16
4.(2024广安中考)如图,在△ABC中,点D,E分别是AC,BC的中点,若∠A=45°,∠CED=70°,则∠C的度数为 ( )
A.45° B.50° C.60° D.65°
5.如图,在 ABCD中,AB=4,BC=6,对角线BD的垂直平分线交AD于点E,连接BE,则△ABE的周长是 ( )
A.7 B.8
C.9 D.10
6.如图,点E是 ABCD的一边AD上任意一点,若△EBC的面积为S1, ABCD的面积为S,则S与S1的关系是 ( )
A.S1=S B.S1
7.从五边形的一个顶点出发,共可以引出m条对角线,它们将五边形分成n个三角形,则m,n的值分别为 ( )
A.1,2 B.2,3
C.3,4 D.4,4
8.点A,B,C,D在同一平面内,从①AB∥CD,②AB=CD,③BC∥AD,④BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有 ( )
A.3种 B.4种 C.5种 D.6种
9.如图,四边形ABCD各边的中点分别是点E,F,G,H,若对角线AC,BD的长分别为9 cm和7 cm,则四边形EFGH的周长为 ( )
A.16 cm B.32 cm
C.24 cm D.18 cm
10.(2024眉山中考)如图,在 ABCD中,点O是BD的中点,EF过点O,下列结论:①AB∥DC;②EO=ED;③∠A=∠C;④S四边形ABOE=S四边形CDOF,其中正确结论的个数为 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共5小题,每小题3分,共15分)
11.如图,AB和CD是夹在两平行线l1,l2之间的平行线段,则AB CD.(填“>”“<”或“=”)
12.如图,小红从操场上A点出发,沿直线前进8 m后向左转30°,再沿直线前进8 m后向左转30°,…,照这样走下去,她第一次回到A点时,共走了 m.
13.已知平面直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以点O,A,B,C为顶点的四边形是平行四边形,则x= .
14.(2024威海中考)如图,在正六边形ABCDEF中,AH∥FG,BI⊥AH,垂足为I.若∠EFG=20°,则∠ABI= .
15.如图,在四边形ABCD中,AB∥CD,AD⊥CD,∠B=45°,延长CD至点E,使DE=DA,连接AE.若AB=3,CD=1,则四边形ABCE的面积为 .
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
16.(8分)若两个多边形的边数之比为2∶3,两个多边形的内角和之和为1 080°,求这两个多边形的边数.
17.(8分)如图,在 ABCD中,∠A=140°,直线BE交AD于点E,交CD的延长线于点F,且DE=DF.求∠F的度数.
18.(8分)如图,已知E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
19.(8分)已知:如图,在△ABC中,∠ACB=90°,点D,E分别是AC,AB的中点,点F在BC的延长线上,且∠CDF=∠A.
求证:四边形DECF是平行四边形.
20.(9分)如图,在 ABCD中,点E,F均在对角线BD上,且BE=DF.
求证:(1)△ABE≌△CDF.
(2)四边形AECF是平行四边形.
21.(10分)(2024浙江中考)尺规作图问题:
如图1,点E是 ABCD边AD上一点(不包含点A,D),连接CE.用尺规作AF∥CE,F是边BC上一点.
小明:如图2,以点C为圆心,AE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小丽:以点A为圆心,CE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小明:小丽,你的作法有问题.
小丽:哦……我明白了!
(1)求证:AF∥CE.
(2)指出小丽作法中存在的问题.
图1 图2
22.(12分)在△OAB中,∠OAB=90°,∠AOB=30°,OB=4.以OB为边,在△OAB外作等边三角形OBC,E是OC上的一点.
(1)如图1,当点E是OC的中点时,求证:四边形ABCE是平行四边形.
(2)如图2,点F是BC上的一点,将四边形ABCO折叠,使点C与点A重合,折痕为EF,求OE的长.
图1 图2
23.(12分)如图,在 ABCD中,对角线AC,BD相交于点O,BD=10 cm,AC=14 cm.点E从点A出发沿AC向点C运动,点F从点C出发沿CA向点A运动,且两点都以每秒1 cm的速度同时出发.设运动时间为t s.
(1)当点E,F不与点O重合时,试证明四边形DEBF为平行四边形.
(2)在运动的过程中,∠EDF有可能为直角吗 若有可能,请直接写出t的值;若没有可能,请说明理由.
备用图
【详解答案】
1.C 解析:∵任意多边形的外角和都是360°,又∵这个多边形的每个外角都等于60°,∴该多边形的边数是360°÷60°=6.故选C.
2.C 解析:如图,∵四边形ABCD是平行四边形,∴CD=AB,CD∥AB.∵ ABCD的顶点A,B,C的坐标分别是(0,0),(3,0),(4,2),∴顶点D的坐标为(1,2).故选C.
3.C 解析:∵四边形ABCD是平行四边形,∴OC=AC=,OD=BD=.∵DE∥AC,CE∥BD,∴四边形OCED是平行四边形,∴四边形OCED的周长=2(OC+OD)=2×=8.故选C.
4.D 解析:∵点D,E分别是AC,BC的中点,∴DE是△ABC的中位线,∴DE∥AB,∴∠B=∠CED=70°,∴∠C=180°-∠A-∠B=180°-45°-70°=65°.故选D.
5.D 解析:∵BD的垂直平分线交AD于点E,∴BE=ED.∵四边形ABCD是平行四边形,∴AD=BC=6,∴△ABE的周长为AB+AE+BE=AB+AD=4+6=10.故选D.
6.A 解析:∵四边形ABCD是平行四边形,∴AD∥BC.设 ABCD的BC边上的高为h,则△EBC的面积S1=BC·h, ABCD的面积S=BC·h,∴S1=S.故选A.
7.B 解析:对角线的数量m=5-3=2(条);分成的三角形的数量n=5-2=3(个).故选B.
8.B 解析:∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形,∴选择①②,能使四边形ABCD是平行四边形;∵AB∥CD,BC∥AD,∴四边形ABCD是平行四边形,∴选择①③,能使四边形ABCD是平行四边形;∵AB=CD,BC=AD,∴四边形ABCD是平行四边形,∴选择②④,能使四边形ABCD是平行四边形;∵BC∥AD,BC=AD,∴四边形ABCD是平行四边形,∴选择③④,能使四边形ABCD是平行四边形;∵由AB∥CD,BC=AD不能确定四边形ABCD是平行四边形,∴选择①④不能使四边形ABCD是平行四边形;∵由AB=CD,BC∥AD不能确定四边形ABCD是平行四边形,∴选择②③不能使四边形ABCD是平行四边形.故选B.
9.A 解析:∵点E,F,G,H分别为AB,BC,CD,AD的中点,∴EF是△ABC的中位线,FG是△BCD的中位线,GH是△ADC的中位线,EH是△ABD的中位线,∴EF=AC=4.5 cm,FG=BD=3.5 cm,GH=AC=4.5 cm,EH=BD=3.5 cm,∴四边形EFGH的周长=EF+FG+GH+EH=4.5+3.5+4.5+3.5=16(cm).故选A.
10.C 解析:∵四边形ABCD是平行四边形,∴AB∥DC,AD∥BC,∠A=∠C,故①③正确,∴S△ABD=S△CDB=S ABCD,∠ODE=∠OBF.∵点O是BD的中点,∴OD=OB.又∵∠DOE=∠BOF,∴△ODE≌△OBF(ASA),∴S△ODE=S△OBF,EO=FO与ED不一定相等,故②不正确;∵S△ABD=S△CDB,S△ODE=S△OBF,∴S△ABD-S△ODE=S△CDB-S△OBF,即S四边形ABOE=S四边形CDOF,故④正确.综上所述,正确结论的个数为3个.故选C.
11.= 解析:∵l1∥l2,AB∥CD,∴四边形ABDC是平行四边形,∴AB=CD.
12.96 解析:∵360°÷30°=12,∴她需要走12个8 m才第一次回到A点,即一共走了8×12=96(m).
13.4或-2 解析:根据题意画图如下:
以点O,A,B,C为顶点的四边形是平行四边形,∴点C的坐标为(4,1)或(-2,1),∴x=4或-2.
14.50° 解析:∵六边形ABCDEF是正六边形,∴∠AFE=∠BAF==120°.∵∠EFG=20°,∴∠AFG=120°-20°=100°.∵AH∥FG,∴∠FAH=180°-100°=80°,∴∠BAI=120°-80°=40°.∵BI⊥AH,∴∠ABI=90°-40°=50°.
15.6 解析:∵AB∥CD,AD⊥CD,∠B=45°,∴∠C=135°,DA⊥DE.又∵DE=DA,∴∠E=45°,∴∠C+∠E=180°,∴AE∥BC.又∵CE∥AB,∴四边形ABCE是平行四边形,∴CE=AB=3,∴DA=DE=CE-CD=2,∴S ABCE=CE·AD=3×2=6.
16.解:设边数较少的多边形的边数为2n,则(2n-2)·180°+(3n-2)·180°=1 080°,
解得n=2.
∴2n=4,3n=6.
故这两个多边形的边数分别为4,6.
17.解:∵四边形ABCD为平行四边形,∠A=140°,
∴∠EDC=180°-∠A=40°.
又∵DE=DF,
∴∠EDC=2∠F=40°,
∴∠F=20°.
18.证明:如图,连接AC,
∵E,F,G,H分别是AB,BC,CD,DA的中点,
∴HG∥AC,HG=AC,EF∥AC,EF=AC,
∴HG∥EF,HG=EF,
∴四边形EFGH是平行四边形.
19.证明:∵点D,E分别为AC,AB的中点,
∴DE为△ACB的中位线.
∴DE∥BC.
∵CE为Rt△ACB斜边上的中线,
∴CE=AB=AE.
∴∠A=∠ACE.
又∵∠CDF=∠A,
∴∠CDF=∠ACE.
∴DF∥CE.
又∵DE∥BC,
∴四边形DECF是平行四边形.
20.证明:(1)∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB.
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS).
(2)由(1)可知,△ABE≌△CDF,
∴AE=CF,∠AEB=∠CFD,
∴180°-∠AEB=180°-∠CFD,
即∠AEF=∠CFE,
∴AE∥CF.
又∵AE=CF,
∴四边形AECF是平行四边形.
21.解:(1)证明:根据小明的作法知,CF=AE,
∵四边形ABCD是平行四边形,
∴AD∥BC.
又∵CF=AE,
∴四边形AFCE是平行四边形,
∴AF∥CE.
(2)以点A为圆心,CE长为半径作弧,交BC于点F,此时可能会有两个交点,只有其中之一符合题意.
故小丽的作法有问题.
22.解:(1)证明:∵△OBC为等边三角形,
∴OC=OB,∠COB=60°.
∵点E是OC的中点,
∴EC=OC=OB.
∵在△OAB中,∠OAB=90°,∠AOB=30°,
∴AB=OB,∠COA=90°,
∴CE=AB,∠COA+∠OAB=180°,
∴CE∥AB,
∴四边形ABCE是平行四边形.
(2)∵将四边形ABCO折叠,点C与点A重合,折痕为EF,
∴△CEF≌△AEF,
∴EC=EA.
∵OB=4,
∴OC=BC=4.
在△OAB中,∠OAB=90°,
∵∠AOB=30°,
∴AB=OB=2,
∴OA==2.
设OE=x,则AE=EC=4-x.
由(1)知∠EOA=90°,
∴在Rt△OAE中,OE2+OA2=AE2,
即x2+(2)2=(4-x)2,
解得x=,
∴OE=.
23.解:(1)证明:由题意得AE=CF=t cm.
如图1,当点E,F分别在OA,OC上时.
∵在 ABCD中,OB=OD,OA=OC,
又∵OE=OA-AE,OF=OC-CF,
∴OE=OF,
∴四边形DEBF为平行四边形.
如图2,当点E,F分别在OC,OA上时.
∵OE=AE-OA,OF=CF-OC,
∴OE=OF.
∵OB=OD,
∴四边形DEBF为平行四边形.
(2)当t=2或t=12时,∠EDF为直角.
解析:如图1,由(1)知OE=OF,OB=OD,要使∠EDF是直角,只需OE=OF=OD=BD=5 cm,则∠1=∠2,∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°,
∴∠2+∠3=90°.
即∠EDF=90°.
此时AE=CF=(AC-EF)=(14-10)=2(cm).
如图2,同理可得AE=CF=14-2=12(cm),
∴t=2或t=12.
图1
图2
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
