第三章 函数及其图象 第5节 二次函数的综合应用(含答案)
文档属性
| 名称 | 第三章 函数及其图象 第5节 二次函数的综合应用(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 10.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 15:14:42 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第三章 函数及其图象
第5节 二次函数的综合应用
考点分析
考点 1 抛物线型实际问题
课标要求导航:①通过对实际问题的分析,体会二次函数的意义;②能解决相应
的实际问题.
类型1 抛物线型建筑问题
例1 一条河上横跨着一座宏伟壮观的悬索桥.桥梁的缆索 与缆索 均呈抛物线型,桥塔AO 与桥塔BC 均垂直于桥面,如图所示,以O 为原点,以直线 为x轴,以桥塔AO 所在直线为y轴,建立平面直角坐标系.
已知:缆索 所在抛物线与缆索 所在抛物线关于y轴对称,桥塔AO与桥塔BC 之间的距离( 缆索 的最低点 P 到 的距离 .(桥塔的粗细忽略不计)
(1)求缆索. 所在抛物线的函数表达式;
(2)点E 在缆索 上, 且 求FO 的长.
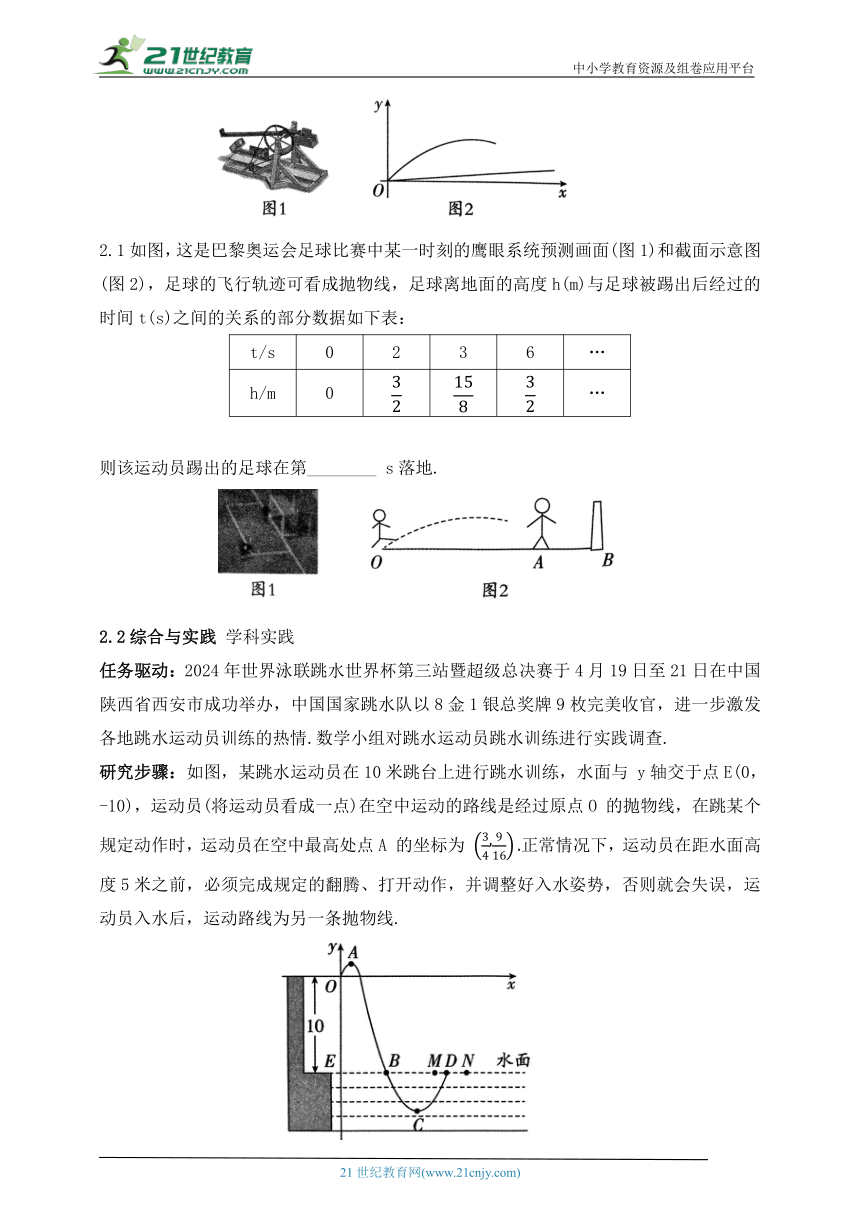
例2 传统文化 如图1 所示的某种发石车是古代一种远程攻击的武器.将发石车置于山坡底部O处,以点O为原点,水平方向为x轴方向,建立如图2所示的平面直角坐标系,将发射出去的石块当作一个点看,其飞行路线可以近似看作抛物线 的一部分,则发射石块在空中飞行的最大高度为_________米.
2.1如图,这是巴黎奥运会足球比赛中某一时刻的鹰眼系统预测画面(图1)和截面示意图(图2),足球的飞行轨迹可看成抛物线,足球离地面的高度h(m)与足球被踢出后经过的时间t(s)之间的关系的部分数据如下表:
t/s 0 2 3 6 …
h/m 0 …
则该运动员踢出的足球在第________ s落地.
2.2综合与实践 学科实践
任务驱动:2024年世界泳联跳水世界杯第三站暨超级总决赛于4月19日至21日在中国陕西省西安市成功举办,中国国家跳水队以8金1银总奖牌9枚完美收官,进一步激发各地跳水运动员训练的热情.数学小组对跳水运动员跳水训练进行实践调查.
研究步骤:如图,某跳水运动员在10米跳台上进行跳水训练,水面与 y轴交于点E(0,-10),运动员(将运动员看成一点)在空中运动的路线是经过原点O 的抛物线,在跳某个规定动作时,运动员在空中最高处点A 的坐标为 正常情况下,运动员在距水面高度5米之前,必须完成规定的翻腾、打开动作,并调整好入水姿势,否则就会失误,运动员入水后,运动路线为另一条抛物线.
问题解决:请根据上述研究步骤与相关数据,完成下列任务.
(1)求运动员在空中运动时对应抛物线的解析式及入水处点 B 的坐标;
(2)若运动员在空中调整好入水姿势时,恰好与y轴的水平距离为3米,问该运动员此次跳水会不会失误 说明理由;
(3)在该运动员入水处点B 的正前方有M,N两点,且. 8,该运动员入水后运动路线对应的抛物线的解析式为 .若该运动员出水处点D在MN之间(包括M,N两点),请求出k的取值范围.
考点2 利用二次函数的性质解决最优问题
课标要求导航:①通过对实际问题的分析,体会二次函数的意义;②能解决相应的实际问题.
例3 如图,小明的父亲想用长为60米的栅栏,再借助房屋的外墙围成一个矩形的菜园.已知房屋外墙长40 米,则可围成的菜园的最大面积是__________平方米.
例3题图 例4题图
例4 跨物理学科 某物理兴趣小组对一款饮水机的工作电路展开研究,如图1,将变阻器R 的滑片从一端滑到另一端,绘制出变阻器R 消耗的电功率P 随电流I变化的关系图象,如图2所示,且该图象是经过原点的一条抛物线的一部分,则变阻器R 消耗的电功率P 最大为 ( )
A.160 W B.180 W C.200 W D.220 W
例5 某商场以每件80元的价格购进一种商品,在一段时间内,销售量y(单位:件)与销售单价x(单位:元/件)之间是一次函数关系,其部分图象如图所示.
(1)求这段时间内y与x之间的函数解析式;
(2)在这段时间内,若销售单价不低于100元,且商场还要完成不少于220件的销售任务,当销售单价为多少时,商场获得利润最大 最大利润是多少
5.1 某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(盒)与销售单价x(元)是一次函数关系,下表是y与x的几组对应值.
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 … 56 52 48 44 40 …
(1)求y与x的函数表达式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
考点3 与几何有关的二次函数综合题(
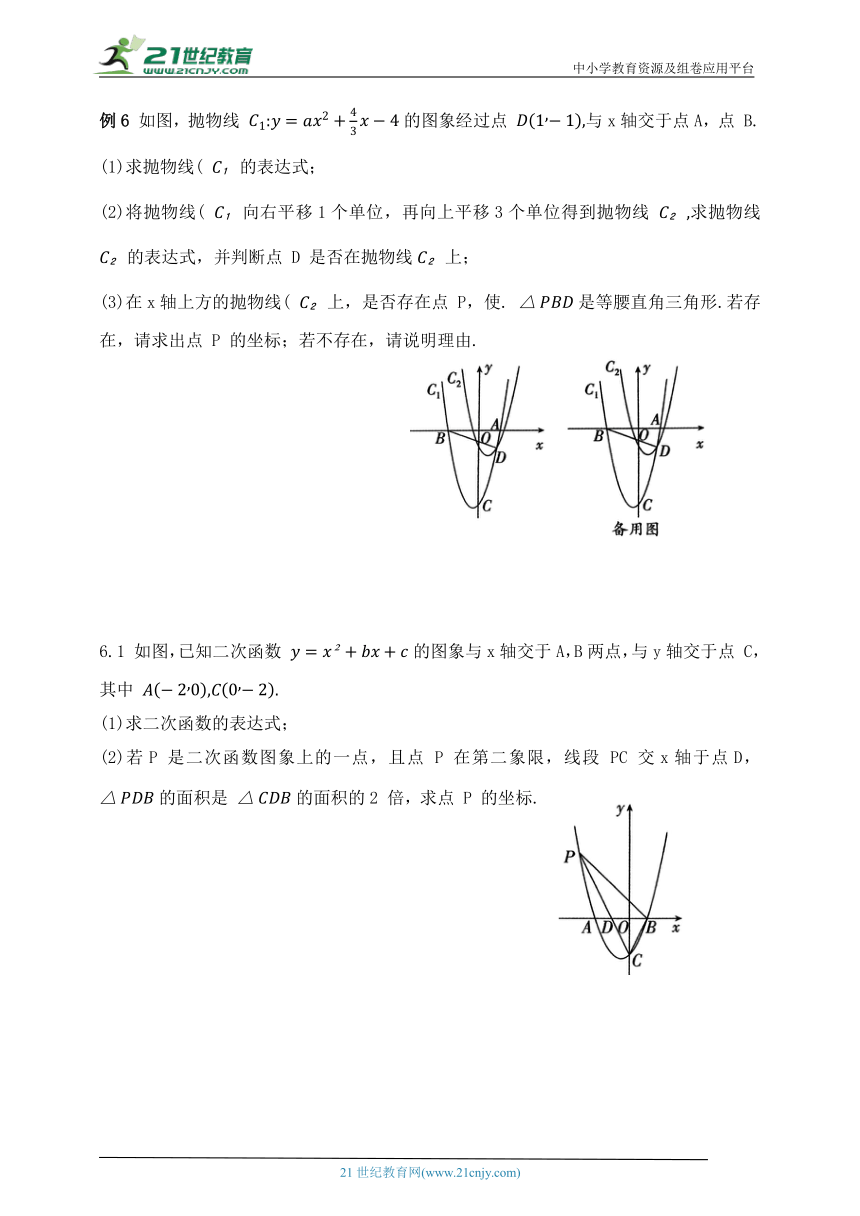
例6 如图,抛物线 的图象经过点 与x轴交于点A,点 B.
(1)求抛物线( 的表达式;
(2)将抛物线( 向右平移1个单位,再向上平移3个单位得到抛物线 求抛物线 的表达式,并判断点 D 是否在抛物线上;
(3)在x轴上方的抛物线( 上,是否存在点 P,使. 是等腰直角三角形.若存在,请求出点 P 的坐标;若不存在,请说明理由.
6.1 如图,已知二次函数 的图象与x轴交于A,B两点,与y轴交于点 C,其中
(1)求二次函数的表达式;
(2)若P 是二次函数图象上的一点,且点 P 在第二象限,线段 PC 交x轴于点D, 的面积是 的面积的2 倍,求点 P 的坐标.
达标训练
基础达标训练
1.一个球从地面竖直向上弹起时的速度为10米/秒,经过t(秒)时球距离地面的高度h(米)适用公式 那么球弹起后又回到地面所花的时间t(秒)是 ( )
A.5 B.10 C.1 D.2
2.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是 ≤t≤6).有下列结论:
①小球从抛出到落地需要6s;
②小球运动中的高度可以是30m;
③小球运动2 s时的高度小于运动5s 时的高度.
其中,正确结论的个数是 ( )
A.0 B.1 C.2 D.3
3.如图,壮壮同学投掷实心球,出手(点P 处)的高度OP 是 出手后实心球沿一段抛物线运行,到达最高点时,水平距离是5m ,高度是4m .若实心球落地点为M,则
4.真实问题情境 如图1为一汽车停车棚,其棚顶的横截面可以看作是抛物线的一部分,如图2 是棚顶的竖直高度y(单位:m)与距离停车棚支柱AO 的水平距离x(单位:m)近似满足函数关系 的图象,点B(6,2.68)在图象上.若一辆箱式货车需在停车棚下避雨,货车截面看作长高 的矩形,则可判定货车___________完全停到车棚内.(填“能”或“不能”)
5.广东省全力实施“百县千镇万村高质量发展工程”,2023 年农产品进出口总额居全国首位,其中荔枝鲜果远销欧美.某果商以每吨2万元的价格收购早熟荔枝,销往国外,若按每吨5万元出售,平均每天可售出100 吨.市场调查反映:如果每吨降价1万元,每天销售量相应增加50 吨.该果商如何定价才能使每天的“利润”或“销售收入”最大 并求出其最大值.(题中“元”为人民币)
高分提能训练
6.如图,正方形ABCD 的顶点A,C 在抛物线 上,点D 在y轴上.若A,C 两点的横坐标分别为下列结论正确的是 ( )
第6题图 第7题图
7.九(1)班劳动实践基地内有一块面积足够大的平整空地,地上两段围墙 于点O(如图),其中AB上的EO段围墙空缺.同学们测得 班长买来可切断的围栏 16 m,准备利用已有围墙,围出一块封闭的矩形菜地,则该菜地最大面积是__________
8.在校园科技节期间,科普员为同学们进行了水火箭的发射表演,图1是某型号水火箭的实物图,水火箭发射后的运动路线可以看作是一条抛物线.为了解水火箭的相关性能,同学们进一步展开研究.如图2 建立直角坐标系.水火箭发射后落在水平地面A处.科普员提供了该型号水火箭与地面成一定角度时,从发射到着陆过程中,水火箭距离地面OA 的竖直高度y(m)与离发射点 O 的水平距离x(m)的几组关系数据如下:
水平距离x(m) 0 3 4 10 15 20 22 27
竖直高度y(m) 0 3.24 4.16 8 9 8 7.04 3.24
(1)根据如表,请确定抛物线的表达式;
(2)请计算当水火箭飞行至离发射点O 的水平距离为5m 时,水火箭距离地面的竖直高度.
9.16世纪中叶,我国发明了一种新式火箭“火龙出水”,它是二级火箭的始祖.火箭第一级运行路径形如抛物线,当火箭运行一定水平距离时,自动引发火箭第二级,火箭第二级沿直线运行.
某科技小组运用信息技术模拟火箭运行过程.如图,以发射点为原点,地平线为x轴,垂直于地面的直线为 y 轴,建立平面直角坐标系,分别得到抛物线 和直线其中,当火箭运行的水平距离为9 km时,自动引发火箭的第二级.
(1)若火箭第二级的引发点的高度为3.6km,
①直接写出a,b的值;
②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低1.35 km,求这两个位置之间的距离.
(2)直接写出a满足什么条件时,火箭落地点与发射点的水平距离超过15 km.
冲刺满分训练
10.抛物线 与x轴交于 B两点,与y轴交于点C,点P 是第四象限内抛物线上的一点.
(1)求抛物线的解析式;
(2)如图1,过P作 轴于点D,交直线BC 于点 E.设点 D 的横坐标为m,当 时,求m 的值;
(3)如图2点 F(1,0),连接 CF 并延长交直线PD 于点 M,点N是x轴上方抛物线上的一点,在(2)的条件下,x轴上是否存在一点H,使得以F,M,N,H为顶点的四边形是平行四边形.若存在,直接写出点 H 的坐标;若不存在,请说明理由.
参考答案
【例1】解:(1)由题意,得A(0,17),抛物线的顶点 P 为(50,2).
故可设抛物线的函数表达式为
将A(0,17)代入,得 17,解得
∴缆索 所在抛物线的函数表达式为
(2)∵ 缆索. 所在抛物线与缆索所在抛物线关于y轴对称,
∴缆索 所在抛物线为
令 得 2,解得 或
又∵ ∴ FO 的长为40 m.
【例2】10 解析:根据题意,得抛物线经过点O(0,0),代入解析式 得 解得 ∴ 抛物线的解析式为 顶点坐标为(20,10),∴ 发射石块在空中飞行的最大高度为10 米.
2.1 8
2.2 解:(1)设运动员在空中运动时对应的抛物线的解析式为
∵ 抛物线经过原点, 解得
∴运动员在空中运动时对应的抛物线的解析式为
当 时, 解得 或 (舍去),
∴ 点 B 的坐标为
(2)当. 时, ∴调整点的坐标为
∴ 运动员此时距离水面高度为 (米).
∴运动员此次跳水不会失误.
将点 代入 得
当抛物线经过点 M时,
由①②联立方程组,解得
当抛物线经过点N时,
由①③联立方程组,解得
∵出水处点 D 在 MN 之间(包括M,N两点),
【例3】 450
【例4】 D 解析:由图象是经过原点的一条抛物线的一部分,设抛物线解析式为 把(1,165),(4,0)代入,得 解得 ∴ 抛物线解析式为 ∵ - 55 <0,∴当. 时,P取最大值220,∴变阻器 R 消耗的电功率P 最大为220 W.
【例5】 解:(1)设y与x之间的函数解析式为
将(100,300),(120,200)代入,得 解得
∴y与x之间的函数解析式为
(2)由题意,得 解得
设商场获得利润w元.根据题意,得
∴当 时,w取最大值,最大值为7920.
答:当销售单价为116时,商场获得利润最大,最大利润是7 920 元.
5.1 解:(1)设y与x的函数表达式为
由表中数据,得 解得
∴y与x的函数表达式为
(2)设日销售利润为w元.
由题意,得
∴当 时,w取得最大值,最大值为450.
答:糖果销售单价定为25 元时,所获日销售利润最大,最大利润是450元.
(3)由题意,得
∵最大利润为392元,
整理,得 解得
当 时,
∴每盒糖果的利润: (元),不合题意,舍去.
【例6】 解:(1)将点 D 的坐标代入抛物线 表达式,
得 解得 则抛物线 的表达式为
(2)由题意,得
当x=1时,
故点 D 在抛物线( 上.
(3)存在.
令 解得
当 为直角时,如图,过点 D作 且
则 为等腰直角三角形.
过点D 作 ∥轴,过点 B,E 分别作 GH的垂线,垂足分别为G,H.
∴E(2,2).
当 时,
∴点 E 在抛物线( 上,即点 P 为(2,2);
当 为直角时,如备用图,
同理可得△BGE≌△DHB(AAS),∴DH=3=BG,BH =1=GE,∴点 E(-1,3).
当x=-1时,
∴点 E 在抛物线( 上,即点为(-1,3);
当∠HPD 为直角时,如图3,
设点 E(x,y),同理可得△EHB≌△DGE(AAS),
∴ EH =x+2 =GD =y+1,BH =y =GE=1-x,解得x=0,y=1,即点 E(0,1).
当 时, 即点 E 不在抛物线上.
综上,在x轴上方的抛物线 上,存在点 P,使 是等腰直角三角形,点 P 的坐标为(2,2)或(
6.1 解:(1)将 代入
得 解得 ∴二次函数的表达式为 -2.
(2)设
的面积是 的面积的2倍,
解得 (舍去),
∴点 P 坐标为(
达标训练
1. D
2. C 解析:①令 则 解得 ∴小球从抛出到落
地需要6s ,故①正确;∴当时,h有最大值,最大值为45,∴小球运动中的高度可以是30 m,故②正确; 时,40(m),t=5 时, 25(m),∴小球运动2s时的高度大于运动5s时的高度,故③错误.
解析:如图,以O 为坐标原点,OM为 x轴正半轴,OP 为y轴正半轴,建立直角坐标系.
由题意可知, 顶点 B(5,4),则设抛物线顶点式为 将P(0,代入,得 解得 即抛物线的解析式为 令 解得 (不合题意,舍去),
4.能
5.解:设该果商定价为每吨x万元时每天的“利润”为w万元.
根据题意,得 312.5.
∴当 时,w有最大值,最大值为312.5.
答:该果商定价为每吨4.5万元时才能使每天的“利润”或“销售收入”最大,其最大值为312.5 万元.
6. B 解析:分别过点 A 和点 C 作 y轴的垂线,垂足分别为 M 和 N,如图.
由题意知,点 A 坐标为(m,点 C 坐标为 4)
CN
四边形 ABCD是正方形,∴AD=CD,∠ADC=90°,
∴ ∠CDN + ∠ADM = ∠ADM +∠DAM =90°,∴ ∠CDN = ∠DAM.
在△CDN 和 △DAM 中, ∴△CDN≌△DAM(AAS),
∴ DM = CN =n,DN=AM=m,∴MN=DM +DN=m+n.
又∵ 即(m+n)(m-n)=m+n.
∵m>n>0,∴m+n≠0,∴m-n=1.
7.46.4 解析:要使该矩形菜地面积最大,则要利用 OA 和 OC 构成矩形.设矩形在射线 OA 上的一段长为x m.
(1)当 x≤8 时,S =x·当x=8
时,S有最大值,
(2)当时, 47.61.
∵在的范围内,S均小于46.4.∴由(1)(2)得最大面积为
8.解:(1)由表可知,抛物线的顶点为(15,9),∴可设抛物线为
又∵抛物线过(10,8), 解得
∴抛物线的表达式为
(2)当 时,
∴水火箭距离地面的竖直高度为5m .
9.解:
②由①,得
∴火箭运行的最高点是
∴令
整理,得 解得 (不合题意,舍去),
由①,得 令
解得.
答:这两个位置之间的距离为8.4km.
(2)当 时, ∴火箭第二级的引发点的坐标为(9,
设火箭落地点与发射点的水平距离为15 km.
经过点 9),(15,0),
解得
∴当 时,火箭落地点与发射点的水平距离超过15 km.
10.解:(1)把点 代入 得 解得
∴ 抛物线的解析式为
(2)把 代入 得 解得 或
当 时, BC 的解析式为
根据题意,得D
轴, ∥轴,
即 BC·BD,
解得 或 (舍去).
(3)存在,点H 的坐标为 0)或 或 或 ,0).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 函数及其图象
第5节 二次函数的综合应用
考点分析
考点 1 抛物线型实际问题
课标要求导航:①通过对实际问题的分析,体会二次函数的意义;②能解决相应
的实际问题.
类型1 抛物线型建筑问题
例1 一条河上横跨着一座宏伟壮观的悬索桥.桥梁的缆索 与缆索 均呈抛物线型,桥塔AO 与桥塔BC 均垂直于桥面,如图所示,以O 为原点,以直线 为x轴,以桥塔AO 所在直线为y轴,建立平面直角坐标系.
已知:缆索 所在抛物线与缆索 所在抛物线关于y轴对称,桥塔AO与桥塔BC 之间的距离( 缆索 的最低点 P 到 的距离 .(桥塔的粗细忽略不计)
(1)求缆索. 所在抛物线的函数表达式;
(2)点E 在缆索 上, 且 求FO 的长.
例2 传统文化 如图1 所示的某种发石车是古代一种远程攻击的武器.将发石车置于山坡底部O处,以点O为原点,水平方向为x轴方向,建立如图2所示的平面直角坐标系,将发射出去的石块当作一个点看,其飞行路线可以近似看作抛物线 的一部分,则发射石块在空中飞行的最大高度为_________米.
2.1如图,这是巴黎奥运会足球比赛中某一时刻的鹰眼系统预测画面(图1)和截面示意图(图2),足球的飞行轨迹可看成抛物线,足球离地面的高度h(m)与足球被踢出后经过的时间t(s)之间的关系的部分数据如下表:
t/s 0 2 3 6 …
h/m 0 …
则该运动员踢出的足球在第________ s落地.
2.2综合与实践 学科实践
任务驱动:2024年世界泳联跳水世界杯第三站暨超级总决赛于4月19日至21日在中国陕西省西安市成功举办,中国国家跳水队以8金1银总奖牌9枚完美收官,进一步激发各地跳水运动员训练的热情.数学小组对跳水运动员跳水训练进行实践调查.
研究步骤:如图,某跳水运动员在10米跳台上进行跳水训练,水面与 y轴交于点E(0,-10),运动员(将运动员看成一点)在空中运动的路线是经过原点O 的抛物线,在跳某个规定动作时,运动员在空中最高处点A 的坐标为 正常情况下,运动员在距水面高度5米之前,必须完成规定的翻腾、打开动作,并调整好入水姿势,否则就会失误,运动员入水后,运动路线为另一条抛物线.
问题解决:请根据上述研究步骤与相关数据,完成下列任务.
(1)求运动员在空中运动时对应抛物线的解析式及入水处点 B 的坐标;
(2)若运动员在空中调整好入水姿势时,恰好与y轴的水平距离为3米,问该运动员此次跳水会不会失误 说明理由;
(3)在该运动员入水处点B 的正前方有M,N两点,且. 8,该运动员入水后运动路线对应的抛物线的解析式为 .若该运动员出水处点D在MN之间(包括M,N两点),请求出k的取值范围.
考点2 利用二次函数的性质解决最优问题
课标要求导航:①通过对实际问题的分析,体会二次函数的意义;②能解决相应的实际问题.
例3 如图,小明的父亲想用长为60米的栅栏,再借助房屋的外墙围成一个矩形的菜园.已知房屋外墙长40 米,则可围成的菜园的最大面积是__________平方米.
例3题图 例4题图
例4 跨物理学科 某物理兴趣小组对一款饮水机的工作电路展开研究,如图1,将变阻器R 的滑片从一端滑到另一端,绘制出变阻器R 消耗的电功率P 随电流I变化的关系图象,如图2所示,且该图象是经过原点的一条抛物线的一部分,则变阻器R 消耗的电功率P 最大为 ( )
A.160 W B.180 W C.200 W D.220 W
例5 某商场以每件80元的价格购进一种商品,在一段时间内,销售量y(单位:件)与销售单价x(单位:元/件)之间是一次函数关系,其部分图象如图所示.
(1)求这段时间内y与x之间的函数解析式;
(2)在这段时间内,若销售单价不低于100元,且商场还要完成不少于220件的销售任务,当销售单价为多少时,商场获得利润最大 最大利润是多少
5.1 某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(盒)与销售单价x(元)是一次函数关系,下表是y与x的几组对应值.
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 … 56 52 48 44 40 …
(1)求y与x的函数表达式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
考点3 与几何有关的二次函数综合题(
例6 如图,抛物线 的图象经过点 与x轴交于点A,点 B.
(1)求抛物线( 的表达式;
(2)将抛物线( 向右平移1个单位,再向上平移3个单位得到抛物线 求抛物线 的表达式,并判断点 D 是否在抛物线上;
(3)在x轴上方的抛物线( 上,是否存在点 P,使. 是等腰直角三角形.若存在,请求出点 P 的坐标;若不存在,请说明理由.
6.1 如图,已知二次函数 的图象与x轴交于A,B两点,与y轴交于点 C,其中
(1)求二次函数的表达式;
(2)若P 是二次函数图象上的一点,且点 P 在第二象限,线段 PC 交x轴于点D, 的面积是 的面积的2 倍,求点 P 的坐标.
达标训练
基础达标训练
1.一个球从地面竖直向上弹起时的速度为10米/秒,经过t(秒)时球距离地面的高度h(米)适用公式 那么球弹起后又回到地面所花的时间t(秒)是 ( )
A.5 B.10 C.1 D.2
2.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是 ≤t≤6).有下列结论:
①小球从抛出到落地需要6s;
②小球运动中的高度可以是30m;
③小球运动2 s时的高度小于运动5s 时的高度.
其中,正确结论的个数是 ( )
A.0 B.1 C.2 D.3
3.如图,壮壮同学投掷实心球,出手(点P 处)的高度OP 是 出手后实心球沿一段抛物线运行,到达最高点时,水平距离是5m ,高度是4m .若实心球落地点为M,则
4.真实问题情境 如图1为一汽车停车棚,其棚顶的横截面可以看作是抛物线的一部分,如图2 是棚顶的竖直高度y(单位:m)与距离停车棚支柱AO 的水平距离x(单位:m)近似满足函数关系 的图象,点B(6,2.68)在图象上.若一辆箱式货车需在停车棚下避雨,货车截面看作长高 的矩形,则可判定货车___________完全停到车棚内.(填“能”或“不能”)
5.广东省全力实施“百县千镇万村高质量发展工程”,2023 年农产品进出口总额居全国首位,其中荔枝鲜果远销欧美.某果商以每吨2万元的价格收购早熟荔枝,销往国外,若按每吨5万元出售,平均每天可售出100 吨.市场调查反映:如果每吨降价1万元,每天销售量相应增加50 吨.该果商如何定价才能使每天的“利润”或“销售收入”最大 并求出其最大值.(题中“元”为人民币)
高分提能训练
6.如图,正方形ABCD 的顶点A,C 在抛物线 上,点D 在y轴上.若A,C 两点的横坐标分别为下列结论正确的是 ( )
第6题图 第7题图
7.九(1)班劳动实践基地内有一块面积足够大的平整空地,地上两段围墙 于点O(如图),其中AB上的EO段围墙空缺.同学们测得 班长买来可切断的围栏 16 m,准备利用已有围墙,围出一块封闭的矩形菜地,则该菜地最大面积是__________
8.在校园科技节期间,科普员为同学们进行了水火箭的发射表演,图1是某型号水火箭的实物图,水火箭发射后的运动路线可以看作是一条抛物线.为了解水火箭的相关性能,同学们进一步展开研究.如图2 建立直角坐标系.水火箭发射后落在水平地面A处.科普员提供了该型号水火箭与地面成一定角度时,从发射到着陆过程中,水火箭距离地面OA 的竖直高度y(m)与离发射点 O 的水平距离x(m)的几组关系数据如下:
水平距离x(m) 0 3 4 10 15 20 22 27
竖直高度y(m) 0 3.24 4.16 8 9 8 7.04 3.24
(1)根据如表,请确定抛物线的表达式;
(2)请计算当水火箭飞行至离发射点O 的水平距离为5m 时,水火箭距离地面的竖直高度.
9.16世纪中叶,我国发明了一种新式火箭“火龙出水”,它是二级火箭的始祖.火箭第一级运行路径形如抛物线,当火箭运行一定水平距离时,自动引发火箭第二级,火箭第二级沿直线运行.
某科技小组运用信息技术模拟火箭运行过程.如图,以发射点为原点,地平线为x轴,垂直于地面的直线为 y 轴,建立平面直角坐标系,分别得到抛物线 和直线其中,当火箭运行的水平距离为9 km时,自动引发火箭的第二级.
(1)若火箭第二级的引发点的高度为3.6km,
①直接写出a,b的值;
②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低1.35 km,求这两个位置之间的距离.
(2)直接写出a满足什么条件时,火箭落地点与发射点的水平距离超过15 km.
冲刺满分训练
10.抛物线 与x轴交于 B两点,与y轴交于点C,点P 是第四象限内抛物线上的一点.
(1)求抛物线的解析式;
(2)如图1,过P作 轴于点D,交直线BC 于点 E.设点 D 的横坐标为m,当 时,求m 的值;
(3)如图2点 F(1,0),连接 CF 并延长交直线PD 于点 M,点N是x轴上方抛物线上的一点,在(2)的条件下,x轴上是否存在一点H,使得以F,M,N,H为顶点的四边形是平行四边形.若存在,直接写出点 H 的坐标;若不存在,请说明理由.
参考答案
【例1】解:(1)由题意,得A(0,17),抛物线的顶点 P 为(50,2).
故可设抛物线的函数表达式为
将A(0,17)代入,得 17,解得
∴缆索 所在抛物线的函数表达式为
(2)∵ 缆索. 所在抛物线与缆索所在抛物线关于y轴对称,
∴缆索 所在抛物线为
令 得 2,解得 或
又∵ ∴ FO 的长为40 m.
【例2】10 解析:根据题意,得抛物线经过点O(0,0),代入解析式 得 解得 ∴ 抛物线的解析式为 顶点坐标为(20,10),∴ 发射石块在空中飞行的最大高度为10 米.
2.1 8
2.2 解:(1)设运动员在空中运动时对应的抛物线的解析式为
∵ 抛物线经过原点, 解得
∴运动员在空中运动时对应的抛物线的解析式为
当 时, 解得 或 (舍去),
∴ 点 B 的坐标为
(2)当. 时, ∴调整点的坐标为
∴ 运动员此时距离水面高度为 (米).
∴运动员此次跳水不会失误.
将点 代入 得
当抛物线经过点 M时,
由①②联立方程组,解得
当抛物线经过点N时,
由①③联立方程组,解得
∵出水处点 D 在 MN 之间(包括M,N两点),
【例3】 450
【例4】 D 解析:由图象是经过原点的一条抛物线的一部分,设抛物线解析式为 把(1,165),(4,0)代入,得 解得 ∴ 抛物线解析式为 ∵ - 55 <0,∴当. 时,P取最大值220,∴变阻器 R 消耗的电功率P 最大为220 W.
【例5】 解:(1)设y与x之间的函数解析式为
将(100,300),(120,200)代入,得 解得
∴y与x之间的函数解析式为
(2)由题意,得 解得
设商场获得利润w元.根据题意,得
∴当 时,w取最大值,最大值为7920.
答:当销售单价为116时,商场获得利润最大,最大利润是7 920 元.
5.1 解:(1)设y与x的函数表达式为
由表中数据,得 解得
∴y与x的函数表达式为
(2)设日销售利润为w元.
由题意,得
∴当 时,w取得最大值,最大值为450.
答:糖果销售单价定为25 元时,所获日销售利润最大,最大利润是450元.
(3)由题意,得
∵最大利润为392元,
整理,得 解得
当 时,
∴每盒糖果的利润: (元),不合题意,舍去.
【例6】 解:(1)将点 D 的坐标代入抛物线 表达式,
得 解得 则抛物线 的表达式为
(2)由题意,得
当x=1时,
故点 D 在抛物线( 上.
(3)存在.
令 解得
当 为直角时,如图,过点 D作 且
则 为等腰直角三角形.
过点D 作 ∥轴,过点 B,E 分别作 GH的垂线,垂足分别为G,H.
∴E(2,2).
当 时,
∴点 E 在抛物线( 上,即点 P 为(2,2);
当 为直角时,如备用图,
同理可得△BGE≌△DHB(AAS),∴DH=3=BG,BH =1=GE,∴点 E(-1,3).
当x=-1时,
∴点 E 在抛物线( 上,即点为(-1,3);
当∠HPD 为直角时,如图3,
设点 E(x,y),同理可得△EHB≌△DGE(AAS),
∴ EH =x+2 =GD =y+1,BH =y =GE=1-x,解得x=0,y=1,即点 E(0,1).
当 时, 即点 E 不在抛物线上.
综上,在x轴上方的抛物线 上,存在点 P,使 是等腰直角三角形,点 P 的坐标为(2,2)或(
6.1 解:(1)将 代入
得 解得 ∴二次函数的表达式为 -2.
(2)设
的面积是 的面积的2倍,
解得 (舍去),
∴点 P 坐标为(
达标训练
1. D
2. C 解析:①令 则 解得 ∴小球从抛出到落
地需要6s ,故①正确;∴当时,h有最大值,最大值为45,∴小球运动中的高度可以是30 m,故②正确; 时,40(m),t=5 时, 25(m),∴小球运动2s时的高度大于运动5s时的高度,故③错误.
解析:如图,以O 为坐标原点,OM为 x轴正半轴,OP 为y轴正半轴,建立直角坐标系.
由题意可知, 顶点 B(5,4),则设抛物线顶点式为 将P(0,代入,得 解得 即抛物线的解析式为 令 解得 (不合题意,舍去),
4.能
5.解:设该果商定价为每吨x万元时每天的“利润”为w万元.
根据题意,得 312.5.
∴当 时,w有最大值,最大值为312.5.
答:该果商定价为每吨4.5万元时才能使每天的“利润”或“销售收入”最大,其最大值为312.5 万元.
6. B 解析:分别过点 A 和点 C 作 y轴的垂线,垂足分别为 M 和 N,如图.
由题意知,点 A 坐标为(m,点 C 坐标为 4)
CN
四边形 ABCD是正方形,∴AD=CD,∠ADC=90°,
∴ ∠CDN + ∠ADM = ∠ADM +∠DAM =90°,∴ ∠CDN = ∠DAM.
在△CDN 和 △DAM 中, ∴△CDN≌△DAM(AAS),
∴ DM = CN =n,DN=AM=m,∴MN=DM +DN=m+n.
又∵ 即(m+n)(m-n)=m+n.
∵m>n>0,∴m+n≠0,∴m-n=1.
7.46.4 解析:要使该矩形菜地面积最大,则要利用 OA 和 OC 构成矩形.设矩形在射线 OA 上的一段长为x m.
(1)当 x≤8 时,S =x·当x=8
时,S有最大值,
(2)当时, 47.61.
∵在的范围内,S均小于46.4.∴由(1)(2)得最大面积为
8.解:(1)由表可知,抛物线的顶点为(15,9),∴可设抛物线为
又∵抛物线过(10,8), 解得
∴抛物线的表达式为
(2)当 时,
∴水火箭距离地面的竖直高度为5m .
9.解:
②由①,得
∴火箭运行的最高点是
∴令
整理,得 解得 (不合题意,舍去),
由①,得 令
解得.
答:这两个位置之间的距离为8.4km.
(2)当 时, ∴火箭第二级的引发点的坐标为(9,
设火箭落地点与发射点的水平距离为15 km.
经过点 9),(15,0),
解得
∴当 时,火箭落地点与发射点的水平距离超过15 km.
10.解:(1)把点 代入 得 解得
∴ 抛物线的解析式为
(2)把 代入 得 解得 或
当 时, BC 的解析式为
根据题意,得D
轴, ∥轴,
即 BC·BD,
解得 或 (舍去).
(3)存在,点H 的坐标为 0)或 或 或 ,0).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
