2024-2025学年上海市静安区风华中学高二(上)期末数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年上海市静安区风华中学高二(上)期末数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 104.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 15:20:30 | ||
图片预览



文档简介
2024-2025学年上海市静安区风华中学高二(上)期末数学试卷
一、单选题:本题共3小题,每小题5分,共15分。在每小题给出的选项中,只有一项是符合题目要求的。
1.空间两条互相平行的直线指的是( )
A. 在空间没有公共点的两条直线
B. 分别在两个平面上的两条直线
C. 在两个不同的平面上且没有公共点的两条直线
D. 在同一平面上且没有公共点的两条直线
2.方程的解集是( )
A. B. C. D.
3.祖暅,又名祖暅之,是我国南北朝时期的数学家、天文学家祖冲之的儿子他在级术中提出“幂势既同,则积不容异”的结论,其中“幂”是面积“势”是高,意思就是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任一平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等如图这一原理主要应用于计算一些复杂几何体的体积,若某艺术品如图所示,高为,底面为边长的正三角形挖去以底边为直径的圆如图,则该艺术品的体积为( )
A. B.
C. D.
二、填空题:本题共10小题,每小题5分,共50分。
4.空间中已知直线,直线,直线,若直线直线,直线与直线异面,则直线与直线的位置关系是______.
5.在的二项展开式中,的系数是______用数字作答.
6.甲、乙同时炮击一架敌机,已知甲击中敌机的概率为,乙击中敌机的概率为,敌机被击中的概率为______.
7.球的表面积扩大为原来的倍,它的体积扩大为原来的______ 倍.
8.甲、乙等五名社区志愿者被随机分配到、、、四个不同岗位服务,每个岗位至少有一名志愿者,则甲、乙两人同时参加岗位服务的排法有______种
9.以下数据为参加数学竞赛决赛的人的成绩单位:分,分数从低到高依次:,,,,,,,,,,,,,,,则这人成绩的第百分位数是 .
10.有以下命题:
若,则与、共面;
若与、共面,则;
若,则、、、共面;
若、、、共面,则则所有真命题的序号为______.
11.如图是某班一次数学测试成绩的茎叶图图中仅列出,的数据和频率分布直方图,则 ______.
12.如图,在棱长为的正方体中,为线段上的动点不含端点,则下列结论正确的是______.
平面平面;
;
的取值范围是;
三棱锥的体积为定值.
13.已知四棱柱底面为平行四边形,,且,则异面直线与的夹角余弦值为______.
三、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
14.本小题分
如图,在四面体中,,,、分别为、的中点,并且异面直线与所成的角为求的长.
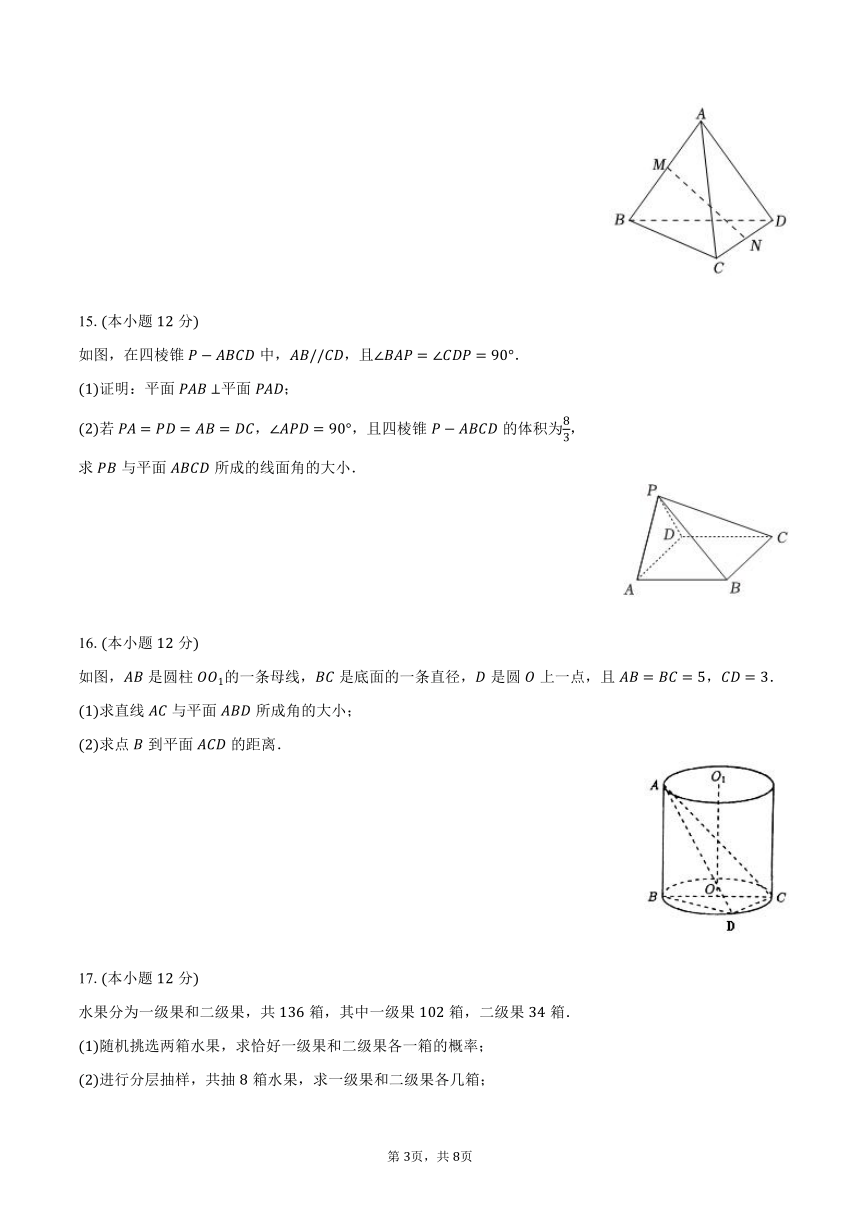
15.本小题分
如图,在四棱锥中,,且.
证明:平面平面;
若,,且四棱锥的体积为,
求与平面所成的线面角的大小.
16.本小题分
如图,是圆柱的一条母线,是底面的一条直径,是圆上一点,且,.
求直线与平面所成角的大小;
求点到平面的距离.
17.本小题分
水果分为一级果和二级果,共箱,其中一级果箱,二级果箱.
随机挑选两箱水果,求恰好一级果和二级果各一箱的概率;
进行分层抽样,共抽箱水果,求一级果和二级果各几箱;
抽取若干箱水果,其中一级果共个,单果质量平均数为克,方差为;二级果个,单果质量平均数为克,方差为;求个水果的方差和平均数,并预估果园中单果的质量.
18.本小题分
在四棱锥中,底面是矩形,平面,,,以的中点为球心、为直径的球面交于点,交于点.
求证:平面;
求直线与平面所成角的正弦值;
求点到平面的距离.
参考答案
1.
2.
3.
4.相交或异面
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.解:取中点,连接,,
又因为,,,分别为,的中点,
所以,,,,
又因为异面直线与所成的角为,所以,
所以,
所以.
15.证明:在四棱锥中,,
,,
又,
,
,
平面,
平面,
平面平面;
解:取中点,连结,
,为的中点,
,
平面,平面,
,
,
底面,
设,
则,,
四棱锥的体积为,底面,
,解得,
,
,
底面,
为与平面所成的角,
在中,,
,
故与平面所成的线面角为.
16.解:平面,平面,
,
是圆的直径,
,
又平面,平面,,
平面.
是与平面所成的角.
,,
.
直线与平面所成角的大小为.
过作,垂足为,
由得平面,平面,
平面平面,
又平面平面,平面,,
平面.
,.
.
即到平面的距离为.
17.解:古典概型:设事件为恰好选到一级果和二级果各一箱,样本空间的样本点的个数,
事件的样本点的公式,
所以;
因为一级果箱数:二级果箱数:,
所以箱水果中有一级果抽取箱,二级果抽取箱;
设一级果平均质量为,方差为,二级果质量为,方差为,总体样本平均质量为平均值,方差为,
因为,,,,
所以克,
克.
预估:平均质量为克.
18.解:证明:依题设知,是所作球面的直径,则,
平面,
则,
又,,平面,,
平面,
又平面,
则,
又,,平面,
平面;
由知,,
又,则是的中点,
则,,
则,
设到平面的距离为,
由得,
可求得,
设直线与平面所成角的大小为,
则;
由已知求得,
易知,
由得,
,
故点到平面的距离等于点到平面距离的,
又是的中点,则、到平面的距离相等,
由可知所求距离为.
第1页,共1页
一、单选题:本题共3小题,每小题5分,共15分。在每小题给出的选项中,只有一项是符合题目要求的。
1.空间两条互相平行的直线指的是( )
A. 在空间没有公共点的两条直线
B. 分别在两个平面上的两条直线
C. 在两个不同的平面上且没有公共点的两条直线
D. 在同一平面上且没有公共点的两条直线
2.方程的解集是( )
A. B. C. D.
3.祖暅,又名祖暅之,是我国南北朝时期的数学家、天文学家祖冲之的儿子他在级术中提出“幂势既同,则积不容异”的结论,其中“幂”是面积“势”是高,意思就是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任一平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等如图这一原理主要应用于计算一些复杂几何体的体积,若某艺术品如图所示,高为,底面为边长的正三角形挖去以底边为直径的圆如图,则该艺术品的体积为( )
A. B.
C. D.
二、填空题:本题共10小题,每小题5分,共50分。
4.空间中已知直线,直线,直线,若直线直线,直线与直线异面,则直线与直线的位置关系是______.
5.在的二项展开式中,的系数是______用数字作答.
6.甲、乙同时炮击一架敌机,已知甲击中敌机的概率为,乙击中敌机的概率为,敌机被击中的概率为______.
7.球的表面积扩大为原来的倍,它的体积扩大为原来的______ 倍.
8.甲、乙等五名社区志愿者被随机分配到、、、四个不同岗位服务,每个岗位至少有一名志愿者,则甲、乙两人同时参加岗位服务的排法有______种
9.以下数据为参加数学竞赛决赛的人的成绩单位:分,分数从低到高依次:,,,,,,,,,,,,,,,则这人成绩的第百分位数是 .
10.有以下命题:
若,则与、共面;
若与、共面,则;
若,则、、、共面;
若、、、共面,则则所有真命题的序号为______.
11.如图是某班一次数学测试成绩的茎叶图图中仅列出,的数据和频率分布直方图,则 ______.
12.如图,在棱长为的正方体中,为线段上的动点不含端点,则下列结论正确的是______.
平面平面;
;
的取值范围是;
三棱锥的体积为定值.
13.已知四棱柱底面为平行四边形,,且,则异面直线与的夹角余弦值为______.
三、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
14.本小题分
如图,在四面体中,,,、分别为、的中点,并且异面直线与所成的角为求的长.
15.本小题分
如图,在四棱锥中,,且.
证明:平面平面;
若,,且四棱锥的体积为,
求与平面所成的线面角的大小.
16.本小题分
如图,是圆柱的一条母线,是底面的一条直径,是圆上一点,且,.
求直线与平面所成角的大小;
求点到平面的距离.
17.本小题分
水果分为一级果和二级果,共箱,其中一级果箱,二级果箱.
随机挑选两箱水果,求恰好一级果和二级果各一箱的概率;
进行分层抽样,共抽箱水果,求一级果和二级果各几箱;
抽取若干箱水果,其中一级果共个,单果质量平均数为克,方差为;二级果个,单果质量平均数为克,方差为;求个水果的方差和平均数,并预估果园中单果的质量.
18.本小题分
在四棱锥中,底面是矩形,平面,,,以的中点为球心、为直径的球面交于点,交于点.
求证:平面;
求直线与平面所成角的正弦值;
求点到平面的距离.
参考答案
1.
2.
3.
4.相交或异面
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.解:取中点,连接,,
又因为,,,分别为,的中点,
所以,,,,
又因为异面直线与所成的角为,所以,
所以,
所以.
15.证明:在四棱锥中,,
,,
又,
,
,
平面,
平面,
平面平面;
解:取中点,连结,
,为的中点,
,
平面,平面,
,
,
底面,
设,
则,,
四棱锥的体积为,底面,
,解得,
,
,
底面,
为与平面所成的角,
在中,,
,
故与平面所成的线面角为.
16.解:平面,平面,
,
是圆的直径,
,
又平面,平面,,
平面.
是与平面所成的角.
,,
.
直线与平面所成角的大小为.
过作,垂足为,
由得平面,平面,
平面平面,
又平面平面,平面,,
平面.
,.
.
即到平面的距离为.
17.解:古典概型:设事件为恰好选到一级果和二级果各一箱,样本空间的样本点的个数,
事件的样本点的公式,
所以;
因为一级果箱数:二级果箱数:,
所以箱水果中有一级果抽取箱,二级果抽取箱;
设一级果平均质量为,方差为,二级果质量为,方差为,总体样本平均质量为平均值,方差为,
因为,,,,
所以克,
克.
预估:平均质量为克.
18.解:证明:依题设知,是所作球面的直径,则,
平面,
则,
又,,平面,,
平面,
又平面,
则,
又,,平面,
平面;
由知,,
又,则是的中点,
则,,
则,
设到平面的距离为,
由得,
可求得,
设直线与平面所成角的大小为,
则;
由已知求得,
易知,
由得,
,
故点到平面的距离等于点到平面距离的,
又是的中点,则、到平面的距离相等,
由可知所求距离为.
第1页,共1页
同课章节目录
