专题四:综合训练题 寒假提高练(一) 2024--2025学年初中数学人教版八年级上册
文档属性
| 名称 | 专题四:综合训练题 寒假提高练(一) 2024--2025学年初中数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 587.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 16:59:33 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题四:综合训练题 寒假提高练(一)
2024--2025学年初中数学人教版八年级上册
一、单选题
1.分式方程的根是( )
A. B. C. D.
2.点关于y轴的对称点的坐标是( )
A. B. C. D.
3.下列计算正确的是( )
A. B.
C. D.
4.如图,已知,则的值( )
A.不确定 B.等于1 C.等于2 D.大于2
5.若分式有意义,则x的取值范围是( )
A.x≠0 B. C. D.
6.如图,在△ABC中,∠BAC>90°,D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连接AD、CF,则图中所有的等腰三角形的个数为( )
A.1 B.2 C.3 D.4
7.具备下列条件的两个三角形,可以证明它们全等的是( ).
A.一边和这一边上的高对应相等 B.两边和第三边上的中线对应相等
C.两边和其中一边的对角对应相等 D.直角三角形的斜边对应相等
8.如图,在中,,是的角平分线,于点E,给出四个结论:①,②,③,④,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
9.如图,已知,,下列条件中,无法判断△ABC≌△DEC的是( )
A. B. C. D.
10.如图,在中,和的平分线、相交于点,过点作于点.则下列结论中错误的是( )
A.
B.
C.若,,则
D.当时,
二、填空题
11.当 时,分式的值为零.
12.如图,已知,当添加条件 时,可由“角边角”判定.
13.已知,则 .
14.甲、乙两人站在一条道路的两端同时出发相向而行,1.2小时相遇,若甲走完这条道路需2小时,则乙走完这条路需 小时.
15.若一个多边形的每个外角都等于,则这个多边形的边数为 .
16.已知关于x的分式方程有一个正数解,则k的取值范围为 .
三、解答题
17.计算
18.解分式方程:.
19.如图,在四边形中,,点为中点,且平分,.
(1)求证:平分;
(2)求证:.
20.如图,在△ABC中,∠ACB=90°,∠A=30°,D为AB上一点,以CD为边在CD右侧作等边△CDE.
(1)如图1,当点E在边AC上时,求证:DE=AE;
(2)如图2,当点E在△ABC内部时,猜想ED和EA数量关系;
(3)当点E在△ABC外部时,过点E作EH⊥AB点H,EF∥AB,CF=2,AH=3.直接写出AB的长为 .
21.如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.
(1)求C点的坐标;
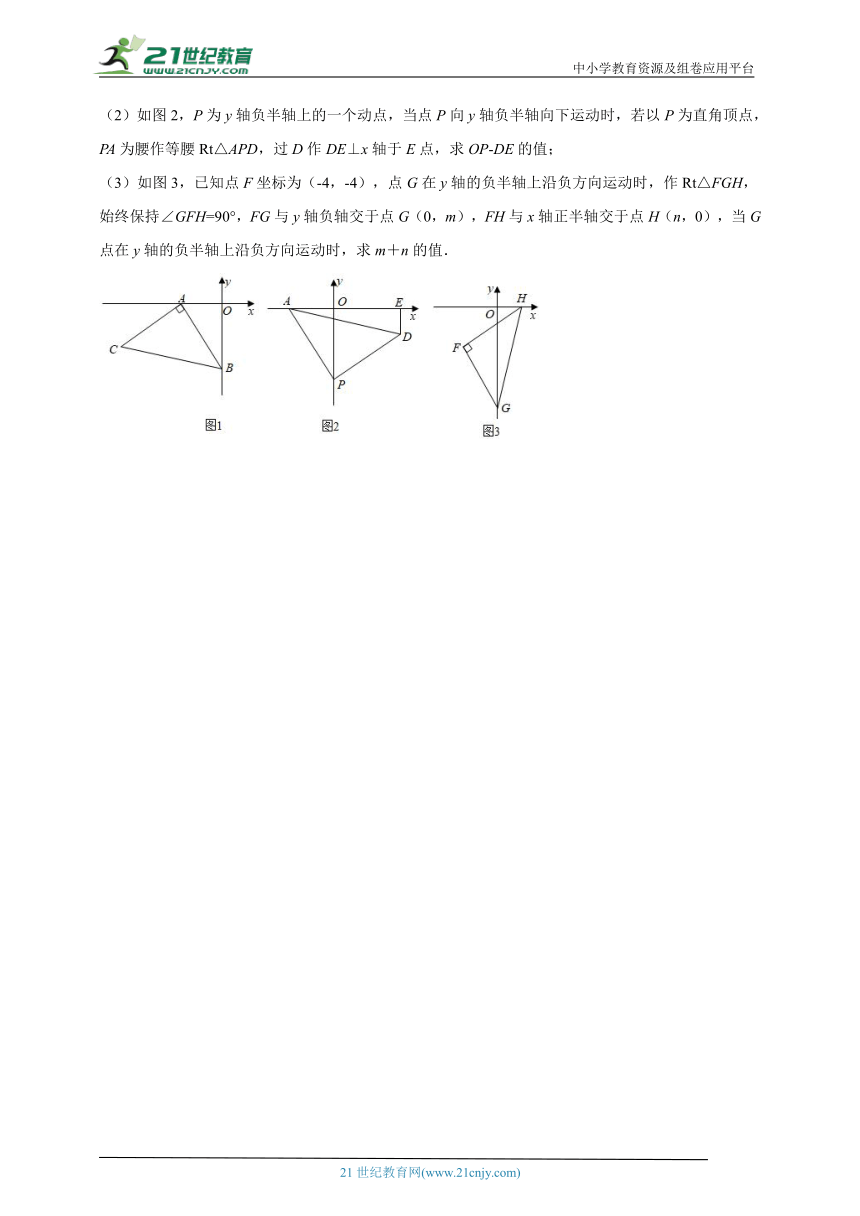
(2)如图2,P为y轴负半轴上的一个动点,当点P向y轴负半轴向下运动时,若以P为直角顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OP-DE的值;
(3)如图3,已知点F坐标为(-4,-4),点G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90°,FG与y轴负轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,求m+n的值.
参考答案:
1.D
解:原式=3x-1-2-3=0,3x=6,x=2,
经检验x=2是方程的解,
2.A
解:由点关于y轴对称的点的坐标是,
3.D
解:A. ,故该选项不正确,不符合题意;
B. ,故该选项不正确,不符合题意;
C. ,故该选项不正确,不符合题意;
D. ,故该选项正确,符合题意;
4.C
解:根据三角形的外角性质可得:∠AFE=∠ABF+∠BAF,∠AEC=∠BAE+∠ABF,
∵AF∥CD,
∴∠AFE=∠ECD,
∴∠ECD=∠ABF+∠BAF,
∵∠BAF=∠EAF,
∴∠BAE=2∠BAF,
∴∠AEC+∠ABF=∠BAE+∠ABF+∠ABF=2∠BAF+2∠ABF=2(∠BAF+∠ABF),
∴,
5.B
解:由题意,得
1-2x≠0,
解得:x≠,
6.D
解:如图:∵D为BC的中点,
∴BD=CD,
∵将△CDE沿DE折叠,
∴CD=DF,EF=EC,
∴BD=CD=DF,
∴△BDF,△CDF,△EFC是等腰三角形,
∴EF=EC,
∴∠EFC=∠ECF,
∴∠FAE=∠AFE,
∴EF=AE,
∴△AEF是等腰三角形,
∴图中所有的等腰三角形的个数为4.
7.B
解:A、一边和这边上的高对应相等,无法得出它们全等,故此选项错误;
B、两边和第三边上的中线对应相等,通过如图所示方式(倍长中线法)可以证明它们全等(△ABC≌△A′B′C′),故此选项正确.
C、两边和其中一边的对角对应相等,无法利用ASS得出它们全等,故此选项错误;
D、直角三角形的斜边对应相等,无法得出它们全等,故此选项错误.
8.B
解:∵是的角平分线,
∴,
∵于点E,
∴,
∵,
∴,
∴,
故①②③符合题意;
∵,
∴,
∵,
∴,
故④不符合题意.
∴其中正确的有3个.
9.D
解:添加条件,结合条件,,可以根据证明,故A不符合题意;
添加条件,结合条件,,可以根据证明,故B不符合题意;
∵添加条件,
∴,即,结合条件,,可以根据证明,故A不符合题意;
添加条件,结合条件,,不可以根据证明,故D符合题意;
10.C
解:∵和的平分线,相交于点O,
∴,,
∴
,故A正确,不符合题意;
设中边上的高为h,
∵,即;故B正确,不符合题意;
如图所示,作于H,于M,
∵和的平分线相交于点O,
∴点O在的平分线上,
∴,
∵,
∴
,故C错误,符合题意;
∵,
∴,
∵,分别是和的平分线,
∴,
∴,
∴,
∴,
如图所示,在上取一点H,使,
∵是的角平分线,
∴,
在和中,
,
∴,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴,故D正确,不符合题意;
11.
解:∵分式的值为零,
∴且,
解得,
故答案为:.
12./
解:依题意可知,应添加,
∵在和中,
,
∴(),
故答案为:.
13.
解:∵,
∵,
∴,
故答案为:.
14.3
设乙走完这条路需x小时,则甲的速度为,乙的速度为,根据题意得,
,
解得,x=3,
经检验,x=3是原方程的解,
所以,乙走完这条路需3小时.
故答案为3.
15.12
解:由题意,这个多边形的边数为;
故答案为:12.
16.k<6且k≠3
解:,
方程两边都乘以(x-3),得
x=2(x-3)+k,
解得x=6-k≠3,
关于x的方程程有一个正数解,
∴x=6-k>0,
k<6,且k≠3,
∴k的取值范围是k<6且k≠3.
故答案为k<6且k≠3.
17.
解:原式.
.
18.
解:在方程两边同时乘以,得:
,
解得:,
检验:当时,,
∴是分式方程的解.
19.(1)见解析
(2)见解析
(1)如图,延长交延长线于点E,
∵O为中点,
∴,
在和中,
∴,
∴,
∵,
∴,
∴平分;
(2)∵,
∴,
∵,
∴.
20.(1)见解析;(2)ED=EA,理由见解析;(3)16
(1)证明:∵△CDE是等边三角形,
∴∠CED=∠DCE=60°,
∴∠EDA=60°﹣∠A=30°,
∵∠A=30°,
∴∠EDA=30°,
∴∠EDA=∠B,
∴DE=EA;
(2)结论:ED=EA,理由:
如图2中,取AB的中点O、EO,
∵∠ACB=90°,∠BAC=30°,
∴∠B=60°,OC=OB,
∴△BCO为等边三角形,
∴CB=CO=BO=AO,
∵△CDE是等边三角形,
∴∠BCD=∠OCE,
在△BCD和△OCE中,
,
∴△BCD≌△OCE(SAS),
∴∠COE=∠B=60°,
∴∠AOE=60°,
在△COE和△AOE中,
,
∴△COE≌△AOE(SAS),
∴EC=EA,
∴ED=EA;
(3)解:如图3中,取AB的中点O、连接EO,AE,
由(2)得△BCD≌△OCE,
∴∠COE=∠B=60°,
∴∠AOE=60°,
同法可得△COE≌△AOE,
∴EC=EA,
∴ED=EA,
∵EH⊥AB,
∴DH=AH=5,
∵EF∥AB,
∴∠F=180°﹣∠B=120°,
∵∠FCD=∠FCE+60°=∠CDB+60°,
∴∠FCE=∠CDB,
在△CEF和△DCO中,
,
∴△CEF≌△DCO(AAS),
∴CF=OD=2,
∴OA=OD+AD=2+6=8,
∴AB=2OA=16.
21.(1)(-6,-2);(2)2;(3)-8
解:(1)过点C作CM⊥x轴于点M,
∵CM⊥OA,AC⊥AB,∠BOA=90°,
∴∠CMA=∠CAB=∠AOB=90°
∴∠MAC+∠OAB=90°,∠OAB +∠OBA=90°,
∴∠MAC=∠OBA,
∵△ABC是以AB为腰的等腰直角三角形,
∴AC=AB,
在△MAC和△OBA中,
,
∴△MAC≌△OBA(AAS),
∴CM=OA=2 ,MA=OB=4,
∴OM=OA+MA=6
∴点C的坐标为(-6,-2);
(2)过点D作DQ⊥OP于Q,
∵DQ⊥OP,DE⊥OE,∠POE=90°,
∴OE=QD,DE=OQ,
∴OP=PQ+OQ=DE+PQ,
∴∠APO+∠QPD=∠APD=90° ∠APO+∠OAP=90°,
∴∠QPD =∠OAP,
∵△APD是以P为直角顶点,AP为腰的等腰直角三角形,
∴AP=PD
在△AOP和△PDQ中,
,
∴△AOP≌△PDQ(AAS),
∴QP=AO=2,
∴OP-DE=PQ=2;
(3)过点F作FS⊥x轴于S,FT⊥y轴于T,
∵F(-4,-4),
∴FS=FT=4,
∵FT⊥y轴,SH⊥y轴
∴∠FHS=∠HFT,
∵∠FGT+∠GFT=∠HFT+∠GFT=90°,
∴∠FHS=∠HFT=∠FGT,
在△FSH和△FTG中,
,
∴△FSH≌△FTG(AAS)
∴GT=HS,
又∵G(0,m),H(n,0),点F坐标为(-4,-4)
∴OT=OS=4,OG=-m,OH=n,
∴GT=OG-OT=-m-4, HS=OH+OS=n+4,
∴-m-4= n+4,
∴m+n=-8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题四:综合训练题 寒假提高练(一)
2024--2025学年初中数学人教版八年级上册
一、单选题
1.分式方程的根是( )
A. B. C. D.
2.点关于y轴的对称点的坐标是( )
A. B. C. D.
3.下列计算正确的是( )
A. B.
C. D.
4.如图,已知,则的值( )
A.不确定 B.等于1 C.等于2 D.大于2
5.若分式有意义,则x的取值范围是( )
A.x≠0 B. C. D.
6.如图,在△ABC中,∠BAC>90°,D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连接AD、CF,则图中所有的等腰三角形的个数为( )
A.1 B.2 C.3 D.4
7.具备下列条件的两个三角形,可以证明它们全等的是( ).
A.一边和这一边上的高对应相等 B.两边和第三边上的中线对应相等
C.两边和其中一边的对角对应相等 D.直角三角形的斜边对应相等
8.如图,在中,,是的角平分线,于点E,给出四个结论:①,②,③,④,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
9.如图,已知,,下列条件中,无法判断△ABC≌△DEC的是( )
A. B. C. D.
10.如图,在中,和的平分线、相交于点,过点作于点.则下列结论中错误的是( )
A.
B.
C.若,,则
D.当时,
二、填空题
11.当 时,分式的值为零.
12.如图,已知,当添加条件 时,可由“角边角”判定.
13.已知,则 .
14.甲、乙两人站在一条道路的两端同时出发相向而行,1.2小时相遇,若甲走完这条道路需2小时,则乙走完这条路需 小时.
15.若一个多边形的每个外角都等于,则这个多边形的边数为 .
16.已知关于x的分式方程有一个正数解,则k的取值范围为 .
三、解答题
17.计算
18.解分式方程:.
19.如图,在四边形中,,点为中点,且平分,.
(1)求证:平分;
(2)求证:.
20.如图,在△ABC中,∠ACB=90°,∠A=30°,D为AB上一点,以CD为边在CD右侧作等边△CDE.
(1)如图1,当点E在边AC上时,求证:DE=AE;
(2)如图2,当点E在△ABC内部时,猜想ED和EA数量关系;
(3)当点E在△ABC外部时,过点E作EH⊥AB点H,EF∥AB,CF=2,AH=3.直接写出AB的长为 .
21.如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.
(1)求C点的坐标;
(2)如图2,P为y轴负半轴上的一个动点,当点P向y轴负半轴向下运动时,若以P为直角顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OP-DE的值;
(3)如图3,已知点F坐标为(-4,-4),点G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90°,FG与y轴负轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,求m+n的值.
参考答案:
1.D
解:原式=3x-1-2-3=0,3x=6,x=2,
经检验x=2是方程的解,
2.A
解:由点关于y轴对称的点的坐标是,
3.D
解:A. ,故该选项不正确,不符合题意;
B. ,故该选项不正确,不符合题意;
C. ,故该选项不正确,不符合题意;
D. ,故该选项正确,符合题意;
4.C
解:根据三角形的外角性质可得:∠AFE=∠ABF+∠BAF,∠AEC=∠BAE+∠ABF,
∵AF∥CD,
∴∠AFE=∠ECD,
∴∠ECD=∠ABF+∠BAF,
∵∠BAF=∠EAF,
∴∠BAE=2∠BAF,
∴∠AEC+∠ABF=∠BAE+∠ABF+∠ABF=2∠BAF+2∠ABF=2(∠BAF+∠ABF),
∴,
5.B
解:由题意,得
1-2x≠0,
解得:x≠,
6.D
解:如图:∵D为BC的中点,
∴BD=CD,
∵将△CDE沿DE折叠,
∴CD=DF,EF=EC,
∴BD=CD=DF,
∴△BDF,△CDF,△EFC是等腰三角形,
∴EF=EC,
∴∠EFC=∠ECF,
∴∠FAE=∠AFE,
∴EF=AE,
∴△AEF是等腰三角形,
∴图中所有的等腰三角形的个数为4.
7.B
解:A、一边和这边上的高对应相等,无法得出它们全等,故此选项错误;
B、两边和第三边上的中线对应相等,通过如图所示方式(倍长中线法)可以证明它们全等(△ABC≌△A′B′C′),故此选项正确.
C、两边和其中一边的对角对应相等,无法利用ASS得出它们全等,故此选项错误;
D、直角三角形的斜边对应相等,无法得出它们全等,故此选项错误.
8.B
解:∵是的角平分线,
∴,
∵于点E,
∴,
∵,
∴,
∴,
故①②③符合题意;
∵,
∴,
∵,
∴,
故④不符合题意.
∴其中正确的有3个.
9.D
解:添加条件,结合条件,,可以根据证明,故A不符合题意;
添加条件,结合条件,,可以根据证明,故B不符合题意;
∵添加条件,
∴,即,结合条件,,可以根据证明,故A不符合题意;
添加条件,结合条件,,不可以根据证明,故D符合题意;
10.C
解:∵和的平分线,相交于点O,
∴,,
∴
,故A正确,不符合题意;
设中边上的高为h,
∵,即;故B正确,不符合题意;
如图所示,作于H,于M,
∵和的平分线相交于点O,
∴点O在的平分线上,
∴,
∵,
∴
,故C错误,符合题意;
∵,
∴,
∵,分别是和的平分线,
∴,
∴,
∴,
∴,
如图所示,在上取一点H,使,
∵是的角平分线,
∴,
在和中,
,
∴,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴,故D正确,不符合题意;
11.
解:∵分式的值为零,
∴且,
解得,
故答案为:.
12./
解:依题意可知,应添加,
∵在和中,
,
∴(),
故答案为:.
13.
解:∵,
∵,
∴,
故答案为:.
14.3
设乙走完这条路需x小时,则甲的速度为,乙的速度为,根据题意得,
,
解得,x=3,
经检验,x=3是原方程的解,
所以,乙走完这条路需3小时.
故答案为3.
15.12
解:由题意,这个多边形的边数为;
故答案为:12.
16.k<6且k≠3
解:,
方程两边都乘以(x-3),得
x=2(x-3)+k,
解得x=6-k≠3,
关于x的方程程有一个正数解,
∴x=6-k>0,
k<6,且k≠3,
∴k的取值范围是k<6且k≠3.
故答案为k<6且k≠3.
17.
解:原式.
.
18.
解:在方程两边同时乘以,得:
,
解得:,
检验:当时,,
∴是分式方程的解.
19.(1)见解析
(2)见解析
(1)如图,延长交延长线于点E,
∵O为中点,
∴,
在和中,
∴,
∴,
∵,
∴,
∴平分;
(2)∵,
∴,
∵,
∴.
20.(1)见解析;(2)ED=EA,理由见解析;(3)16
(1)证明:∵△CDE是等边三角形,
∴∠CED=∠DCE=60°,
∴∠EDA=60°﹣∠A=30°,
∵∠A=30°,
∴∠EDA=30°,
∴∠EDA=∠B,
∴DE=EA;
(2)结论:ED=EA,理由:
如图2中,取AB的中点O、EO,
∵∠ACB=90°,∠BAC=30°,
∴∠B=60°,OC=OB,
∴△BCO为等边三角形,
∴CB=CO=BO=AO,
∵△CDE是等边三角形,
∴∠BCD=∠OCE,
在△BCD和△OCE中,
,
∴△BCD≌△OCE(SAS),
∴∠COE=∠B=60°,
∴∠AOE=60°,
在△COE和△AOE中,
,
∴△COE≌△AOE(SAS),
∴EC=EA,
∴ED=EA;
(3)解:如图3中,取AB的中点O、连接EO,AE,
由(2)得△BCD≌△OCE,
∴∠COE=∠B=60°,
∴∠AOE=60°,
同法可得△COE≌△AOE,
∴EC=EA,
∴ED=EA,
∵EH⊥AB,
∴DH=AH=5,
∵EF∥AB,
∴∠F=180°﹣∠B=120°,
∵∠FCD=∠FCE+60°=∠CDB+60°,
∴∠FCE=∠CDB,
在△CEF和△DCO中,
,
∴△CEF≌△DCO(AAS),
∴CF=OD=2,
∴OA=OD+AD=2+6=8,
∴AB=2OA=16.
21.(1)(-6,-2);(2)2;(3)-8
解:(1)过点C作CM⊥x轴于点M,
∵CM⊥OA,AC⊥AB,∠BOA=90°,
∴∠CMA=∠CAB=∠AOB=90°
∴∠MAC+∠OAB=90°,∠OAB +∠OBA=90°,
∴∠MAC=∠OBA,
∵△ABC是以AB为腰的等腰直角三角形,
∴AC=AB,
在△MAC和△OBA中,
,
∴△MAC≌△OBA(AAS),
∴CM=OA=2 ,MA=OB=4,
∴OM=OA+MA=6
∴点C的坐标为(-6,-2);
(2)过点D作DQ⊥OP于Q,
∵DQ⊥OP,DE⊥OE,∠POE=90°,
∴OE=QD,DE=OQ,
∴OP=PQ+OQ=DE+PQ,
∴∠APO+∠QPD=∠APD=90° ∠APO+∠OAP=90°,
∴∠QPD =∠OAP,
∵△APD是以P为直角顶点,AP为腰的等腰直角三角形,
∴AP=PD
在△AOP和△PDQ中,
,
∴△AOP≌△PDQ(AAS),
∴QP=AO=2,
∴OP-DE=PQ=2;
(3)过点F作FS⊥x轴于S,FT⊥y轴于T,
∵F(-4,-4),
∴FS=FT=4,
∵FT⊥y轴,SH⊥y轴
∴∠FHS=∠HFT,
∵∠FGT+∠GFT=∠HFT+∠GFT=90°,
∴∠FHS=∠HFT=∠FGT,
在△FSH和△FTG中,
,
∴△FSH≌△FTG(AAS)
∴GT=HS,
又∵G(0,m),H(n,0),点F坐标为(-4,-4)
∴OT=OS=4,OG=-m,OH=n,
∴GT=OG-OT=-m-4, HS=OH+OS=n+4,
∴-m-4= n+4,
∴m+n=-8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
