鲁教版数学七年级下册 9.2频率的稳定性 课件(共27张PPT)
文档属性
| 名称 | 鲁教版数学七年级下册 9.2频率的稳定性 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-23 10:51:19 | ||
图片预览






文档简介
(共27张PPT)
9.2频率的稳定性(2)
第九章 概率初步
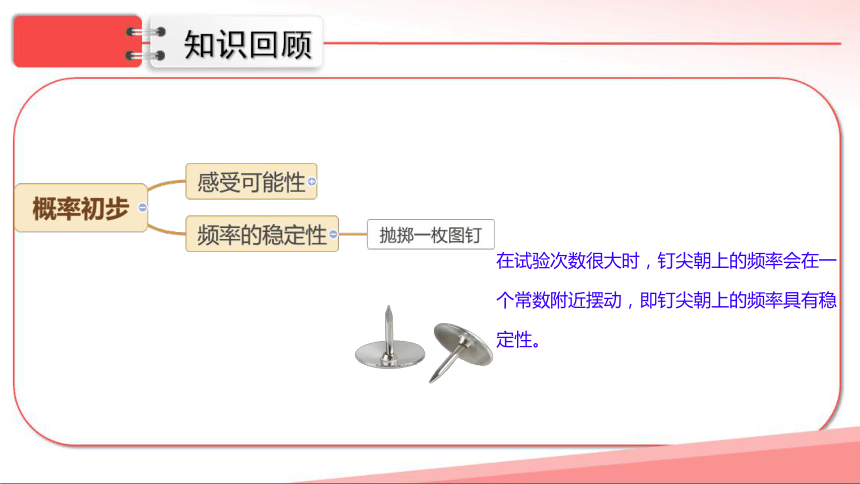
在试验次数很大时,钉尖朝上的频率会在一个常数附近摆动,即钉尖朝上的频率具有稳定性。
抛掷一枚均匀的硬币,硬币落下后,会出现几种情况?
你认为正面朝上和正面朝下的可能性相同吗
1. 通过试验,理解当实验次数较大时,估计出某一事件发生的频率具有稳定性。
2.了解概率的定义。
3.学会根据实际问题的特点,用频率来估计事件发生的概率,培养分析问题,解决问题的能力。
知 识 性 评 价 评价任务 熟练 掌握 知道
任 务 一 同桌两人能够安全、准确的完成抛硬币游戏任务,记录数据。
能快速、准确的统计全班的试验数据,并求出相对应的频率。
通过观察折线统计图,能够积极的思考并参与讨论得出相关的规律。
能够归纳总结试验次数很大时,事件发生频率具有稳定性和概率的定义。
(1) 同桌两人做20次抛掷硬币的游戏,一人掷硬币一人记录,用“正”记录,用数字表示次数记录表格中,并完成表格。
注意:抛掷硬币时,要从一定的高度任意地抛出,以保证试验的随机性;要把硬币扔到盒中,扔到盒外需要重新投掷。
试验总次数n "正“字记录 20
正面朝上的次数m1
正面朝下的次数m2
正面朝上的频率
正面朝下的频率
(2)统计全班同学的试验结果, 并将试验数据汇总填入下表:
组别 1 2 3 4 5 6 7 8 9 10
试验次数 20 20 20 20 20 20 20 20 20 20
正面朝上的次数
正面朝上的频率
正面朝下的次数
正面朝下的频率
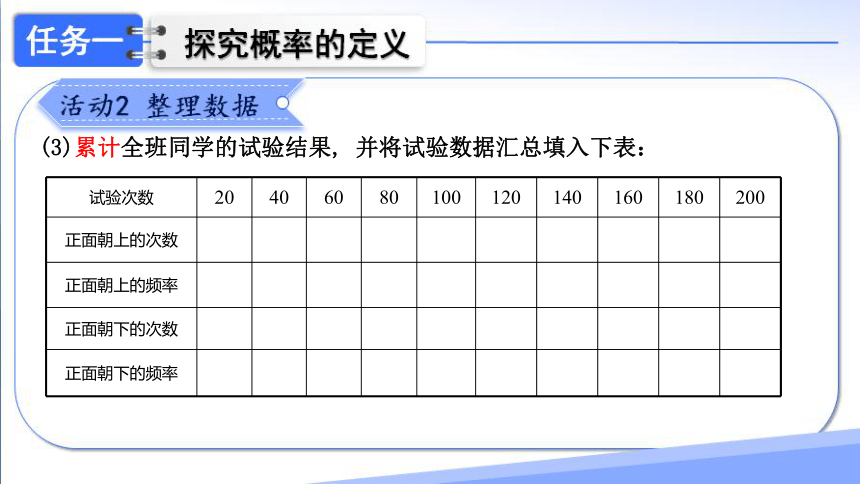
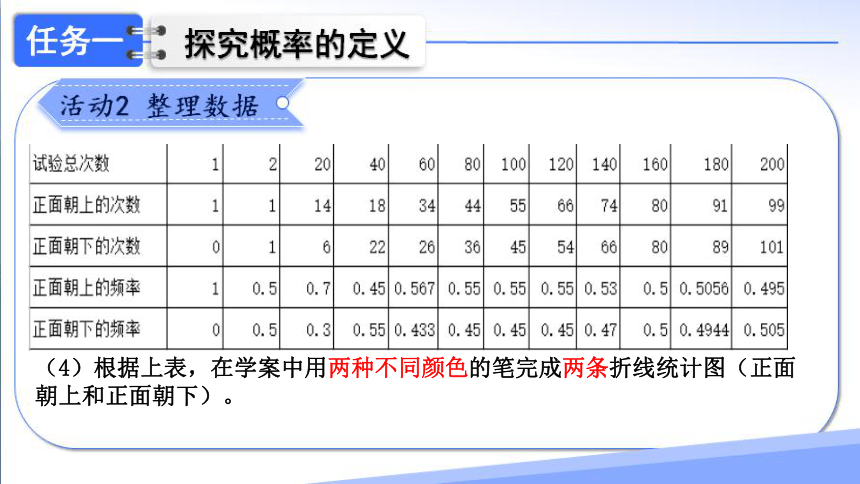
(3)累计全班同学的试验结果, 并将试验数据汇总填入下表:
试验次数 20 40 60 80 100 120 140 160 180 200
正面朝上的次数
正面朝上的频率
正面朝下的次数
正面朝下的频率
(4)根据上表,在学案中用两种不同颜色的笔完成两条折线统计图(正面朝上和正面朝下)。
当试验的次数较小时,折线上下摆动的幅度可能比较大,
随着试验的次数的增加,折线摆动的幅度逐渐变小。
当试验次数很多时, 无论是正面朝上的频率
还是正面朝下的频率,都会稳定在一个常数
(0.5)的附近。
小组合作:
(5)观察折线统计图,你发现了什么规律?
表中的数据支持你发现的规律吗?
无论是抛掷均匀的硬币还是抛掷图钉,在试验次数很大时,
正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
我们把刻画事件A发生的可能性大小的数值,称为事件A发生的概率,记为P(A).
一般的,大量重复的试验中,我们常用随机事件A发生的频率来估计事件A发生的概率.
知 识 性 评 价 评价任务 熟练 掌握 知道
任 务 一 同桌两人能够安全、准确的完成抛硬币游戏任务,记录数据。
能快速、准确的统计全班的试验数据,并求出相对应的频率。
通过观察折线统计图,能够积极的思考并参与讨论得出相关的规律。
能够归纳总结试验次数很大时,事件发生频率具有稳定性和概率的定义。
知 识 性 评 价 评价任务 熟练 掌握 知道
任 务 二 能理解必然事件的概率是1,不可能事件的概率是0,不确定事件的概率在0-1之间
能估计抛掷硬币正面朝上和正面朝下的概率
事件A发生的概率P(A)的取值范围是什么?必然事件发生的概率是多少?不可能事件发生的概率又是多少
必然事件发生的概率为1;不可能事件发生的概率为0;随机事件A发生的概率P(A)是0与1之间的一个常数.
由上面的试验,请你估计抛掷一枚均匀的硬币,正面朝上和正面朝下的概率分别是多少?他们相等吗?
知 识 性 评 价 评价任务 熟练 掌握 知道
任 务 二 能理解必然事件的概率是1,不可能事件的概率是0,不确定事件的概率在0-1之间
会用事件的频率来估计该事件的概率
知 识 性 评 价 评价任务 熟练 掌握 知道
任 务 三 能够了解概率的由来
能正确理解频率与概率的联系与区别
能根据具体情景问题,用频率来估计事件发生的概率
概率主要研究不确定现象,它起源与博弈问题,15-16世纪,意大利数学家们曾讨论过“如果两人赌博提前结束,该如何分配赌金”等问题。比如,两个人做掷硬币游戏,掷出正面甲得1分,掷出反面乙得1分‘先得到10分的人赢得一个大蛋糕。如果游戏因故中途结束此时甲得了8分,乙得了7分,那么他们该如何分配这个蛋糕?
为了回答类似上述问题,人们对不确定现象进行了大量的研究。前面已经列举了历史上一些数学家所做的掷硬币试验的数据。
对不确定现象的研究,最终导致了概率论与数理统计这门学科的出现。它自产生之日起就与人们的实际生活有着紧密的联系,并且解决了许多科技发展中的问题。正因为如此,这门学科有着很强的生命力和广阔的发展前景。
1.小凡做了5次抛掷均匀硬币的实验,其中有3次正面朝上,2次正面朝下,他认为正面朝上的概率大约为 ,朝下的概率为 ,你同意他的观点吗?
2.小明抛掷一枚均匀的硬币,正面朝上的概率为 ,那么,抛掷100次硬币,你能保证恰好50次正面朝上吗?
你认为他再多做一些实验,结果还是这样吗?
对某批乒乓球的质量进行随机抽查,如下表所示:
(1)完成上表;
(2)根据上表,在这批乒乓球中任取一个,它为优等品的概率是多少?
0.7
0.86
0.8
0.81
0.82
0.828
0.825
(3)如果重新再抽取1000个乒乓球进行质量检查,对比上表记录下数据,两表结果会一样吗?为什么?
知 识 性 评 价 评价任务 熟练 掌握 知道
任 务 三 能够了解概率的由来
能正确理解频率与概率的联系与区别
能根据具体情景问题,用频率来估计事件发生的概率
4.某种麦粒在相同条件下的发芽试验,结果如下表所示:
试验的麦粒数n 100 200 500 1000 2000 5000
发芽的粒数m 94 191 473 954 1906 4748
发芽的概率
任取一粒麦粒,估计它能发芽的概率是 (精确到千分位)
0.94
0.955
0.946
0.954
0.953
0.9496
基础题:
1.小明练习射击共100次,其中有90次击中靶子,
由此可估计,小明射击一次击中靶子的概是( )
A.0.9 B 0.6 C. 0.4 D. 无法确定
2.今天是星期天,昨天必定是星期六的概率是
3.小明步行的速度是每小时40千米的概率是
拓展题:
4.掷一枚均匀的骰子。
(1)会出现哪些可能的结果?
(2)掷出点数为1与掷出点数为2的可能性相同吗?掷出点数为1与掷出点数为3的可能性相同吗?
(3)每个出现的可能性相同吗?你是怎样做的?
评价标准 自我评价
A(能独立解决所有问题并帮助小组成员解疑答惑)
B(大部分的题目能独立完成,1至2道题目有困难,但通过课堂讲解已掌握,如 )
C(1至2道题目能独立完成,其他题目有困难但通过课堂讲解已解决如 )
D(大部分题目无法听懂,还存留很多疑惑,如 )
A
1
0
0.950
1,2,3,4,5,6
相同
相同
相同
通过本节课的学习,有什么收获?
有什么疑惑?
实践性作业:
设计一个转盘,通过试验的方法求中一等奖的概率
基础作业:
完成学案对应课时的基础作业。
9.2频率的稳定性(2)
第九章 概率初步
在试验次数很大时,钉尖朝上的频率会在一个常数附近摆动,即钉尖朝上的频率具有稳定性。
抛掷一枚均匀的硬币,硬币落下后,会出现几种情况?
你认为正面朝上和正面朝下的可能性相同吗
1. 通过试验,理解当实验次数较大时,估计出某一事件发生的频率具有稳定性。
2.了解概率的定义。
3.学会根据实际问题的特点,用频率来估计事件发生的概率,培养分析问题,解决问题的能力。
知 识 性 评 价 评价任务 熟练 掌握 知道
任 务 一 同桌两人能够安全、准确的完成抛硬币游戏任务,记录数据。
能快速、准确的统计全班的试验数据,并求出相对应的频率。
通过观察折线统计图,能够积极的思考并参与讨论得出相关的规律。
能够归纳总结试验次数很大时,事件发生频率具有稳定性和概率的定义。
(1) 同桌两人做20次抛掷硬币的游戏,一人掷硬币一人记录,用“正”记录,用数字表示次数记录表格中,并完成表格。
注意:抛掷硬币时,要从一定的高度任意地抛出,以保证试验的随机性;要把硬币扔到盒中,扔到盒外需要重新投掷。
试验总次数n "正“字记录 20
正面朝上的次数m1
正面朝下的次数m2
正面朝上的频率
正面朝下的频率
(2)统计全班同学的试验结果, 并将试验数据汇总填入下表:
组别 1 2 3 4 5 6 7 8 9 10
试验次数 20 20 20 20 20 20 20 20 20 20
正面朝上的次数
正面朝上的频率
正面朝下的次数
正面朝下的频率
(3)累计全班同学的试验结果, 并将试验数据汇总填入下表:
试验次数 20 40 60 80 100 120 140 160 180 200
正面朝上的次数
正面朝上的频率
正面朝下的次数
正面朝下的频率
(4)根据上表,在学案中用两种不同颜色的笔完成两条折线统计图(正面朝上和正面朝下)。
当试验的次数较小时,折线上下摆动的幅度可能比较大,
随着试验的次数的增加,折线摆动的幅度逐渐变小。
当试验次数很多时, 无论是正面朝上的频率
还是正面朝下的频率,都会稳定在一个常数
(0.5)的附近。
小组合作:
(5)观察折线统计图,你发现了什么规律?
表中的数据支持你发现的规律吗?
无论是抛掷均匀的硬币还是抛掷图钉,在试验次数很大时,
正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
我们把刻画事件A发生的可能性大小的数值,称为事件A发生的概率,记为P(A).
一般的,大量重复的试验中,我们常用随机事件A发生的频率来估计事件A发生的概率.
知 识 性 评 价 评价任务 熟练 掌握 知道
任 务 一 同桌两人能够安全、准确的完成抛硬币游戏任务,记录数据。
能快速、准确的统计全班的试验数据,并求出相对应的频率。
通过观察折线统计图,能够积极的思考并参与讨论得出相关的规律。
能够归纳总结试验次数很大时,事件发生频率具有稳定性和概率的定义。
知 识 性 评 价 评价任务 熟练 掌握 知道
任 务 二 能理解必然事件的概率是1,不可能事件的概率是0,不确定事件的概率在0-1之间
能估计抛掷硬币正面朝上和正面朝下的概率
事件A发生的概率P(A)的取值范围是什么?必然事件发生的概率是多少?不可能事件发生的概率又是多少
必然事件发生的概率为1;不可能事件发生的概率为0;随机事件A发生的概率P(A)是0与1之间的一个常数.
由上面的试验,请你估计抛掷一枚均匀的硬币,正面朝上和正面朝下的概率分别是多少?他们相等吗?
知 识 性 评 价 评价任务 熟练 掌握 知道
任 务 二 能理解必然事件的概率是1,不可能事件的概率是0,不确定事件的概率在0-1之间
会用事件的频率来估计该事件的概率
知 识 性 评 价 评价任务 熟练 掌握 知道
任 务 三 能够了解概率的由来
能正确理解频率与概率的联系与区别
能根据具体情景问题,用频率来估计事件发生的概率
概率主要研究不确定现象,它起源与博弈问题,15-16世纪,意大利数学家们曾讨论过“如果两人赌博提前结束,该如何分配赌金”等问题。比如,两个人做掷硬币游戏,掷出正面甲得1分,掷出反面乙得1分‘先得到10分的人赢得一个大蛋糕。如果游戏因故中途结束此时甲得了8分,乙得了7分,那么他们该如何分配这个蛋糕?
为了回答类似上述问题,人们对不确定现象进行了大量的研究。前面已经列举了历史上一些数学家所做的掷硬币试验的数据。
对不确定现象的研究,最终导致了概率论与数理统计这门学科的出现。它自产生之日起就与人们的实际生活有着紧密的联系,并且解决了许多科技发展中的问题。正因为如此,这门学科有着很强的生命力和广阔的发展前景。
1.小凡做了5次抛掷均匀硬币的实验,其中有3次正面朝上,2次正面朝下,他认为正面朝上的概率大约为 ,朝下的概率为 ,你同意他的观点吗?
2.小明抛掷一枚均匀的硬币,正面朝上的概率为 ,那么,抛掷100次硬币,你能保证恰好50次正面朝上吗?
你认为他再多做一些实验,结果还是这样吗?
对某批乒乓球的质量进行随机抽查,如下表所示:
(1)完成上表;
(2)根据上表,在这批乒乓球中任取一个,它为优等品的概率是多少?
0.7
0.86
0.8
0.81
0.82
0.828
0.825
(3)如果重新再抽取1000个乒乓球进行质量检查,对比上表记录下数据,两表结果会一样吗?为什么?
知 识 性 评 价 评价任务 熟练 掌握 知道
任 务 三 能够了解概率的由来
能正确理解频率与概率的联系与区别
能根据具体情景问题,用频率来估计事件发生的概率
4.某种麦粒在相同条件下的发芽试验,结果如下表所示:
试验的麦粒数n 100 200 500 1000 2000 5000
发芽的粒数m 94 191 473 954 1906 4748
发芽的概率
任取一粒麦粒,估计它能发芽的概率是 (精确到千分位)
0.94
0.955
0.946
0.954
0.953
0.9496
基础题:
1.小明练习射击共100次,其中有90次击中靶子,
由此可估计,小明射击一次击中靶子的概是( )
A.0.9 B 0.6 C. 0.4 D. 无法确定
2.今天是星期天,昨天必定是星期六的概率是
3.小明步行的速度是每小时40千米的概率是
拓展题:
4.掷一枚均匀的骰子。
(1)会出现哪些可能的结果?
(2)掷出点数为1与掷出点数为2的可能性相同吗?掷出点数为1与掷出点数为3的可能性相同吗?
(3)每个出现的可能性相同吗?你是怎样做的?
评价标准 自我评价
A(能独立解决所有问题并帮助小组成员解疑答惑)
B(大部分的题目能独立完成,1至2道题目有困难,但通过课堂讲解已掌握,如 )
C(1至2道题目能独立完成,其他题目有困难但通过课堂讲解已解决如 )
D(大部分题目无法听懂,还存留很多疑惑,如 )
A
1
0
0.950
1,2,3,4,5,6
相同
相同
相同
通过本节课的学习,有什么收获?
有什么疑惑?
实践性作业:
设计一个转盘,通过试验的方法求中一等奖的概率
基础作业:
完成学案对应课时的基础作业。
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
