人教A版数学选择性必修第二册 4.3.1 等比数列的概念 课件(共32张PPT)
文档属性
| 名称 | 人教A版数学选择性必修第二册 4.3.1 等比数列的概念 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 36.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
等比数列的概念
1.理解等比数列的定义,并能以方程思想作指导,理解和运用它的通项公式.
2.逐步体会类比、归纳的思想,进一步培养概括、抽象思维等能力.
3.培养严密的思维习惯,促进个性品质的良好发展.
学习目标
1
2
3
4
5
终点
起点
第一关 温故知新
等差数列
定义
通项公式
一般地,一个数列从第2项起,每一项与它前一项的差
等于同一个常数.这个数列叫做等差数列。
这个常数叫做等差数列的公差,通常用字母d表示。
等差中项公式
定义表达式:
1
2
3
4
5
终点
第二关 探究新知
请同学们拿出一张纸试一下你最多可以折叠多少次?
有人说:“给我一张足够大的纸,我把它对折,再对折,再对折‥‥‥依次对折50次,那么它的厚度可以让我在地球和月球之间建一座桥”
对折次数 1 2 3 4 5
纸张层数
合作探究等比数列的概念
问题1:观察以上几个数列,类比等差数列,相邻项之间有什么规律吗?
问题2:类比等差数列的概念,你能从上述几个数列的规律中,抽象出等比数列的概念吗?
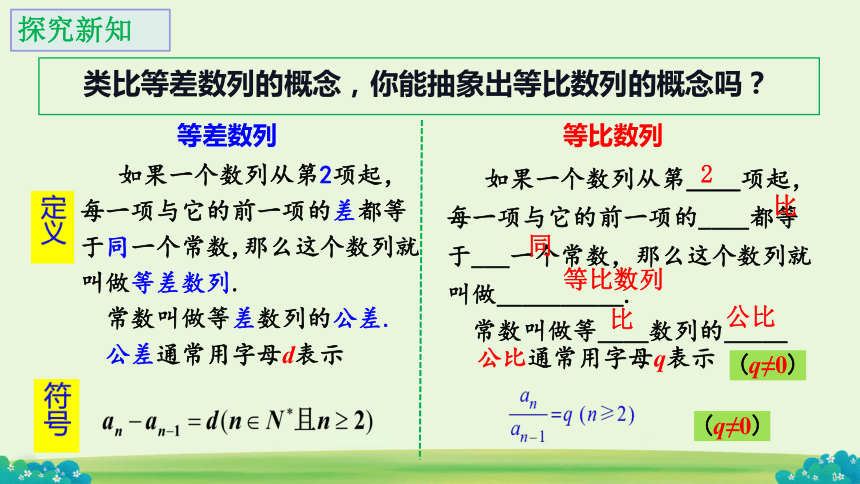
如果一个数列从第____项起,每一项与它的前一项的____都等于___一个常数,那么这个数列就叫做__________.
常数叫做等____数列的_____
等比数列
2
比
同
等比数列
公比
等差数列
如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列.
常数叫做等差数列的公差.
公差通常用字母d表示
公比通常用字母q表示
比
探究新知
类比等差数列的概念,你能抽象出等比数列的概念吗?
(q≠0)
(q≠0)
(1)1,1.1,1.21,1.331,1.4641;
(2)4,-8,16,-32,64,-128;
(3)0,1,0,1;
(4)5,5,5,5,5.
(5)a,a,a,a,a
1.判断下列数列是否为等比数列.如果是,写出公比.
练习
3
A
-3
B
6
C
练习2中间填上什么数,能使三个数构成等比数列?
1,a,9
(二)探究等比中项的概念
2
A
-2
B
0
C
练习2中间填上什么数,能使三个数构成等比数列?
-1,a,-4
(二)探究等比中项的概念
2
A
-2
B
-1.5
C
练习2中间填上什么数,能使三个数构成等比数列?
1,a,-4
(二)探究等比中项的概念
等差中项
等比中项
如果三个数a, A, b组成等差数列,那么A叫做a和b的等差中项.
如果三个数a, G, b组成等比数列,那么G叫做a和b的等比中项.
a, A, b成等差数列
a, G, b成等比数列
探究新知
类比等差中项的概念,你能抽象出等比中项的概念吗?
类比等差数列的通项公式,你能根据等比数列的定义推导它的通项公式吗?
等差数列
等比数列
探究等比数列的通项公式
迭代法
归纳思想
探究:类似于等差数列与一次函数的关系,等比数列可以与哪
类函数建立相似的关系?
等比数列 的第 项 是指数函数
当 时的函数值,
即 .
1、当q>1时,这是什么数列呢?
当0 思考讨论: 等比数列的单调性
3、当q=1时,这是什么数列呢?
4、什么数列既是等差又是等比数列呢?
2、当q<0时,数列各项符号如何呢?这是什么数列呢?
a1>0时,
1
2
3
4
5
终点
第三关 典型例题
典型例题
解:由题意,得
②的两边分别除以①的两边,得
所以
①
②
性质
等比数列的任意一项都可以由该数列的某一项和公比表示.
1
2
3
4
5
终点
第四关 当堂检测
巩固练习
1、
巩固练习
巩固练习
进阶练习:在等比数列{an}中,
(1)a1=3,a3=27,求an;
(2)a2+a5=18,a3+a6=9,an=1,求n.
[感悟]等比数列基本量的求法
a1和q是等比数列的基本量,只要求出这两个基本量,其他量便可求出来,
1
2
3
4
5
终点
第五关 课堂总结
课堂小结
等比数列的概念
1.理解等比数列的定义,并能以方程思想作指导,理解和运用它的通项公式.
2.逐步体会类比、归纳的思想,进一步培养概括、抽象思维等能力.
3.培养严密的思维习惯,促进个性品质的良好发展.
学习目标
1
2
3
4
5
终点
起点
第一关 温故知新
等差数列
定义
通项公式
一般地,一个数列从第2项起,每一项与它前一项的差
等于同一个常数.这个数列叫做等差数列。
这个常数叫做等差数列的公差,通常用字母d表示。
等差中项公式
定义表达式:
1
2
3
4
5
终点
第二关 探究新知
请同学们拿出一张纸试一下你最多可以折叠多少次?
有人说:“给我一张足够大的纸,我把它对折,再对折,再对折‥‥‥依次对折50次,那么它的厚度可以让我在地球和月球之间建一座桥”
对折次数 1 2 3 4 5
纸张层数
合作探究等比数列的概念
问题1:观察以上几个数列,类比等差数列,相邻项之间有什么规律吗?
问题2:类比等差数列的概念,你能从上述几个数列的规律中,抽象出等比数列的概念吗?
如果一个数列从第____项起,每一项与它的前一项的____都等于___一个常数,那么这个数列就叫做__________.
常数叫做等____数列的_____
等比数列
2
比
同
等比数列
公比
等差数列
如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列.
常数叫做等差数列的公差.
公差通常用字母d表示
公比通常用字母q表示
比
探究新知
类比等差数列的概念,你能抽象出等比数列的概念吗?
(q≠0)
(q≠0)
(1)1,1.1,1.21,1.331,1.4641;
(2)4,-8,16,-32,64,-128;
(3)0,1,0,1;
(4)5,5,5,5,5.
(5)a,a,a,a,a
1.判断下列数列是否为等比数列.如果是,写出公比.
练习
3
A
-3
B
6
C
练习2中间填上什么数,能使三个数构成等比数列?
1,a,9
(二)探究等比中项的概念
2
A
-2
B
0
C
练习2中间填上什么数,能使三个数构成等比数列?
-1,a,-4
(二)探究等比中项的概念
2
A
-2
B
-1.5
C
练习2中间填上什么数,能使三个数构成等比数列?
1,a,-4
(二)探究等比中项的概念
等差中项
等比中项
如果三个数a, A, b组成等差数列,那么A叫做a和b的等差中项.
如果三个数a, G, b组成等比数列,那么G叫做a和b的等比中项.
a, A, b成等差数列
a, G, b成等比数列
探究新知
类比等差中项的概念,你能抽象出等比中项的概念吗?
类比等差数列的通项公式,你能根据等比数列的定义推导它的通项公式吗?
等差数列
等比数列
探究等比数列的通项公式
迭代法
归纳思想
探究:类似于等差数列与一次函数的关系,等比数列可以与哪
类函数建立相似的关系?
等比数列 的第 项 是指数函数
当 时的函数值,
即 .
1、当q>1时,这是什么数列呢?
当0
3、当q=1时,这是什么数列呢?
4、什么数列既是等差又是等比数列呢?
2、当q<0时,数列各项符号如何呢?这是什么数列呢?
a1>0时,
1
2
3
4
5
终点
第三关 典型例题
典型例题
解:由题意,得
②的两边分别除以①的两边,得
所以
①
②
性质
等比数列的任意一项都可以由该数列的某一项和公比表示.
1
2
3
4
5
终点
第四关 当堂检测
巩固练习
1、
巩固练习
巩固练习
进阶练习:在等比数列{an}中,
(1)a1=3,a3=27,求an;
(2)a2+a5=18,a3+a6=9,an=1,求n.
[感悟]等比数列基本量的求法
a1和q是等比数列的基本量,只要求出这两个基本量,其他量便可求出来,
1
2
3
4
5
终点
第五关 课堂总结
课堂小结
