教科版选修3-4第一章机械振动 1.2单摆 课件(共20张PPT)
文档属性
| 名称 | 教科版选修3-4第一章机械振动 1.2单摆 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 665.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-04-23 00:00:00 | ||
图片预览




文档简介
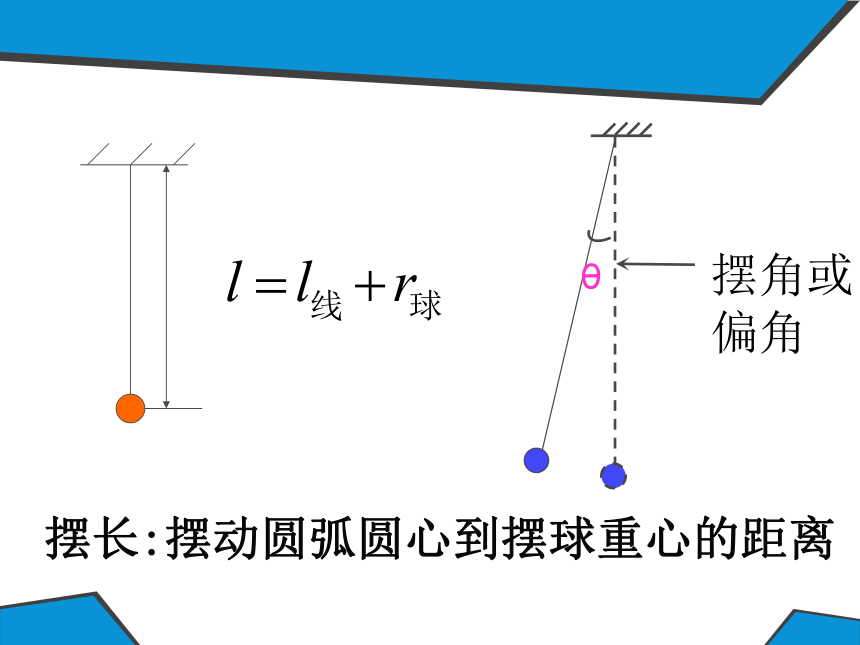
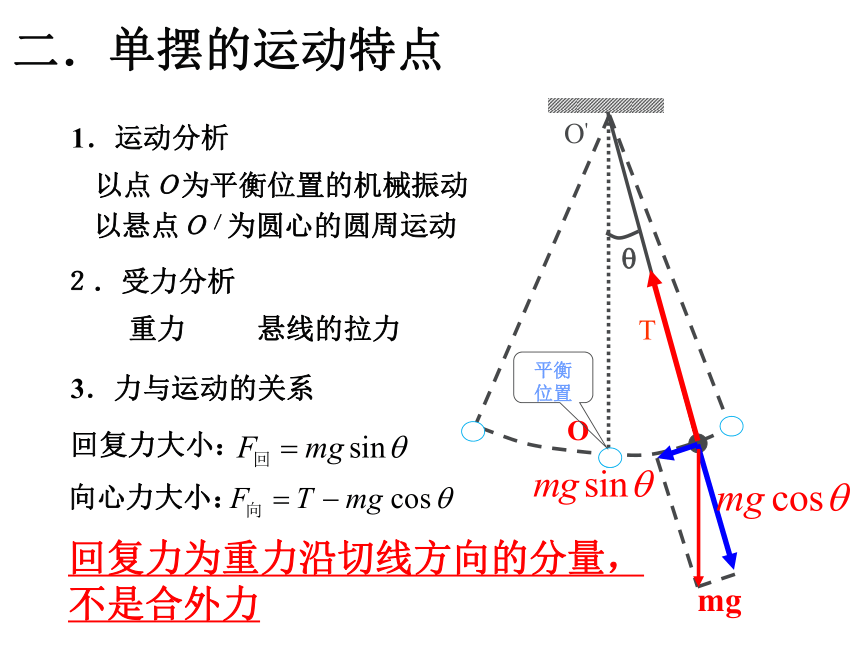
课件20张PPT。 小明家从广州搬到了北京,搬家时把家里的摆钟也带去了。过了几天之后,小明发现摆钟的时间不准确了。校准后,过了几天又出现相同的情况,你知道这是为什么吗?摆钟怎么了?单摆?L线>>D球(小球看成质点)?m线<不是合外力回复力: F=mg sinθ
(重力沿切线方向的分量)
那么,单摆在竖直平面的摆动是不是机械振动中最简单的简谐运动呢?简谐运动 F=-kX
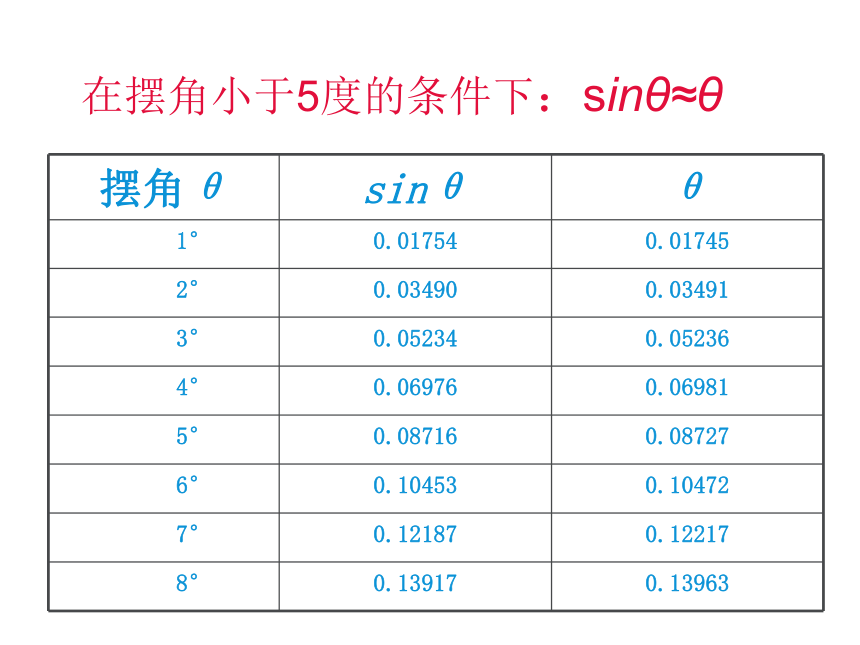
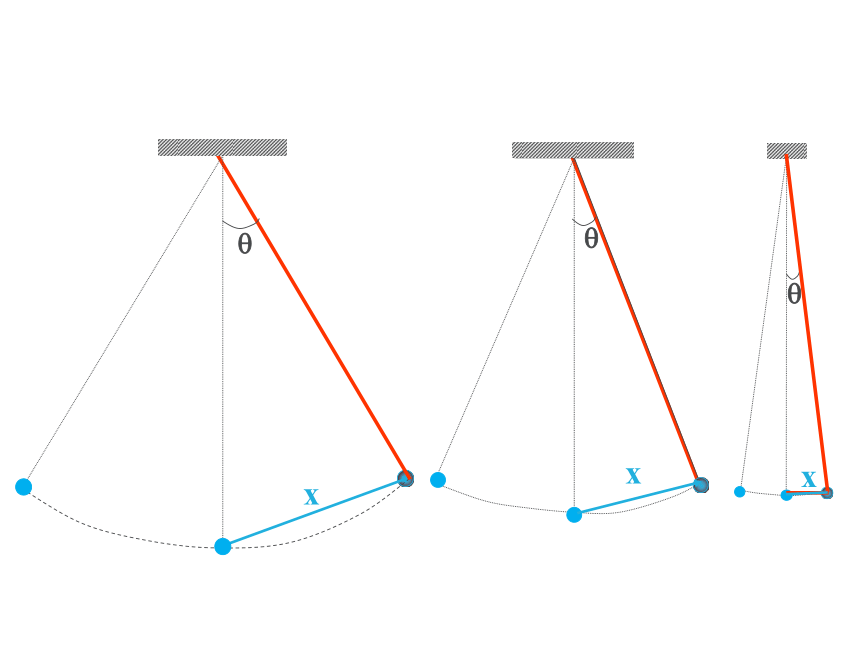
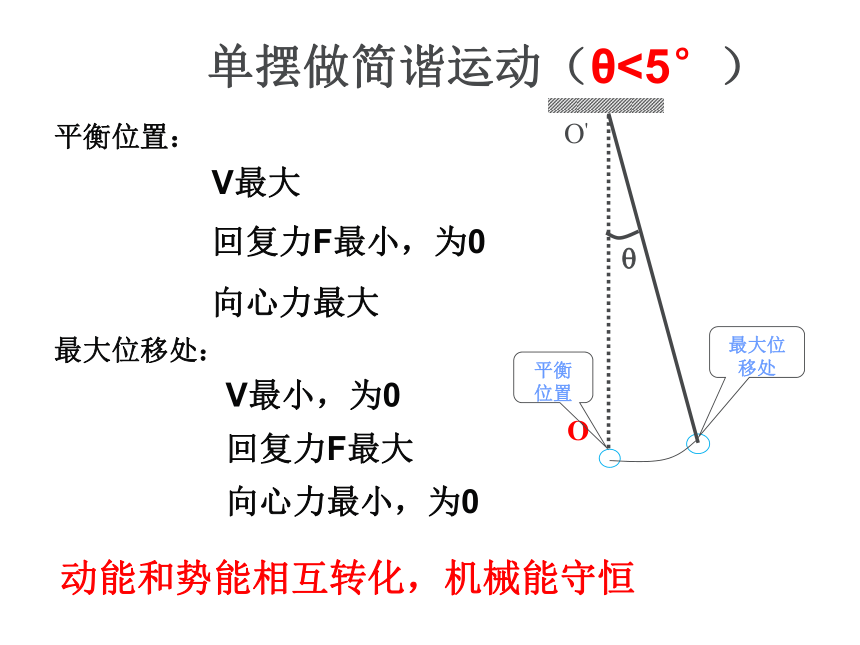
=-kX?在摆角小于5度的条件下:sinθ≈θL位移方向与回复力方向相反F回=-kx 当θ很小时, sin θ ≈ θ, x ≈弧长=L θ结论:当最大摆角很小时(θ< 5° ),单摆在竖直面内的摆动可看作是简谐运动。单摆做简谐运动(θ<5°)平衡位置:最大位移处:动能和势能相互转化,机械能守恒OO'?平衡位置最大位移处V最大回复力F最小,为0向心力最大V最小,为0回复力F最大向心力最小,为0描述简谐运动特征的物理量:振幅 周期 频率周期公式: 摆角很小的情况下,单摆做简谐运动的振动周期跟摆长的平方根成正比,跟重力加速度的平方根成反比。与振幅、摆球质量无关。单位:秒(s)2.单摆周期公式: 摆长、重力加速度都一定时,周期和频率也一定,通常称为单摆的固有周期和固有频率。蛇摆 小明家从广州搬到了北京,搬家时把家里的摆钟也带去了。过了几天之后,小明发现摆钟的时间不准确了。校准后,过了几天又出现相同的情况,你知道这是为什么吗?摆钟变快还是变慢了?该怎么调整?摆钟怎么了?变快加长摆长例题1:一个单摆,周期是T,
a. 如果摆球质量增到2倍,周期将
b. 如果摆的振幅增到2倍,周期将
c. 如果摆长增到4倍,周期将
d. 如果将单摆从赤道移到北京,周期将
e. 如果将单摆从海面移到高山,周期将 变大变为两倍不变不变变小 2.悬挂于同一点的两个单摆的摆长相等,A的质量大于B的质量,O为平衡位置,分别把它们拉离平衡位置同时释放,若最大的摆角都小于5°,那么它们将相遇在( )
A. O 点
B. O点左侧
C. O点右侧
D. 无法确定A课堂练习:五 单摆的应用1.利用它的等时性计时2.测定重力加速度惠更斯在1656年首先利用摆的等时性原理制成了第一座摆钟3.秒摆T=2S小 结1、单摆的理想化模型:
在细线的一端拴上一个小球,另一端固定在悬点上,如果线的伸缩和质量可以忽略不计,球的直径比线长短得多。
2、单摆运动的性质:
在摆角? < 5°的条件下,单摆的振动可看作简谐振动。
3、单摆振动的周期公式
单摆周期与摆长和重力加速度有关,与振幅和质量无关。L双线摆设光滑圆弧槽的半径为R,小球半径为r,摆角小于5°,求周期。等效摆长:等效摆长:例题3:如图所示,摆长为L的单摆,原来的周期为T。
现在在悬点O的正下方A点固定一颗钉子,OA=5L/9,
令单摆由平衡位置向左摆动时以A为悬点作简谐振动,
则这个摆完成一次全振动所需的时间是 。5T/6②等效重力加速度 不论悬点如何运动或还是受别的作用力,等效重力加速度的取值总是单摆不振动时,摆线的拉力与摆球质量的比值(g=T/m)。
(重力沿切线方向的分量)
那么,单摆在竖直平面的摆动是不是机械振动中最简单的简谐运动呢?简谐运动 F=-kX
=-kX?在摆角小于5度的条件下:sinθ≈θL位移方向与回复力方向相反F回=-kx 当θ很小时, sin θ ≈ θ, x ≈弧长=L θ结论:当最大摆角很小时(θ< 5° ),单摆在竖直面内的摆动可看作是简谐运动。单摆做简谐运动(θ<5°)平衡位置:最大位移处:动能和势能相互转化,机械能守恒OO'?平衡位置最大位移处V最大回复力F最小,为0向心力最大V最小,为0回复力F最大向心力最小,为0描述简谐运动特征的物理量:振幅 周期 频率周期公式: 摆角很小的情况下,单摆做简谐运动的振动周期跟摆长的平方根成正比,跟重力加速度的平方根成反比。与振幅、摆球质量无关。单位:秒(s)2.单摆周期公式: 摆长、重力加速度都一定时,周期和频率也一定,通常称为单摆的固有周期和固有频率。蛇摆 小明家从广州搬到了北京,搬家时把家里的摆钟也带去了。过了几天之后,小明发现摆钟的时间不准确了。校准后,过了几天又出现相同的情况,你知道这是为什么吗?摆钟变快还是变慢了?该怎么调整?摆钟怎么了?变快加长摆长例题1:一个单摆,周期是T,
a. 如果摆球质量增到2倍,周期将
b. 如果摆的振幅增到2倍,周期将
c. 如果摆长增到4倍,周期将
d. 如果将单摆从赤道移到北京,周期将
e. 如果将单摆从海面移到高山,周期将 变大变为两倍不变不变变小 2.悬挂于同一点的两个单摆的摆长相等,A的质量大于B的质量,O为平衡位置,分别把它们拉离平衡位置同时释放,若最大的摆角都小于5°,那么它们将相遇在( )
A. O 点
B. O点左侧
C. O点右侧
D. 无法确定A课堂练习:五 单摆的应用1.利用它的等时性计时2.测定重力加速度惠更斯在1656年首先利用摆的等时性原理制成了第一座摆钟3.秒摆T=2S小 结1、单摆的理想化模型:
在细线的一端拴上一个小球,另一端固定在悬点上,如果线的伸缩和质量可以忽略不计,球的直径比线长短得多。
2、单摆运动的性质:
在摆角? < 5°的条件下,单摆的振动可看作简谐振动。
3、单摆振动的周期公式
单摆周期与摆长和重力加速度有关,与振幅和质量无关。L双线摆设光滑圆弧槽的半径为R,小球半径为r,摆角小于5°,求周期。等效摆长:等效摆长:例题3:如图所示,摆长为L的单摆,原来的周期为T。
现在在悬点O的正下方A点固定一颗钉子,OA=5L/9,
令单摆由平衡位置向左摆动时以A为悬点作简谐振动,
则这个摆完成一次全振动所需的时间是 。5T/6②等效重力加速度 不论悬点如何运动或还是受别的作用力,等效重力加速度的取值总是单摆不振动时,摆线的拉力与摆球质量的比值(g=T/m)。
同课章节目录
- 第一章 机械振动
- 1 简谐运动
- 2 单摆
- 3 简谐运动的图像和公式
- 4 阻尼振动 受迫振动
- 5 实验探究:用单摆测定重力加速度
- 第二章 机械波
- 1 机械波的形成和传播
- 2 横波的图像
- 3 波的频率和波速
- 4 惠更新原理 波的反射与折射
- 5 波的干射 衍射
- 6 多普勒效应
- 第三章 电磁振荡 电磁波
- 1 电磁振荡
- 2 电磁场和电磁波
- 3 电磁波谱 电磁波的应用
- 4 无线电波的发射、传播和接收
- 第四章 光的折射
- 1 光的折射定律
- 2 实验探究:测定玻璃的折射率
- 3 光的全反射
- 第五章 光的波动性
- 1 光的干涉
- 2 实验探究:用双缝干涉油光的波长
- 3 光的衍射与偏振
- 4 激光
- 第六章 相对论
- 1 经典时空观
- 2 狭义对相对论的两个基本假设
- 3 相对论时空观
- 4 相对论的速度变换定律 质量和能量的关系
- 5 广义相对论
