2.4.2 平面向量数量积的坐标表示、模、夹角
文档属性
| 名称 | 2.4.2 平面向量数量积的坐标表示、模、夹角 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-23 00:00:00 | ||
图片预览








文档简介
课件21张PPT。复习引入 我们学过两向量的和与差可以转化为它们相应的坐标来运算,那么怎样用2.4.2 平面向量数量积的坐标表示、模、夹角平面向量数量积的坐标表示
如图,是x轴上的单位向量,是y轴上的单位向量,1 1 0 因为所以下面研究怎样用设两个非零向量 =(x1,y1), =(x2,y2),则
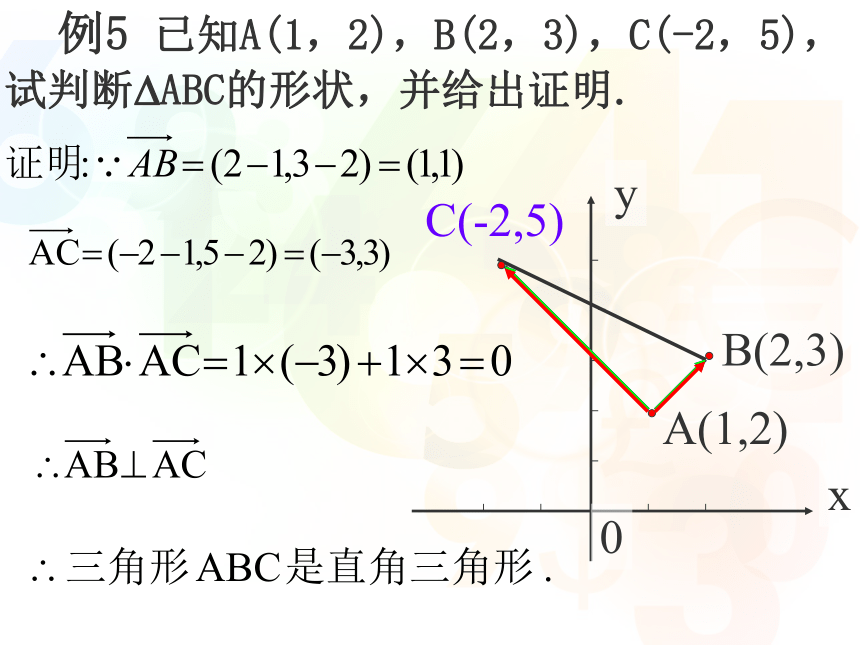
故两个向量的数量积等于它们对应坐标的乘积的和。即 根据平面向量数量积的坐标表示,向量的数量积的运算可转化为向量的坐标运算。向量的模和两点间距离公式:向量垂直和平行的坐标表示:(1)垂直:(2)平行: 例5 已知A(1,2),B(2,3),C(-2,5),试判断?ABC的形状,并给出证明.练习:课本 107页 1,2练习:课本 107页 1,21.已知点A(1,2),B(2,3),C(-2,5),等于( )A.-1 B.0 C.1 D.2B全优60页基础夯实3.已知m=(1,0),n=(1,1),且m+kn恰好与m垂直,则实数k的值是( )
A.1 B.-1 C.1或-1 D.以上皆非B全优60页基础夯实2.若向量a,b的坐标满足a+b=(-2,-1),a-b=(4,-3),则a·b=( )
A.7 B.5 C.-5 D.-1C【解析】∵a+b=(-2,-1),a-b=(4,-3),∴a=(1,-2),b=(-3,1),∴a·b=-5.【例3】 已知A(2,1),B(3,2),D(-1,4).(1)【证明】由已知,得全优60页典例剖析【例3】 已知A(2,1),B(3,2),D(-1,4).全优60页典例剖析(2)若四边形ABCD是矩形,试确定点C的坐标;(2)解:设C(x,y),(-3,3)=(x-3,y-2),所以C(0,5).4.(2014年江西)已知单位向量e1,e2的夹角为α且若向量a=3e1-2e2,则|a|=________.3【解析】由向量数量积的定义知e1·e2=|e1||e2|cos α而a2=(3e1-2e2)2=9e12-12e1·e2+4e22所以|a|=3.全优93页限时规范训练向量夹角公式的坐标表示: 例6:设 a =( 5,-7),b=( -6,-4 ),求 a·b 及a、b间的夹角θ(精确到1°).解:≈-0.0322413θ≈-92°2.设a=(-1,1),b=(4,3),c=(5,-2).求:(1)a与b的夹角的余弦值;【解析】(1)设a与b的夹角为θ,故a与b的夹角的余弦值为全优60页变式训练2.设a=(-1,1),b=(4,3),c=(5,-2).求:【解析】全优60页变式训练(2)c在a方向上的投影;(2)设a与c的夹角为α,所以c在a方向上的投影为|c|cos α2.设a=(-1,1),b=(4,3),c=(5,-2).求:【解析】全优60页变式训练(3)λ1和λ2,使c=λ1a+λ2b.(3)因为c=λ1a+λ2b,5.已知a,b为平面向量且a=(4,3),2a+b=(3,18),求a,b夹角的余弦值.【解析】由已知,得b=(3,18)-2a=(3,18)-(8,6)=(-5,12),所以a,b夹角的余弦值为全优93页限时规范训练
如图,是x轴上的单位向量,是y轴上的单位向量,1 1 0 因为所以下面研究怎样用设两个非零向量 =(x1,y1), =(x2,y2),则
故两个向量的数量积等于它们对应坐标的乘积的和。即 根据平面向量数量积的坐标表示,向量的数量积的运算可转化为向量的坐标运算。向量的模和两点间距离公式:向量垂直和平行的坐标表示:(1)垂直:(2)平行: 例5 已知A(1,2),B(2,3),C(-2,5),试判断?ABC的形状,并给出证明.练习:课本 107页 1,2练习:课本 107页 1,21.已知点A(1,2),B(2,3),C(-2,5),等于( )A.-1 B.0 C.1 D.2B全优60页基础夯实3.已知m=(1,0),n=(1,1),且m+kn恰好与m垂直,则实数k的值是( )
A.1 B.-1 C.1或-1 D.以上皆非B全优60页基础夯实2.若向量a,b的坐标满足a+b=(-2,-1),a-b=(4,-3),则a·b=( )
A.7 B.5 C.-5 D.-1C【解析】∵a+b=(-2,-1),a-b=(4,-3),∴a=(1,-2),b=(-3,1),∴a·b=-5.【例3】 已知A(2,1),B(3,2),D(-1,4).(1)【证明】由已知,得全优60页典例剖析【例3】 已知A(2,1),B(3,2),D(-1,4).全优60页典例剖析(2)若四边形ABCD是矩形,试确定点C的坐标;(2)解:设C(x,y),(-3,3)=(x-3,y-2),所以C(0,5).4.(2014年江西)已知单位向量e1,e2的夹角为α且若向量a=3e1-2e2,则|a|=________.3【解析】由向量数量积的定义知e1·e2=|e1||e2|cos α而a2=(3e1-2e2)2=9e12-12e1·e2+4e22所以|a|=3.全优93页限时规范训练向量夹角公式的坐标表示: 例6:设 a =( 5,-7),b=( -6,-4 ),求 a·b 及a、b间的夹角θ(精确到1°).解:≈-0.0322413θ≈-92°2.设a=(-1,1),b=(4,3),c=(5,-2).求:(1)a与b的夹角的余弦值;【解析】(1)设a与b的夹角为θ,故a与b的夹角的余弦值为全优60页变式训练2.设a=(-1,1),b=(4,3),c=(5,-2).求:【解析】全优60页变式训练(2)c在a方向上的投影;(2)设a与c的夹角为α,所以c在a方向上的投影为|c|cos α2.设a=(-1,1),b=(4,3),c=(5,-2).求:【解析】全优60页变式训练(3)λ1和λ2,使c=λ1a+λ2b.(3)因为c=λ1a+λ2b,5.已知a,b为平面向量且a=(4,3),2a+b=(3,18),求a,b夹角的余弦值.【解析】由已知,得b=(3,18)-2a=(3,18)-(8,6)=(-5,12),所以a,b夹角的余弦值为全优93页限时规范训练
