6.2.2排列数 课件(共29张PPT)
文档属性
| 名称 | 6.2.2排列数 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
6.2.2 排列数
学习目标
1.能利用计数原理推导排列数公式,并掌握排列数公式及
其变形.
2.能正确运用排列数公式进行相关计算.
3.掌握几种有限制条件的排列,能应用排列数公式解决简
单的实际问题.
4.通过排列数公式的学习,提升数学运算的素养.
复习引入
一般地,从n个不同元素中取出m(m≤n)个元素,并_________________
排成一列,叫做从n个不同元素中取出m个元素的一个排列.
1.排列的定义:
2.排列问题的判断方法:
(1)元素的无重复性;
(2)元素的有序性.
判断关键是看选出的元素有没有顺序要求.
2. 分步乘法计数原理:
一般地,完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N= 种不同的方法.
一般地,如果完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法, ,做第n步有mn种不同的方法,那么完成这件事共有N= 种不同的方法.
复习引入
新知引入
思考:研究一个排列问题,往往只需知道所有排列的个数而无需一一写出所有的排列,那么能否不通过一一写出所有的排列而直接“得”出所有排列的个数呢?
新知学习
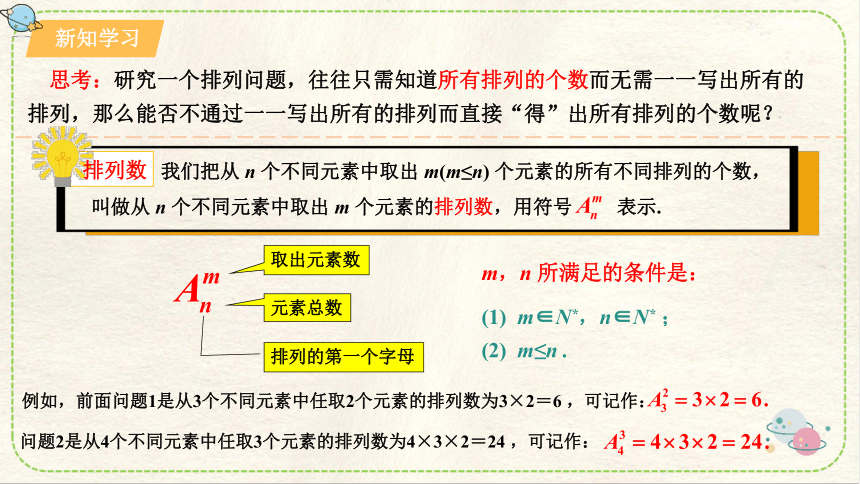
排列数
我们把从 n 个不同元素中取出 m(m≤n) 个元素的所有不同排列的个数,
叫做从 n 个不同元素中取出 m 个元素的排列数,用符号 表示.
排列的第一个字母
元素总数
取出元素数
m,n 所满足的条件是:
(1) m∈N*,n∈N* ;
(2) m≤n .
例如,前面问题1是从3个不同元素中任取2个元素的排列数为3×2=6 ,可记作:
问题2是从4个不同元素中任取3个元素的排列数为4×3×2=24 ,可记作:
新知引入
新知学习
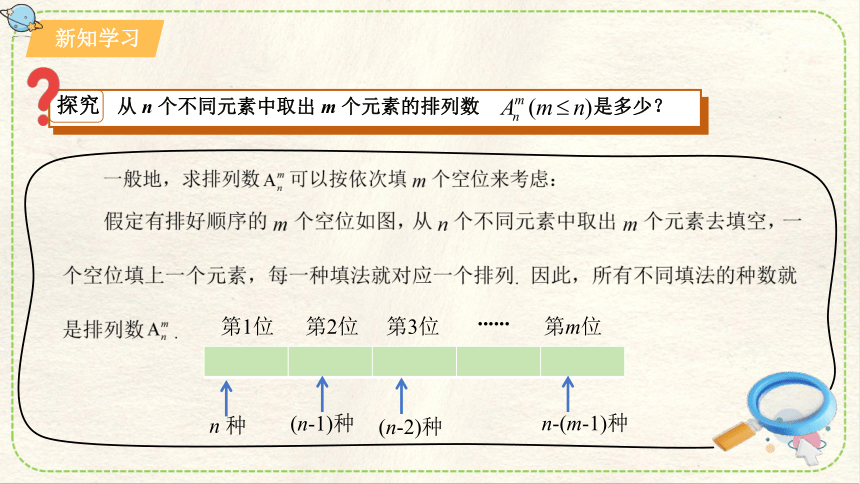
探究
从 n 个不同元素中取出 m 个元素的排列数 是多少?
第1位
第2位
n 种
(n-1)种
新知引入
新知学习
现在来计算有多少种填法. 完成“填空”这件事可以分为两个步骤完成:
第1步,填第1个位置的元素,可以从这n个不同元素中任选1个,有n种选法;
第2步,填第2个位置的元素,可以从剩下的n-1个元素中任选1个,有n-1种选法.
第1位
第2位
第3位
n 种
(n-1)种
(n-2)种
探究
从 n 个不同元素中取出 m 个元素的排列数 是多少?
新知引入
新知学习
n 种
(n-1)种
(n-2)种
n-(m-1)种
第1位
第2位
第3位
第m位
......
探究
从 n 个不同元素中取出 m 个元素的排列数 是多少?
新知引入
新知学习
填空可以分为m个步骤完成:
第1步,从n个不同元素中任选1个填在第1位,有n种选法;
……
探究
从 n 个不同元素中取出 m 个元素的排列数 是多少?
归纳总结
选人不同,结果不同
排列数公式
我们就得到公式
5×4=20
排列数公式的特点:等号右边共m个连续的正整数相乘,其中第一个因数是n,后面每个因数都比前面一个因数少1,即最后一个因数n-m+1.
练一练:
8×7×6=336
新知引入
新知学习
n 的阶乘
例1
新知学习
典例解析
根据排列数公式,可得
新知学习
解:
练习1
计算:
练习2
新知学习
12
新知学习
归纳总结
证明:
排列数公式
的连乘形式
排列数公式
的阶乘形式
排列数公式的阶乘形式
例2
新知学习
典例解析
用0~9这10个数字,可以组成多少个没有重复数字的三位数?
思路点拨
在0~9这10个数字中,因为0不能在百位上,而其他9个数字可以在任意数位上,因此0是一个特殊的元素. 一般地,我们可以从特殊元素的位置入手来考虑问题.)
特殊优先法
典例解析
例2
用0~9这10个数字,可以组成多少个没有重复数字的三位数?
解法一:如图所示,由于三位数的百位上的数字不能是0,所以可以分两步完成:
种
种
百位
十位
个位
特殊位置优先法
新知学习
解法二:如图所示,符合条件的三位数可以分成三类
根据分类加法计数原理,所求的三位数的个数为
百位
十位
个位
0
百位
十位
个位
0
百位
十位
个位
特殊元素优先法
典例解析
例2
用0~9这10个数字,可以组成多少个没有重复数字的三位数?
间接法
新知学习
变式1
用0到9这十个数字,可以组成多少个没有重复数字的三位数且是偶数
解:
0
0
0在个位的有 个;
0在十位的有 个;
没有0的有 个.
∴共有
变式2
新知学习
用0到9这十个数字,可以组成多少个没有重复数字的三位数且是奇数
0
解:
0在十位的有 个;
没有0的有 个.
∴共有
新知学习
知识点拨
(1)直接法:以元素为考察对象,先满足特殊元素的要求,再考虑一般元素(又称为特殊元素优先法);或以位置为考察对象,先满足特殊位置的要求,再考虑一般位置(又称特殊位置优先法).
有限制条件的排列应用题,可以有两种不同的计算方法:
(2)间接法:先不考虑附加条件,计算出总排列数,再减去不合要求的排列数.
练习1
新知学习
一个火车站有8股岔道,如果每股道只能停放1列火车,现要停放4列不同的火车,共有多少种不同的停放方法
解:要停放4列不同的火车,需要从8股岔道上任选4 股岔道,所以不同的停放方法有
课堂小结
2. 全排列数:
1. 排列数公式:
3.阶乘:正整数1到n的连乘积 1×2×···×n称为n的阶乘,用 表示, 即
4.排列数公式的阶乘形式:
随堂练习
C
B
随堂练习
3.有5名同学被安排在周一至周五值日,已知同学甲只能在周一值日,那么5名同学值日顺序的编排方案共有( )
A.12种 B.24种 C.48种 D.120种
解析:∵同学甲只能在周一值日,
∴除同学甲外的4名同学将在周二至周五值日,∴5名同学值日顺序的编排方案共有A=24(种).
B
6
随堂练习
5.植树节这天,某学校组织5名学生依次给树木浇水,其中甲和乙是好朋友,必须相邻,丙不在第三位,则不同的浇水顺序的种数为( )
A.30 B.36 C.40 D.42
C
课时作业
作业
1.《选择性必修第三册》P26“复习巩固” 1、5
2.“综合运用” 8,9
*3.甲、乙、丙、丁、戊共5名同学进行劳动技术比赛,决出第1名到第5名的名次.甲和乙去询问成绩,回答者对甲说:“很遗憾,你和乙都没有得到冠军.”对乙说:“你当然不会是最差的.”从这两个回答分析,5人的名次排列可能有多少种不同情况?
课时作业
*3.甲、乙、丙、丁、戊共5名同学进行劳动技术比赛,决出第1名到第5名的名次.甲和乙去询问成绩,回答者对甲说:“很遗憾,你和乙都没有得到冠军.”对乙说:“你当然不会是最差的.”从这两个回答分析,5人的名次排列可能有多少种不同情况?
解:根据题意,甲乙都没有得到冠军,而乙不是最后一名,分2种情况讨论:
①、甲是最后一名,则乙可以为第二、三、四名,即乙有3种情况,
剩下的三人安排在其他三个名次,有A33 = 6种情况,
此时有3×6=18种名次排列情况;
②、甲不是最后一名,甲乙需要排在第二、三、四名,有A32 = 6种情况,
剩下的三人安排在其他三个名次,有A33 = 6种情况,
此时有6×6=36种名次排列情况;
则一共有36+18=54种不同的名次情况.
6.2.2 排列数
学习目标
1.能利用计数原理推导排列数公式,并掌握排列数公式及
其变形.
2.能正确运用排列数公式进行相关计算.
3.掌握几种有限制条件的排列,能应用排列数公式解决简
单的实际问题.
4.通过排列数公式的学习,提升数学运算的素养.
复习引入
一般地,从n个不同元素中取出m(m≤n)个元素,并_________________
排成一列,叫做从n个不同元素中取出m个元素的一个排列.
1.排列的定义:
2.排列问题的判断方法:
(1)元素的无重复性;
(2)元素的有序性.
判断关键是看选出的元素有没有顺序要求.
2. 分步乘法计数原理:
一般地,完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N= 种不同的方法.
一般地,如果完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法, ,做第n步有mn种不同的方法,那么完成这件事共有N= 种不同的方法.
复习引入
新知引入
思考:研究一个排列问题,往往只需知道所有排列的个数而无需一一写出所有的排列,那么能否不通过一一写出所有的排列而直接“得”出所有排列的个数呢?
新知学习
排列数
我们把从 n 个不同元素中取出 m(m≤n) 个元素的所有不同排列的个数,
叫做从 n 个不同元素中取出 m 个元素的排列数,用符号 表示.
排列的第一个字母
元素总数
取出元素数
m,n 所满足的条件是:
(1) m∈N*,n∈N* ;
(2) m≤n .
例如,前面问题1是从3个不同元素中任取2个元素的排列数为3×2=6 ,可记作:
问题2是从4个不同元素中任取3个元素的排列数为4×3×2=24 ,可记作:
新知引入
新知学习
探究
从 n 个不同元素中取出 m 个元素的排列数 是多少?
第1位
第2位
n 种
(n-1)种
新知引入
新知学习
现在来计算有多少种填法. 完成“填空”这件事可以分为两个步骤完成:
第1步,填第1个位置的元素,可以从这n个不同元素中任选1个,有n种选法;
第2步,填第2个位置的元素,可以从剩下的n-1个元素中任选1个,有n-1种选法.
第1位
第2位
第3位
n 种
(n-1)种
(n-2)种
探究
从 n 个不同元素中取出 m 个元素的排列数 是多少?
新知引入
新知学习
n 种
(n-1)种
(n-2)种
n-(m-1)种
第1位
第2位
第3位
第m位
......
探究
从 n 个不同元素中取出 m 个元素的排列数 是多少?
新知引入
新知学习
填空可以分为m个步骤完成:
第1步,从n个不同元素中任选1个填在第1位,有n种选法;
……
探究
从 n 个不同元素中取出 m 个元素的排列数 是多少?
归纳总结
选人不同,结果不同
排列数公式
我们就得到公式
5×4=20
排列数公式的特点:等号右边共m个连续的正整数相乘,其中第一个因数是n,后面每个因数都比前面一个因数少1,即最后一个因数n-m+1.
练一练:
8×7×6=336
新知引入
新知学习
n 的阶乘
例1
新知学习
典例解析
根据排列数公式,可得
新知学习
解:
练习1
计算:
练习2
新知学习
12
新知学习
归纳总结
证明:
排列数公式
的连乘形式
排列数公式
的阶乘形式
排列数公式的阶乘形式
例2
新知学习
典例解析
用0~9这10个数字,可以组成多少个没有重复数字的三位数?
思路点拨
在0~9这10个数字中,因为0不能在百位上,而其他9个数字可以在任意数位上,因此0是一个特殊的元素. 一般地,我们可以从特殊元素的位置入手来考虑问题.)
特殊优先法
典例解析
例2
用0~9这10个数字,可以组成多少个没有重复数字的三位数?
解法一:如图所示,由于三位数的百位上的数字不能是0,所以可以分两步完成:
种
种
百位
十位
个位
特殊位置优先法
新知学习
解法二:如图所示,符合条件的三位数可以分成三类
根据分类加法计数原理,所求的三位数的个数为
百位
十位
个位
0
百位
十位
个位
0
百位
十位
个位
特殊元素优先法
典例解析
例2
用0~9这10个数字,可以组成多少个没有重复数字的三位数?
间接法
新知学习
变式1
用0到9这十个数字,可以组成多少个没有重复数字的三位数且是偶数
解:
0
0
0在个位的有 个;
0在十位的有 个;
没有0的有 个.
∴共有
变式2
新知学习
用0到9这十个数字,可以组成多少个没有重复数字的三位数且是奇数
0
解:
0在十位的有 个;
没有0的有 个.
∴共有
新知学习
知识点拨
(1)直接法:以元素为考察对象,先满足特殊元素的要求,再考虑一般元素(又称为特殊元素优先法);或以位置为考察对象,先满足特殊位置的要求,再考虑一般位置(又称特殊位置优先法).
有限制条件的排列应用题,可以有两种不同的计算方法:
(2)间接法:先不考虑附加条件,计算出总排列数,再减去不合要求的排列数.
练习1
新知学习
一个火车站有8股岔道,如果每股道只能停放1列火车,现要停放4列不同的火车,共有多少种不同的停放方法
解:要停放4列不同的火车,需要从8股岔道上任选4 股岔道,所以不同的停放方法有
课堂小结
2. 全排列数:
1. 排列数公式:
3.阶乘:正整数1到n的连乘积 1×2×···×n称为n的阶乘,用 表示, 即
4.排列数公式的阶乘形式:
随堂练习
C
B
随堂练习
3.有5名同学被安排在周一至周五值日,已知同学甲只能在周一值日,那么5名同学值日顺序的编排方案共有( )
A.12种 B.24种 C.48种 D.120种
解析:∵同学甲只能在周一值日,
∴除同学甲外的4名同学将在周二至周五值日,∴5名同学值日顺序的编排方案共有A=24(种).
B
6
随堂练习
5.植树节这天,某学校组织5名学生依次给树木浇水,其中甲和乙是好朋友,必须相邻,丙不在第三位,则不同的浇水顺序的种数为( )
A.30 B.36 C.40 D.42
C
课时作业
作业
1.《选择性必修第三册》P26“复习巩固” 1、5
2.“综合运用” 8,9
*3.甲、乙、丙、丁、戊共5名同学进行劳动技术比赛,决出第1名到第5名的名次.甲和乙去询问成绩,回答者对甲说:“很遗憾,你和乙都没有得到冠军.”对乙说:“你当然不会是最差的.”从这两个回答分析,5人的名次排列可能有多少种不同情况?
课时作业
*3.甲、乙、丙、丁、戊共5名同学进行劳动技术比赛,决出第1名到第5名的名次.甲和乙去询问成绩,回答者对甲说:“很遗憾,你和乙都没有得到冠军.”对乙说:“你当然不会是最差的.”从这两个回答分析,5人的名次排列可能有多少种不同情况?
解:根据题意,甲乙都没有得到冠军,而乙不是最后一名,分2种情况讨论:
①、甲是最后一名,则乙可以为第二、三、四名,即乙有3种情况,
剩下的三人安排在其他三个名次,有A33 = 6种情况,
此时有3×6=18种名次排列情况;
②、甲不是最后一名,甲乙需要排在第二、三、四名,有A32 = 6种情况,
剩下的三人安排在其他三个名次,有A33 = 6种情况,
此时有6×6=36种名次排列情况;
则一共有36+18=54种不同的名次情况.
