6.2.4 组合数 课件(共18张PPT)
文档属性
| 名称 | 6.2.4 组合数 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第 六 章 计 数 原 理
6.2.4 组合数
1.通过类比排列数理解组合数的概念.
2.能利用计数原理推导组合数公式.
3. 能用组合数的知识与公式求解相关问题.
问题1:类比排列数,你能说说什么是组合数吗?
组合数
排列数
从个不同的元素中取出个元素的所有不同排列的个数,叫做从个不同的元素中取出个元素的排列数,用符号表示.
从个不同的元素中取出个元素的所有不同组合的个数,叫做从个不同的元素中取出个元素的组合数,用符号表示.
示例:
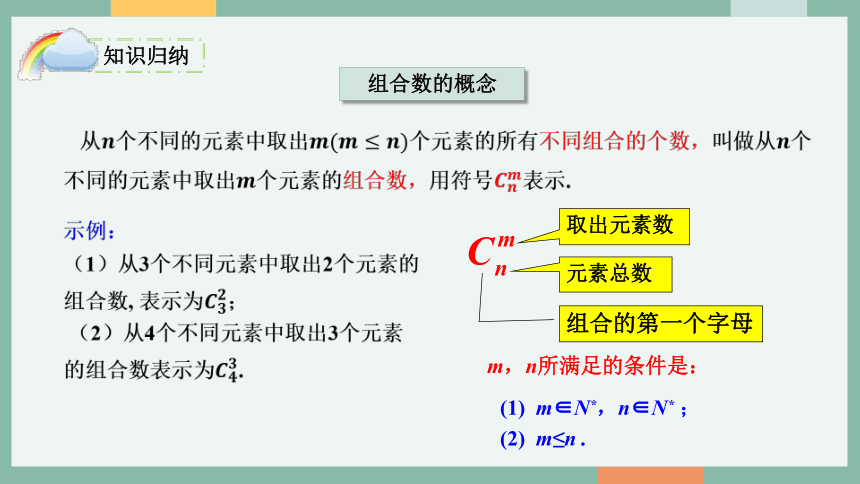
(1)从3个不同元素中取出2个元素的组合数, 表示为;
(2)从4个不同元素中取出3个元素的组合数表示为.
组合的第一个字母
元素总数
取出元素数
m,n所满足的条件是:
(1) m∈N*,n∈N* ;
(2) m≤n .
组合数的概念
知识归纳
从个不同的元素中取出个元素的所有不同组合的个数,叫做从个不同的元素中取出个元素的组合数,用符号表示.
前面,我们利用“元素相同、顺序不同的两个组合相同”“元素相同、顺序不同的两个排列不同”,以“元素相同”为标准,建立了排列和组合之间的对应关系.那它们之间的数量关系是怎样的?
排列数公式:
=?
能否利用组合与排列的关系,由排列数来求组合数呢?
思考
问题2:
(1)3个不同元素a, b, c中取出2个共有几个不同的组合?3个不同元素a, b, c中取出2个元素的排列数为是多少?
(2)4个不同元素a, b, c,d中取出3个共有几个不同的组合?4个不同元素a, b, c,d中取出3个元素的排列数为是多少?
(1)
(2)
下面我们以(2)为例子探究排列数与组合数之间的关系
从4个不同元素中取出3个元素排列数
abc
abd
acd
abc acb bac bca cab cba
abd adb bad bda dab dba
acd adc cad cda dac dca
bcd
bcd bdc cbd cdb dbc dcb
组合
排列
追问: 我们该怎么安排才能和组合联系在一起?
第1步 , 从4个元素中取出3个元素作为一组 , 共有种不同的取法;
第2步, 将取出的3个元素做全排列, 共有种不同的取法.
于是,根据分步乘法计数原理有=
化简后得:
问题3 你能类比“从4个不同元素中取出3个元素排列数”描述“从个元素中取出个元素的排列数”吗?
第1步 , 从n个元素中取出m个元素作为一组 , 共有种不同的取法;
第2步, 将取出的m个元素做全排列, 共有种不同的取法;
于是,根据分步乘法计数原理有
所以
能否用阶乘进行表示?
根据分步乘法计数原理有
这里的,并且,这个公式叫做组合数公式.
又因为
,所以
另外,我们规定 =1.
例6 计算: (1) ; (2) ; (3) ; (4) .
(1) = =120
(2) ===120
(3)
(4) =1
解: 根据组合数公式,可得
追问:仔细观察(1) 和 (2),(3) 和 (4)的结果,你发现了什么?你能否总结归纳出来呢?
例题讲解
所以
性质1 :
性质2:
解:
1. 计算:
计算时,可以通过组合数的性质简化运算.
2. 满足条件 > 的自然数n有( )
C
A. 7个 B. 6个 C. 5个 D. 4个
例7 在100件产品中, 有98件合格品 , 2件次品 . 从这100件产品中任意抽出3件.
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
分析: (1)所求的不同抽法的种数,就是从100件产品中取出3件的组合数;
(2)可以先从2件次品中抽出1件,再从98件合格品中抽出2件,因此可以看作是一个分步完成的组合问题;
(3)从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品的情况,因此可以看作是一个分类完成的组合问题.
例题讲解
解: (1)所有的不同抽法种数,就是从100件产品中抽出3件的组合数,所以抽法种数为
(2)从2件次品中抽出1件次品的抽法有种,从98件合格品中抽出2件合格品的抽法有种,因此抽出的3件中恰好有1件次品的抽法有 (种).
例题讲解
方法2 抽出的3件产品中至少有1件是次品的抽法的种数,就是从100件中抽出3件的抽法种数减去3件中都是合格品的抽法的种数,即
(3)方法1 从100件产品抽出的3件中至少有1件是次品 , 包括有1件次品和有2件次品的情况, 因此根据分类加法计数原理, 抽出的3件产品中至少有1件是次品的抽法的种数为
例题讲解
3.某学校要从5名男教师和3名女教师中随机选出3人去支教,则抽取的3人中,女教师最多为1人的选法种数为( )
A.10 B.30 C.40 D.46
C
从n个不同元素中取出m (m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号表示.
2.组合数公式:
3.组合数性质:
性质1 :
性质2:
1.组合数的概念:
第 六 章 计 数 原 理
6.2.4 组合数
1.通过类比排列数理解组合数的概念.
2.能利用计数原理推导组合数公式.
3. 能用组合数的知识与公式求解相关问题.
问题1:类比排列数,你能说说什么是组合数吗?
组合数
排列数
从个不同的元素中取出个元素的所有不同排列的个数,叫做从个不同的元素中取出个元素的排列数,用符号表示.
从个不同的元素中取出个元素的所有不同组合的个数,叫做从个不同的元素中取出个元素的组合数,用符号表示.
示例:
(1)从3个不同元素中取出2个元素的组合数, 表示为;
(2)从4个不同元素中取出3个元素的组合数表示为.
组合的第一个字母
元素总数
取出元素数
m,n所满足的条件是:
(1) m∈N*,n∈N* ;
(2) m≤n .
组合数的概念
知识归纳
从个不同的元素中取出个元素的所有不同组合的个数,叫做从个不同的元素中取出个元素的组合数,用符号表示.
前面,我们利用“元素相同、顺序不同的两个组合相同”“元素相同、顺序不同的两个排列不同”,以“元素相同”为标准,建立了排列和组合之间的对应关系.那它们之间的数量关系是怎样的?
排列数公式:
=?
能否利用组合与排列的关系,由排列数来求组合数呢?
思考
问题2:
(1)3个不同元素a, b, c中取出2个共有几个不同的组合?3个不同元素a, b, c中取出2个元素的排列数为是多少?
(2)4个不同元素a, b, c,d中取出3个共有几个不同的组合?4个不同元素a, b, c,d中取出3个元素的排列数为是多少?
(1)
(2)
下面我们以(2)为例子探究排列数与组合数之间的关系
从4个不同元素中取出3个元素排列数
abc
abd
acd
abc acb bac bca cab cba
abd adb bad bda dab dba
acd adc cad cda dac dca
bcd
bcd bdc cbd cdb dbc dcb
组合
排列
追问: 我们该怎么安排才能和组合联系在一起?
第1步 , 从4个元素中取出3个元素作为一组 , 共有种不同的取法;
第2步, 将取出的3个元素做全排列, 共有种不同的取法.
于是,根据分步乘法计数原理有=
化简后得:
问题3 你能类比“从4个不同元素中取出3个元素排列数”描述“从个元素中取出个元素的排列数”吗?
第1步 , 从n个元素中取出m个元素作为一组 , 共有种不同的取法;
第2步, 将取出的m个元素做全排列, 共有种不同的取法;
于是,根据分步乘法计数原理有
所以
能否用阶乘进行表示?
根据分步乘法计数原理有
这里的,并且,这个公式叫做组合数公式.
又因为
,所以
另外,我们规定 =1.
例6 计算: (1) ; (2) ; (3) ; (4) .
(1) = =120
(2) ===120
(3)
(4) =1
解: 根据组合数公式,可得
追问:仔细观察(1) 和 (2),(3) 和 (4)的结果,你发现了什么?你能否总结归纳出来呢?
例题讲解
所以
性质1 :
性质2:
解:
1. 计算:
计算时,可以通过组合数的性质简化运算.
2. 满足条件 > 的自然数n有( )
C
A. 7个 B. 6个 C. 5个 D. 4个
例7 在100件产品中, 有98件合格品 , 2件次品 . 从这100件产品中任意抽出3件.
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
分析: (1)所求的不同抽法的种数,就是从100件产品中取出3件的组合数;
(2)可以先从2件次品中抽出1件,再从98件合格品中抽出2件,因此可以看作是一个分步完成的组合问题;
(3)从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品的情况,因此可以看作是一个分类完成的组合问题.
例题讲解
解: (1)所有的不同抽法种数,就是从100件产品中抽出3件的组合数,所以抽法种数为
(2)从2件次品中抽出1件次品的抽法有种,从98件合格品中抽出2件合格品的抽法有种,因此抽出的3件中恰好有1件次品的抽法有 (种).
例题讲解
方法2 抽出的3件产品中至少有1件是次品的抽法的种数,就是从100件中抽出3件的抽法种数减去3件中都是合格品的抽法的种数,即
(3)方法1 从100件产品抽出的3件中至少有1件是次品 , 包括有1件次品和有2件次品的情况, 因此根据分类加法计数原理, 抽出的3件产品中至少有1件是次品的抽法的种数为
例题讲解
3.某学校要从5名男教师和3名女教师中随机选出3人去支教,则抽取的3人中,女教师最多为1人的选法种数为( )
A.10 B.30 C.40 D.46
C
从n个不同元素中取出m (m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号表示.
2.组合数公式:
3.组合数性质:
性质1 :
性质2:
1.组合数的概念:
