6.3.1二项式定理 课件(共26张PPT)
文档属性
| 名称 | 6.3.1二项式定理 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 586.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 22:20:18 | ||
图片预览





文档简介
(共26张PPT)
6.3.1 二项式定理
第 六 章 计 数 原 理
1.能用多项式法则和计数原理推导二项式定理,会用二项式定理
求解二项展开式.
2.理解二项式定理,会利用定理解决与二项式有关的简单问题.
想一想:你还记得什么是二项式吗?
对于a+b,(a+b) ,(a+b) ,(a+b) 等代数式,数学上统称为二项式,其一般形式为:(a+b)n (n∈N*).
在许多代数问题中需要将二项式展开,因此,二项式定理研究的是(a+b)n展开后的表达式的一般结构.那么(a+b)n 的展开式是什么呢
(a+b)2
(a+b)3
那么将(a+b)4 ,(a+b)5 . . .展开后,它们的各项是什么呢?
=C20 a2 + C21 ab+ C22 b2
= C30a3 +C31a2b+C32ab2 +C33 b3
=a3 + 3a2b+3ab2 + b3
= a2 +2ab+b2
我们先来展开下面的式子:
(a+b)2= (a+b) (a+b)
展开后其项的形式为:a2 , ab , b2
这三项的系数为各项在展开式中出现的次数.
考虑b:
每个都不取b的情况有C20 种,则a2前的系数为C20
恰有1个取b的情况有C21种,则ab前的系数为C21
恰有2个取b的情况有C22 种,则b2前的系数为C22
(a+b)2 = a2 +2ab+b2
=C20 a2 + C21 ab+ C22 b2
(a+b)3=a3 + 3a2b+3ab2 + b3
= C30a3 +C31a2b+C32ab2 +C33 b3
对(a+b)2展开式的分析:
a3
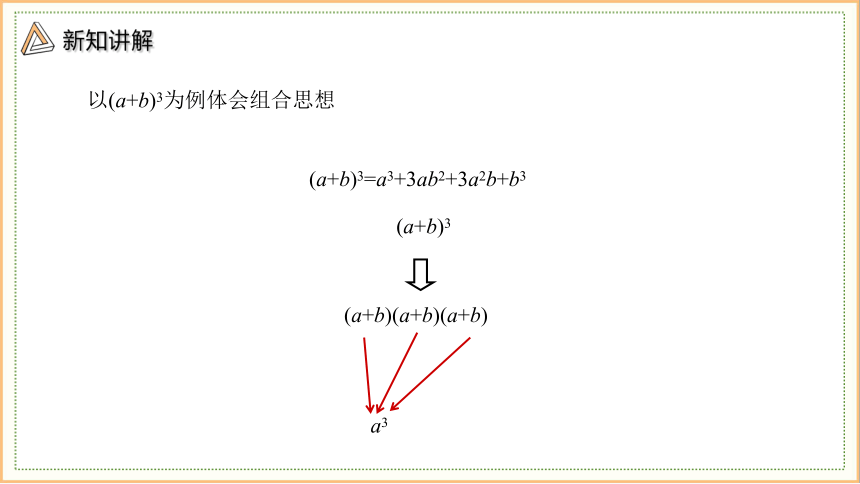
以(a+b)3为例体会组合思想
(a+b)3=a3+3ab2+3a2b+b3
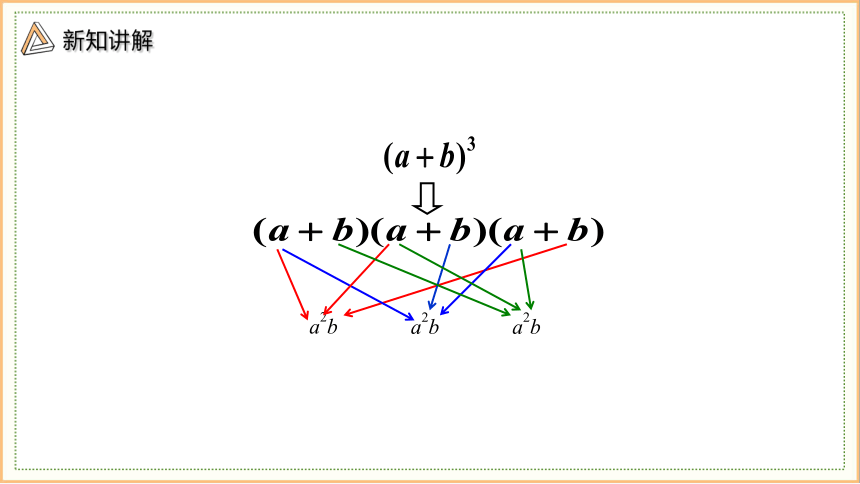
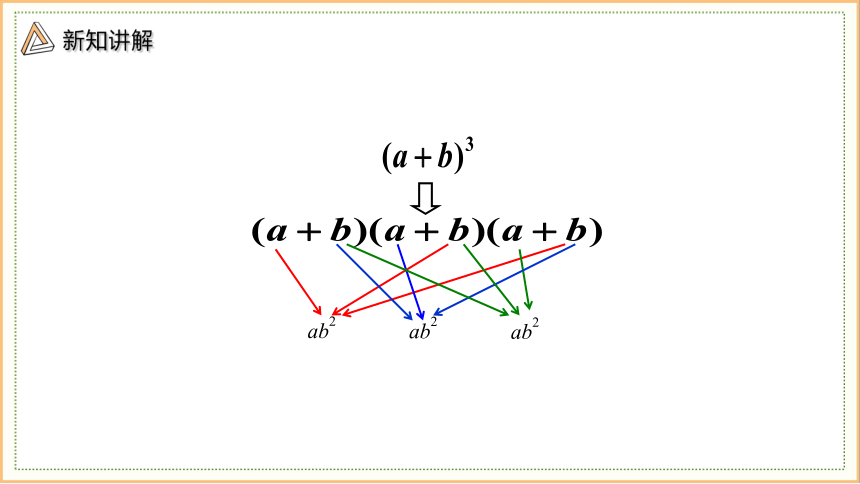
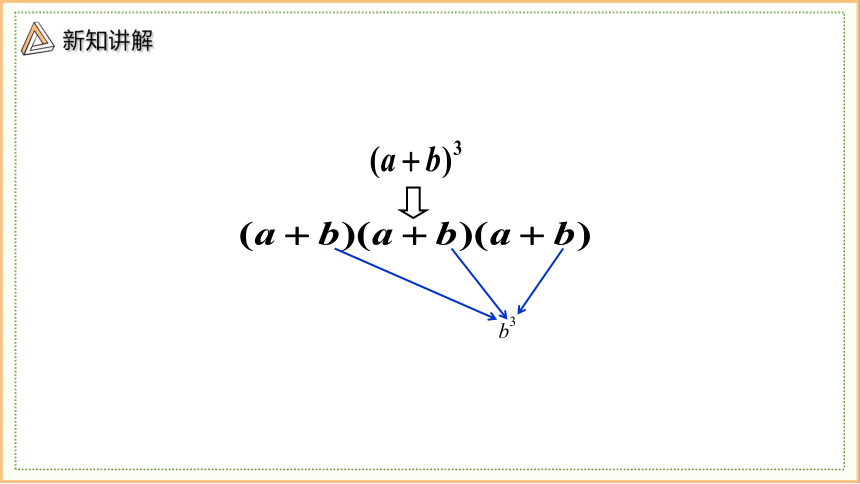
(a+b)3
(a+b)(a+b)(a+b)
a2b
a2b
a2b
ab2
ab2
ab2
b3
a3
a2b
ab2
b3
展开式的每一项都是从
这三个因式中各取一个
字母相乘得到.
发现:
(a+b)3=a3+3ab2+3a2b+b3
(a+b)(a+b)(a+b)
各项是关于a,b的三次单项式
a3
a2b
ab2
b3
(a+b)4= (a+b) (a+b) (a+b) (a+b)=?
(1)(a+b)4展开后各项形式分别是什么?
(2)各项前的系数代表着什么?
a4 a3b a2b2 ab3 b4
各项前的系数 代表着这些项在展开式中出现的次数
问题:
每个都不取b的情况有1种,即C40 ,则a4前的系数为C40
恰有1个取b的情况有C41种,则a3b前的系数为C41
恰有2个取b的情况有C42 种,则a2b2前的系数为C42
恰有3个取b的情况有C43 种,则ab3前的系数为C43
恰有4个取b的情况有C44种,则b4前的系数为C44
则 (a+b)4 =C40 a4 +C41 a3b +C42 a2b2 +C43 ab3 +C44 b4
(3)你能分析说明各项前的系数吗?
a4 a3b a2b2 ab3 b4
(a+b)n=
二项式定理
每个都不取b的情况有1种,即Cn0 ,则an前的系数为Cn0
恰有1个取b的情况有Cn1种,则an-1b前的系数为Cn1
恰有2个取b的情况有Cn2 种,则an-2b2前的系数为Cn2
......
恰有k个取b的情况有Cnk 种,则an-kbk前的系数为Cnk
......
恰有n个取b的情况有Cnn 种,则bn前的系数为Cnn
(a+b)n=+b+...++...+(n∈N*)
右边的多项式叫做(a+b)n的二项展开式
Cnk an-kbk:二项展开式的通项,记作Tk+1;
Cnk : 二项式系数.
①二项展开式共有n+1项
②各项中a的指数从n起依次减小1,到0为止,
各项中b的指数从0起依次增加1,到n为止.
如(1+x)n = Cn0 + Cn1 x+ Cn2 x2+ … +Cnk xk +…+ xn
注意:
二项式定理
(a+b)n=+b+...++...+(n∈N*)
例1
解:
(1)(x+)6=++++++
=x6+6x4+15x2+20+15++
(2)(-)6=()6
例2
求(1+2x)7的展开式的第4项.
求:(1)第4项的二项式系数.
(2)第4项的系数.
解:
(1+2x)7的展开式的第4项是
T3+1=C73 17-3 (2x)3 =35×23×x3 =280x3
第4项的二项式系数是C73 =35
第4项的系数是280
方法归纳
(1)注意对二项式定理的灵活应用;
(2)注意区别二项式系数与项的系数的概念
二项式系数:Cnr;
项的系数:二项式系数与数字系数的积
(3)求二项式系数或项的系数的一种方法是将二项式展开.
例3 (多选)在 的展开式中,下列说法正确的是( )
A.展开式中各项的通项为Tr+1=
B.展开式中各项的系数等于其二项式系数
C.x的幂指数是整数的项共有5项
D.展开式中存在常数项
当r分别取0,6,12,18,24时,x的幂指数为整数,所以x的幂指数有5项是整数项,C正确.
求二项展开式的特定项的常见题型:
①求第k项,Tk=Cnk-1an-k+1bk-1;
②求含xk的项(或 xpyq 的项);
③求常数项;
④求有理项.
方法:根据通项Tk+1=Cnkan-kbk,建立方程求k,再将k的值
代回通项求解,注意k的取值范围(k=0,1,2,…,n).
方法归纳
1. 求(x+a)12的展开式中的倒数第4项.
解:
(1)(x+a)12的展开式有13项,倒数第4项是它的第10项
2. 求(+)9的展开式常数项、中间两项
T9+1==220
(2)Tr+1==
由=0得r=6.
T7==2268
T5=T4+1==42x3
T6=T5+1==42
1)注意二项式定理中二项展开式的特征;
2)区别二项式系数,项的系数;
3)掌握用通项公式求二项式系数,项的系数及项.
易错提醒
本节课你学到了哪些知识?
6.3.1 二项式定理
第 六 章 计 数 原 理
1.能用多项式法则和计数原理推导二项式定理,会用二项式定理
求解二项展开式.
2.理解二项式定理,会利用定理解决与二项式有关的简单问题.
想一想:你还记得什么是二项式吗?
对于a+b,(a+b) ,(a+b) ,(a+b) 等代数式,数学上统称为二项式,其一般形式为:(a+b)n (n∈N*).
在许多代数问题中需要将二项式展开,因此,二项式定理研究的是(a+b)n展开后的表达式的一般结构.那么(a+b)n 的展开式是什么呢
(a+b)2
(a+b)3
那么将(a+b)4 ,(a+b)5 . . .展开后,它们的各项是什么呢?
=C20 a2 + C21 ab+ C22 b2
= C30a3 +C31a2b+C32ab2 +C33 b3
=a3 + 3a2b+3ab2 + b3
= a2 +2ab+b2
我们先来展开下面的式子:
(a+b)2= (a+b) (a+b)
展开后其项的形式为:a2 , ab , b2
这三项的系数为各项在展开式中出现的次数.
考虑b:
每个都不取b的情况有C20 种,则a2前的系数为C20
恰有1个取b的情况有C21种,则ab前的系数为C21
恰有2个取b的情况有C22 种,则b2前的系数为C22
(a+b)2 = a2 +2ab+b2
=C20 a2 + C21 ab+ C22 b2
(a+b)3=a3 + 3a2b+3ab2 + b3
= C30a3 +C31a2b+C32ab2 +C33 b3
对(a+b)2展开式的分析:
a3
以(a+b)3为例体会组合思想
(a+b)3=a3+3ab2+3a2b+b3
(a+b)3
(a+b)(a+b)(a+b)
a2b
a2b
a2b
ab2
ab2
ab2
b3
a3
a2b
ab2
b3
展开式的每一项都是从
这三个因式中各取一个
字母相乘得到.
发现:
(a+b)3=a3+3ab2+3a2b+b3
(a+b)(a+b)(a+b)
各项是关于a,b的三次单项式
a3
a2b
ab2
b3
(a+b)4= (a+b) (a+b) (a+b) (a+b)=?
(1)(a+b)4展开后各项形式分别是什么?
(2)各项前的系数代表着什么?
a4 a3b a2b2 ab3 b4
各项前的系数 代表着这些项在展开式中出现的次数
问题:
每个都不取b的情况有1种,即C40 ,则a4前的系数为C40
恰有1个取b的情况有C41种,则a3b前的系数为C41
恰有2个取b的情况有C42 种,则a2b2前的系数为C42
恰有3个取b的情况有C43 种,则ab3前的系数为C43
恰有4个取b的情况有C44种,则b4前的系数为C44
则 (a+b)4 =C40 a4 +C41 a3b +C42 a2b2 +C43 ab3 +C44 b4
(3)你能分析说明各项前的系数吗?
a4 a3b a2b2 ab3 b4
(a+b)n=
二项式定理
每个都不取b的情况有1种,即Cn0 ,则an前的系数为Cn0
恰有1个取b的情况有Cn1种,则an-1b前的系数为Cn1
恰有2个取b的情况有Cn2 种,则an-2b2前的系数为Cn2
......
恰有k个取b的情况有Cnk 种,则an-kbk前的系数为Cnk
......
恰有n个取b的情况有Cnn 种,则bn前的系数为Cnn
(a+b)n=+b+...++...+(n∈N*)
右边的多项式叫做(a+b)n的二项展开式
Cnk an-kbk:二项展开式的通项,记作Tk+1;
Cnk : 二项式系数.
①二项展开式共有n+1项
②各项中a的指数从n起依次减小1,到0为止,
各项中b的指数从0起依次增加1,到n为止.
如(1+x)n = Cn0 + Cn1 x+ Cn2 x2+ … +Cnk xk +…+ xn
注意:
二项式定理
(a+b)n=+b+...++...+(n∈N*)
例1
解:
(1)(x+)6=++++++
=x6+6x4+15x2+20+15++
(2)(-)6=()6
例2
求(1+2x)7的展开式的第4项.
求:(1)第4项的二项式系数.
(2)第4项的系数.
解:
(1+2x)7的展开式的第4项是
T3+1=C73 17-3 (2x)3 =35×23×x3 =280x3
第4项的二项式系数是C73 =35
第4项的系数是280
方法归纳
(1)注意对二项式定理的灵活应用;
(2)注意区别二项式系数与项的系数的概念
二项式系数:Cnr;
项的系数:二项式系数与数字系数的积
(3)求二项式系数或项的系数的一种方法是将二项式展开.
例3 (多选)在 的展开式中,下列说法正确的是( )
A.展开式中各项的通项为Tr+1=
B.展开式中各项的系数等于其二项式系数
C.x的幂指数是整数的项共有5项
D.展开式中存在常数项
当r分别取0,6,12,18,24时,x的幂指数为整数,所以x的幂指数有5项是整数项,C正确.
求二项展开式的特定项的常见题型:
①求第k项,Tk=Cnk-1an-k+1bk-1;
②求含xk的项(或 xpyq 的项);
③求常数项;
④求有理项.
方法:根据通项Tk+1=Cnkan-kbk,建立方程求k,再将k的值
代回通项求解,注意k的取值范围(k=0,1,2,…,n).
方法归纳
1. 求(x+a)12的展开式中的倒数第4项.
解:
(1)(x+a)12的展开式有13项,倒数第4项是它的第10项
2. 求(+)9的展开式常数项、中间两项
T9+1==220
(2)Tr+1==
由=0得r=6.
T7==2268
T5=T4+1==42x3
T6=T5+1==42
1)注意二项式定理中二项展开式的特征;
2)区别二项式系数,项的系数;
3)掌握用通项公式求二项式系数,项的系数及项.
易错提醒
本节课你学到了哪些知识?
