1.1观察物体(三)(同步练习)-五年级数学下册同步分层作业(人教版)(含解析)
文档属性
| 名称 | 1.1观察物体(三)(同步练习)-五年级数学下册同步分层作业(人教版)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 677.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-21 00:00:00 | ||
图片预览


文档简介
/ 让教学更有效 精品试卷 | 数学学科
1.1观察物体(三)(同步练习)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.小明用一些大小相同的小正方体搭出了一个立体图形,并从不同方向观察画出了下面的三幅图(如图)。小明所搭出的立体图形最少用了( )个小正方体。
从正面看 从上面看 从右面看
A.5 B.6 C.8 D.11
2.
搭的这个几何体,从正面看是( )。
A. B. C. D.
3.从左面看,看到的图形是( )。
A. B. C. D.
4.去掉一个小正方体后,从它的右侧面看不可能是( )。
A. B. C.
5.下面( )是由4块正方体积木搭成的几何体,且从前面看到的图形与下侧的图形一样。
A. B. C. D.
二、填空题
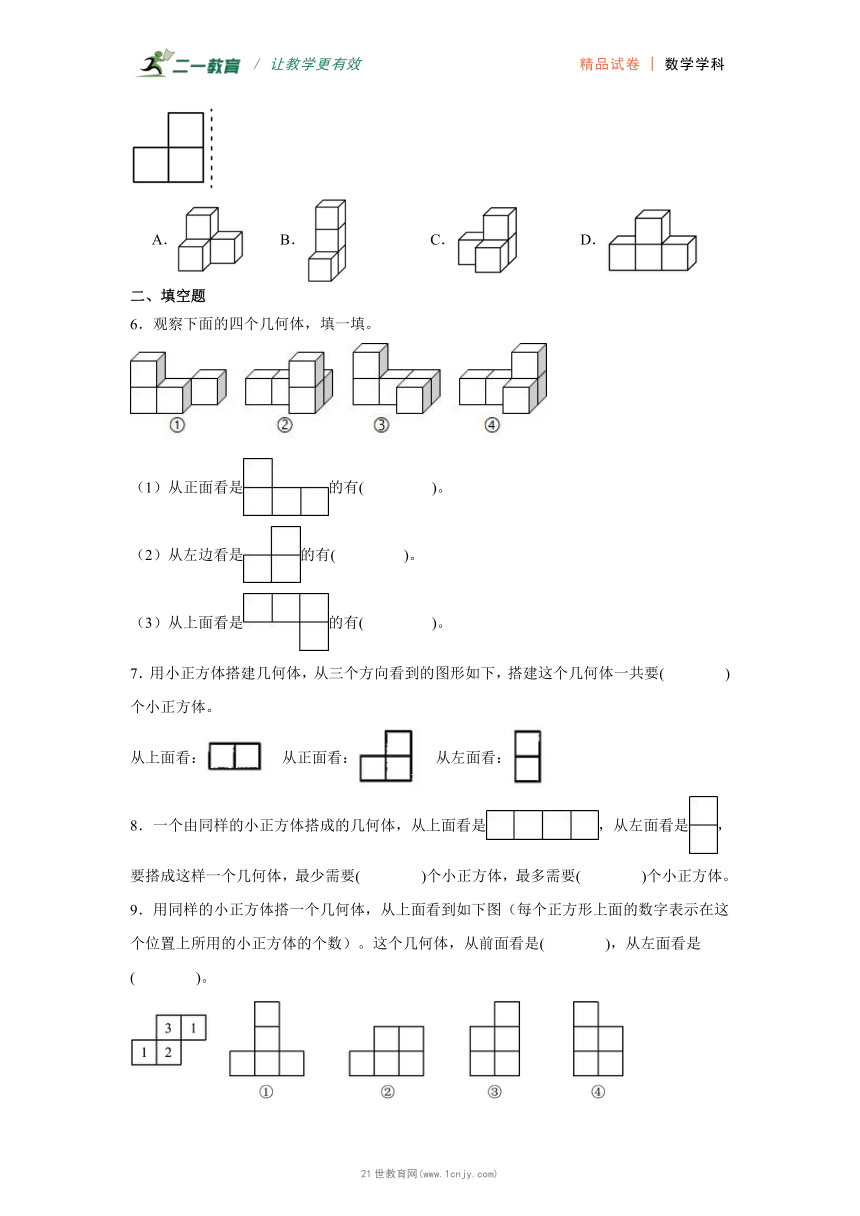
6.观察下面的四个几何体,填一填。
(1)从正面看是的有( )。
(2)从左边看是的有( )。
(3)从上面看是的有( )。
7.用小正方体搭建几何体,从三个方向看到的图形如下,搭建这个几何体一共要( )个小正方体。21·世纪*教育网
从上面看: 从正面看: 从左面看:
8.一个由同样的小正方体搭成的几何体,从上面看是,从左面看是,要搭成这样一个几何体,最少需要( )个小正方体,最多需要( )个小正方体。
9.用同样的小正方体搭一个几何体,从上面看到如下图(每个正方形上面的数字表示在这个位置上所用的小正方体的个数)。这个几何体,从前面看是( ),从左面看是( )。【出处:21教育名师】
10.右图三个图形,分别是从哪个方向看到的?
(1)
从( )面看 从( )面看从( )面看
(2)
从( )面看从( )面看从( )面看
三、判断题
11.从前面、左面看到的形状都相同。( )
12.同一物体的形状从不同角度观察到的形状一定相同。( )
13.从不同的位置观察物体,所看到的形状完全相同。( )
14.根据从正面和上面看到的图形,一定不能确定几何体的具体形状。( )
15.一个几何体,从上面看是,从左面看是,这个几何体是。( )
四、解答题
16.添一个。
(1)从正面看,形状不变,有几种摆法?
(2)从上面看,形状不变,有几种摆法?
(3)从侧面看,形状不变,有几种摆法?
17.一个由正方体组成的立体图形,从不同方向观察分别如下图,那么堆成这个几何体至少需要多少块小正方体?www.21-cn-jy.com
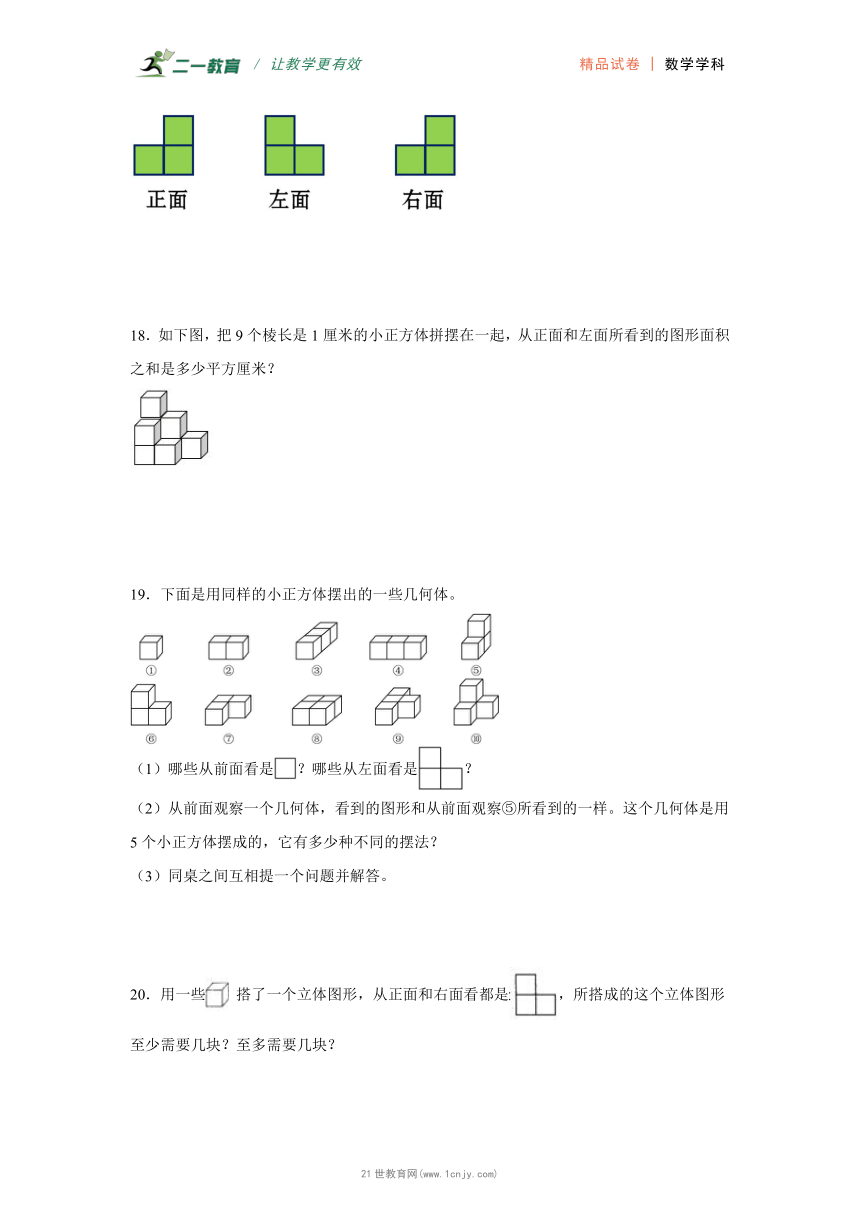
18.如下图,把9个棱长是1厘米的小正方体拼摆在一起,从正面和左面所看到的图形面积之和是多少平方厘米?www-2-1-cnjy-com
19.下面是用同样的小正方体摆出的一些几何体。
(1)哪些从前面看是?哪些从左面看是?
(2)从前面观察一个几何体,看到的图形和从前面观察⑤所看到的一样。这个几何体是用5个小正方体摆成的,它有多少种不同的摆法?21*cnjy*com
(3)同桌之间互相提一个问题并解答。
20.用一些 搭了一个立体图形,从正面和右面看都是,所搭成的这个立体图形至少需要几块?至多需要几块?【来源:21cnj*y.co*m】
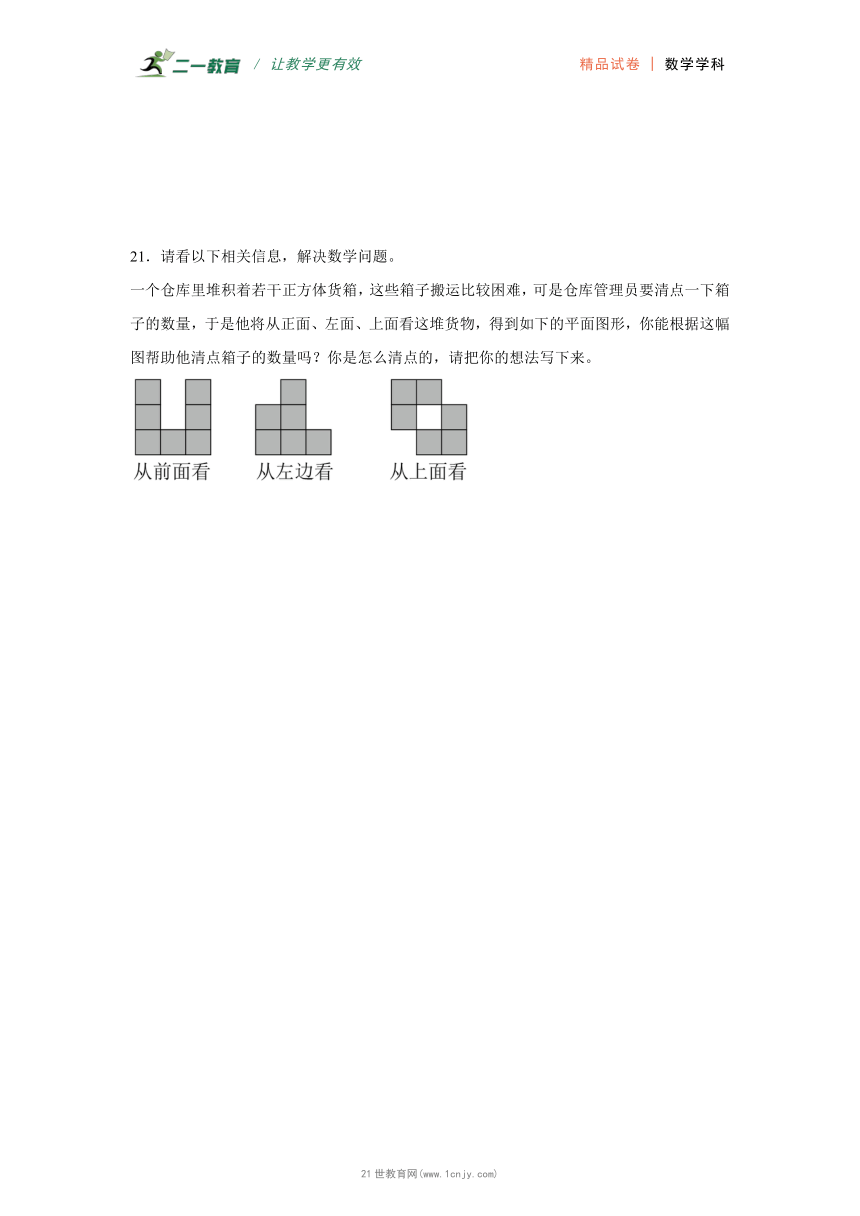
21.请看以下相关信息,解决数学问题。
一个仓库里堆积着若干正方体货箱,这些箱子搬运比较困难,可是仓库管理员要清点一下箱子的数量,于是他将从正面、左面、上面看这堆货物,得到如下的平面图形,你能根据这幅图帮助他清点箱子的数量吗?你是怎么清点的,请把你的想法写下来。
参考答案:
1.B
【分析】通过从不同方向观察到的图形来确定小正方体的最少数量。从正面看可以确定每列小正方体的数量,从上面看可以确定层数和每行的数量,从右面看可以辅助验证。
【详解】从正面看,有三列,左边一列最高是1个,中间一列最高是3个,右边一列最高是 1 个;从上面看,有两行,前面一行有3个,后面一行有 1 个。从右面看,前面一行有3层,后面一行只有1层。综合从正面、上面和右面看到的图形,最少需要6个小正方体,摆放方式为:前面一行左边 1 个,中间3个,右边1个,后面一行中间1个。
即小明所搭出的立体图形最少用了6个小正方体。
故答案为:B
2.A
【解析】由题意可知:从上面看这个几何体的形状是,上面的数字表示所用的几何体的个数,由此可知这个几何体从正面看到的图形有两层,第一层有3个正方形,第二层的中间有一个小正方形即:;据此解答。21教育网
【详解】由分析可知:这个几何体从正面看到的图形有两层,第一层有3个正方形,第二层的中间有一个小正方形即:。2·1·c·n·j·y
故选:A
【点睛】本题考查了从不同的角度观察物体,关键是要认真分析题目,根据从上面看到图形的特点确定立体图形的形状,再根据立体图形的形状,分析从不同角度观察到的图形的特点。
3.A
【分析】由图形可得出:有前后两排,第一排有上下两层,其中上面一层有一个,下面一层有3个;后一排有一个小正方形。从左面看,能看到上下两层,其中第一层有2个正方体,第二层有一个正方体,且第二层正方体在右上方。21*cnjy*com
【详解】从左面看,看到的图形是:。
故答案为:A
【点睛】本题主要考查的是从不同方位看图形,解题的关键是运用空间思维能力得出左视图,进而得出答案。
4.A
【分析】观察图形可知,如图:,若去掉1号正方体,从右面看到的图形是;若去掉3号正方体,从右面看到的图形是;若去掉4号正方体,从右面看到的图形是。据此选择即可。
【详解】由分析可知:
去掉一个小正方体后,从它的右侧面看不可能是。
故答案为:A
【点睛】本题考查观察物体,关键是具有一定的空间想象能力,能想象出从不同角度观察到的形状。
5.C
【分析】根据对三视图的认识分别画出每个选项从前面看到的图形即可。
【详解】A.从前面看到的图形有两层,第一层有2个小正方形,第二层有1个小正方形,靠左齐;
B.从前面看到的图形有三层,每一层都有1个正方形,3个小正方形都对齐;
C.从前面看到的图形有两层,第一层有2个小正方形,第二层有1个小正方形,靠右齐;
D.从前面看到的图形有两层,第一层有3个小正方形,第二层有1个小正方形,靠中间齐。
故答案为:C
【点睛】熟练掌握对三视图的认识是解答此题的关键。
6. ①③ ①② ②③④
【分析】分别从不同的方向观察几何体,判断出观察到的图形有几个正方形以及每个小正方形的位置即可填空。
【详解】①②③④从正面看是依次是:;
①②③④从左边看是依次是:;
①②③④从上面看是依次是:。
故答案是:①③;①②;②③④。
【点睛】做此类题时,应认真审题,充分发挥空间想象力,从不同的方向观察几何体的形状,根据看到的形状即可选择。21·cn·jy·com
7.3
【分析】根据观察题目中的三视图可知,下层2个在一排,上层右侧有1个小正方体,共3个小正方体。
【详解】据分析可知,搭建这个几何体一共要3个小正方体。
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
8. 5/五 8/八
【分析】这个几何体从上面看到的图形是,至少有4个小正方体,结合从左面看到的图形是,说明第二层有1~4个小正方体;如果第二层只有1个小正方体,小正方体最少的摆法:、、、;如果第二层有4个小正方体,小正方体最多的摆法:;据此解答。21教育名师原创作品
【详解】根据分析得,4+1=5(个)
4+4=8(个)
要搭成这样一个几何体,最少需要5个小正方体,最多需要8个小正方体。
【点睛】本题考查从不同的方向观察物体,解答本题的关键是掌握根据物体三视图确定物体形状的方法。
9. ① ④
【分析】结合从上面看到的平面图以及所用小正方体的个数,从前面看有3列,从左往右,分别是1个、3个、1个,下齐;从左面看有2列,从左往右,分别是3个、2个,下齐;据此解答。21世纪教育网版权所有
【详解】这个几何体,从前面看是①,从左面看是④。
10. 正 上 左 上 左 正
【分析】分别从不同的方向观察几何体,判断出观察到的图形有几个正方形以及每个小正方形的位置即可填空。
【详解】(1)从正面看有两层,下面一层三个正方形,中间的上面有一个正方形,如图;
从上面看有两层,上面一层三个正方形,最右端的下面有一个正方形,如图;
从左面看有两层,下面一层两个正方形,左端的上面有一个正方形,如图;
(2)从上面看有两层,上面一层三个正方形,中间的下面有一个正方形,如图;
从左面看有两层,下面一层两个正方形,右端的上面有一个正方形,如图;
从正面看有两层,下面一层三个正方形,中间的上面有一个正方形,如图。
【点睛】做此类题时,应认真审题,充分发挥空间想象力,从不同的方向观察到的几何体的形状,根据看到的形状即可解答。
11.√
【分析】观察图形可知,该立体图形从前面和左面看到的形状都是有两层,第一层有2个小正方形,第二层有1个小正方形,左齐。据此进行判断即可。
【详解】由分析可知:
从前面、左面看到的形状都相同。原题干说法正确。
故答案为:√
【点睛】本题考查观察物体,明确从不同方向观察到的形状是解题的关键。
12.×
【分析】对应一般的物体,从不同的位置观察物体,所看到的形状是不同的;但有特殊情况,如果这个物体是正方体,那么从正面、侧面和上面看到的都是一个正方形,即看到的形状一样;据此判断即可。
【详解】如圆柱,圆锥从不同角度观察到的形状不同,所以同一物体的形状从不同角度观察到的形状一定相同,是错误的。
故答案为:×
【点睛】解答此题的关键:根据题意,找出反例,进行分析,进而得出结论。
13.×
【分析】从不同的位置观察物体,所看到的形状有可能完全相同,也有可能不同,据此判断即可。
【详解】从不同的位置观察物体,所看到的形状可能是不同的。
例如,观察下面的几何体,从正面看,看到的是由两个正方形拼成的长方形,从左面看,看到的是一个正方形。
故答案为:×
【点睛】此题主要考查从不同的位置观察物体,解题的关键是看能否举出例子,证明从不同的位置观察物体,所看到的形状可能是不同的。
14.×
【解析】略
15.×
【分析】根据从不同角度观察立体图形的方法可知:几何体从上面看是,从右面看是;由此进判断即可。
【详解】由分析可知:几何体从上面看是,从右面看是;所以原题说法错误。
故答案为:×
【点睛】本题考查了从不同角度观察物体,关键是要掌握从不同角度观察物体的方法,会根据图形的特点,分析从不同角度看到立体图形的面的特点。【来源:21·世纪·教育·网】
16.(1)8种;
(2)5种;
(3)6种
【分析】(1)从正面看,形状不变,有8种摆法,只要摆在每个正方体的前面或后面即可;
(2)从上面看,形状不变,有5种摆法,只要摆在每个正方体的上面即可;
(3)从侧面看,形状不变,有6种摆法,只要摆在正方体的左边或右边,摆在左边有2种,在右边稍复杂,有4种摆法,因此共6种;据此解答。
【详解】(1)从正面看,形状不变,有8种摆法:
(2)从上面看,形状不变,有5种摆法:
(3)从侧面看,形状不变,有6种摆法:
【点睛】此题考查了从不同方向观察物体和几何体,解答此题关键是要全面考虑。
17.3块
【详解】略
18.11平方厘米
【分析】计算出小正方体每个面的面积是1平方厘米,从正面看到的有6个面,从左面看到的有5个面,加起来11个面,乘每个面的面积即可。21cnjy.com
【详解】1×1×(6+5)=11(平方厘米)
答:从正面和左面所看到的图形面积之和是11平方厘米。
【点睛】此题解题关键是认识物体的三视图,学会观察的方法,考查学生的空间想象力。
19.(1)①③;⑤⑩
(2)有7种摆法。
(3)哪些从左边看是?①②④(答案不唯一)
【分析】
(1)根据观察几何体可知,①③从前面看是,⑤⑩从左面看是。
(2)观察⑤可以看出,从前面看是由两个正方形竖着叠起来的,用5个小正方体来摆,只要把5个小正方体摆成一列两行即可,所以有7种摆法。2-1-c-n-j-y
(3)哪些从左边看是?
【详解】
(1)①③从前面看是,⑤⑩从左面看是。
(2)根据对图形的观察,结合空间想象能力可知有7种摆法。
(3)哪些从左边看是?①②④(答案不唯一)
20.最少需要1+2=3(块)最多需要2+3=5(块)
【详解】略
21.11个;具体想法见详解
【分析】
根据从上面和从左面看到的图形可以知道第一排有1层,中间一排有3层,第三排有2层且中间那一排的中间没有货物;再根据从前面看到的图形知道中间那一排的左侧和右侧有3层,第三排的中间有1层,即(图形上的数字表示从上面看时,这个位置上箱子的个数),把从上面看到的图形上的数字相加即为箱子的总数量,据此解答。
【详解】根据从上面和左面看到的图形可以确定第一排,第二排,第三排的箱子层数分别是:1层,3层和2层并且第二排的中间是没有箱子的;再根据从前面和左边看到的图形可以知道第二排的左侧和右侧各有3层,第三排的中间只有1个箱子,左侧有2个箱子,因此从上面看时每个位置上箱子的个数如下:【版权所有:21教育】
把图形上的数字相加即为箱子的总数量:2+1+3+3+1+1=11(个)
答:一共有11个箱子。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
1.1观察物体(三)(同步练习)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.小明用一些大小相同的小正方体搭出了一个立体图形,并从不同方向观察画出了下面的三幅图(如图)。小明所搭出的立体图形最少用了( )个小正方体。
从正面看 从上面看 从右面看
A.5 B.6 C.8 D.11
2.
搭的这个几何体,从正面看是( )。
A. B. C. D.
3.从左面看,看到的图形是( )。
A. B. C. D.
4.去掉一个小正方体后,从它的右侧面看不可能是( )。
A. B. C.
5.下面( )是由4块正方体积木搭成的几何体,且从前面看到的图形与下侧的图形一样。
A. B. C. D.
二、填空题
6.观察下面的四个几何体,填一填。
(1)从正面看是的有( )。
(2)从左边看是的有( )。
(3)从上面看是的有( )。
7.用小正方体搭建几何体,从三个方向看到的图形如下,搭建这个几何体一共要( )个小正方体。21·世纪*教育网
从上面看: 从正面看: 从左面看:
8.一个由同样的小正方体搭成的几何体,从上面看是,从左面看是,要搭成这样一个几何体,最少需要( )个小正方体,最多需要( )个小正方体。
9.用同样的小正方体搭一个几何体,从上面看到如下图(每个正方形上面的数字表示在这个位置上所用的小正方体的个数)。这个几何体,从前面看是( ),从左面看是( )。【出处:21教育名师】
10.右图三个图形,分别是从哪个方向看到的?
(1)
从( )面看 从( )面看从( )面看
(2)
从( )面看从( )面看从( )面看
三、判断题
11.从前面、左面看到的形状都相同。( )
12.同一物体的形状从不同角度观察到的形状一定相同。( )
13.从不同的位置观察物体,所看到的形状完全相同。( )
14.根据从正面和上面看到的图形,一定不能确定几何体的具体形状。( )
15.一个几何体,从上面看是,从左面看是,这个几何体是。( )
四、解答题
16.添一个。
(1)从正面看,形状不变,有几种摆法?
(2)从上面看,形状不变,有几种摆法?
(3)从侧面看,形状不变,有几种摆法?
17.一个由正方体组成的立体图形,从不同方向观察分别如下图,那么堆成这个几何体至少需要多少块小正方体?www.21-cn-jy.com
18.如下图,把9个棱长是1厘米的小正方体拼摆在一起,从正面和左面所看到的图形面积之和是多少平方厘米?www-2-1-cnjy-com
19.下面是用同样的小正方体摆出的一些几何体。
(1)哪些从前面看是?哪些从左面看是?
(2)从前面观察一个几何体,看到的图形和从前面观察⑤所看到的一样。这个几何体是用5个小正方体摆成的,它有多少种不同的摆法?21*cnjy*com
(3)同桌之间互相提一个问题并解答。
20.用一些 搭了一个立体图形,从正面和右面看都是,所搭成的这个立体图形至少需要几块?至多需要几块?【来源:21cnj*y.co*m】
21.请看以下相关信息,解决数学问题。
一个仓库里堆积着若干正方体货箱,这些箱子搬运比较困难,可是仓库管理员要清点一下箱子的数量,于是他将从正面、左面、上面看这堆货物,得到如下的平面图形,你能根据这幅图帮助他清点箱子的数量吗?你是怎么清点的,请把你的想法写下来。
参考答案:
1.B
【分析】通过从不同方向观察到的图形来确定小正方体的最少数量。从正面看可以确定每列小正方体的数量,从上面看可以确定层数和每行的数量,从右面看可以辅助验证。
【详解】从正面看,有三列,左边一列最高是1个,中间一列最高是3个,右边一列最高是 1 个;从上面看,有两行,前面一行有3个,后面一行有 1 个。从右面看,前面一行有3层,后面一行只有1层。综合从正面、上面和右面看到的图形,最少需要6个小正方体,摆放方式为:前面一行左边 1 个,中间3个,右边1个,后面一行中间1个。
即小明所搭出的立体图形最少用了6个小正方体。
故答案为:B
2.A
【解析】由题意可知:从上面看这个几何体的形状是,上面的数字表示所用的几何体的个数,由此可知这个几何体从正面看到的图形有两层,第一层有3个正方形,第二层的中间有一个小正方形即:;据此解答。21教育网
【详解】由分析可知:这个几何体从正面看到的图形有两层,第一层有3个正方形,第二层的中间有一个小正方形即:。2·1·c·n·j·y
故选:A
【点睛】本题考查了从不同的角度观察物体,关键是要认真分析题目,根据从上面看到图形的特点确定立体图形的形状,再根据立体图形的形状,分析从不同角度观察到的图形的特点。
3.A
【分析】由图形可得出:有前后两排,第一排有上下两层,其中上面一层有一个,下面一层有3个;后一排有一个小正方形。从左面看,能看到上下两层,其中第一层有2个正方体,第二层有一个正方体,且第二层正方体在右上方。21*cnjy*com
【详解】从左面看,看到的图形是:。
故答案为:A
【点睛】本题主要考查的是从不同方位看图形,解题的关键是运用空间思维能力得出左视图,进而得出答案。
4.A
【分析】观察图形可知,如图:,若去掉1号正方体,从右面看到的图形是;若去掉3号正方体,从右面看到的图形是;若去掉4号正方体,从右面看到的图形是。据此选择即可。
【详解】由分析可知:
去掉一个小正方体后,从它的右侧面看不可能是。
故答案为:A
【点睛】本题考查观察物体,关键是具有一定的空间想象能力,能想象出从不同角度观察到的形状。
5.C
【分析】根据对三视图的认识分别画出每个选项从前面看到的图形即可。
【详解】A.从前面看到的图形有两层,第一层有2个小正方形,第二层有1个小正方形,靠左齐;
B.从前面看到的图形有三层,每一层都有1个正方形,3个小正方形都对齐;
C.从前面看到的图形有两层,第一层有2个小正方形,第二层有1个小正方形,靠右齐;
D.从前面看到的图形有两层,第一层有3个小正方形,第二层有1个小正方形,靠中间齐。
故答案为:C
【点睛】熟练掌握对三视图的认识是解答此题的关键。
6. ①③ ①② ②③④
【分析】分别从不同的方向观察几何体,判断出观察到的图形有几个正方形以及每个小正方形的位置即可填空。
【详解】①②③④从正面看是依次是:;
①②③④从左边看是依次是:;
①②③④从上面看是依次是:。
故答案是:①③;①②;②③④。
【点睛】做此类题时,应认真审题,充分发挥空间想象力,从不同的方向观察几何体的形状,根据看到的形状即可选择。21·cn·jy·com
7.3
【分析】根据观察题目中的三视图可知,下层2个在一排,上层右侧有1个小正方体,共3个小正方体。
【详解】据分析可知,搭建这个几何体一共要3个小正方体。
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
8. 5/五 8/八
【分析】这个几何体从上面看到的图形是,至少有4个小正方体,结合从左面看到的图形是,说明第二层有1~4个小正方体;如果第二层只有1个小正方体,小正方体最少的摆法:、、、;如果第二层有4个小正方体,小正方体最多的摆法:;据此解答。21教育名师原创作品
【详解】根据分析得,4+1=5(个)
4+4=8(个)
要搭成这样一个几何体,最少需要5个小正方体,最多需要8个小正方体。
【点睛】本题考查从不同的方向观察物体,解答本题的关键是掌握根据物体三视图确定物体形状的方法。
9. ① ④
【分析】结合从上面看到的平面图以及所用小正方体的个数,从前面看有3列,从左往右,分别是1个、3个、1个,下齐;从左面看有2列,从左往右,分别是3个、2个,下齐;据此解答。21世纪教育网版权所有
【详解】这个几何体,从前面看是①,从左面看是④。
10. 正 上 左 上 左 正
【分析】分别从不同的方向观察几何体,判断出观察到的图形有几个正方形以及每个小正方形的位置即可填空。
【详解】(1)从正面看有两层,下面一层三个正方形,中间的上面有一个正方形,如图;
从上面看有两层,上面一层三个正方形,最右端的下面有一个正方形,如图;
从左面看有两层,下面一层两个正方形,左端的上面有一个正方形,如图;
(2)从上面看有两层,上面一层三个正方形,中间的下面有一个正方形,如图;
从左面看有两层,下面一层两个正方形,右端的上面有一个正方形,如图;
从正面看有两层,下面一层三个正方形,中间的上面有一个正方形,如图。
【点睛】做此类题时,应认真审题,充分发挥空间想象力,从不同的方向观察到的几何体的形状,根据看到的形状即可解答。
11.√
【分析】观察图形可知,该立体图形从前面和左面看到的形状都是有两层,第一层有2个小正方形,第二层有1个小正方形,左齐。据此进行判断即可。
【详解】由分析可知:
从前面、左面看到的形状都相同。原题干说法正确。
故答案为:√
【点睛】本题考查观察物体,明确从不同方向观察到的形状是解题的关键。
12.×
【分析】对应一般的物体,从不同的位置观察物体,所看到的形状是不同的;但有特殊情况,如果这个物体是正方体,那么从正面、侧面和上面看到的都是一个正方形,即看到的形状一样;据此判断即可。
【详解】如圆柱,圆锥从不同角度观察到的形状不同,所以同一物体的形状从不同角度观察到的形状一定相同,是错误的。
故答案为:×
【点睛】解答此题的关键:根据题意,找出反例,进行分析,进而得出结论。
13.×
【分析】从不同的位置观察物体,所看到的形状有可能完全相同,也有可能不同,据此判断即可。
【详解】从不同的位置观察物体,所看到的形状可能是不同的。
例如,观察下面的几何体,从正面看,看到的是由两个正方形拼成的长方形,从左面看,看到的是一个正方形。
故答案为:×
【点睛】此题主要考查从不同的位置观察物体,解题的关键是看能否举出例子,证明从不同的位置观察物体,所看到的形状可能是不同的。
14.×
【解析】略
15.×
【分析】根据从不同角度观察立体图形的方法可知:几何体从上面看是,从右面看是;由此进判断即可。
【详解】由分析可知:几何体从上面看是,从右面看是;所以原题说法错误。
故答案为:×
【点睛】本题考查了从不同角度观察物体,关键是要掌握从不同角度观察物体的方法,会根据图形的特点,分析从不同角度看到立体图形的面的特点。【来源:21·世纪·教育·网】
16.(1)8种;
(2)5种;
(3)6种
【分析】(1)从正面看,形状不变,有8种摆法,只要摆在每个正方体的前面或后面即可;
(2)从上面看,形状不变,有5种摆法,只要摆在每个正方体的上面即可;
(3)从侧面看,形状不变,有6种摆法,只要摆在正方体的左边或右边,摆在左边有2种,在右边稍复杂,有4种摆法,因此共6种;据此解答。
【详解】(1)从正面看,形状不变,有8种摆法:
(2)从上面看,形状不变,有5种摆法:
(3)从侧面看,形状不变,有6种摆法:
【点睛】此题考查了从不同方向观察物体和几何体,解答此题关键是要全面考虑。
17.3块
【详解】略
18.11平方厘米
【分析】计算出小正方体每个面的面积是1平方厘米,从正面看到的有6个面,从左面看到的有5个面,加起来11个面,乘每个面的面积即可。21cnjy.com
【详解】1×1×(6+5)=11(平方厘米)
答:从正面和左面所看到的图形面积之和是11平方厘米。
【点睛】此题解题关键是认识物体的三视图,学会观察的方法,考查学生的空间想象力。
19.(1)①③;⑤⑩
(2)有7种摆法。
(3)哪些从左边看是?①②④(答案不唯一)
【分析】
(1)根据观察几何体可知,①③从前面看是,⑤⑩从左面看是。
(2)观察⑤可以看出,从前面看是由两个正方形竖着叠起来的,用5个小正方体来摆,只要把5个小正方体摆成一列两行即可,所以有7种摆法。2-1-c-n-j-y
(3)哪些从左边看是?
【详解】
(1)①③从前面看是,⑤⑩从左面看是。
(2)根据对图形的观察,结合空间想象能力可知有7种摆法。
(3)哪些从左边看是?①②④(答案不唯一)
20.最少需要1+2=3(块)最多需要2+3=5(块)
【详解】略
21.11个;具体想法见详解
【分析】
根据从上面和从左面看到的图形可以知道第一排有1层,中间一排有3层,第三排有2层且中间那一排的中间没有货物;再根据从前面看到的图形知道中间那一排的左侧和右侧有3层,第三排的中间有1层,即(图形上的数字表示从上面看时,这个位置上箱子的个数),把从上面看到的图形上的数字相加即为箱子的总数量,据此解答。
【详解】根据从上面和左面看到的图形可以确定第一排,第二排,第三排的箱子层数分别是:1层,3层和2层并且第二排的中间是没有箱子的;再根据从前面和左边看到的图形可以知道第二排的左侧和右侧各有3层,第三排的中间只有1个箱子,左侧有2个箱子,因此从上面看时每个位置上箱子的个数如下:【版权所有:21教育】
把图形上的数字相加即为箱子的总数量:2+1+3+3+1+1=11(个)
答:一共有11个箱子。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
