2016年宁波市中考复习会议资料.pptx
文档属性
| 名称 | 2016年宁波市中考复习会议资料.pptx |

|
|
| 格式 | zip | ||
| 文件大小 | 11.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-24 13:00:26 | ||
图片预览




文档简介
课件27张PPT。“一生万物”练思维“万物归一”悟本质鄞州外国语中学 姚静我们工作室致力于专业PPT模板的发布,课件及汇报PPT的美化,并为您提供专业的PPT个性定制服务。专业的团队,完善的售后,热情的服务复习课教学模式和方法的选择是提高复习效率的关键,因此我们提升复习教学效率的主阵地在课堂.一题多解一题多变多解归一多题归一练思维悟本质一题多解单击此处添加标题“一题多解”,就是同一个题目,尽可能考虑多种不同的解法.它能培养学生综合运用数学知识的能力,复习过程中充分发挥例题的教学功能,尽量从多方面多角度去思考问题,可以达到以少胜多的目的.单击此处添加标题 从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5 km,下坡的速度比在平路上的速度每小时多5 km.设小明出发x h 后,到达离甲地y km的地方,图中的折线O—A—B—C—D—E 表示y 与x 之间的函数关系. 如果小明两次经过途中某一地点的时间间隔为0.15 h,那么该地点离甲地多远?一题多解 根据两次经过途中某一地点的题意,
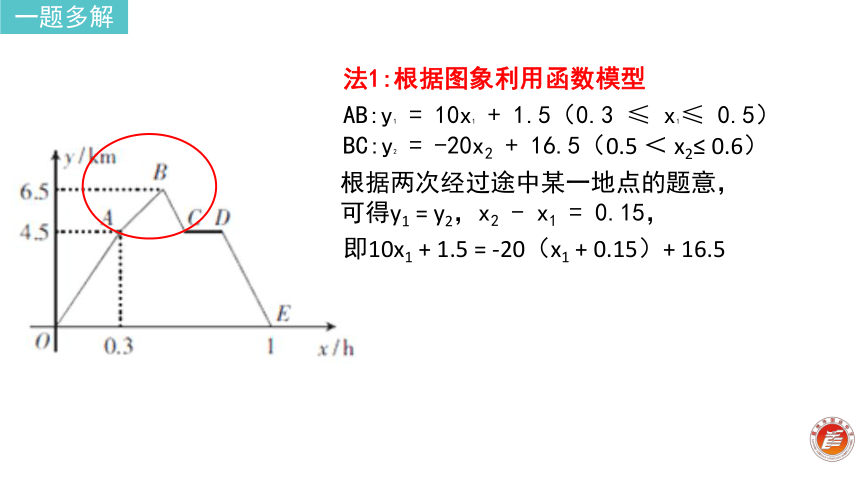
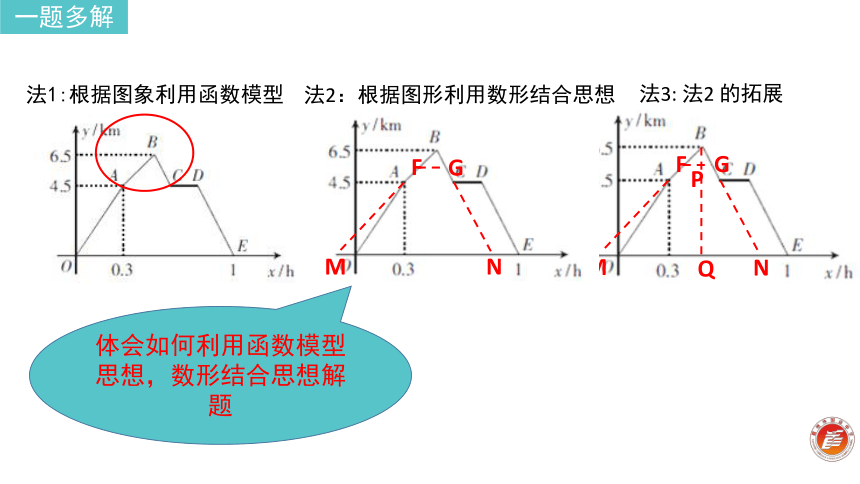
可得y1 = y2,x2 - x1 = 0.15,法1:根据图象利用函数模型AB:y1 = 10x1 + 1.5(0.3 ≤ x1≤ 0.5)即10x1 + 1.5 = -20(x1 + 0.15)+ 16.5一题多解BC:y2 = -20x2 + 16.5(0.5 < x2≤ 0.6) 设点F的纵坐标为y法2:根据图形利用数形结合思想由已知,得FG=0.15
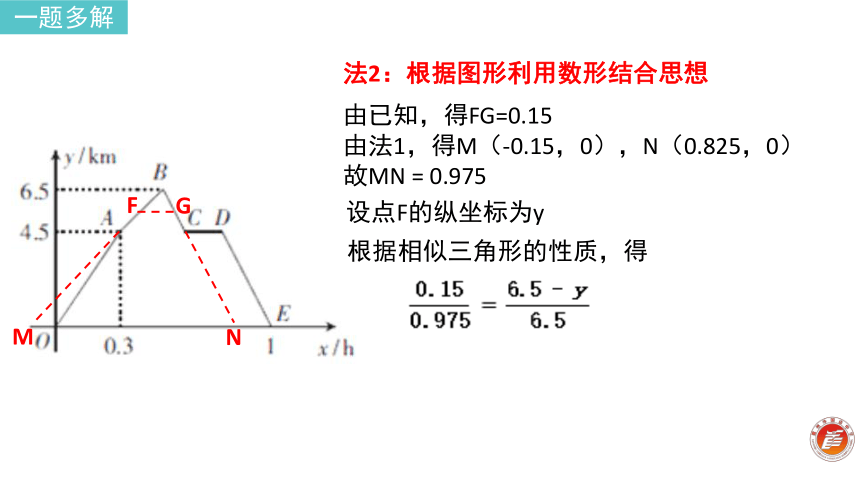
由法1,得M(-0.15,0),N(0.825,0)
故MN = 0.975根据相似三角形的性质,得 MNFG一题多解 而FG = 0.15,所以PF = 0.1
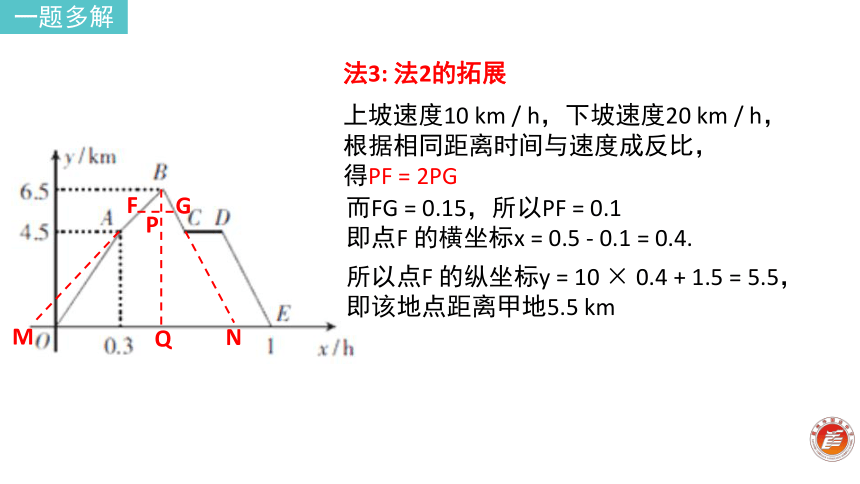
即点F 的横坐标x = 0.5 - 0.1 = 0.4.法3: 法2的拓展上坡速度10 km / h,下坡速度20 km / h,
根据相同距离时间与速度成反比,
得PF = 2PG所以点F 的纵坐标y = 10 × 0.4 + 1.5 = 5.5,
即该地点距离甲地5.5 kmMNFGQP一题多解 法3: 法2 的拓展法1:根据图象利用函数模型法2:根据图形利用数形结合思想体会如何利用函数模型思想,数形结合思想解题一题多解一题多变单击此处添加标题“一题多变”,可指两方面的情况:一方面是条件不变,还可以推出哪些结论?这些结论之间有什么联系?另一方面,改变题型,能推出怎样的新结论.在复习课的教学中适当地一题多变,沟通知识之间的联系, 指给学生考虑问题的方法,提高学生分析与演绎能力, 训练学生积极思维,触类旁通从而提高学生思维敏捷性、灵活性和深刻性,以及勇于探索知识的能力.单击此处添加标题原题:已知,如图1,正方形ABCD的对角线AC ,BD相交于点O,正方形A'B'C'D'的顶点与点0重合,A'B'交BC于点E , A'D'交CD于点F.
求证:OE=OF方式一:已知不变,直接挖掘其它结论变式1: BE与CF相等吗?请说明理由变式2:求证:∠OEC=∠OFD
(请用不同的方法进行证明)变式3:连接EF,判断△OEF的形状,并说明理由一题多变单击此处添加标题方式二:改变题型变式4:已知,如图2,正方形ABCD对角线相交于点O,正方形A'B'C'D'的顶点与点0重合,A'B'交BC于点E,A'D'交CD于点F,连接EF,若正方形ABCD的边长为12.(1)若EF= ,则FC=________
(2)若FC=x,则△EOF的面积S与x之间的关系是什么?一题多变单击此处添加标题方式二:改变题型变式5:已知,如图3,正方形ABCD对角线相交于点0,正方形A'B'C'D'的顶点与点0重合,A'B'交BC于点E,A'D'交CD于点F,OC'交BC于点G,连接FG若正方形ABCD的边长为12,FG=5,则FC=_______变式4、5都是在原题型的基础上,对原题型结论的进一步延伸探究,是原题结论的进一步拓宽,它利用原图形的特点直角,通过勾股定理构造一元二次方程,建立二次函数模型,体现方程建模和数形结合的数学思想一题多变单击此处添加标题 变式6:正方形ABCD对角线相交于点0,正方形A‘B’C‘D’的顶点与点0重合,正方形绕点0转动,A‘B’交BC于点E,A‘D’交CD于点F.方式二:改变题型(1)若点E为BC的中点,如图4,则点F也为CD的中点吗?证明你的结论.
(2)若点E为BC的三等分点,即EC= BC,如图5,则点F也是CD的三等分点吗?证明你的结论(3)由(1)(2)你得到什么结论?通过类比原题型的基本的三角形全等,得出相应线段之间的关系,体现研究数学常用的由特殊到一般的数学思想.一题多变单击此处添加标题 现在的考试主要是考查学生的四基和四能,体现数学是解决生活中问题的工具学科,在教学中我们要充分挖掘典型内容的潜在智能,恰当地对它进行改变、引伸、拓广、挖掘,实现一题多变,充分发挥其典型习题的作用,使学生对所变习题既有熟悉感又有新鲜感,这样不但能诱发学生的解题欲望,激发求知欲,还能起到以一当十,锻炼学生数学思维的效果,从而有效提高课堂教学效率.一题多变多解归一单击此处添加标题“一题多解”是很多教师在解题教学过程中经常开展的教学活动,然而重视引导学生跟进思考,为什么这道数学题有这么多的解法,却常常因师而异,缺少最后反思、提炼、升华的“临门一脚”,往往会造成学生“入宝山而空返”. 法3: 法2 的拓展法1:根据图象利用函数模型法2:根据图形利用数形结合思想实质都是利用数学思想方法把求点的坐标问题转化为求方程解的问题一题多解单击此处添加标题 已知抛物线y=x2+6x+5的顶点为P,直线l: y=x-1. 抛物线与x轴交于A,B两点,与y轴交于点C,与直线l的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图1),求点M的坐标.(-3,-4)(-2,-3)EF(-5,0)G∵∠APF=90°-∠PAF=90°-(∠PAQ+45°)
=45°-∠PAQ,
又∠ACM=∠PAQ
∴∠A PF=∠MCE∴Rt△CME∽Rt△PAF ∴设M ( x , x2+6x+5),得法1:从“形”的角度,通过构造相似三角形突破问题多解归一(0,5)单击此处添加标题破解本题的核心问题:求解直线CM的解析式(-3,-4)(-2,-3)(-5,0)N在Rt△APQ中,有tan∠PAQ= ∵∠ACM=∠PAQ ∴在Rt△CGN中tan∠NCG =
设GN=n.则GC=3n法2:(0,5)主要障碍是解读 “∠ACM=∠PAQ”的价值.G∵Rt△AGN中,AG=GN=n∴AG+GC=4n=得点N坐标,这样直线CM的解析式
可由C、N两点坐标求得,……多解归一破解本题的关键:求出该直线上除点C外任意一点的坐标单击此处添加标题当∠PAB=∠ANM时,直线AP的解析式:y=-2x -10 可设直线CM的解析式为y=2x+n反思:由“法1”提及的△AQG是等腰直角三角形,可以知道∠BAQ=45°,而∠CAO=45°,再结合∠ACM=∠PAQ,可得∠ACM+∠CAB=∠PAQ+∠BAQ,即∠PAB=∠CNO,所以∠PAB=∠ANMN直线AP、CM的解析式中的k互为相反数多解归一单击此处添加标题 一题多解有利于开阔学生解决问题的视野,发展学生的数学思维;然而在解决一题多解之后,如能进一步反思一道题为何能多解,这些不同思路背后存在着怎样的共同点,多解归一背后的深层结构是什么,多坚持这样的训练,定会让解题教学走上一个新的台阶.特别是对于那些学有余力的学生,如上面的题,在给出两种思路之后,若能帮助学生提炼出最后的深层结构,那么学生对不同的解法会有更为深刻的认识和理解.多解归一多题归一单击此处添加标题“多题归一”, 是将习题分类, 同一类型的题有共同的解题技巧和方法, 也就是说, 同一类型题虽然从表面上看, 提法、条件结论都不同, 但其解法思路和主要步骤大致相同, 我们把这样一类题归并在一起讲解和组织学生练习,达到提高学生综合与归纳能力, 并使知识系统化.单击此处添加标题一、训练体悟(先独立思考完成,再小组交流;其中打*题选做)
1.数轴上到原点的距离为2的点所表示的数是________
2.若 是一个完全平方式,那么m的值是_________
3.函数 与x轴只有一个交点,则a的值是_______
4.已知等腰三角形的一条边长为6,另一条边长为4,则该等腰三角形的周长等于_______
*5.在半径为1的⊙O中,弦AB= ,AC= ,则∠BAC的度数是_______中考复习《分类讨论》的设计二、方法揭示(先独立思考并作简单记录,后小组交流呈现)
在交流完成上述题目并解决后,请你思考下列问题:
1.上述问题中,引起问题的不同结果的原因各是什么?
2.在已学的初中知识范围内,你还碰到过哪些类似的问题?
3.解决这类问题的数学思想方法是什么?应用它解决问题需用注意什么问题?多题归一从有限的问题解决中体会方法的应用,再联系已学的知识范围内的相同类型,寻找问题和方法的共同特征,揭示出分类讨论数学思想方法的本质内涵单击此处添加标题 从案例中可总结多题归一有如下四个步骤:
1.发现多题之间的共同特征,并作出描述;
2.关注差别,研究这类问题大致有几种类型;
3.深入讨论这类问题的本质,形成可操作的解题模块;
4.反思这类题所蕴涵的数学思想方法.
从形式上看,多题归一可以借助图、表、框图等.在实践中,注重师生的共同参与.多题归一单击此处添加标题 任何一个创造过程,都是发散思维和聚合思维的完美结合。而多解、多题归一的训练,则是培养聚合性思维的重要途径。很多数学题,虽然题型各异,研究对象不同,但问题的实质相同,若能对这些“型异质同”或“型近质同”的问题归类分析,抓住共同的本质特征,掌握解答此类问题的规律,就能达到举一反三、事半功倍的教学效果,从而摆脱“题海”泛舟的苦恼。多题归一“一生万物,万物归一” 初三复习不是在同一水平上的简单重复,要创造性地将知识、能力和思想方法在更多的新情境、更高的层次中不断地、反复地渗透,才能达到螺旋式的再认识,再深化乃至升华的结果. 在复习过程中,课堂教学是充满灵感,充满激情,充满理想的过程,不能仅仅停留在习题本身所传达的文字信息上,应重视对已有题型的挖掘、延伸,使学生加深对原题解法的理解,提高学生解题的灵活性,更应注重激发兴趣和求知欲,注重意识、思想和认识方法的渗透和能力的培养.敬请大家
批评指正谢谢!
可得y1 = y2,x2 - x1 = 0.15,法1:根据图象利用函数模型AB:y1 = 10x1 + 1.5(0.3 ≤ x1≤ 0.5)即10x1 + 1.5 = -20(x1 + 0.15)+ 16.5一题多解BC:y2 = -20x2 + 16.5(0.5 < x2≤ 0.6) 设点F的纵坐标为y法2:根据图形利用数形结合思想由已知,得FG=0.15
由法1,得M(-0.15,0),N(0.825,0)
故MN = 0.975根据相似三角形的性质,得 MNFG一题多解 而FG = 0.15,所以PF = 0.1
即点F 的横坐标x = 0.5 - 0.1 = 0.4.法3: 法2的拓展上坡速度10 km / h,下坡速度20 km / h,
根据相同距离时间与速度成反比,
得PF = 2PG所以点F 的纵坐标y = 10 × 0.4 + 1.5 = 5.5,
即该地点距离甲地5.5 kmMNFGQP一题多解 法3: 法2 的拓展法1:根据图象利用函数模型法2:根据图形利用数形结合思想体会如何利用函数模型思想,数形结合思想解题一题多解一题多变单击此处添加标题“一题多变”,可指两方面的情况:一方面是条件不变,还可以推出哪些结论?这些结论之间有什么联系?另一方面,改变题型,能推出怎样的新结论.在复习课的教学中适当地一题多变,沟通知识之间的联系, 指给学生考虑问题的方法,提高学生分析与演绎能力, 训练学生积极思维,触类旁通从而提高学生思维敏捷性、灵活性和深刻性,以及勇于探索知识的能力.单击此处添加标题原题:已知,如图1,正方形ABCD的对角线AC ,BD相交于点O,正方形A'B'C'D'的顶点与点0重合,A'B'交BC于点E , A'D'交CD于点F.
求证:OE=OF方式一:已知不变,直接挖掘其它结论变式1: BE与CF相等吗?请说明理由变式2:求证:∠OEC=∠OFD
(请用不同的方法进行证明)变式3:连接EF,判断△OEF的形状,并说明理由一题多变单击此处添加标题方式二:改变题型变式4:已知,如图2,正方形ABCD对角线相交于点O,正方形A'B'C'D'的顶点与点0重合,A'B'交BC于点E,A'D'交CD于点F,连接EF,若正方形ABCD的边长为12.(1)若EF= ,则FC=________
(2)若FC=x,则△EOF的面积S与x之间的关系是什么?一题多变单击此处添加标题方式二:改变题型变式5:已知,如图3,正方形ABCD对角线相交于点0,正方形A'B'C'D'的顶点与点0重合,A'B'交BC于点E,A'D'交CD于点F,OC'交BC于点G,连接FG若正方形ABCD的边长为12,FG=5,则FC=_______变式4、5都是在原题型的基础上,对原题型结论的进一步延伸探究,是原题结论的进一步拓宽,它利用原图形的特点直角,通过勾股定理构造一元二次方程,建立二次函数模型,体现方程建模和数形结合的数学思想一题多变单击此处添加标题 变式6:正方形ABCD对角线相交于点0,正方形A‘B’C‘D’的顶点与点0重合,正方形绕点0转动,A‘B’交BC于点E,A‘D’交CD于点F.方式二:改变题型(1)若点E为BC的中点,如图4,则点F也为CD的中点吗?证明你的结论.
(2)若点E为BC的三等分点,即EC= BC,如图5,则点F也是CD的三等分点吗?证明你的结论(3)由(1)(2)你得到什么结论?通过类比原题型的基本的三角形全等,得出相应线段之间的关系,体现研究数学常用的由特殊到一般的数学思想.一题多变单击此处添加标题 现在的考试主要是考查学生的四基和四能,体现数学是解决生活中问题的工具学科,在教学中我们要充分挖掘典型内容的潜在智能,恰当地对它进行改变、引伸、拓广、挖掘,实现一题多变,充分发挥其典型习题的作用,使学生对所变习题既有熟悉感又有新鲜感,这样不但能诱发学生的解题欲望,激发求知欲,还能起到以一当十,锻炼学生数学思维的效果,从而有效提高课堂教学效率.一题多变多解归一单击此处添加标题“一题多解”是很多教师在解题教学过程中经常开展的教学活动,然而重视引导学生跟进思考,为什么这道数学题有这么多的解法,却常常因师而异,缺少最后反思、提炼、升华的“临门一脚”,往往会造成学生“入宝山而空返”. 法3: 法2 的拓展法1:根据图象利用函数模型法2:根据图形利用数形结合思想实质都是利用数学思想方法把求点的坐标问题转化为求方程解的问题一题多解单击此处添加标题 已知抛物线y=x2+6x+5的顶点为P,直线l: y=x-1. 抛物线与x轴交于A,B两点,与y轴交于点C,与直线l的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图1),求点M的坐标.(-3,-4)(-2,-3)EF(-5,0)G∵∠APF=90°-∠PAF=90°-(∠PAQ+45°)
=45°-∠PAQ,
又∠ACM=∠PAQ
∴∠A PF=∠MCE∴Rt△CME∽Rt△PAF ∴设M ( x , x2+6x+5),得法1:从“形”的角度,通过构造相似三角形突破问题多解归一(0,5)单击此处添加标题破解本题的核心问题:求解直线CM的解析式(-3,-4)(-2,-3)(-5,0)N在Rt△APQ中,有tan∠PAQ= ∵∠ACM=∠PAQ ∴在Rt△CGN中tan∠NCG =
设GN=n.则GC=3n法2:(0,5)主要障碍是解读 “∠ACM=∠PAQ”的价值.G∵Rt△AGN中,AG=GN=n∴AG+GC=4n=得点N坐标,这样直线CM的解析式
可由C、N两点坐标求得,……多解归一破解本题的关键:求出该直线上除点C外任意一点的坐标单击此处添加标题当∠PAB=∠ANM时,直线AP的解析式:y=-2x -10 可设直线CM的解析式为y=2x+n反思:由“法1”提及的△AQG是等腰直角三角形,可以知道∠BAQ=45°,而∠CAO=45°,再结合∠ACM=∠PAQ,可得∠ACM+∠CAB=∠PAQ+∠BAQ,即∠PAB=∠CNO,所以∠PAB=∠ANMN直线AP、CM的解析式中的k互为相反数多解归一单击此处添加标题 一题多解有利于开阔学生解决问题的视野,发展学生的数学思维;然而在解决一题多解之后,如能进一步反思一道题为何能多解,这些不同思路背后存在着怎样的共同点,多解归一背后的深层结构是什么,多坚持这样的训练,定会让解题教学走上一个新的台阶.特别是对于那些学有余力的学生,如上面的题,在给出两种思路之后,若能帮助学生提炼出最后的深层结构,那么学生对不同的解法会有更为深刻的认识和理解.多解归一多题归一单击此处添加标题“多题归一”, 是将习题分类, 同一类型的题有共同的解题技巧和方法, 也就是说, 同一类型题虽然从表面上看, 提法、条件结论都不同, 但其解法思路和主要步骤大致相同, 我们把这样一类题归并在一起讲解和组织学生练习,达到提高学生综合与归纳能力, 并使知识系统化.单击此处添加标题一、训练体悟(先独立思考完成,再小组交流;其中打*题选做)
1.数轴上到原点的距离为2的点所表示的数是________
2.若 是一个完全平方式,那么m的值是_________
3.函数 与x轴只有一个交点,则a的值是_______
4.已知等腰三角形的一条边长为6,另一条边长为4,则该等腰三角形的周长等于_______
*5.在半径为1的⊙O中,弦AB= ,AC= ,则∠BAC的度数是_______中考复习《分类讨论》的设计二、方法揭示(先独立思考并作简单记录,后小组交流呈现)
在交流完成上述题目并解决后,请你思考下列问题:
1.上述问题中,引起问题的不同结果的原因各是什么?
2.在已学的初中知识范围内,你还碰到过哪些类似的问题?
3.解决这类问题的数学思想方法是什么?应用它解决问题需用注意什么问题?多题归一从有限的问题解决中体会方法的应用,再联系已学的知识范围内的相同类型,寻找问题和方法的共同特征,揭示出分类讨论数学思想方法的本质内涵单击此处添加标题 从案例中可总结多题归一有如下四个步骤:
1.发现多题之间的共同特征,并作出描述;
2.关注差别,研究这类问题大致有几种类型;
3.深入讨论这类问题的本质,形成可操作的解题模块;
4.反思这类题所蕴涵的数学思想方法.
从形式上看,多题归一可以借助图、表、框图等.在实践中,注重师生的共同参与.多题归一单击此处添加标题 任何一个创造过程,都是发散思维和聚合思维的完美结合。而多解、多题归一的训练,则是培养聚合性思维的重要途径。很多数学题,虽然题型各异,研究对象不同,但问题的实质相同,若能对这些“型异质同”或“型近质同”的问题归类分析,抓住共同的本质特征,掌握解答此类问题的规律,就能达到举一反三、事半功倍的教学效果,从而摆脱“题海”泛舟的苦恼。多题归一“一生万物,万物归一” 初三复习不是在同一水平上的简单重复,要创造性地将知识、能力和思想方法在更多的新情境、更高的层次中不断地、反复地渗透,才能达到螺旋式的再认识,再深化乃至升华的结果. 在复习过程中,课堂教学是充满灵感,充满激情,充满理想的过程,不能仅仅停留在习题本身所传达的文字信息上,应重视对已有题型的挖掘、延伸,使学生加深对原题解法的理解,提高学生解题的灵活性,更应注重激发兴趣和求知欲,注重意识、思想和认识方法的渗透和能力的培养.敬请大家
批评指正谢谢!
同课章节目录
