2016市数学中考复习会议资料背景不同,追本溯圆课件(11张ppt)
文档属性
| 名称 | 2016市数学中考复习会议资料背景不同,追本溯圆课件(11张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-22 00:00:00 | ||
图片预览


文档简介
课件11张PPT。华茂外国语学校 徐啸晖背景不同,追本溯“圆”——直角坐标背景下圆的复习
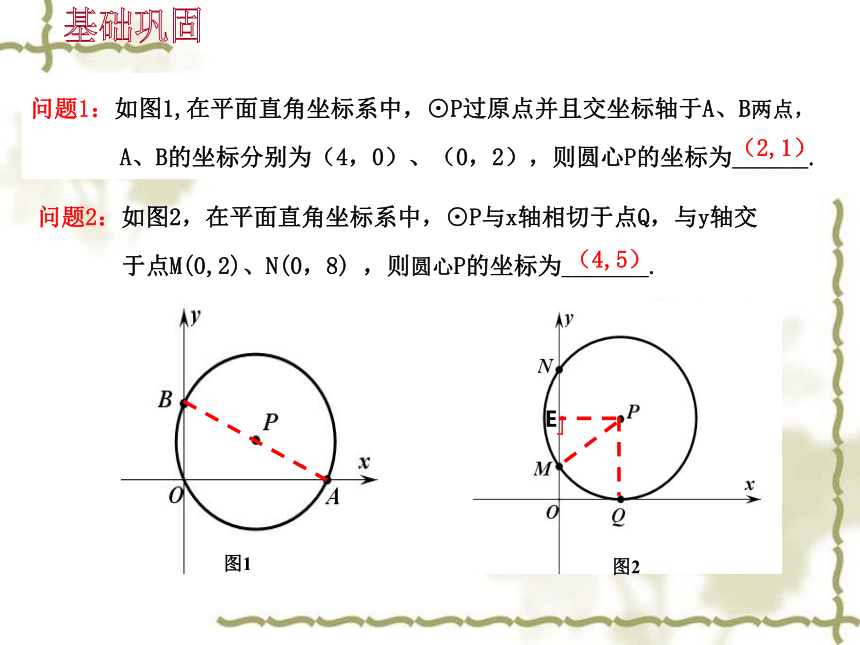
图1
图2问题1:如图1,在平面直角坐标系中,⊙P过原点并且交坐标轴于A、B两点,
A、B的坐标分别为(4,0)、(0,2),则圆心P的坐标为_______.问题2:如图2,在平面直角坐标系中,⊙P与x轴相切于点Q,与y轴交
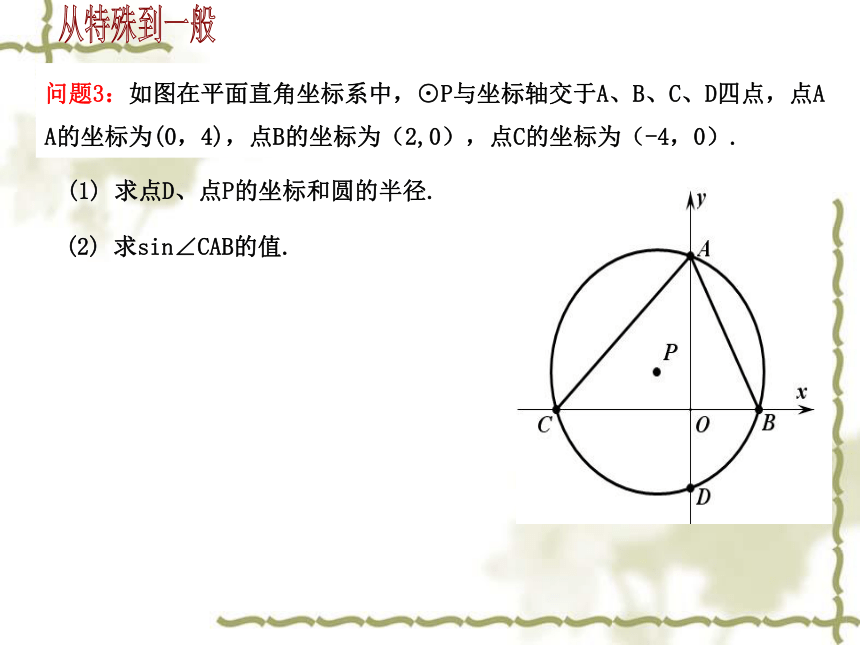
于点M(0,2)、N(0,8) ,则圆心P的坐标为________.基础巩固(2,1)(4,5)问题3:如图在平面直角坐标系中,⊙P与坐标轴交于A、B、C、D四点,点A
A的坐标为(0,4),点B的坐标为(2,0),点C的坐标为(-4,0).(1) 求点D、点P的坐标和圆的半径.(2) 求sin∠CAB的值.从特殊到一般一路闯关,你敢来吗?go问题4:如图,在平面直角坐标系中,点M在x轴正半轴上,⊙M交x轴于
A,B两点,交y轴于C,D两点,已知A的坐标为(-2,0),C的坐标为(0,4).
(1)求⊙M的半径第一关问题4:如图,在平面直角坐标系中,点M在x轴正半轴上,⊙M交x轴于
A,B两点,交y轴于C,D两点,已知A的坐标为(-2,0),C的坐标为(0,4).
(2)过A、B、C三点作抛物线,求抛物线的解析式.第二关问题4:如图,在平面直角坐标系中,点M在x轴正半轴上,⊙M交x轴于
A,B两点,交y轴于C,D两点,已知A的坐标为(-2,0),C的坐标为(0,4).
(3)设平行于x轴的直线交抛物线于E,F两点,问:是否存在以线段EF
为直径的圆,恰好与x轴相切?若存在,求出该圆的半径,若不存在,
请说明理由?第三关问题4:如图,在平面直角坐标系中,点M在x轴正半轴上,⊙M交x轴于
A,B两点,交y轴于C,D两点,已知A的坐标为(-2,0),C的坐标为(0,4).
(4)过点C作圆的切线交x轴于点G
①求G点坐标
②当动点K在⊙M的圆上运动时(不于A,B两点重合),求证△MKO∽△MGK. 第四关问题4:如图,在平面直角坐标系中,点M在x轴正半轴上,⊙M交x轴于
A,B两点,交y轴于C,D两点,已知A的坐标为(-2,0),C的坐标为(0,4).
(5)点Q是 上一点,使 ,P为x轴下方半圆上一动点,连结PQ,
交CB于R,当△CQR为等腰三角形时,直接写出PQ的长.第五关 在本节课中,我们学习了……回顾反思在直角坐标系的背景下进一步巩固圆的核心概念以及常见的方法.数学思想:转化、分类讨论、数形结合等
图1
图2问题1:如图1,在平面直角坐标系中,⊙P过原点并且交坐标轴于A、B两点,
A、B的坐标分别为(4,0)、(0,2),则圆心P的坐标为_______.问题2:如图2,在平面直角坐标系中,⊙P与x轴相切于点Q,与y轴交
于点M(0,2)、N(0,8) ,则圆心P的坐标为________.基础巩固(2,1)(4,5)问题3:如图在平面直角坐标系中,⊙P与坐标轴交于A、B、C、D四点,点A
A的坐标为(0,4),点B的坐标为(2,0),点C的坐标为(-4,0).(1) 求点D、点P的坐标和圆的半径.(2) 求sin∠CAB的值.从特殊到一般一路闯关,你敢来吗?go问题4:如图,在平面直角坐标系中,点M在x轴正半轴上,⊙M交x轴于
A,B两点,交y轴于C,D两点,已知A的坐标为(-2,0),C的坐标为(0,4).
(1)求⊙M的半径第一关问题4:如图,在平面直角坐标系中,点M在x轴正半轴上,⊙M交x轴于
A,B两点,交y轴于C,D两点,已知A的坐标为(-2,0),C的坐标为(0,4).
(2)过A、B、C三点作抛物线,求抛物线的解析式.第二关问题4:如图,在平面直角坐标系中,点M在x轴正半轴上,⊙M交x轴于
A,B两点,交y轴于C,D两点,已知A的坐标为(-2,0),C的坐标为(0,4).
(3)设平行于x轴的直线交抛物线于E,F两点,问:是否存在以线段EF
为直径的圆,恰好与x轴相切?若存在,求出该圆的半径,若不存在,
请说明理由?第三关问题4:如图,在平面直角坐标系中,点M在x轴正半轴上,⊙M交x轴于
A,B两点,交y轴于C,D两点,已知A的坐标为(-2,0),C的坐标为(0,4).
(4)过点C作圆的切线交x轴于点G
①求G点坐标
②当动点K在⊙M的圆上运动时(不于A,B两点重合),求证△MKO∽△MGK. 第四关问题4:如图,在平面直角坐标系中,点M在x轴正半轴上,⊙M交x轴于
A,B两点,交y轴于C,D两点,已知A的坐标为(-2,0),C的坐标为(0,4).
(5)点Q是 上一点,使 ,P为x轴下方半圆上一动点,连结PQ,
交CB于R,当△CQR为等腰三角形时,直接写出PQ的长.第五关 在本节课中,我们学习了……回顾反思在直角坐标系的背景下进一步巩固圆的核心概念以及常见的方法.数学思想:转化、分类讨论、数形结合等
同课章节目录
