2016宁波市数学中考复习会议资料:二次函数的图像变换课件(14张ppt)
文档属性
| 名称 | 2016宁波市数学中考复习会议资料:二次函数的图像变换课件(14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 919.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-22 00:00:00 | ||
图片预览





文档简介
课件14张PPT。2016年中考数学专题复习课宁波市李兴贵中学 章 民
2016年3月22日 取 精 髓 展 本 质
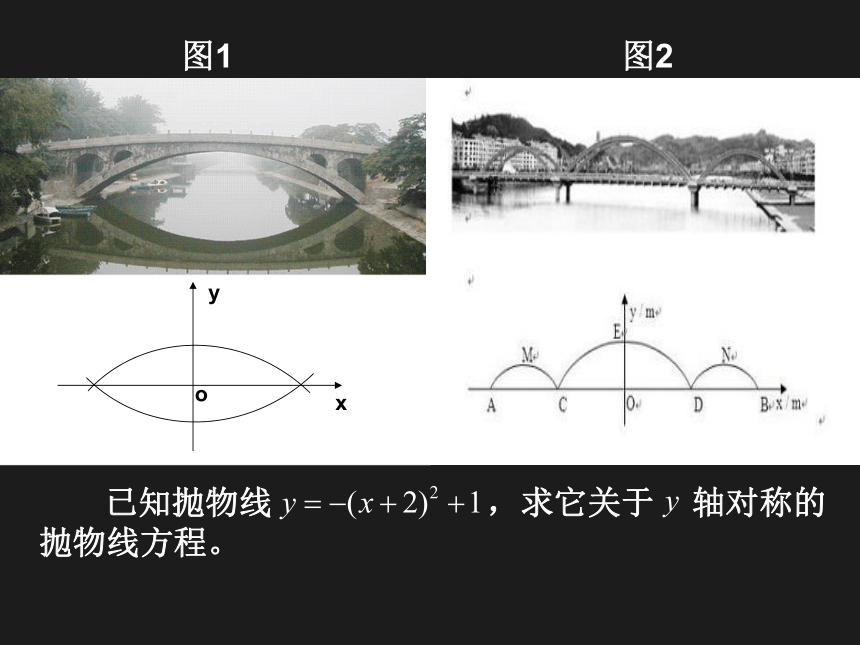
——二次函数图像的变换规律探究及运用图1图2 已知抛物线 ,求它关于 轴对称的
抛物线方程。
已知抛物线 ,其中 是常数,对称轴为
直线 ,该抛物线沿 轴向上平移多少个单位长度后,
得到的抛物线与 轴只有一个公共点?(2015·宁波)(2015年·绍兴) 如果一种变换是将抛物线向右平移2个单位或
向上平移1个单位,我们把这种变换称为抛物线的
简单变换。已知抛物线经过两次简单变换后的一条
抛物线是 ,
则原抛物线的解析式不可能的是( )
B.
C. D.
(2015·衢州)(定义)如果二次函数
与 满足
则称这两个函数互为“旋转函数”.
(1)求函数 的“旋转函数”;
(2)若函数 与 互为
“旋转函数”,求 的值;
(2015·衢州)(定义)如果二次函数
与 满足
则称这两个函数互为“旋转函数”.
(3)已知函数 的图像与 轴交于点A,B两
点,与 轴交于点C,点A,B,C关于原点的对称点分别是
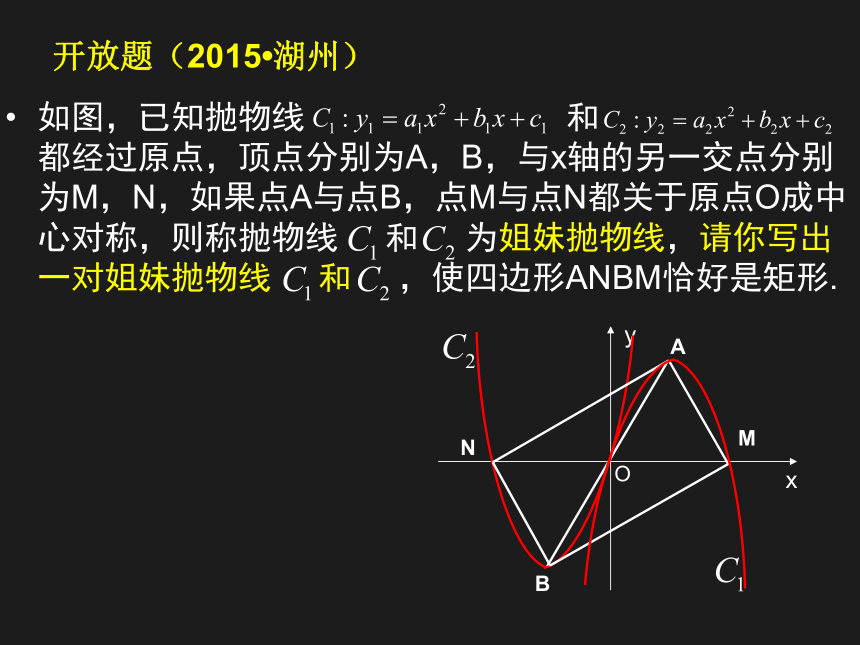
试证明经过点 的二次函数与函数 互为“旋转函数”.如图,已知抛物线 和 都经过原点,顶点分别为A,B,与x轴的另一交点分别为M,N,如果点A与点B,点M与点N都关于原点O成中心对称,则称抛物线 和 为姐妹抛物线,请你写出一对姐妹抛物线 和 ,使四边形ANBM恰好是矩形.开放题(2015?湖州) 复习建议立足考试说明;
研究例卷样卷。
把握中考方向;
保持良好心态。谢谢大家!(2015·莆田) 抛物线 ,若 满足 ,
则称抛物线 为“恒定”抛物线。(1)求证:“恒定抛物线” 必经过 轴上的一个
定点A;(2)已知“恒定”抛物线 的顶点为P,与 轴另一个交
点为B;是否存在以Q为顶点,与 轴另一个交点为C的“恒定”
抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,
求出抛物线解析式;若不存在,请说明理由。(2015·贵州六盘水)
如图14,已知图①中抛物线 经过点
C(0,-1),D(-1,0),E(1,0). (2015年·杭州)设函数 .
(1)当 时的函数 的图象如图所示,请你在同一
直角坐标系中画出当 时函数的图象;
(2)根据图象,写出你发现的一条结论;
(3)将函数 的图象向左平移4个单位,再向下平移2个单位,
得到函数 的图象,求函数 的最小值.(2015·陕西)在平面直角坐标系中,抛物线 的顶点为M,
与 轴交于点A,B,与 轴交于点C。
(1)求点A,B,C的坐标;
(2)求抛物线 关于原点对称的抛物线解析式;
(3)设(2)中所求抛物线的顶点为 ,与 轴交于 两点,
与 轴交于 点,在以 这八个点中的
四个点为顶点的平行四边形中,求其中一个不是菱形的平行
四边形的面积。
2016年3月22日 取 精 髓 展 本 质
——二次函数图像的变换规律探究及运用图1图2 已知抛物线 ,求它关于 轴对称的
抛物线方程。
已知抛物线 ,其中 是常数,对称轴为
直线 ,该抛物线沿 轴向上平移多少个单位长度后,
得到的抛物线与 轴只有一个公共点?(2015·宁波)(2015年·绍兴) 如果一种变换是将抛物线向右平移2个单位或
向上平移1个单位,我们把这种变换称为抛物线的
简单变换。已知抛物线经过两次简单变换后的一条
抛物线是 ,
则原抛物线的解析式不可能的是( )
B.
C. D.
(2015·衢州)(定义)如果二次函数
与 满足
则称这两个函数互为“旋转函数”.
(1)求函数 的“旋转函数”;
(2)若函数 与 互为
“旋转函数”,求 的值;
(2015·衢州)(定义)如果二次函数
与 满足
则称这两个函数互为“旋转函数”.
(3)已知函数 的图像与 轴交于点A,B两
点,与 轴交于点C,点A,B,C关于原点的对称点分别是
试证明经过点 的二次函数与函数 互为“旋转函数”.如图,已知抛物线 和 都经过原点,顶点分别为A,B,与x轴的另一交点分别为M,N,如果点A与点B,点M与点N都关于原点O成中心对称,则称抛物线 和 为姐妹抛物线,请你写出一对姐妹抛物线 和 ,使四边形ANBM恰好是矩形.开放题(2015?湖州) 复习建议立足考试说明;
研究例卷样卷。
把握中考方向;
保持良好心态。谢谢大家!(2015·莆田) 抛物线 ,若 满足 ,
则称抛物线 为“恒定”抛物线。(1)求证:“恒定抛物线” 必经过 轴上的一个
定点A;(2)已知“恒定”抛物线 的顶点为P,与 轴另一个交
点为B;是否存在以Q为顶点,与 轴另一个交点为C的“恒定”
抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,
求出抛物线解析式;若不存在,请说明理由。(2015·贵州六盘水)
如图14,已知图①中抛物线 经过点
C(0,-1),D(-1,0),E(1,0). (2015年·杭州)设函数 .
(1)当 时的函数 的图象如图所示,请你在同一
直角坐标系中画出当 时函数的图象;
(2)根据图象,写出你发现的一条结论;
(3)将函数 的图象向左平移4个单位,再向下平移2个单位,
得到函数 的图象,求函数 的最小值.(2015·陕西)在平面直角坐标系中,抛物线 的顶点为M,
与 轴交于点A,B,与 轴交于点C。
(1)求点A,B,C的坐标;
(2)求抛物线 关于原点对称的抛物线解析式;
(3)设(2)中所求抛物线的顶点为 ,与 轴交于 两点,
与 轴交于 点,在以 这八个点中的
四个点为顶点的平行四边形中,求其中一个不是菱形的平行
四边形的面积。
同课章节目录
