数学八年级下人教新课标18.1 平行四边形 (第1课时)18.1.1平行四边形的性质(1) 课件
文档属性
| 名称 | 数学八年级下人教新课标18.1 平行四边形 (第1课时)18.1.1平行四边形的性质(1) 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 239.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-24 15:10:13 | ||
图片预览



文档简介
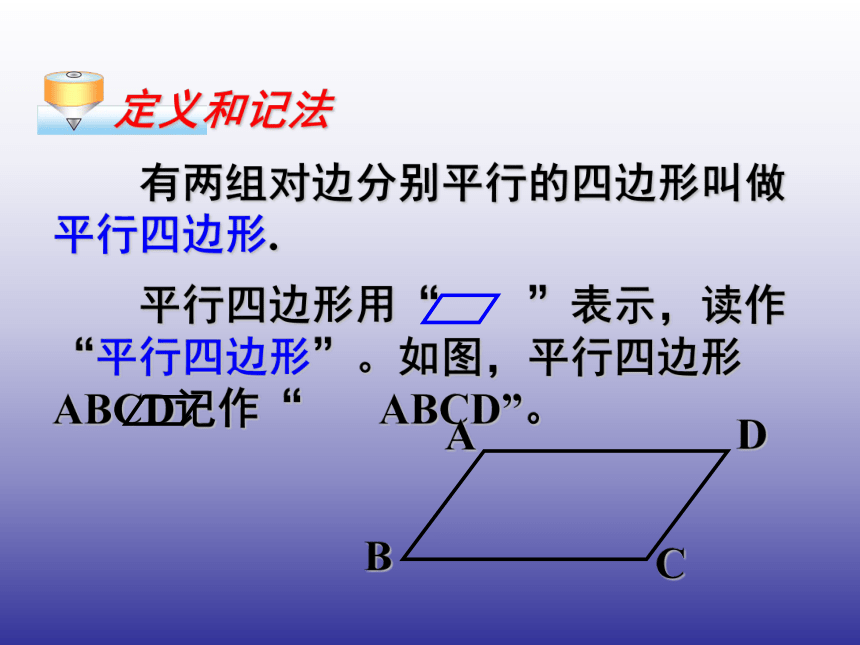
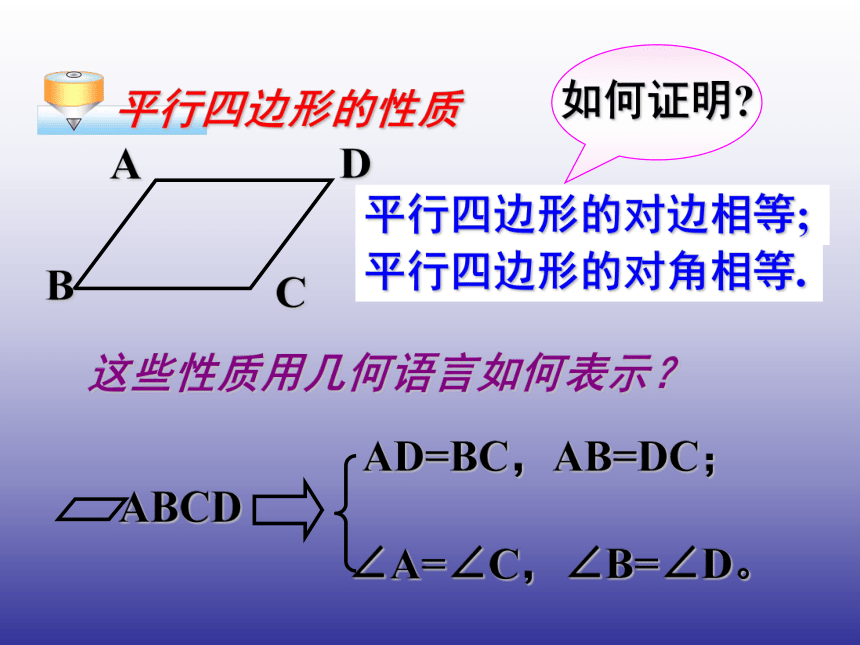
课件14张PPT。人教版八年级(下册)第十八章四边形18.1.1 平行四边形的性质(1)18.1平行四边形(第1课时)复习回顾1、四边形的内角和为 ,外角和为 .2、已知:a∥b,c∥d则所以∠1=∠3 ( )。∠3+∠4= ( ),∠1+∠4= ( ),∠2=∠3 ( ),∠1=∠2( ), 平行四边形是我们常见的图形,小区的伸缩门、庭院的竹篱笆等,都是平行四边形的形象。定义和记法 有两组对边分别平行的四边形叫做平行四边形. 由平行四边形的定义,我们知道平行四边形的两组对边分别平行。除此之外,平行四边形还有什么特征呢? 根据定义画一个平行四边形,观察这个四边形,除了“两组对边分别平行”以外,它的边、角之间有什么关系呢? 度量一下,是不是和你的猜想一致?平行四边形的对边相等;平行四边形的对角相等.AD=BC,AB=DC;∠A=∠C,∠B=∠D。平行四边形的性质这些性质用几何语言如何表示?如何证明?求证:平行四边形的对边相等、对角相等. 分析:先根据题目画图,并写出“已知”与 “求证”。求证:AD=BC,AB=DC;∠A=∠C,∠B=∠D。 分析:要 证的是不在同一三角形的边相等、角相等,可作辅助线,构建全等三角形.证明: 连接AC , 在△ABC和△CDA中,∠1=∠3 (已证),∠2=∠4(已证),AC=CA (公共边),所以△ABC≌△CDA(ASA)。所以AB=CD, BC =AD ,∠B=∠D。 又∠1+∠4=∠2+∠ 3,所以 ∠BAD=∠BCD。所以 ∠1=∠3 , ∠ 2=∠4。因为 AB∥ CD , AD∥ BC,证法一:因为四边形ABCD是平行四边形,
所以AB∥CD,AD∥BC。
所以∠A+∠B=180°,
∠A+∠D=180°。
所以∠B=∠D(同角的补角相等)。证法二 :延长DC到点E。
因为四边形ABCD是平行四边形,
所以AB∥CD,AD∥BC。
所以∠B=∠DCE,
∠DCE=∠D 。
所以∠B=∠D(等量代换)。E1、如图,在平行四边形ABCD中,∠B=50o,求∠C、∠D、∠A的度数.2a+2b练习3、如图, 已知,l1∥l2
⑴如果AB⊥l2,那么AB是否
垂直于l1?为什么? ⑵如果AB⊥l2,CD⊥l2,那么AB是否等于CD?为什么?9100o80o今 日 作 业课本P49习题18.1第1题、第2题。
所以AB∥CD,AD∥BC。
所以∠A+∠B=180°,
∠A+∠D=180°。
所以∠B=∠D(同角的补角相等)。证法二 :延长DC到点E。
因为四边形ABCD是平行四边形,
所以AB∥CD,AD∥BC。
所以∠B=∠DCE,
∠DCE=∠D 。
所以∠B=∠D(等量代换)。E1、如图,在平行四边形ABCD中,∠B=50o,求∠C、∠D、∠A的度数.2a+2b练习3、如图, 已知,l1∥l2
⑴如果AB⊥l2,那么AB是否
垂直于l1?为什么? ⑵如果AB⊥l2,CD⊥l2,那么AB是否等于CD?为什么?9100o80o今 日 作 业课本P49习题18.1第1题、第2题。
