数学八年级下人教新课标18.1 平行四边形 (第3课时)18.1.2平行四边形的判定(1) 课件
文档属性
| 名称 | 数学八年级下人教新课标18.1 平行四边形 (第3课时)18.1.2平行四边形的判定(1) 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 744.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-24 16:03:28 | ||
图片预览


文档简介
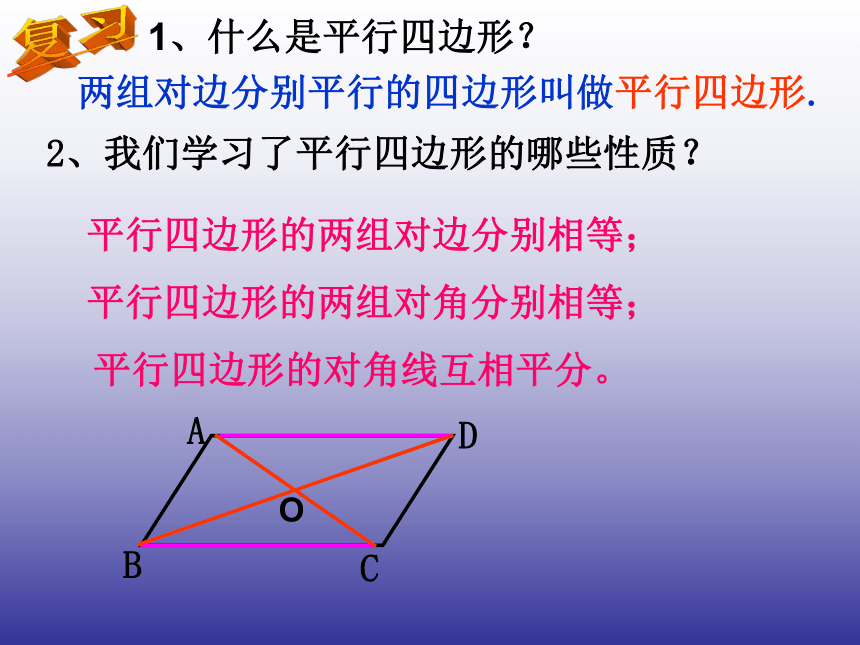
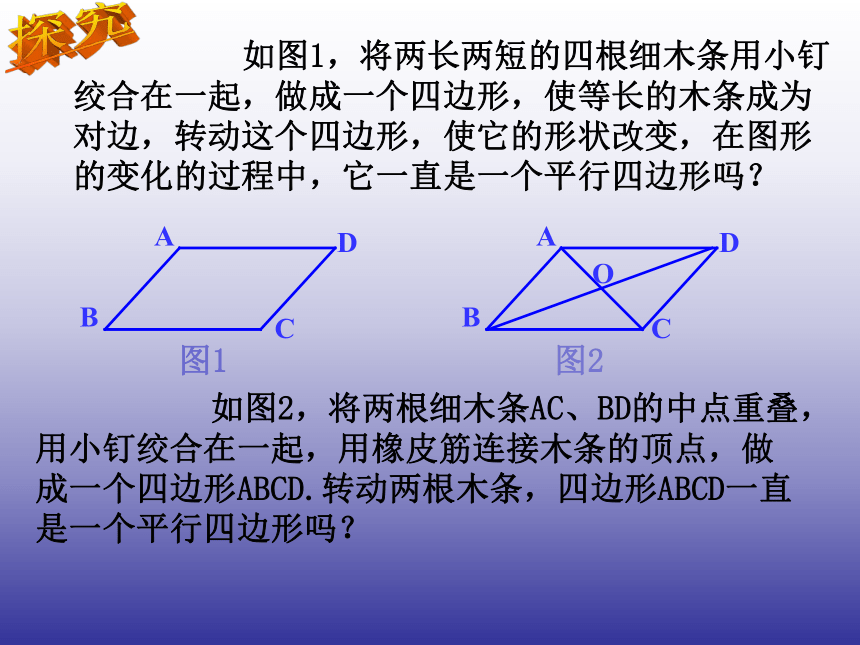
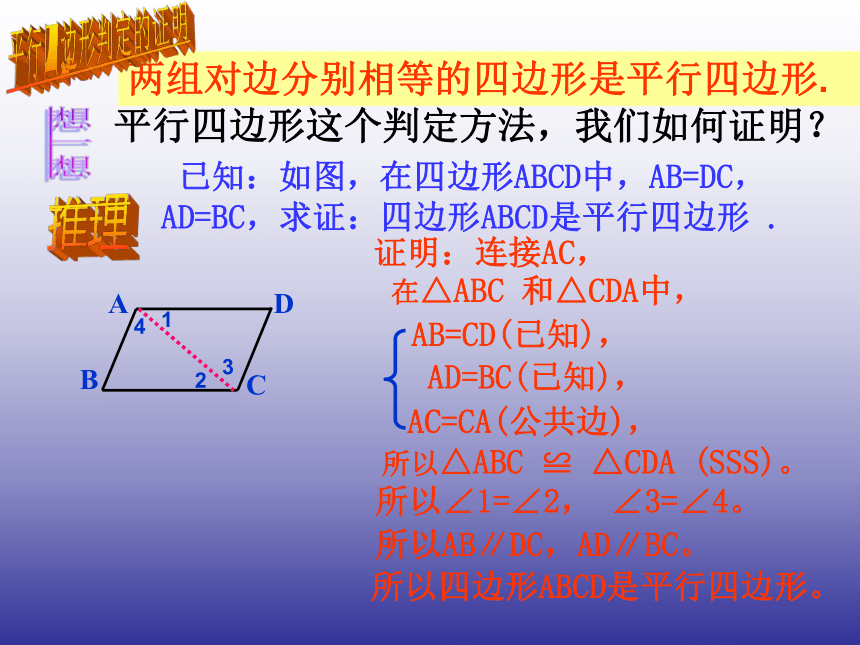
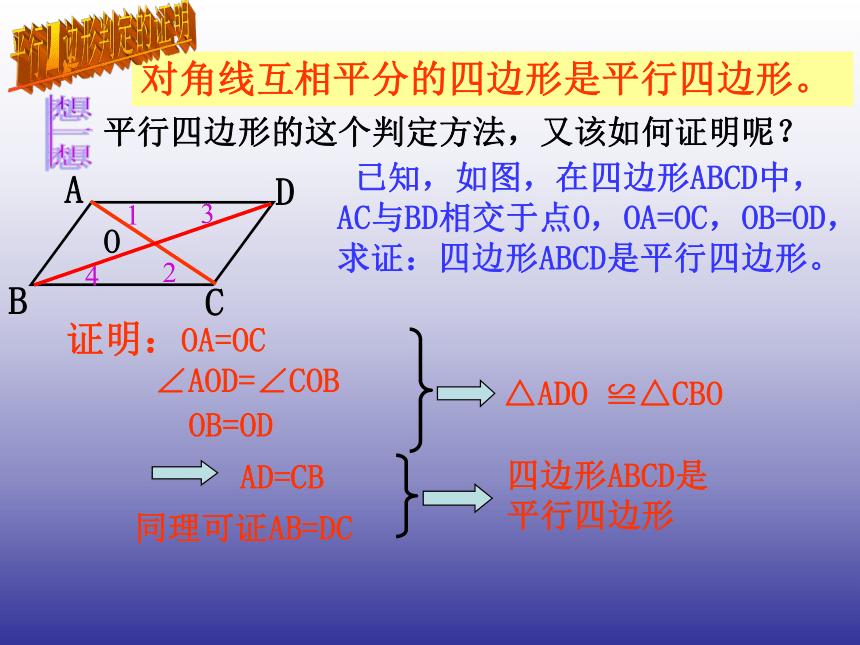
课件12张PPT。人教版八年级(下册)第十八章四边形18.1.2 平行四边形的判定(1)18.1平行四边形(第3课时)复习平行四边形的两组对边分别相等;平行四边形的两组对角分别相等;平行四边形的对角线互相平分。两组对边分别平行的四边形叫做平行四边形.2、我们学习了平行四边形的哪些性质?1、什么是平行四边形?思考平行四边形的两组对边分别相等;平行四边形的两组对角分别相等;我们得到的这些逆命题都成立吗?我们一起探讨一下吧:平行四边形的对角线互相平分。思考:我们已经学习了平行四边形的这些性质,那么它们的逆命题各是什么呢?两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形。两组对边分别相等的四边形是平行四边形;探究 如图1,将两长两短的四根细木条用小钉绞合在一起,做成一个四边形,使等长的木条成为对边,转动这个四边形,使它的形状改变,在图形的变化的过程中,它一直是一个平行四边形吗? 如图2,将两根细木条AC、BD的中点重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD.转动两根木条,四边形ABCD一直是一个平行四边形吗? 图1图2两组对边分别相等的四边形是平行四边形.想一想平行四边形这个判定方法,我们如何证明?推理 证明:连接AC,所以AB∥DC,AD∥BC。4123所以∠1=∠2, ∠3=∠4。AC=CA(公共边),所以△ABC ≌ △CDA (SSS)。 AD=BC(已知),平行四边形判定的证明 已知:如图,在四边形ABCD中,AB=DC,AD=BC,求证:四边形ABCD是平行四边形 .AB=CD(已知),在△ABC 和△CDA中, 所以四边形ABCD是平行四边形。对角线互相平分的四边形是平行四边形。 已知,如图,在四边形ABCD中,AC与BD相交于点O,OA=OC,OB=OD,求证:四边形ABCD是平行四边形。同理可证AB=DC△ADO ≌△CBO AD=CBOA=OC 平行四边形判定的证明证明:想一想平行四边形的这个判定方法,又该如何证明呢? OB=OD∠AOD=∠COB四边形ABCD是平行四边形两组对角分别相等的四边形是平行四边形.想一想平行四边形这个判定方法,又怎么证明呢?推理 证明:所以AB∥DC,AD∥BC。∠A+∠B+∠C+∠D=360°。 平行四边形判定的证明 已知:如图,在四边形ABCD中,∠A=∠C, ∠ B=∠D ,求证:四边形ABCD是平行四边形 .在四边形ABCD中, 所以四边形ABCD是平行四边形。因为∠A=∠C, ∠B=∠D,所以∠A+∠D=180°,
∠A+∠B=180°。归纳两组对边分别平行的四边形是平行四边形(定义);两组对角分别相等的四边形是平行四边形;AD∥BC AB∥DCAD=BC AB=DC∠BAD=∠BCD ∠ABC=∠ADC四边形ABCD是平行四边形如图,用符号表示如下:平行四边形有哪些判定方法?对角线互相平分的四边形是平行四边形。OA=OC OB=OD两组对边分别相等的四边形是平行四边形;四边形ABCD是平行四边形四边形ABCD是平行四边形四边形ABCD是平行四边形又OB=OD,证明:因为四边形ABCD是平行四边形,所以OA=OC, OB=OD。因为AE=CF,所以OE=OF。例题所以四边形BFDE是平行四边形。你还有其他的证明方法吗?练习 如图,AB=DC=EF,AD=BC,DE=CF,图中有哪些互相平行的线段?解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF AD∥BC AB=DC AD=BC四边形ABCD是平行四边形AB∥DCDC∥EF DC=EF DE=CF四边形CDEF是平行四边形DE∥CFAB∥ DC∥EF理由如下:谈谈你在这节课中,有什么收获?小结今 日 作 业课本P50习题18.1第4题,第5题。
∠A+∠B=180°。归纳两组对边分别平行的四边形是平行四边形(定义);两组对角分别相等的四边形是平行四边形;AD∥BC AB∥DCAD=BC AB=DC∠BAD=∠BCD ∠ABC=∠ADC四边形ABCD是平行四边形如图,用符号表示如下:平行四边形有哪些判定方法?对角线互相平分的四边形是平行四边形。OA=OC OB=OD两组对边分别相等的四边形是平行四边形;四边形ABCD是平行四边形四边形ABCD是平行四边形四边形ABCD是平行四边形又OB=OD,证明:因为四边形ABCD是平行四边形,所以OA=OC, OB=OD。因为AE=CF,所以OE=OF。例题所以四边形BFDE是平行四边形。你还有其他的证明方法吗?练习 如图,AB=DC=EF,AD=BC,DE=CF,图中有哪些互相平行的线段?解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF AD∥BC AB=DC AD=BC四边形ABCD是平行四边形AB∥DCDC∥EF DC=EF DE=CF四边形CDEF是平行四边形DE∥CFAB∥ DC∥EF理由如下:谈谈你在这节课中,有什么收获?小结今 日 作 业课本P50习题18.1第4题,第5题。
