数学八年级下人教新课标18.2 特殊平行四边形 (第1课时)18.2.1矩形(矩形的性质) 课件
文档属性
| 名称 | 数学八年级下人教新课标18.2 特殊平行四边形 (第1课时)18.2.1矩形(矩形的性质) 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 852.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-24 16:11:27 | ||
图片预览


文档简介
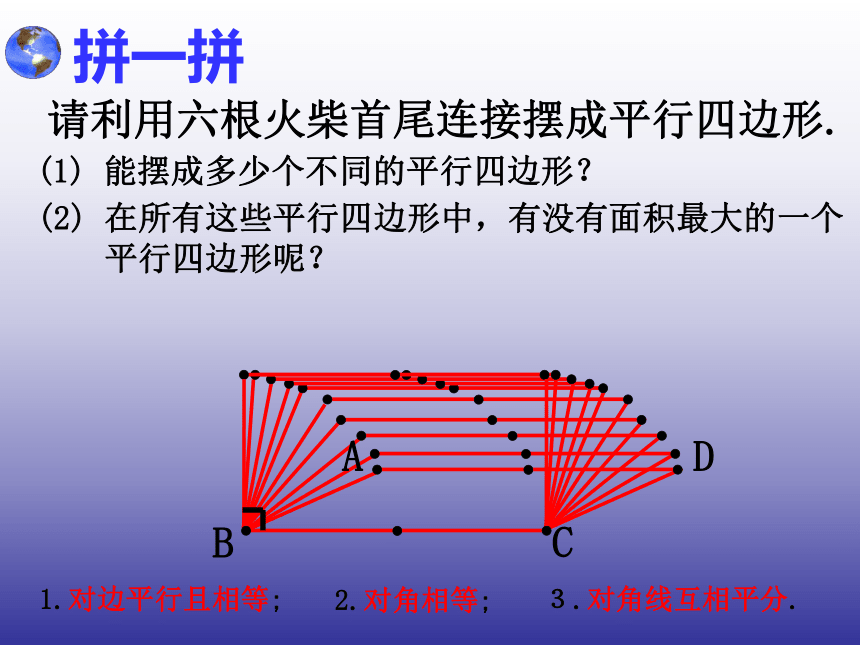
课件12张PPT。人教版八年级(下册)第十八章四边形矩形的性质18.2 特殊的平行四边形(第1课时)18.2.1 矩形拼一拼 请利用六根火柴首尾连接摆成平行四边形. (1) 能摆成多少个不同的平行四边形? (2) 在所有这些平行四边形中,有没有面积最大的一个
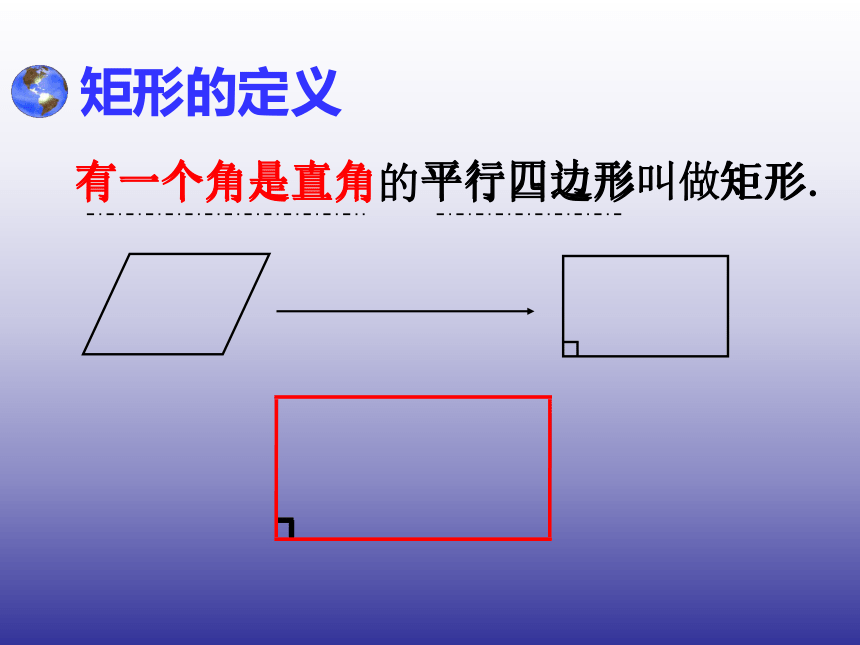
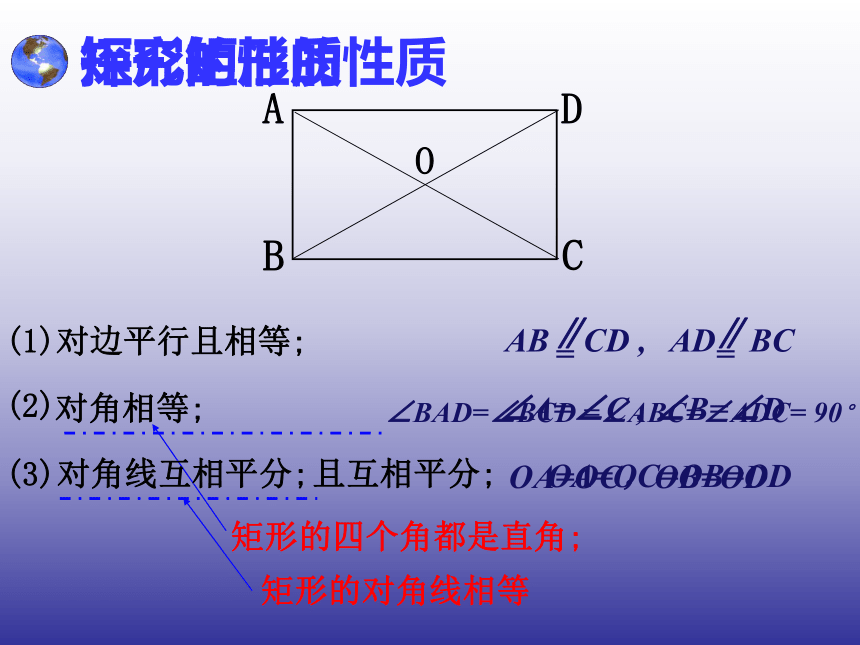
平行四边形呢?1.对边平行且相等;2.对角相等;3.对角线互相平分.平行四边形 有一个角是直角的平行四边形矩形的定义叫做矩形.有一个角是直角矩形 矩形的性质∠BAD=∠BCD =∠ABC=∠ADC= 90°探究矩形的性质O(1)对边平行且相等;(2) (3)∠A=∠C , ∠B=∠DOA=OC,OB=OD矩形的四个角都是直角;矩形的对角线相等对角相等;对角线互相平分;且互相平分;OA=OC=OB=OD试一试1.矩形具有而一般平行四边形不具有的性
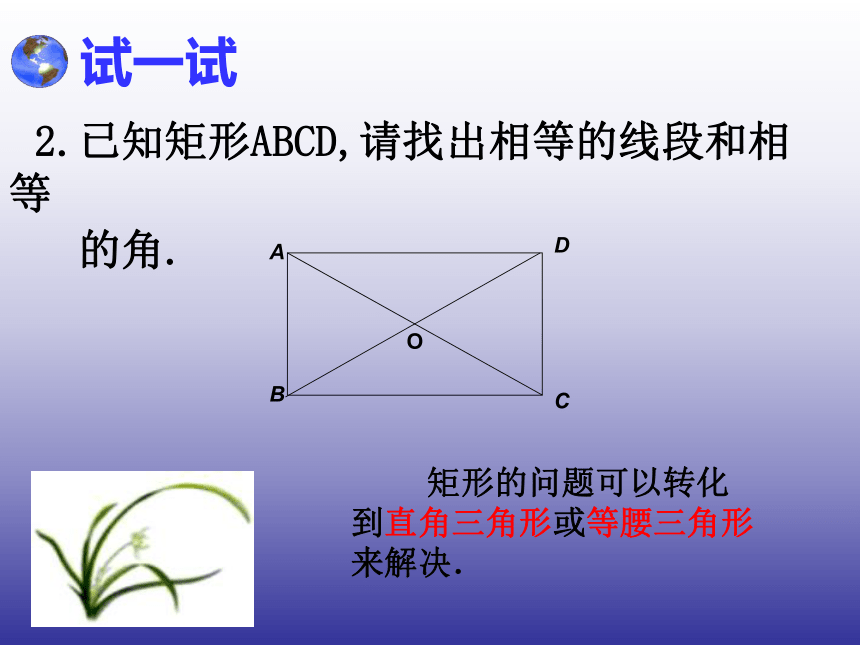
质是 ( )。 C试一试2.已知矩形ABCD,请找出相等的线段和相等
的角. 矩形的问题可以转化到直角三角形或等腰三角形来解决. 已知:在Rt△ABC中,∠ABC=900,BO是AC上的中线.
求证: BO = AC.
OD证明: 延长BO至点D,使OD=BO,
连接AD、DC.因为AO=OC, BO=OD,
所以四边形ABCD是平行四边形.因为∠ABC=900,所以AC=BD。再探新知推论:
直角三角形斜边上的中线
等于斜边的一半. O例1 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长? 解:因为四边形ABCD是矩形,
所以AC与BD相等且互相平分。
所以 OA=OB。
因为∠AOB=60°,
所以△AOB是等边三角形。
所以OA=AB=4(㎝)。
所以矩形的对角线长 AC=BD=2OA=8(㎝)。方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形. 练一练 已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.(1)若BD=3㎝,则AC=______ ㎝;
(2)若∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝.6510本课小结矩形的四个角都是直角.※ 矩形的性质定理1矩形的对角线相等.※ 矩形的性质定理2※ 推 论 直角三角形斜边上的中线等于斜边的一半.今 日 作 业课本P60练习第2题,第3题。
平行四边形呢?1.对边平行且相等;2.对角相等;3.对角线互相平分.平行四边形 有一个角是直角的平行四边形矩形的定义叫做矩形.有一个角是直角矩形 矩形的性质∠BAD=∠BCD =∠ABC=∠ADC= 90°探究矩形的性质O(1)对边平行且相等;(2) (3)∠A=∠C , ∠B=∠DOA=OC,OB=OD矩形的四个角都是直角;矩形的对角线相等对角相等;对角线互相平分;且互相平分;OA=OC=OB=OD试一试1.矩形具有而一般平行四边形不具有的性
质是 ( )。 C试一试2.已知矩形ABCD,请找出相等的线段和相等
的角. 矩形的问题可以转化到直角三角形或等腰三角形来解决. 已知:在Rt△ABC中,∠ABC=900,BO是AC上的中线.
求证: BO = AC.
OD证明: 延长BO至点D,使OD=BO,
连接AD、DC.因为AO=OC, BO=OD,
所以四边形ABCD是平行四边形.因为∠ABC=900,所以AC=BD。再探新知推论:
直角三角形斜边上的中线
等于斜边的一半. O例1 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长? 解:因为四边形ABCD是矩形,
所以AC与BD相等且互相平分。
所以 OA=OB。
因为∠AOB=60°,
所以△AOB是等边三角形。
所以OA=AB=4(㎝)。
所以矩形的对角线长 AC=BD=2OA=8(㎝)。方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形. 练一练 已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.(1)若BD=3㎝,则AC=______ ㎝;
(2)若∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝.6510本课小结矩形的四个角都是直角.※ 矩形的性质定理1矩形的对角线相等.※ 矩形的性质定理2※ 推 论 直角三角形斜边上的中线等于斜边的一半.今 日 作 业课本P60练习第2题,第3题。
