数学八年级下人教新课标18.2 特殊平行四边形 (第5课时)18.2.3正方形 课件
文档属性
| 名称 | 数学八年级下人教新课标18.2 特殊平行四边形 (第5课时)18.2.3正方形 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 653.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-24 00:00:00 | ||
图片预览


文档简介
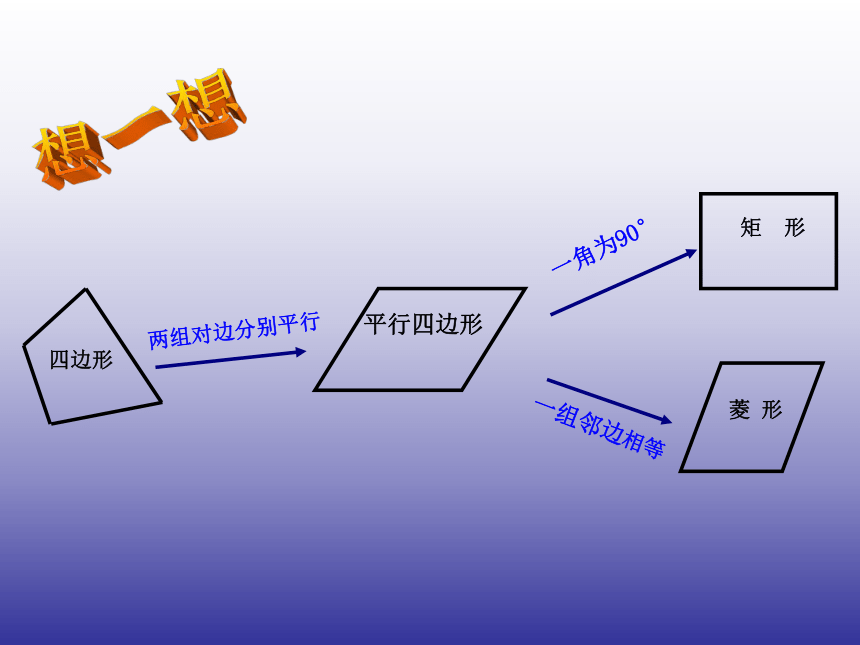
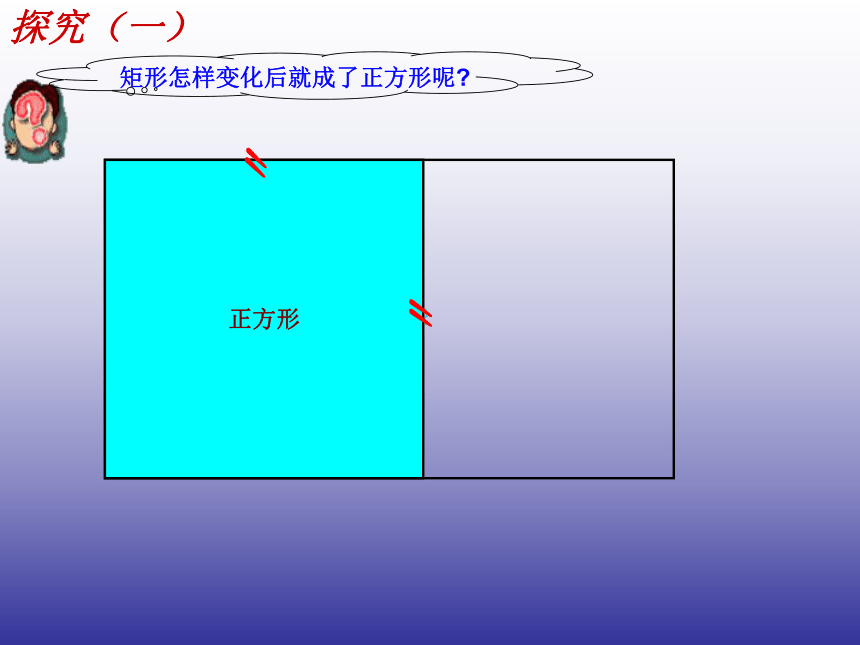
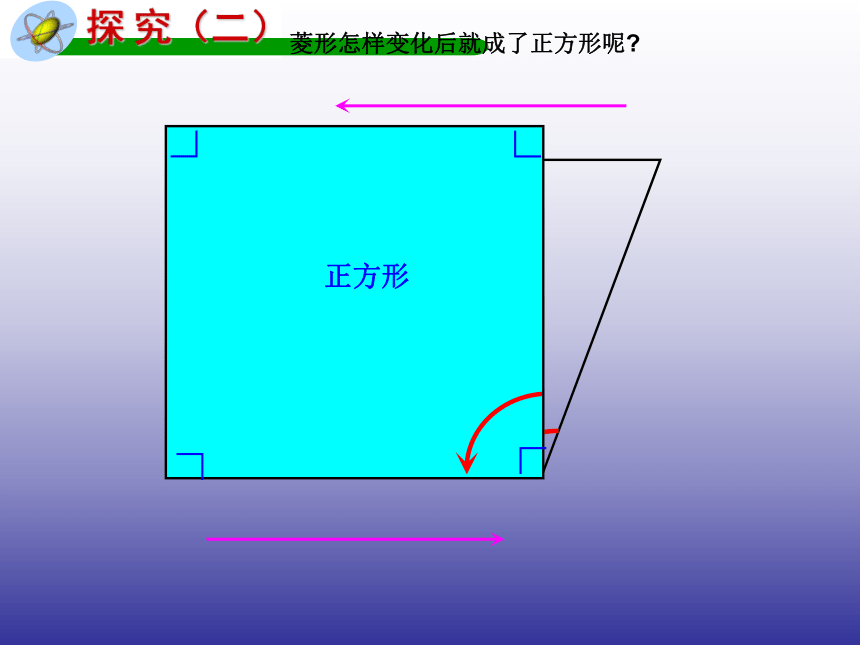
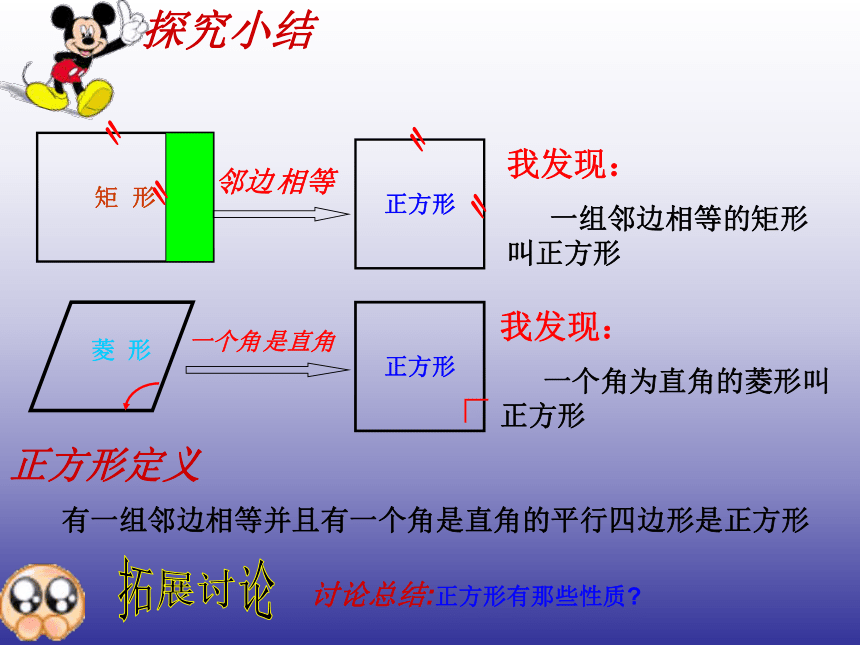
课件15张PPT。人教版八年级(下册)第十八章四边形18.2.3 正方形18.2 特殊的平行四边形(第5课时)想一想矩 形正方形〃〃矩形怎样变化后就成了正方形呢?探究(一)∟∟∟∟正方形菱形怎样变化后就成了正方形呢?探究小结矩 形〃〃正方形邻边相等〃〃我发现:
一组邻边相等的矩形 叫正方形一个角是直角正方形∟我发现:
一个角为直角的菱形叫正方形正方形定义有一组邻边相等并且有一个角是直角的平行四边形是正方形拓展讨论讨论总结:正方形有那些性质?特殊的平行四边形特殊的矩形特殊的菱形1.边:
2.角:
3.对角线:正方形的性质: 四条边都相等
且对边平行;两条对角线互相
垂直平分且相等,
并且每一条对角
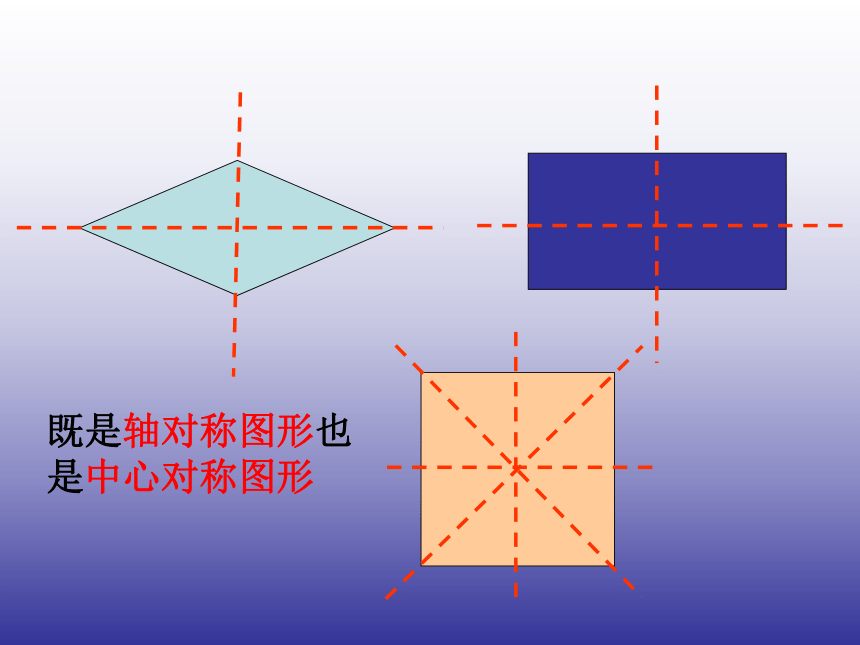
线平分一组对角.四个角都是直角; 既是轴对称图形也
是中心对称图形例 求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.这是一道文字证明题,该怎么做?你会做吗?第一步:根据题意画出图形
第二步:写出已知
第三步:写出求证
第四步:进行证明ADCBO 已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O. 求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
ABCD是一块正方形场地,小华和小芳在AB
边上取定了一点E,经测量知 EC=30m,
EB=10m,这块场地的面积和对角线长分别
是多少(对角线长精确到0.1m)?练一练:ABCDE矩形菱形正方形一组邻边相等一个角是直角平行四边形一组邻边相等、一个角是直角讨论:请用
这四种图形填空A表示:
B表示:
C表示:
D表示:平行四边形、矩形、菱形、正方形平行四边形矩形 (菱形)菱形 (矩形)正方形满足下列条件的四边形是不是正方形:
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形.练一练:既是矩形又是菱形 ——— 正方形判定正方形要准备的条件:平行四边形、一组邻边相等、一个角是直角把一个长方形纸片如图那样折一下,就可以裁出正方形纸片,为什么?如果是一个长方形木板,又如何从中裁出
一个最大的正方形木板呢?实际问题:已知:∠DAB=∠B=∠ADC=
90°,AB=AD.求证:四边形ABCD是正方形取AD=AB,BC=AB即可.小结:特殊的平行四边形、特殊的矩形、特殊的菱形一、什么是正方形:既是矩形又是菱形 ——— 正方形二、正方形有什么性质:具有矩形、菱形、平行四边形的所有性质今 日 作 业课本P61习题19.2第7题,第13题。
一组邻边相等的矩形 叫正方形一个角是直角正方形∟我发现:
一个角为直角的菱形叫正方形正方形定义有一组邻边相等并且有一个角是直角的平行四边形是正方形拓展讨论讨论总结:正方形有那些性质?特殊的平行四边形特殊的矩形特殊的菱形1.边:
2.角:
3.对角线:正方形的性质: 四条边都相等
且对边平行;两条对角线互相
垂直平分且相等,
并且每一条对角
线平分一组对角.四个角都是直角; 既是轴对称图形也
是中心对称图形例 求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.这是一道文字证明题,该怎么做?你会做吗?第一步:根据题意画出图形
第二步:写出已知
第三步:写出求证
第四步:进行证明ADCBO 已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O. 求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
ABCD是一块正方形场地,小华和小芳在AB
边上取定了一点E,经测量知 EC=30m,
EB=10m,这块场地的面积和对角线长分别
是多少(对角线长精确到0.1m)?练一练:ABCDE矩形菱形正方形一组邻边相等一个角是直角平行四边形一组邻边相等、一个角是直角讨论:请用
这四种图形填空A表示:
B表示:
C表示:
D表示:平行四边形、矩形、菱形、正方形平行四边形矩形 (菱形)菱形 (矩形)正方形满足下列条件的四边形是不是正方形:
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形.练一练:既是矩形又是菱形 ——— 正方形判定正方形要准备的条件:平行四边形、一组邻边相等、一个角是直角把一个长方形纸片如图那样折一下,就可以裁出正方形纸片,为什么?如果是一个长方形木板,又如何从中裁出
一个最大的正方形木板呢?实际问题:已知:∠DAB=∠B=∠ADC=
90°,AB=AD.求证:四边形ABCD是正方形取AD=AB,BC=AB即可.小结:特殊的平行四边形、特殊的矩形、特殊的菱形一、什么是正方形:既是矩形又是菱形 ——— 正方形二、正方形有什么性质:具有矩形、菱形、平行四边形的所有性质今 日 作 业课本P61习题19.2第7题,第13题。
