2025年中考数学一轮复习 圆柱、圆锥的计算(含答案)
文档属性
| 名称 | 2025年中考数学一轮复习 圆柱、圆锥的计算(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 423.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-23 00:00:00 | ||
图片预览


文档简介
2025年中考数学一轮复习:圆柱、圆锥的计算
一、单选题
1.某盏路灯照射的空间可以看成如图所示的圆锥,它的高,底面半径,则圆锥的侧面积为( )
A. B. C. D.
2.一个圆锥的底面半径的长为3,母线的长为15,则侧面展开图的面积是( )
A. B. C. D.
3.如图,已知圆锥侧面展开图的扇形面积为,扇形的弧长为,则圆锥的高是( )
A. B. C. D.
4.如图,在△ABC中,∠C =90°,AC>BC,若以AC为底面圆的半径,BC为高的圆锥的侧面积为S1,若以BC为底面圆的半径,AC为高的圆锥的侧面积为S2 ,则( )
A.S1 =S2 B.S1 >S2
C.S1 <S2 D.S1 ,S2的大小大小不能确定
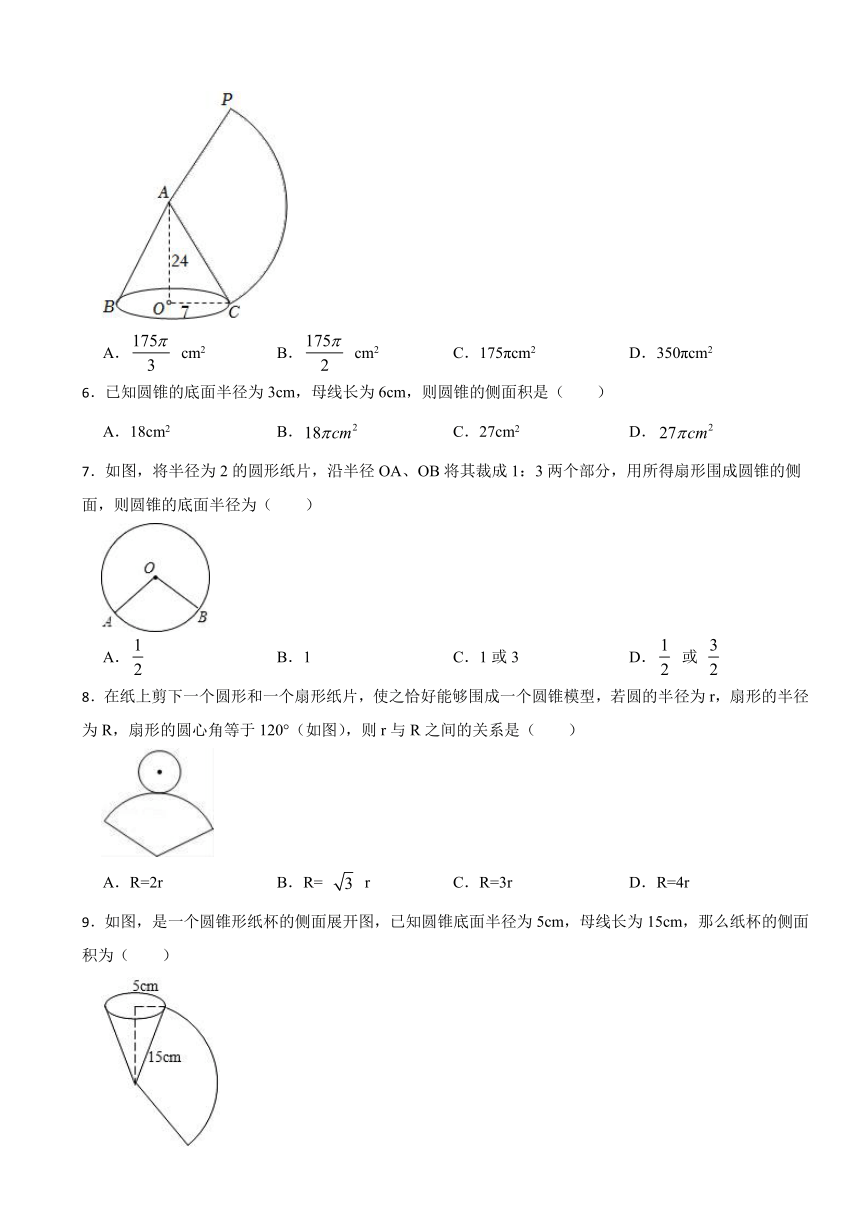
5.如图,圆锥底面圆半径为7cm,高为24cm,则它侧面展开图的面积是( )
A. cm2 B. cm2 C.175πcm2 D.350πcm2
6.已知圆锥的底面半径为3cm,母线长为6cm,则圆锥的侧面积是( )
A.18cm2 B. C.27cm2 D.
7.如图,将半径为2的圆形纸片,沿半径OA、OB将其裁成1:3两个部分,用所得扇形围成圆锥的侧面,则圆锥的底面半径为( )
A. B.1 C.1或3 D. 或
8.在纸上剪下一个圆形和一个扇形纸片,使之恰好能够围成一个圆锥模型,若圆的半径为r,扇形的半径为R,扇形的圆心角等于120°(如图),则r与R之间的关系是( )
A.R=2r B.R= r C.R=3r D.R=4r
9.如图,是一个圆锥形纸杯的侧面展开图,已知圆锥底面半径为5cm,母线长为15cm,那么纸杯的侧面积为( )
A.75πcm2 B.150πcm2 C. D.
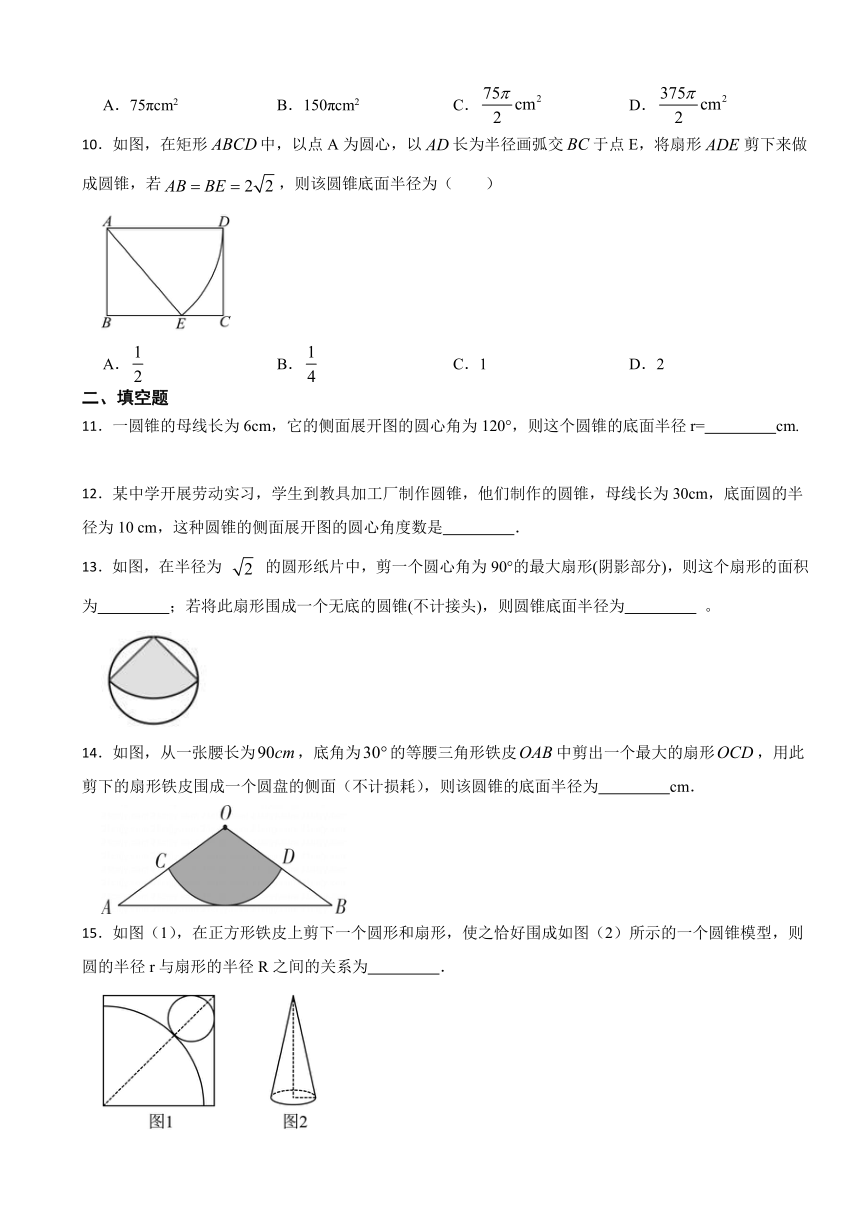
10.如图,在矩形中,以点A为圆心,以长为半径画弧交于点E,将扇形剪下来做成圆锥,若,则该圆锥底面半径为( )
A. B. C.1 D.2
二、填空题
11.一圆锥的母线长为6cm,它的侧面展开图的圆心角为120°,则这个圆锥的底面半径r= cm.
12.某中学开展劳动实习,学生到教具加工厂制作圆锥,他们制作的圆锥,母线长为30cm,底面圆的半径为10 cm,这种圆锥的侧面展开图的圆心角度数是 .
13.如图,在半径为 的圆形纸片中,剪一个圆心角为90°的最大扇形(阴影部分),则这个扇形的面积为 ;若将此扇形围成一个无底的圆锥(不计接头),则圆锥底面半径为 。
14.如图,从一张腰长为,底角为的等腰三角形铁皮中剪出一个最大的扇形,用此剪下的扇形铁皮围成一个圆盘的侧面(不计损耗),则该圆锥的底面半径为 cm.
15.如图(1),在正方形铁皮上剪下一个圆形和扇形,使之恰好围成如图(2)所示的一个圆锥模型,则圆的半径r与扇形的半径R之间的关系为 .
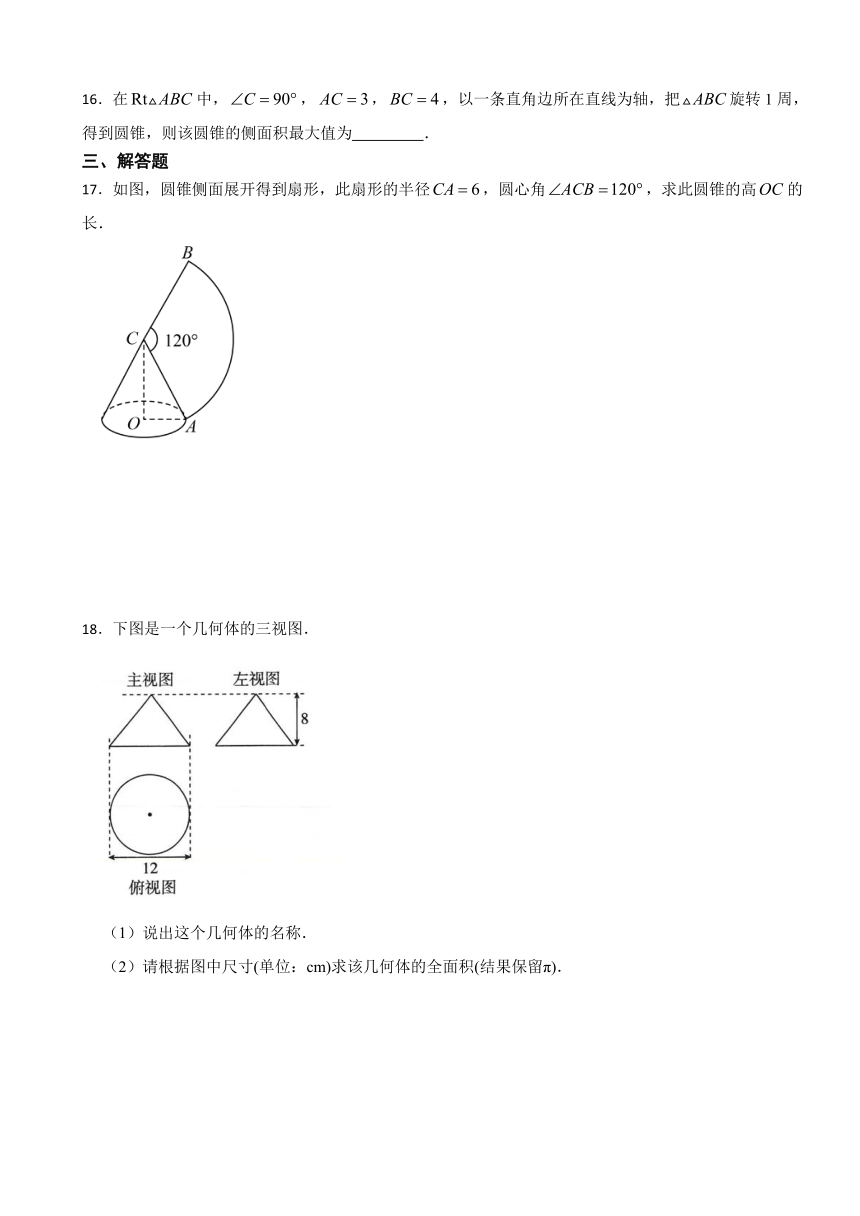
16.在中,,,,以一条直角边所在直线为轴,把旋转1周,得到圆锥,则该圆锥的侧面积最大值为 .
三、解答题
17.如图,圆锥侧面展开得到扇形,此扇形的半径,圆心角,求此圆锥的高的长.
18.下图是一个几何体的三视图.
(1)说出这个几何体的名称.
(2)请根据图中尺寸(单位:cm)求该几何体的全面积(结果保留π).
19.如图1,在等腰三角形ABC中,∠BAC=120°,AD是∠BAC的平分线,且AD=6,以点A为圆心,AD的长为半径画,交AB于点E,交AC于点F.
(1)求由及线段FC,CB,BE围成图形(图1中阴影部分)的面积(结果保留π).
(2)如图2,将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
20.如图所示,在半径为27m的广场中央,点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°,求光源离地面的垂直高度SO.(精确到0.1m;
=1. 414, =1.732, =2.236,以上数据供参考)
21.如图,有一直径是的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC.
(1)求AB的长;
(2)用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆的半径.
22.如图所示,在 Rt△ABC中,∠C=90°,AC=4 ,BC=3 .求以直角边所在直线为轴,把△ABC 旋转一周得到的圆锥的侧面积.
23.如图所示,一只纺锤可近似地看成是由两个圆锥拼合而成的,AB=18,AD=9,r=3.
(1)求纺锤的全面积S(结果保留π).
(2)一只蚂蚁从点C出发绕这只纺锤爬一圈回到原地,求蚂蚁爬过的最短路线长.
答案部分
1.C
2.C
3.C
4.B
5.C
6.B
7.D
8.D
9.A
10.A
11.2
12.120°
13.π;
14.15
15.
16.20π
17.
18.(1)解:该几何体为一个圆锥.
(2)解:由(1)可得:该几何题为圆锥,
底面圆半径r=12,高为6,
∴侧面母线长
∴
19.(1)解:∵在等腰三角形ABC中,∠BAC=120°,
∴∠B=30°.
∵AD是∠BAC的平分线, AD=6,
∴AD⊥BC,BD=CD,
∴,
∴,
∴由及线段FC,CB,BE围成图形(图中阴影部分)的面积为:
S△ABC-S扇形EAF==.
(2)解:设圆锥的底面半径为r,
根据题意得,
解得r=2,
则这个圆锥的高h=
20.解:在△SAB中,SA=SB,∠ASB=120°
∵SO⊥AB
∴O是AB的中点。
∴∠ASO=∠BSO=60°.
在Rt△ASO中,OA=27m.
∴tan∠ASO=tan60°=
∴SO=≈15.6m.
答:光源离地面的垂直高度SO为15.6m.
21.(1)解:连接BC,如图
∵,
∴BC为⊙O的直径,其,
∴;
(2)解:设所得圆锥的底面圆的半径为r,根据题意得,
解得:.
22.解:∵∠C=90°,AC=4 ,BC=3,∴AB=5
若以直角边AC所在直线为轴,则所得圆锥侧面积为π·BC·AB=15π
若以直角边BC所在直线为轴,则所得圆锥侧面积为π·AC·AB=20π
23.(1)解:设右侧圆锥的侧面积为S1,左侧圆锥的侧面积为S2,
则S=S1+S2=3×9×π+3×18×π=27π+54π=81π.
(2)解:设右侧圆锥的侧面展开图扇形的圆心角为θ1,
则θ1=×360°=120°.
如图,
把右侧圆锥沿母线CD展开成平面图形,连结CC',过点D作DE⊥CC',垂足为E.则由垂径定理,可知CE=C'E,∠CDE=∠C'DE=60°,
∴CC'=2CE=2CD·sin60°=2×9×=
若经过左边,同理可得最短路线长为18.
<9×=9×2=18,
∴蚂蚁爬过的最短路线长为.
一、单选题
1.某盏路灯照射的空间可以看成如图所示的圆锥,它的高,底面半径,则圆锥的侧面积为( )
A. B. C. D.
2.一个圆锥的底面半径的长为3,母线的长为15,则侧面展开图的面积是( )
A. B. C. D.
3.如图,已知圆锥侧面展开图的扇形面积为,扇形的弧长为,则圆锥的高是( )
A. B. C. D.
4.如图,在△ABC中,∠C =90°,AC>BC,若以AC为底面圆的半径,BC为高的圆锥的侧面积为S1,若以BC为底面圆的半径,AC为高的圆锥的侧面积为S2 ,则( )
A.S1 =S2 B.S1 >S2
C.S1 <S2 D.S1 ,S2的大小大小不能确定
5.如图,圆锥底面圆半径为7cm,高为24cm,则它侧面展开图的面积是( )
A. cm2 B. cm2 C.175πcm2 D.350πcm2
6.已知圆锥的底面半径为3cm,母线长为6cm,则圆锥的侧面积是( )
A.18cm2 B. C.27cm2 D.
7.如图,将半径为2的圆形纸片,沿半径OA、OB将其裁成1:3两个部分,用所得扇形围成圆锥的侧面,则圆锥的底面半径为( )
A. B.1 C.1或3 D. 或
8.在纸上剪下一个圆形和一个扇形纸片,使之恰好能够围成一个圆锥模型,若圆的半径为r,扇形的半径为R,扇形的圆心角等于120°(如图),则r与R之间的关系是( )
A.R=2r B.R= r C.R=3r D.R=4r
9.如图,是一个圆锥形纸杯的侧面展开图,已知圆锥底面半径为5cm,母线长为15cm,那么纸杯的侧面积为( )
A.75πcm2 B.150πcm2 C. D.
10.如图,在矩形中,以点A为圆心,以长为半径画弧交于点E,将扇形剪下来做成圆锥,若,则该圆锥底面半径为( )
A. B. C.1 D.2
二、填空题
11.一圆锥的母线长为6cm,它的侧面展开图的圆心角为120°,则这个圆锥的底面半径r= cm.
12.某中学开展劳动实习,学生到教具加工厂制作圆锥,他们制作的圆锥,母线长为30cm,底面圆的半径为10 cm,这种圆锥的侧面展开图的圆心角度数是 .
13.如图,在半径为 的圆形纸片中,剪一个圆心角为90°的最大扇形(阴影部分),则这个扇形的面积为 ;若将此扇形围成一个无底的圆锥(不计接头),则圆锥底面半径为 。
14.如图,从一张腰长为,底角为的等腰三角形铁皮中剪出一个最大的扇形,用此剪下的扇形铁皮围成一个圆盘的侧面(不计损耗),则该圆锥的底面半径为 cm.
15.如图(1),在正方形铁皮上剪下一个圆形和扇形,使之恰好围成如图(2)所示的一个圆锥模型,则圆的半径r与扇形的半径R之间的关系为 .
16.在中,,,,以一条直角边所在直线为轴,把旋转1周,得到圆锥,则该圆锥的侧面积最大值为 .
三、解答题
17.如图,圆锥侧面展开得到扇形,此扇形的半径,圆心角,求此圆锥的高的长.
18.下图是一个几何体的三视图.
(1)说出这个几何体的名称.
(2)请根据图中尺寸(单位:cm)求该几何体的全面积(结果保留π).
19.如图1,在等腰三角形ABC中,∠BAC=120°,AD是∠BAC的平分线,且AD=6,以点A为圆心,AD的长为半径画,交AB于点E,交AC于点F.
(1)求由及线段FC,CB,BE围成图形(图1中阴影部分)的面积(结果保留π).
(2)如图2,将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
20.如图所示,在半径为27m的广场中央,点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°,求光源离地面的垂直高度SO.(精确到0.1m;
=1. 414, =1.732, =2.236,以上数据供参考)
21.如图,有一直径是的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC.
(1)求AB的长;
(2)用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆的半径.
22.如图所示,在 Rt△ABC中,∠C=90°,AC=4 ,BC=3 .求以直角边所在直线为轴,把△ABC 旋转一周得到的圆锥的侧面积.
23.如图所示,一只纺锤可近似地看成是由两个圆锥拼合而成的,AB=18,AD=9,r=3.
(1)求纺锤的全面积S(结果保留π).
(2)一只蚂蚁从点C出发绕这只纺锤爬一圈回到原地,求蚂蚁爬过的最短路线长.
答案部分
1.C
2.C
3.C
4.B
5.C
6.B
7.D
8.D
9.A
10.A
11.2
12.120°
13.π;
14.15
15.
16.20π
17.
18.(1)解:该几何体为一个圆锥.
(2)解:由(1)可得:该几何题为圆锥,
底面圆半径r=12,高为6,
∴侧面母线长
∴
19.(1)解:∵在等腰三角形ABC中,∠BAC=120°,
∴∠B=30°.
∵AD是∠BAC的平分线, AD=6,
∴AD⊥BC,BD=CD,
∴,
∴,
∴由及线段FC,CB,BE围成图形(图中阴影部分)的面积为:
S△ABC-S扇形EAF==.
(2)解:设圆锥的底面半径为r,
根据题意得,
解得r=2,
则这个圆锥的高h=
20.解:在△SAB中,SA=SB,∠ASB=120°
∵SO⊥AB
∴O是AB的中点。
∴∠ASO=∠BSO=60°.
在Rt△ASO中,OA=27m.
∴tan∠ASO=tan60°=
∴SO=≈15.6m.
答:光源离地面的垂直高度SO为15.6m.
21.(1)解:连接BC,如图
∵,
∴BC为⊙O的直径,其,
∴;
(2)解:设所得圆锥的底面圆的半径为r,根据题意得,
解得:.
22.解:∵∠C=90°,AC=4 ,BC=3,∴AB=5
若以直角边AC所在直线为轴,则所得圆锥侧面积为π·BC·AB=15π
若以直角边BC所在直线为轴,则所得圆锥侧面积为π·AC·AB=20π
23.(1)解:设右侧圆锥的侧面积为S1,左侧圆锥的侧面积为S2,
则S=S1+S2=3×9×π+3×18×π=27π+54π=81π.
(2)解:设右侧圆锥的侧面展开图扇形的圆心角为θ1,
则θ1=×360°=120°.
如图,
把右侧圆锥沿母线CD展开成平面图形,连结CC',过点D作DE⊥CC',垂足为E.则由垂径定理,可知CE=C'E,∠CDE=∠C'DE=60°,
∴CC'=2CE=2CD·sin60°=2×9×=
若经过左边,同理可得最短路线长为18.
<9×=9×2=18,
∴蚂蚁爬过的最短路线长为.
同课章节目录
