数学八年级下人教新课标19.1函数(第4课时)函数的三种表示方法 课件
文档属性
| 名称 | 数学八年级下人教新课标19.1函数(第4课时)函数的三种表示方法 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 476.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-24 16:48:24 | ||
图片预览





文档简介
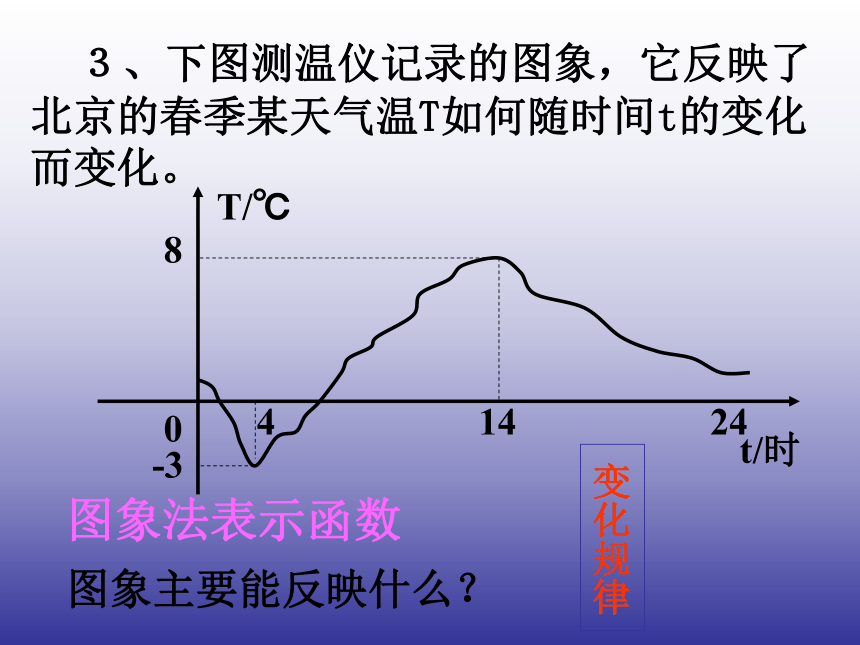
课件12张PPT。人教版八年级(下册)第十九章一次函数函数的三种表示方法(第4课时)19.1函数引 入 1、 汽车以60千米/时的速度匀速行驶,行驶里程为 s 千米,行驶时间为t 小时,写出s与t的函数解析式。S = 60t解析法表示函数解析式主要能反映数量关系列表法表示函数表格主要能反映对应关系 2、 下表是某种股票一周内周一至周五的收盘价。 12 12.5 12.9 12.45 12.75 3、下图测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。41424t/时8T/℃0图象法表示函数图象主要能反映什么?-3 变化规律表示函数关系的方法:1、解析法:准确地反映了函数与自变量之间的数量关系。2、列表法:具体地反映了函数与自变量的数值对应关系。3、图象法:直观地反映了函数随自变量的变化而变化的规律。归纳观察与思考:
观察函数的图象要注意一些什么事项呢? (1)弄清横、纵坐标表示的意义;(2)自变量的取值范围;(3)图象中函数随着自变量变化的规律。1、画出函数 y = x + 0.5 的图象1、列表解:2、描点3、连线回 顾请画出函数y= x+0.5的图象(-1, -0.5)BACD(0, 0.5)(1, 1.5)(2, 2.5)y= x+0.5如何判断一点是否在某个函数的图象上?.课堂归纳(一):如何判断一点是否在某个函数的图象上? 若一个点在某个函数图象上,那么这一点的横、纵坐标一定满足这个函数的解析式,反之则不在。
.课堂练习(一):1、下列各点中,在函数y= 图象上的是( )
A、(—2,—4) B、(4,4) C、(—2,4) D、(4,2)2、点A(1,m)在函数y=2x的图象上,则点的坐标是( )
A、(1,) B、(1,2) C、(1,1) D、(2,1)DB3.下列四个点中在函数y=2x—3的图象上有( )个。
(1,2) , (3,3) , (—1, —1), (1.5,0) A.1 B.2 C.3 D.4B某水库的水位在最近的5小时持续上涨,下表记录了这五小时的水位高度。(1)由记录表推出这5小时中水位高度y(单位:千米)随时间t(单位:时)变化的函数解析式,并画出函数图象;
(2)按估计按这种上涨规律还会持续上涨2小时,预测再过2小时水位高度将达到多少米。
课本P81练习第1题、第2题、第3题。
观察函数的图象要注意一些什么事项呢? (1)弄清横、纵坐标表示的意义;(2)自变量的取值范围;(3)图象中函数随着自变量变化的规律。1、画出函数 y = x + 0.5 的图象1、列表解:2、描点3、连线回 顾请画出函数y= x+0.5的图象(-1, -0.5)BACD(0, 0.5)(1, 1.5)(2, 2.5)y= x+0.5如何判断一点是否在某个函数的图象上?.课堂归纳(一):如何判断一点是否在某个函数的图象上? 若一个点在某个函数图象上,那么这一点的横、纵坐标一定满足这个函数的解析式,反之则不在。
.课堂练习(一):1、下列各点中,在函数y= 图象上的是( )
A、(—2,—4) B、(4,4) C、(—2,4) D、(4,2)2、点A(1,m)在函数y=2x的图象上,则点的坐标是( )
A、(1,) B、(1,2) C、(1,1) D、(2,1)DB3.下列四个点中在函数y=2x—3的图象上有( )个。
(1,2) , (3,3) , (—1, —1), (1.5,0) A.1 B.2 C.3 D.4B某水库的水位在最近的5小时持续上涨,下表记录了这五小时的水位高度。(1)由记录表推出这5小时中水位高度y(单位:千米)随时间t(单位:时)变化的函数解析式,并画出函数图象;
(2)按估计按这种上涨规律还会持续上涨2小时,预测再过2小时水位高度将达到多少米。
课本P81练习第1题、第2题、第3题。
