数学八年级下人教新课标19.2一次函数 (第5课时)一次函数与一元一次不等式 课件
文档属性
| 名称 | 数学八年级下人教新课标19.2一次函数 (第5课时)一次函数与一元一次不等式 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 372.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-24 16:56:16 | ||
图片预览


文档简介
课件11张PPT。人教版八年级(下册)第十九章一次函数一次函数与一元一次不等式19.2.3一次函数与方程、不等式练一练:
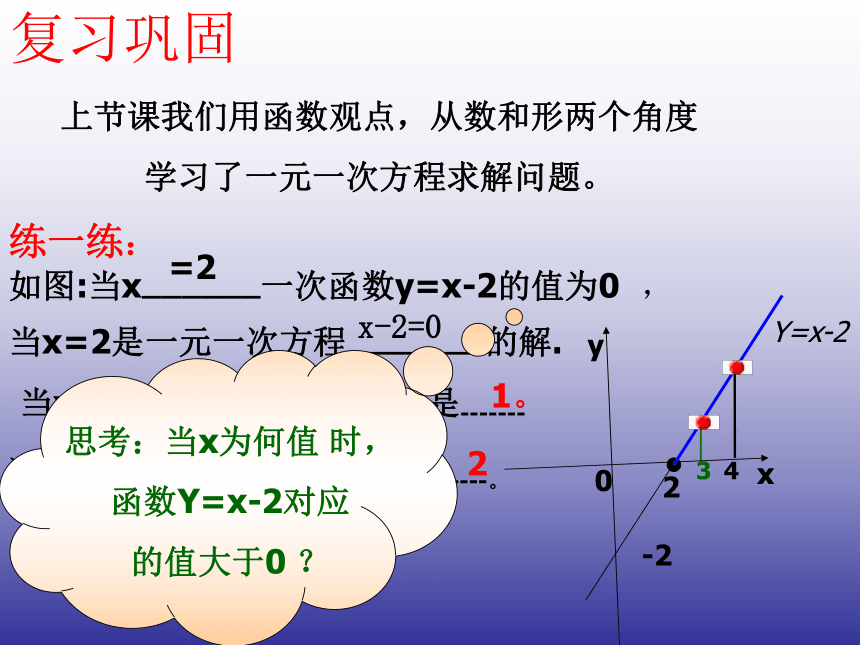
如图:当x——————一次函数y=x-2的值为0 ,复习巩固当x=2是一元一次方程———————的解.=2x-2=034当x=3时,函数y=x-2的值是-------1。当x=4,函数y=x-2的值是--------。2思考:当x为何值 时,
函数Y=x-2对应
的值大于0 ?
上节课我们用函数观点,从数和形两个角度
学习了一元一次方程求解问题。
探究:解:(1)把5x+6>3x+10转化为2x-4>0,解得x >2。
⑵就是要解不等式2x-4>0,解得x >2。
当x >2时,函数y=2x-4的值大于0。(1)解不等式:5x+6>3x+10。
(2)当x为何值时,函数y=2x-4的值大于0?议一议:在上面的问题解
决过程中,你能发现它们
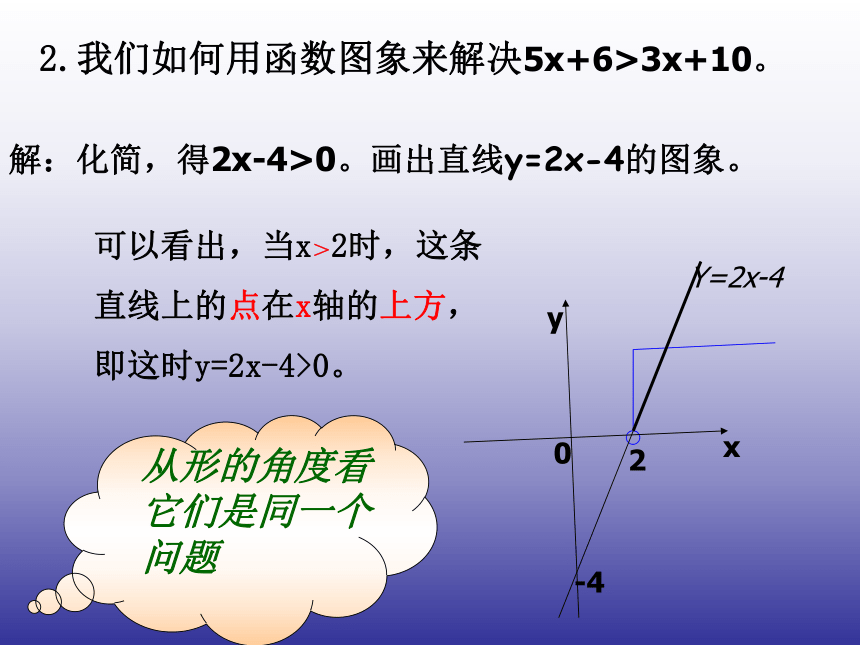
之间有什么关系吗?从数的角度看它们是同一个问题2.我们如何用函数图象来解决5x+6>3x+10。
解:化简,得2x-4>0。画出直线y=2x-4的图象。可以看出,当x>2时,这条
直线上的点在x轴的上方,
即这时y=2x-4>0。
从形的角度看它们是同一个问题
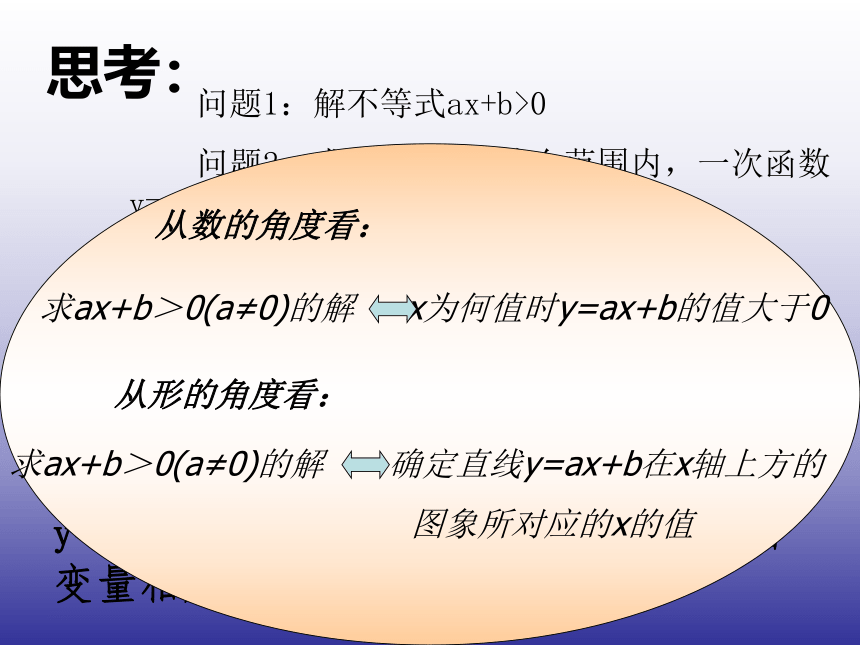
思考: 问题1:解不等式ax+b>0
问题2:求自变量x在什么范围内,一次函数 y=ax+b的值大于0
上面两个问题有什么关系? 从实践中得出,由于任何一元一次不等式都可以转化为ax+b>0或ax+b<0(a,b为常数,a≠0)的形式,所以解一元一次不等式可以看作:当一次函数y=ax+b的值大于0(或小于0)时,求自变量相应的取值范围。从数的角度看:从形的角度看: 根据下列一次函数的图象,你能求出哪些不等式的解集?并直接写出相应的不等式的解集。3x+6>0 ( x>- 2)3x+6<0 ( x<- 2)
3x+6≥0 ( x ≥- 2)3x+6≤0 ( x ≤ - 2)
试一试可以看出,当x<2时,这条直线上的点在x轴的下方,解:化简,得3x-6<0。画出直线y=3x-6,即这时y=3x-6<0,所以不等式的解集为x<2。
例1.用画函数图象的方法解不等式 5x+4<2x+10.
尝试:
例2:已知函数Y1=5X+4,Y2=2X+10,求当X为何值时,Y1=Y2?X为何值时,Y1Y1=5X+4上的点在直线
Y2=2X+10上相应点的下方时,
5X+4 < 2X+10,所以不等式的解集为X<2。你能有几种方法
解不等式
5x+4<2x+10-22、如图,直线L1, L2交于一点P,若y1 ≥y2 ,则( )
x ≥ 3
x ≤3
2 ≤ x ≤ 3
x ≤ 41、已知函数Y=3X+8,当X————————,函数
的值等于0。当X————————,函数的值大于0。当X———————— ,函数的值不大于2。= ≤- 2>B做一做3.利用函数图象解不等式:3x-4<x+2(用两种方法)解法1:化简不等式得2x-6<0,画出函数y=2x-6的图象,当x<3时y=2x-6<0,所以不等式的解集为x<3。解法2:画出函数y=3x-4和函数y=x+2的图象,交点横坐标为3,当x<3时,对于同一个x,直线y=3x-4上的点在直线y=x+2上相应点的下方,这表示3x-4<x+2,所以不等式的解集为x < 3。五.小结一下 1.这节课我们学到了哪些知识?
2.我们是用哪些方法获得这些知识的?
3.你觉得还有什么问题需要继续讨论吗?
小 结
如图:当x——————一次函数y=x-2的值为0 ,复习巩固当x=2是一元一次方程———————的解.=2x-2=034当x=3时,函数y=x-2的值是-------1。当x=4,函数y=x-2的值是--------。2思考:当x为何值 时,
函数Y=x-2对应
的值大于0 ?
上节课我们用函数观点,从数和形两个角度
学习了一元一次方程求解问题。
探究:解:(1)把5x+6>3x+10转化为2x-4>0,解得x >2。
⑵就是要解不等式2x-4>0,解得x >2。
当x >2时,函数y=2x-4的值大于0。(1)解不等式:5x+6>3x+10。
(2)当x为何值时,函数y=2x-4的值大于0?议一议:在上面的问题解
决过程中,你能发现它们
之间有什么关系吗?从数的角度看它们是同一个问题2.我们如何用函数图象来解决5x+6>3x+10。
解:化简,得2x-4>0。画出直线y=2x-4的图象。可以看出,当x>2时,这条
直线上的点在x轴的上方,
即这时y=2x-4>0。
从形的角度看它们是同一个问题
思考: 问题1:解不等式ax+b>0
问题2:求自变量x在什么范围内,一次函数 y=ax+b的值大于0
上面两个问题有什么关系? 从实践中得出,由于任何一元一次不等式都可以转化为ax+b>0或ax+b<0(a,b为常数,a≠0)的形式,所以解一元一次不等式可以看作:当一次函数y=ax+b的值大于0(或小于0)时,求自变量相应的取值范围。从数的角度看:从形的角度看: 根据下列一次函数的图象,你能求出哪些不等式的解集?并直接写出相应的不等式的解集。3x+6>0 ( x>- 2)3x+6<0 ( x<- 2)
3x+6≥0 ( x ≥- 2)3x+6≤0 ( x ≤ - 2)
试一试可以看出,当x<2时,这条直线上的点在x轴的下方,解:化简,得3x-6<0。画出直线y=3x-6,即这时y=3x-6<0,所以不等式的解集为x<2。
例1.用画函数图象的方法解不等式 5x+4<2x+10.
尝试:
例2:已知函数Y1=5X+4,Y2=2X+10,求当X为何值时,Y1=Y2?X为何值时,Y1
Y2=2X+10上相应点的下方时,
5X+4 < 2X+10,所以不等式的解集为X<2。你能有几种方法
解不等式
5x+4<2x+10-22、如图,直线L1, L2交于一点P,若y1 ≥y2 ,则( )
x ≥ 3
x ≤3
2 ≤ x ≤ 3
x ≤ 41、已知函数Y=3X+8,当X————————,函数
的值等于0。当X————————,函数的值大于0。当X———————— ,函数的值不大于2。= ≤- 2>B做一做3.利用函数图象解不等式:3x-4<x+2(用两种方法)解法1:化简不等式得2x-6<0,画出函数y=2x-6的图象,当x<3时y=2x-6<0,所以不等式的解集为x<3。解法2:画出函数y=3x-4和函数y=x+2的图象,交点横坐标为3,当x<3时,对于同一个x,直线y=3x-4上的点在直线y=x+2上相应点的下方,这表示3x-4<x+2,所以不等式的解集为x < 3。五.小结一下 1.这节课我们学到了哪些知识?
2.我们是用哪些方法获得这些知识的?
3.你觉得还有什么问题需要继续讨论吗?
小 结
