2024-2025学年四年级数学上册寒假巩固练习(人教版)第5练-平行四边形和梯形(含解析)
文档属性
| 名称 | 2024-2025学年四年级数学上册寒假巩固练习(人教版)第5练-平行四边形和梯形(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 791.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-21 14:07:43 | ||
图片预览



文档简介
2024-2025学年四年级数学上册寒假巩固练习(人教版)
第5练-平行四边形和梯形
一、单选题
1.下列说法中正确的是( )。
A.两个锐角的和一定比直角大 B.长方形相邻的两条边互相垂直
C.不相交的两条直线叫平行线 D.一条直线长5厘米
2.下列关系图中,表示正确的是( )。
A. B.
C. D.
3. 一个四边形被墨迹遮住了一部分,请你根据露出的部分推测它( )
A.一定是平行四边形
B.一定是梯形
C.可能是平行四边形,也可能是梯形
4.下面的汉字中,( )既有互相垂直的线段,又有互相平行的线段。
A. B. C.
5.下面图形之间的关系表述最合理的是( )。
A.
B.
C.
D.
6.如下图把一张等腰梯形纸剪一刀后得到了两个新图形,这个新图形不可能是( )。
A.两个平行四边形 B.两个梯形
C.一个三角形和一个平行四边形 D.两个三角形
7.下列说法中,正确的有( ) 句。
①如果▲×●=20,则(▲×4)×(●÷4) =80。
②算式17÷4和1700÷400,它们的商都是4,余数都是1。
③长方形是特殊的平行四边形,梯形也是特殊的平行四边形。
④四根分别长5cm,5cm,4cm,4cm的小棒能搭成很多不同形状的平行四边形。
A.1 B.2 C.3 D.4
8.如图藏在云朵后面的图形不可能是( )。
A.锐角三角形 B.钝角三角形 C.梯形 D.平行四边形
二、填空题
9.两条平行线之间可以画 条垂线段,垂线段的长度 (填“相等”或“不相等”)。
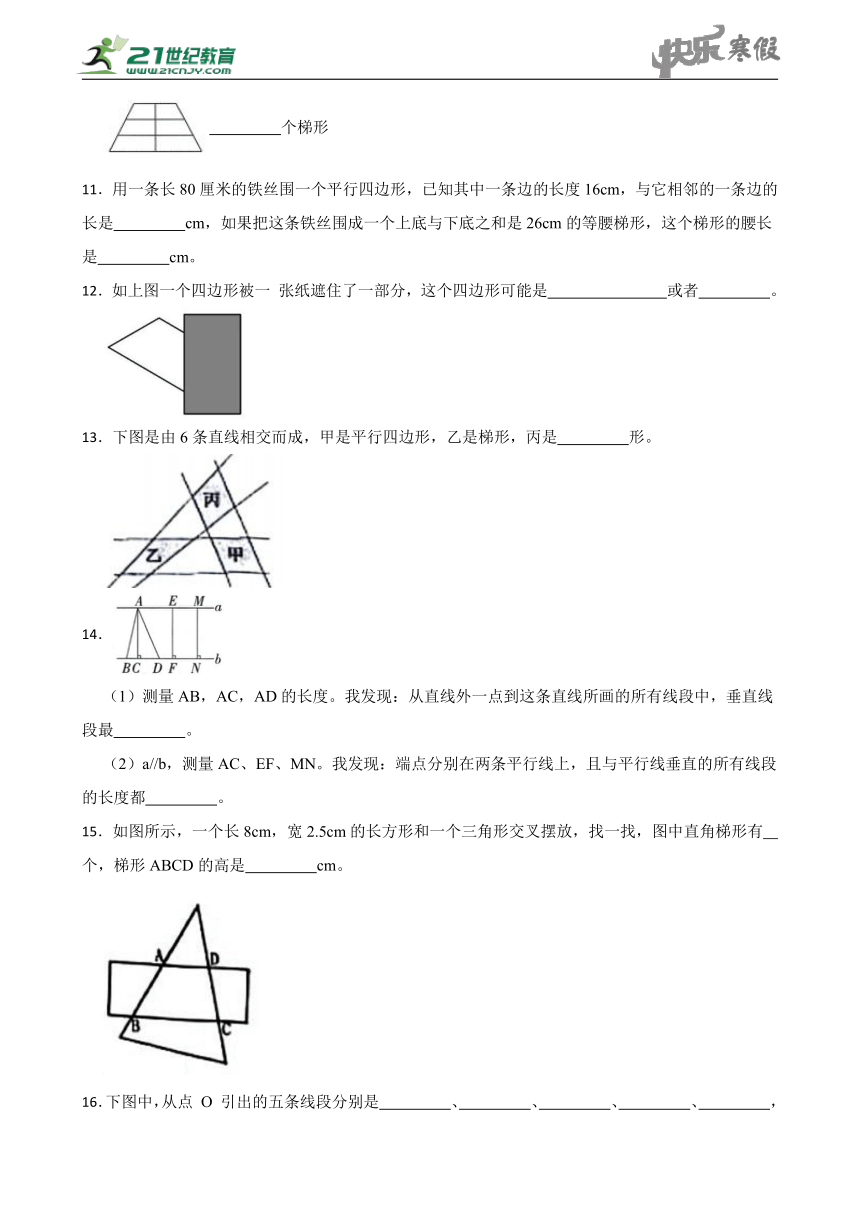
10.下图中有几个平行四边形? 几个梯形?
个平行四边形
个梯形
11.用一条长80厘米的铁丝围一个平行四边形,已知其中一条边的长度16cm,与它相邻的一条边的长是 cm,如果把这条铁丝围成一个上底与下底之和是26cm的等腰梯形,这个梯形的腰长是 cm。
12.如上图一个四边形被一 张纸遮住了一部分,这个四边形可能是 或者 。
13.下图是由6条直线相交而成,甲是平行四边形,乙是梯形,丙是 形。
14.
(1)测量AB,AC,AD的长度。我发现:从直线外一点到这条直线所画的所有线段中,垂直线段最 。
(2)a//b,测量AC、EF、MN。我发现:端点分别在两条平行线上,且与平行线垂直的所有线段的长度都 。
15.如图所示,一个长8cm,宽2.5cm的长方形和一个三角形交叉摆放,找一找,图中直角梯形有 个,梯形ABCD的高是 cm。
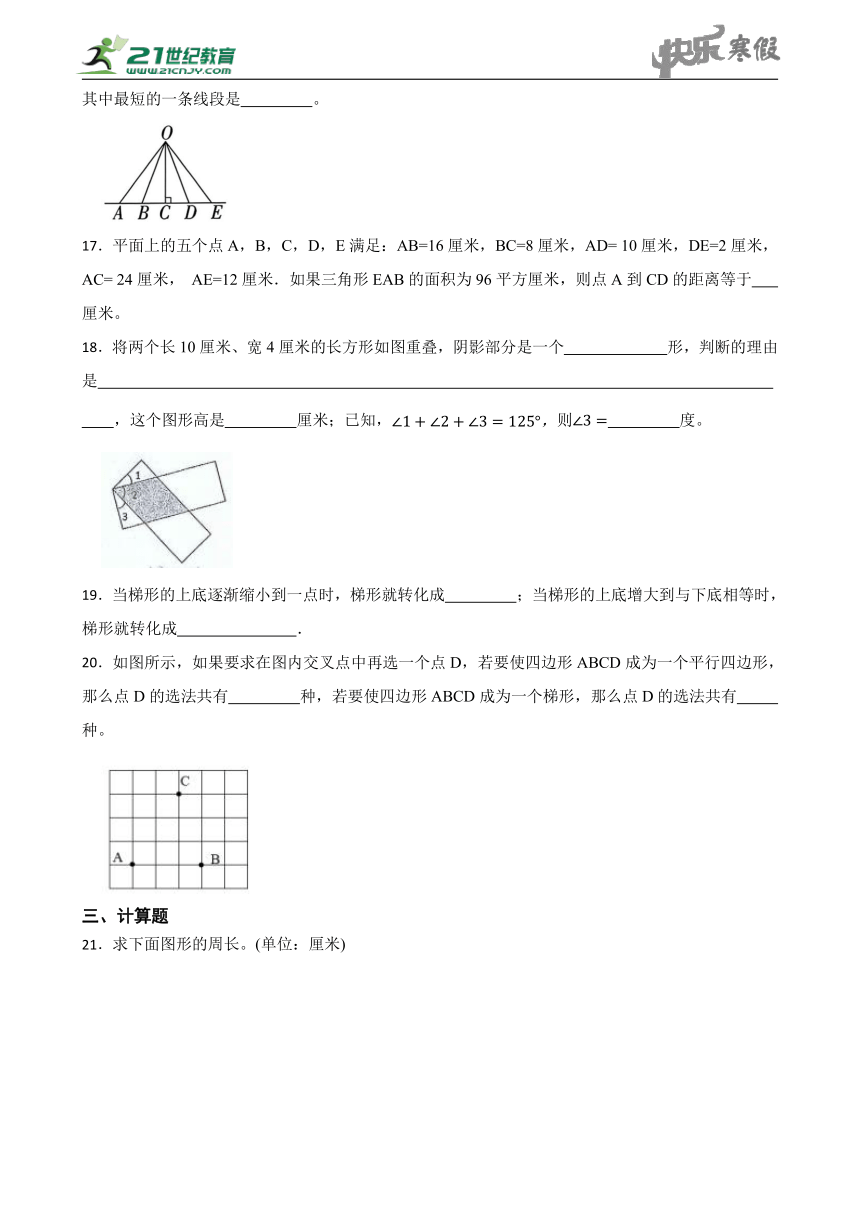
16.下图中,从点 O 引出的五条线段分别是 、 、 、 、 ,其中最短的一条线段是 。
17.平面上的五个点A,B,C,D,E满足:AB=16厘米,BC=8厘米,AD= 10厘米,DE=2厘米,AC= 24厘米, AE=12厘米.如果三角形EAB的面积为96平方厘米,则点A到CD的距离等于 厘米。
18.将两个长10厘米、宽4厘米的长方形如图重叠,阴影部分是一个 形,判断的理由是 ,这个图形高是 厘米;已知,则 度。
19.当梯形的上底逐渐缩小到一点时,梯形就转化成 ;当梯形的上底增大到与下底相等时,梯形就转化成 .
20.如图所示,如果要求在图内交叉点中再选一个点D,若要使四边形ABCD成为一个平行四边形,那么点D的选法共有 种,若要使四边形ABCD成为一个梯形,那么点D的选法共有 种。
三、计算题
21.求下面图形的周长。(单位:厘米)
四、作图题
22.淘气在泳池里游泳,现在A处。
23.根据学校部分区域的平面示意图填一填,画一画
(1)测量图上线段AB= 厘米,∠1= °。
(2)过操场B修一条与甬道AC平行的人行道,请你在图上画出来。
(3)从自来水主管道AB向喷泉C铺设一条水管,你认为怎样铺设最合理?请在图中画出来。
(4)学校计划以学校门口A为起点,向东南方向修一条车道AD,使∠CAD=60°,请你在图上画出车道AD的位置。
五、解决问题
24. 用12分米长的一根铁丝围成一个平行四边形,这个平行四边形的一条边长4分米,拉动平行四边形使其变成长方形,长方形的面积是多少平方分米?
25.有一个平行四边形的刺绣挂件,相邻两边的长度分别是45厘米和40厘米,想把这个刺绣挂件用框裱起来,需要的框的周长是多少?
26.下图是由a、b、c、d、e、f六条直线相交而成的。已知甲是平行四边形,乙是梯形,那么丙是什么图形 请说明你的判断理由。
27. 聪聪和明明相约周末一起去郊游,他们1.2小时走了 2.88 千米,离目的地还有3.6千米,按照这样的速度,他们还要走多长时间?
28. 一个长方形框架的周长是48厘米,长是15厘米,把它拉成一个平行四边形后,这个平行四边形的四条边分别是多少厘米?
29.一个梯形的下底的长度是上底的4倍,如果将这个梯形的上底延长30厘米,这个梯形就变成了一个平行四边形。这个梯形的上底和下底分别有多长
答案解析部分
1.B
解:A 如果两个锐角是20°、30°,则两个锐角的和是50°,还是锐角,原题说法错误;
B 长方形相邻的两条边互相垂直 ,原题说法正确;
C 不相交的两条直线互相平行,原题说法错误;
D 直线没有端点,没有固定长度,原题说法错误;
故答案为:B。
两个锐角和可能是锐角,也可能是直角,也可能是钝角;长方形的四个角都是直角,相邻的两条边互相垂直;在同一平面内,不相交的两条直线互相平行;直线是向两边无限延长的。
2.C
解:A项:平行四边形不包括梯形,原题干说法错误;
B项:四边形不包括三角形,原题干说法错误;
C项:直角梯形是梯形的一种,原题干说法正确;
D项:在同一平面内,垂直是相交的一种。
故答案为:C。
有一个角是直角的梯形是直角梯形,直角梯形是梯形的一种。
3.C
解:因为露出的三条边中有一组对边平行,另一组对边或者平行或者不平行,所以这个四边形可能是平行四边形,也可能是梯形。
故答案为:C。
两组对边分别平行的四边形是平行四边形;只有一组对边平行的四边形是梯形。
4.C
选项A,只有互相平行的线段;
选项B,只有互相垂直的线段;
选项C, 既有互相垂直的线段,又有互相平行的线段。
故答案为:C。
根据垂直和平行的性质:在同一平面内相交成直角的两条直线叫做互相垂直,不相交的两条直线叫做平行线,据此判断即可。
5.C
解:A:平行四边形不包括梯形,此选项错误;
B:梯形不包括长方形和正方形,此选项错误;
C:此选项正确;
D:梯形不包括平行四边形,此选项错误。
故答案为:C。
梯形、平行四边形、长方形和正方形都是四边形。正方形是特殊的长方形,长方形和正方形都是特殊的平行四边形。梯形是只有一组对边平行的四边形。平行四边形、长方形、正方形都是两组对边都平行且相等的四边形。
6.A
解:如图,不可能是两个平行四边形。
故答案为:A。
把一张等腰梯形纸剪一刀,会得到两个梯形,一个三角形和一个平行四边形,或者两个三角形,不可能是两个平行四边形。
7.A
①如果▲×●=20,则(▲×4)×(●÷4) =20,原题说法错误;
②算式17÷4和1700÷400,它们的商都是4,余数不同,17÷4的余数是1,1700÷400的余数是100,原题说法错误;
③长方形是特殊的平行四边形,梯形不是平行四边形,原题说法错误;
④四边形容易变形,四根分别长5cm,5cm,4cm,4cm的小棒能搭成很多不同形状的平行四边形,如长方形、不同的平行四边形,原题说法正确。
故答案为:A。
积的变化规律:一个因数扩大a倍,另一个因数缩小a倍,积不变;
计算被除数和除数末尾有0的除法,同时缩小相同的倍数,商不变,余数会缩小相同的倍数;
长方形、正方形是特殊的平行四边形,梯形不是平行四边形;
平行四边形容易变形,四条边的长度固定,但是它的形状可以发生变化。
8.A
解:露出的是一个钝角,所以后面的图形不可能是锐角三角形。
故答案为:A。
钝角三角形、梯形、平行四边形都有钝角,锐角三角形三个角都是锐角。
9.无数;相等
解:两条平行线之间可以画无数条垂线段,垂线段的长度相等。
故答案为:无数;相等。
两条平行线间垂线段的长度就是两条平行线之间的距离,两条平行线间的距离处处相等。
10.6;18
解:3+2+1=6(个)
6+6+6=18(个)。
故答案为:6;18。
有两组对边平行且相等的四边形是平行四边形,有一组对边平行的四边形是梯形。通过观察可知,第一个图形:单个的平行四边形有3个,由两个平行四边形组成的平行四边形有2个,由三个平行四边形组成的平行四边形有1个,因此共6个平行四边形。第二个图形:单个的梯形有6个,由两个梯形组成的梯形有7个,由三个梯形组成的梯形有2个,由四个梯形组成的梯形有2个,由六个梯形组成的梯形有1个,共18个。
11.24;27
解:80÷2-16=24(cm),所以与它相邻的一条边的长是24cm;(80-26)÷2=27(cm),所以这个梯形的腰长是27cm。
故答案为:24;27。
平行四边形相邻两边之和=铁丝的长度÷2-其中一条边的长度;
等腰梯形的腰=(铁丝的长度-上下底之和)÷2。
12.平行四边形;梯形
解:如果遮住的另一条边与对边平行,则平行四边形;如果遮住的另一条边不与对边平行,则是梯形。
故答案为:平行四边形;梯形。
两组对边分别平行的四边形叫做平行四边形;
只有一组对边平行的四边形叫做梯形。
13.梯
解:丙中有两条边互相平行,另外两条边不平行,所以丙是梯形。
故答案为:梯。
乙是梯形,甲是平行四边形,所以乙和甲所在的两条直线平行,乙和丙所在的两条直线不平行,丙和甲所在的两条直线平行。所以丙是梯形。
14.(1)短
(2)相等
解:(1)从直线外一点到这条直线所画的所有线段中,垂直线段最短;
(2)端点分别在两条平行线上,且与平行线垂直的所有线段的长度都相等。
故答案为:(1)短;(2)相等。
(1)从直线外一点到这条直线所画的所有线段中,垂直线段最短;
(2)两条平行线间的距离相等。
15.4;2.5
解:直角梯形有4个,梯形ABCD的高是2.5cm。
故答案为:4;2.5。
直角梯形:有两个直角的梯形。所以如图 、 、 、 一共4个直角梯形;
梯形的高:上底与下底之间的距离就是梯形的高。如图 ,看图可知梯形的高与长方形的宽一样长,所以梯形的高是2.5cm。
16.OA;OB;OC;OD;OE;OC
解:从点 O 引出的五条线段分别是:OA、OB、OC、OD、OE,其中最短的一条线段是OC。
故答案为:OA;OB;OC;OD;OE;OC。
此题主要考查了点到直线的距离,从直线外一点到这条直线所画的垂直线段最短,这条线段叫点到直线的距离。
17.
解:按照题意,可以得知,ABC是在一条直线上,否则形不成AC=12厘米,同样,ADE也在一条直线上.
因为:△EAB面积是24平方厘米,而只有角A是90度直角时,其面积才是:AB×(AD+DE)÷2=8×6÷2=24,
所以,角A是直角.
A是直角,则△CAD也是直角三角形,
根据勾股定理CD×CD=AD2+AC2,
解得CD=13厘米.
设:点A到CD的距离为x(也就是CD边上的高)列出方程:
解得,
故答案为:
通过应用勾股定理确定三角形CAD的形状。确定三角形CAD形状后,即可计算出CD的长度。通过三角形CAD的面积除以CD的长度即可计算点A到直线CD的距离
18.平行四边;长方形的对边互相平行,两个长方形如图重叠,组成的图形的对边分别平行,是一个平行四边形;4;35
解:阴影部分是一个平行四边形,理由是长方形的对边互相平行,两个长方形如图重叠,组成的图形的对边分别平行,是一个平行四边形,这个图形的高是4厘米;
因为∠1+∠2=90°,∠2+∠3=90°,又知∠1+∠2+∠3=125°,所以∠3=125°-(∠1+∠2)=125°-90°=35°。
故答案为:平行四边;长方形的对边互相平行,两个长方形如图重叠,组成的图形的对边分别平行,是一个平行四边形;4;35。
长方形的特征:两组对边互相平行且相等,四个角都是直角,两个长方形如图重叠,组成的图形是一个平行四边形,因为长方形的对边互相平行,两个长方形如图重叠,组成的图形的对边分别平行,是一个平行四边形;平行四边形的高是长方形的宽;
观察图可知,∠1+∠2=90°,∠2+∠3=90°,又知∠1+∠2+∠3=125°,代入即可求出∠3的度数。
19.三角形;平行四边形
解:由图可知:当梯形的上底逐渐缩小到一点时,梯形就转化成三角形;当梯形的上底增大到与下底相等时,梯形就转化成平行四边形;
故答案为:三角形,平行四边形.
此题应结合图形进行分析、解答即可.
20.2;4
解:如果要求在图内交叉点中再选一个点D,若要使四边形ABCD成为一个平行四边形,那么点D的选法共有2种,若要使四边形ABCD成为一个梯形,那么点D的选法共有4种。
故答案为:2;4。
若要使四边形ABCD成为一个平行四边形,D可以在C点左、右的3个长度的地方,那么点D的选法共有2种;若要使四边形ABCD成为一个梯形,那么点D的选法共有4种,分别在C点左、右1个、2个长度的地方。
21.(24+16)×2= 80(厘米)
22.解:图中所画的线段,就是他最快游上岸的路线,
从直线外一点到这条直线的所有线段中,垂直线段最短,它的长度叫做点到直线的距离。
23.(1)2;30
(2)解:
(3)解:
(4)解:
解:(1)测量图上线段AB=2厘米,∠1=30°。
故答案为:(1)2;30。
(1)测量线段的长度,先把0刻度线与一个顶点重合,观察另一端所指的刻度;
测量角的度数时,先把量角器的中心和角的顶点重合,把0°刻度线与角的一条边重合,然后观察另一条边所指的刻度;
(2)过直线外一点做这条直线的平行线,先把三角尺的一条直角边和这条直线重合,把直尺和另一条直角边重合,保证直尺不动,平移三角尺,直到这个点出现在第一条直角边上,然后沿着这条边画线即可;
(3)过直线外一点,做这条直线的垂线,先把三角尺的一条直角边与这条直线重合,然后平移三角尺,直到这个点出现在另一条直角边上,然后沿着这条边画线即可;
(4)用量角器画角时,先画出角的顶点和一条边,把量角器的中心和角的顶点重合,把0°刻度线和角的另一条边重合,再在量角器上找到所要画的刻度,并做上标记,最后把标记和顶点连接起来即可。
24.解:12÷2-4
=6-4
=2(分米)
4×2=8(平方分米)
答:长方形的面积是8平方分米。
根据“平行四边形的周长=邻边长之和×2”,可以求出平行四边形的两条邻边中另一条边的长度;拉动平行四边形变成长方形,两条邻边长不变,变为长方形的长和宽,根据“长方形的面积=长×宽”求解。
25.解: (45 +40)×2
=85×2
= 170(厘米)
答:需要的框的周长是170厘米。
平行四边形两条邻边的长度和×2=平行四边形的周长。
26.解:甲是平行四边形,说明a∥b,f∥e,
乙是梯形,说明d不平行c,
图形丙,左右平行,上下不平行,说明丙是梯形。
两组对边分别平行的四边形叫做平行四边形;一组对边平行而另一组对边不平行的四边形是梯形;据此解答。
27.3.6÷(2.88÷1.2)=1.5(小时)
28.解:48÷2-15
=24-15
=9(厘米)
答:这个平行四边形的四条边分别是15厘米、9厘米、15厘米、9厘米。
长方形框架的长与宽之和=长方形框架的周长÷2,所以长方形的宽=长方形的长与宽之和-长方形的长;
把长方形拉成平行四边形后,长方形的长是平行四边形的底,长方形的宽是平行四边形的腰。
29.解:30÷(4-1)
=30÷3
=10(厘米)
10×4=40(厘米)
答:这个梯形的上底是10厘米,下底是40厘米。
梯形的下底的长度是上底的4倍,可以把下底看成4份,上底看成1份,下底比上底多3份;又因为上底延长30厘米这个梯形就变成了平行四边形,平行四边形对边平行且相等,则多出的3份对应30厘米;算出每一份是的长度,也就求出了上底的长度,再乘以4即为下底的长度。
第5练-平行四边形和梯形
一、单选题
1.下列说法中正确的是( )。
A.两个锐角的和一定比直角大 B.长方形相邻的两条边互相垂直
C.不相交的两条直线叫平行线 D.一条直线长5厘米
2.下列关系图中,表示正确的是( )。
A. B.
C. D.
3. 一个四边形被墨迹遮住了一部分,请你根据露出的部分推测它( )
A.一定是平行四边形
B.一定是梯形
C.可能是平行四边形,也可能是梯形
4.下面的汉字中,( )既有互相垂直的线段,又有互相平行的线段。
A. B. C.
5.下面图形之间的关系表述最合理的是( )。
A.
B.
C.
D.
6.如下图把一张等腰梯形纸剪一刀后得到了两个新图形,这个新图形不可能是( )。
A.两个平行四边形 B.两个梯形
C.一个三角形和一个平行四边形 D.两个三角形
7.下列说法中,正确的有( ) 句。
①如果▲×●=20,则(▲×4)×(●÷4) =80。
②算式17÷4和1700÷400,它们的商都是4,余数都是1。
③长方形是特殊的平行四边形,梯形也是特殊的平行四边形。
④四根分别长5cm,5cm,4cm,4cm的小棒能搭成很多不同形状的平行四边形。
A.1 B.2 C.3 D.4
8.如图藏在云朵后面的图形不可能是( )。
A.锐角三角形 B.钝角三角形 C.梯形 D.平行四边形
二、填空题
9.两条平行线之间可以画 条垂线段,垂线段的长度 (填“相等”或“不相等”)。
10.下图中有几个平行四边形? 几个梯形?
个平行四边形
个梯形
11.用一条长80厘米的铁丝围一个平行四边形,已知其中一条边的长度16cm,与它相邻的一条边的长是 cm,如果把这条铁丝围成一个上底与下底之和是26cm的等腰梯形,这个梯形的腰长是 cm。
12.如上图一个四边形被一 张纸遮住了一部分,这个四边形可能是 或者 。
13.下图是由6条直线相交而成,甲是平行四边形,乙是梯形,丙是 形。
14.
(1)测量AB,AC,AD的长度。我发现:从直线外一点到这条直线所画的所有线段中,垂直线段最 。
(2)a//b,测量AC、EF、MN。我发现:端点分别在两条平行线上,且与平行线垂直的所有线段的长度都 。
15.如图所示,一个长8cm,宽2.5cm的长方形和一个三角形交叉摆放,找一找,图中直角梯形有 个,梯形ABCD的高是 cm。
16.下图中,从点 O 引出的五条线段分别是 、 、 、 、 ,其中最短的一条线段是 。
17.平面上的五个点A,B,C,D,E满足:AB=16厘米,BC=8厘米,AD= 10厘米,DE=2厘米,AC= 24厘米, AE=12厘米.如果三角形EAB的面积为96平方厘米,则点A到CD的距离等于 厘米。
18.将两个长10厘米、宽4厘米的长方形如图重叠,阴影部分是一个 形,判断的理由是 ,这个图形高是 厘米;已知,则 度。
19.当梯形的上底逐渐缩小到一点时,梯形就转化成 ;当梯形的上底增大到与下底相等时,梯形就转化成 .
20.如图所示,如果要求在图内交叉点中再选一个点D,若要使四边形ABCD成为一个平行四边形,那么点D的选法共有 种,若要使四边形ABCD成为一个梯形,那么点D的选法共有 种。
三、计算题
21.求下面图形的周长。(单位:厘米)
四、作图题
22.淘气在泳池里游泳,现在A处。
23.根据学校部分区域的平面示意图填一填,画一画
(1)测量图上线段AB= 厘米,∠1= °。
(2)过操场B修一条与甬道AC平行的人行道,请你在图上画出来。
(3)从自来水主管道AB向喷泉C铺设一条水管,你认为怎样铺设最合理?请在图中画出来。
(4)学校计划以学校门口A为起点,向东南方向修一条车道AD,使∠CAD=60°,请你在图上画出车道AD的位置。
五、解决问题
24. 用12分米长的一根铁丝围成一个平行四边形,这个平行四边形的一条边长4分米,拉动平行四边形使其变成长方形,长方形的面积是多少平方分米?
25.有一个平行四边形的刺绣挂件,相邻两边的长度分别是45厘米和40厘米,想把这个刺绣挂件用框裱起来,需要的框的周长是多少?
26.下图是由a、b、c、d、e、f六条直线相交而成的。已知甲是平行四边形,乙是梯形,那么丙是什么图形 请说明你的判断理由。
27. 聪聪和明明相约周末一起去郊游,他们1.2小时走了 2.88 千米,离目的地还有3.6千米,按照这样的速度,他们还要走多长时间?
28. 一个长方形框架的周长是48厘米,长是15厘米,把它拉成一个平行四边形后,这个平行四边形的四条边分别是多少厘米?
29.一个梯形的下底的长度是上底的4倍,如果将这个梯形的上底延长30厘米,这个梯形就变成了一个平行四边形。这个梯形的上底和下底分别有多长
答案解析部分
1.B
解:A 如果两个锐角是20°、30°,则两个锐角的和是50°,还是锐角,原题说法错误;
B 长方形相邻的两条边互相垂直 ,原题说法正确;
C 不相交的两条直线互相平行,原题说法错误;
D 直线没有端点,没有固定长度,原题说法错误;
故答案为:B。
两个锐角和可能是锐角,也可能是直角,也可能是钝角;长方形的四个角都是直角,相邻的两条边互相垂直;在同一平面内,不相交的两条直线互相平行;直线是向两边无限延长的。
2.C
解:A项:平行四边形不包括梯形,原题干说法错误;
B项:四边形不包括三角形,原题干说法错误;
C项:直角梯形是梯形的一种,原题干说法正确;
D项:在同一平面内,垂直是相交的一种。
故答案为:C。
有一个角是直角的梯形是直角梯形,直角梯形是梯形的一种。
3.C
解:因为露出的三条边中有一组对边平行,另一组对边或者平行或者不平行,所以这个四边形可能是平行四边形,也可能是梯形。
故答案为:C。
两组对边分别平行的四边形是平行四边形;只有一组对边平行的四边形是梯形。
4.C
选项A,只有互相平行的线段;
选项B,只有互相垂直的线段;
选项C, 既有互相垂直的线段,又有互相平行的线段。
故答案为:C。
根据垂直和平行的性质:在同一平面内相交成直角的两条直线叫做互相垂直,不相交的两条直线叫做平行线,据此判断即可。
5.C
解:A:平行四边形不包括梯形,此选项错误;
B:梯形不包括长方形和正方形,此选项错误;
C:此选项正确;
D:梯形不包括平行四边形,此选项错误。
故答案为:C。
梯形、平行四边形、长方形和正方形都是四边形。正方形是特殊的长方形,长方形和正方形都是特殊的平行四边形。梯形是只有一组对边平行的四边形。平行四边形、长方形、正方形都是两组对边都平行且相等的四边形。
6.A
解:如图,不可能是两个平行四边形。
故答案为:A。
把一张等腰梯形纸剪一刀,会得到两个梯形,一个三角形和一个平行四边形,或者两个三角形,不可能是两个平行四边形。
7.A
①如果▲×●=20,则(▲×4)×(●÷4) =20,原题说法错误;
②算式17÷4和1700÷400,它们的商都是4,余数不同,17÷4的余数是1,1700÷400的余数是100,原题说法错误;
③长方形是特殊的平行四边形,梯形不是平行四边形,原题说法错误;
④四边形容易变形,四根分别长5cm,5cm,4cm,4cm的小棒能搭成很多不同形状的平行四边形,如长方形、不同的平行四边形,原题说法正确。
故答案为:A。
积的变化规律:一个因数扩大a倍,另一个因数缩小a倍,积不变;
计算被除数和除数末尾有0的除法,同时缩小相同的倍数,商不变,余数会缩小相同的倍数;
长方形、正方形是特殊的平行四边形,梯形不是平行四边形;
平行四边形容易变形,四条边的长度固定,但是它的形状可以发生变化。
8.A
解:露出的是一个钝角,所以后面的图形不可能是锐角三角形。
故答案为:A。
钝角三角形、梯形、平行四边形都有钝角,锐角三角形三个角都是锐角。
9.无数;相等
解:两条平行线之间可以画无数条垂线段,垂线段的长度相等。
故答案为:无数;相等。
两条平行线间垂线段的长度就是两条平行线之间的距离,两条平行线间的距离处处相等。
10.6;18
解:3+2+1=6(个)
6+6+6=18(个)。
故答案为:6;18。
有两组对边平行且相等的四边形是平行四边形,有一组对边平行的四边形是梯形。通过观察可知,第一个图形:单个的平行四边形有3个,由两个平行四边形组成的平行四边形有2个,由三个平行四边形组成的平行四边形有1个,因此共6个平行四边形。第二个图形:单个的梯形有6个,由两个梯形组成的梯形有7个,由三个梯形组成的梯形有2个,由四个梯形组成的梯形有2个,由六个梯形组成的梯形有1个,共18个。
11.24;27
解:80÷2-16=24(cm),所以与它相邻的一条边的长是24cm;(80-26)÷2=27(cm),所以这个梯形的腰长是27cm。
故答案为:24;27。
平行四边形相邻两边之和=铁丝的长度÷2-其中一条边的长度;
等腰梯形的腰=(铁丝的长度-上下底之和)÷2。
12.平行四边形;梯形
解:如果遮住的另一条边与对边平行,则平行四边形;如果遮住的另一条边不与对边平行,则是梯形。
故答案为:平行四边形;梯形。
两组对边分别平行的四边形叫做平行四边形;
只有一组对边平行的四边形叫做梯形。
13.梯
解:丙中有两条边互相平行,另外两条边不平行,所以丙是梯形。
故答案为:梯。
乙是梯形,甲是平行四边形,所以乙和甲所在的两条直线平行,乙和丙所在的两条直线不平行,丙和甲所在的两条直线平行。所以丙是梯形。
14.(1)短
(2)相等
解:(1)从直线外一点到这条直线所画的所有线段中,垂直线段最短;
(2)端点分别在两条平行线上,且与平行线垂直的所有线段的长度都相等。
故答案为:(1)短;(2)相等。
(1)从直线外一点到这条直线所画的所有线段中,垂直线段最短;
(2)两条平行线间的距离相等。
15.4;2.5
解:直角梯形有4个,梯形ABCD的高是2.5cm。
故答案为:4;2.5。
直角梯形:有两个直角的梯形。所以如图 、 、 、 一共4个直角梯形;
梯形的高:上底与下底之间的距离就是梯形的高。如图 ,看图可知梯形的高与长方形的宽一样长,所以梯形的高是2.5cm。
16.OA;OB;OC;OD;OE;OC
解:从点 O 引出的五条线段分别是:OA、OB、OC、OD、OE,其中最短的一条线段是OC。
故答案为:OA;OB;OC;OD;OE;OC。
此题主要考查了点到直线的距离,从直线外一点到这条直线所画的垂直线段最短,这条线段叫点到直线的距离。
17.
解:按照题意,可以得知,ABC是在一条直线上,否则形不成AC=12厘米,同样,ADE也在一条直线上.
因为:△EAB面积是24平方厘米,而只有角A是90度直角时,其面积才是:AB×(AD+DE)÷2=8×6÷2=24,
所以,角A是直角.
A是直角,则△CAD也是直角三角形,
根据勾股定理CD×CD=AD2+AC2,
解得CD=13厘米.
设:点A到CD的距离为x(也就是CD边上的高)列出方程:
解得,
故答案为:
通过应用勾股定理确定三角形CAD的形状。确定三角形CAD形状后,即可计算出CD的长度。通过三角形CAD的面积除以CD的长度即可计算点A到直线CD的距离
18.平行四边;长方形的对边互相平行,两个长方形如图重叠,组成的图形的对边分别平行,是一个平行四边形;4;35
解:阴影部分是一个平行四边形,理由是长方形的对边互相平行,两个长方形如图重叠,组成的图形的对边分别平行,是一个平行四边形,这个图形的高是4厘米;
因为∠1+∠2=90°,∠2+∠3=90°,又知∠1+∠2+∠3=125°,所以∠3=125°-(∠1+∠2)=125°-90°=35°。
故答案为:平行四边;长方形的对边互相平行,两个长方形如图重叠,组成的图形的对边分别平行,是一个平行四边形;4;35。
长方形的特征:两组对边互相平行且相等,四个角都是直角,两个长方形如图重叠,组成的图形是一个平行四边形,因为长方形的对边互相平行,两个长方形如图重叠,组成的图形的对边分别平行,是一个平行四边形;平行四边形的高是长方形的宽;
观察图可知,∠1+∠2=90°,∠2+∠3=90°,又知∠1+∠2+∠3=125°,代入即可求出∠3的度数。
19.三角形;平行四边形
解:由图可知:当梯形的上底逐渐缩小到一点时,梯形就转化成三角形;当梯形的上底增大到与下底相等时,梯形就转化成平行四边形;
故答案为:三角形,平行四边形.
此题应结合图形进行分析、解答即可.
20.2;4
解:如果要求在图内交叉点中再选一个点D,若要使四边形ABCD成为一个平行四边形,那么点D的选法共有2种,若要使四边形ABCD成为一个梯形,那么点D的选法共有4种。
故答案为:2;4。
若要使四边形ABCD成为一个平行四边形,D可以在C点左、右的3个长度的地方,那么点D的选法共有2种;若要使四边形ABCD成为一个梯形,那么点D的选法共有4种,分别在C点左、右1个、2个长度的地方。
21.(24+16)×2= 80(厘米)
22.解:图中所画的线段,就是他最快游上岸的路线,
从直线外一点到这条直线的所有线段中,垂直线段最短,它的长度叫做点到直线的距离。
23.(1)2;30
(2)解:
(3)解:
(4)解:
解:(1)测量图上线段AB=2厘米,∠1=30°。
故答案为:(1)2;30。
(1)测量线段的长度,先把0刻度线与一个顶点重合,观察另一端所指的刻度;
测量角的度数时,先把量角器的中心和角的顶点重合,把0°刻度线与角的一条边重合,然后观察另一条边所指的刻度;
(2)过直线外一点做这条直线的平行线,先把三角尺的一条直角边和这条直线重合,把直尺和另一条直角边重合,保证直尺不动,平移三角尺,直到这个点出现在第一条直角边上,然后沿着这条边画线即可;
(3)过直线外一点,做这条直线的垂线,先把三角尺的一条直角边与这条直线重合,然后平移三角尺,直到这个点出现在另一条直角边上,然后沿着这条边画线即可;
(4)用量角器画角时,先画出角的顶点和一条边,把量角器的中心和角的顶点重合,把0°刻度线和角的另一条边重合,再在量角器上找到所要画的刻度,并做上标记,最后把标记和顶点连接起来即可。
24.解:12÷2-4
=6-4
=2(分米)
4×2=8(平方分米)
答:长方形的面积是8平方分米。
根据“平行四边形的周长=邻边长之和×2”,可以求出平行四边形的两条邻边中另一条边的长度;拉动平行四边形变成长方形,两条邻边长不变,变为长方形的长和宽,根据“长方形的面积=长×宽”求解。
25.解: (45 +40)×2
=85×2
= 170(厘米)
答:需要的框的周长是170厘米。
平行四边形两条邻边的长度和×2=平行四边形的周长。
26.解:甲是平行四边形,说明a∥b,f∥e,
乙是梯形,说明d不平行c,
图形丙,左右平行,上下不平行,说明丙是梯形。
两组对边分别平行的四边形叫做平行四边形;一组对边平行而另一组对边不平行的四边形是梯形;据此解答。
27.3.6÷(2.88÷1.2)=1.5(小时)
28.解:48÷2-15
=24-15
=9(厘米)
答:这个平行四边形的四条边分别是15厘米、9厘米、15厘米、9厘米。
长方形框架的长与宽之和=长方形框架的周长÷2,所以长方形的宽=长方形的长与宽之和-长方形的长;
把长方形拉成平行四边形后,长方形的长是平行四边形的底,长方形的宽是平行四边形的腰。
29.解:30÷(4-1)
=30÷3
=10(厘米)
10×4=40(厘米)
答:这个梯形的上底是10厘米,下底是40厘米。
梯形的下底的长度是上底的4倍,可以把下底看成4份,上底看成1份,下底比上底多3份;又因为上底延长30厘米这个梯形就变成了平行四边形,平行四边形对边平行且相等,则多出的3份对应30厘米;算出每一份是的长度,也就求出了上底的长度,再乘以4即为下底的长度。
同课章节目录
