2024-2025学年四年级数学上册寒假巩固练习(北师大版)第2练-线与角 (含解析)
文档属性
| 名称 | 2024-2025学年四年级数学上册寒假巩固练习(北师大版)第2练-线与角 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 439.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-21 19:24:08 | ||
图片预览



文档简介
2024-2025学年四年级数学上册寒假巩固练习(北师大版)
第2练-线与角
一、填空(共19分)
1.如下图,B、C、D依次是线段AE上三点,已知BD=3cm,则图中以A、B、C、D、E这五个点为端点的所有线段长度之和等于 。
2. 以下图形中各有几组平行线段、几组垂直线段
平行线段 组 组 组
垂直线段 组 组 组
3.如图, ⊥ , ∥ 。在点A与CG边上的点相连的线段中, 最短。
4.把一条线段向两端无限延伸就得到一条 ,向一端无限延伸就得到一条 。
5.下图是奇思家到中心书城的路线图,有 条路可以走,第 (填序号)条路最近,因为两点之间所有连线中, 最短。
6.在同一平面内有三条直线,如果a⊥b,b∥c,那么a c。(填“⊥”或“∥”)
7.角是从 点引出 条射线所组成的图形;测量角的大小所用的工具是 。
8.1周角= °, °角的4倍是1周角。
9. 分一分,填一填。
65° 20° 117° 112° 90° 86°
180° 170° 33° 360°
(1)锐角
(2)直角
(3)钝角
(4)平角
(5)周角
10.照样子,用词语形容下面三种线。
二、判断(共10分)
11.下图中,∠1=∠2。( )
12.从6:15到6:30,分针绕中心点顺时针方向旋转了15°。( )
13.两个锐角拼成一个更大的角,这个更大的角一定小于平角。( )
14. 将圆平均分成360分,把其中一份所对的角作为角的单位。( )
15.把一张长方形的纸连续对折两次后展开,折痕可能互相平行,也可能互相垂直。( )
三、选择(共10分)
16. 如图,图中共有( )条线段。
A.1 B.2 C.3 D.4
17.直角、钝角、平角、锐角按从大到小的顺序排列正确的是( ) 。
A.直角、锐角、平角、钝角 B.平角、钝角、直角、锐角
C.钝角、平角、直角、锐角 D.锐角、直角、钝角、平角
18.把一张长方形纸片对折2次,展开后看到的折痕( )。
A.一定互相平行
B.一定互相垂直
C.可能互相平行,也可能互相垂直
D.既不平行,也不垂直
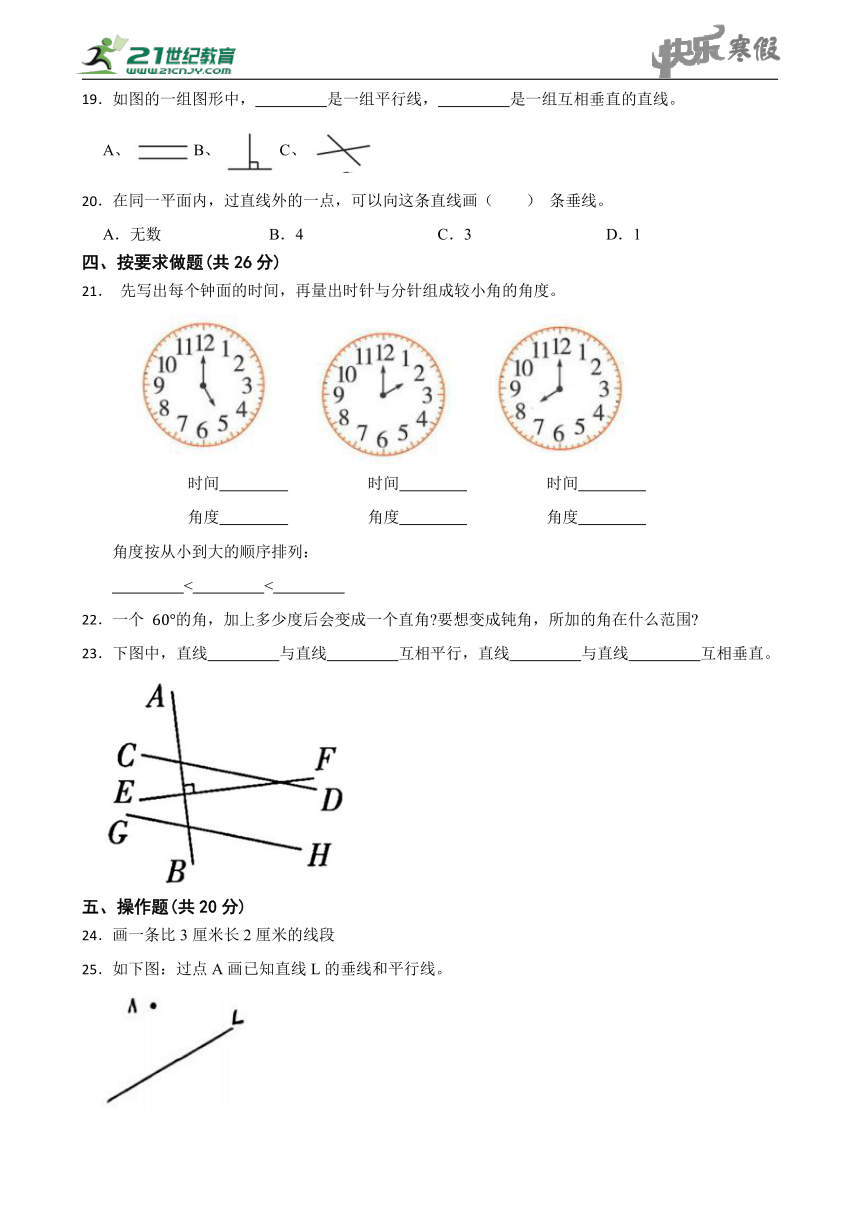
19.如图的一组图形中, 是一组平行线, 是一组互相垂直的直线。
A、B、C、
20.在同一平面内,过直线外的一点,可以向这条直线画( ) 条垂线。
A.无数 B.4 C.3 D.1
四、按要求做题(共26分)
21. 先写出每个钟面的时间,再量出时针与分针组成较小角的角度。
时间 角度 时间 角度 时间 角度
角度按从小到大的顺序排列:
< <
22.一个 的角,加上多少度后会变成一个直角 要想变成钝角,所加的角在什么范围
23.下图中,直线 与直线 互相平行,直线 与直线 互相垂直。
五、操作题(共20分)
24.画一条比3厘米长2厘米的线段
25.如下图:过点A画已知直线L的垂线和平行线。
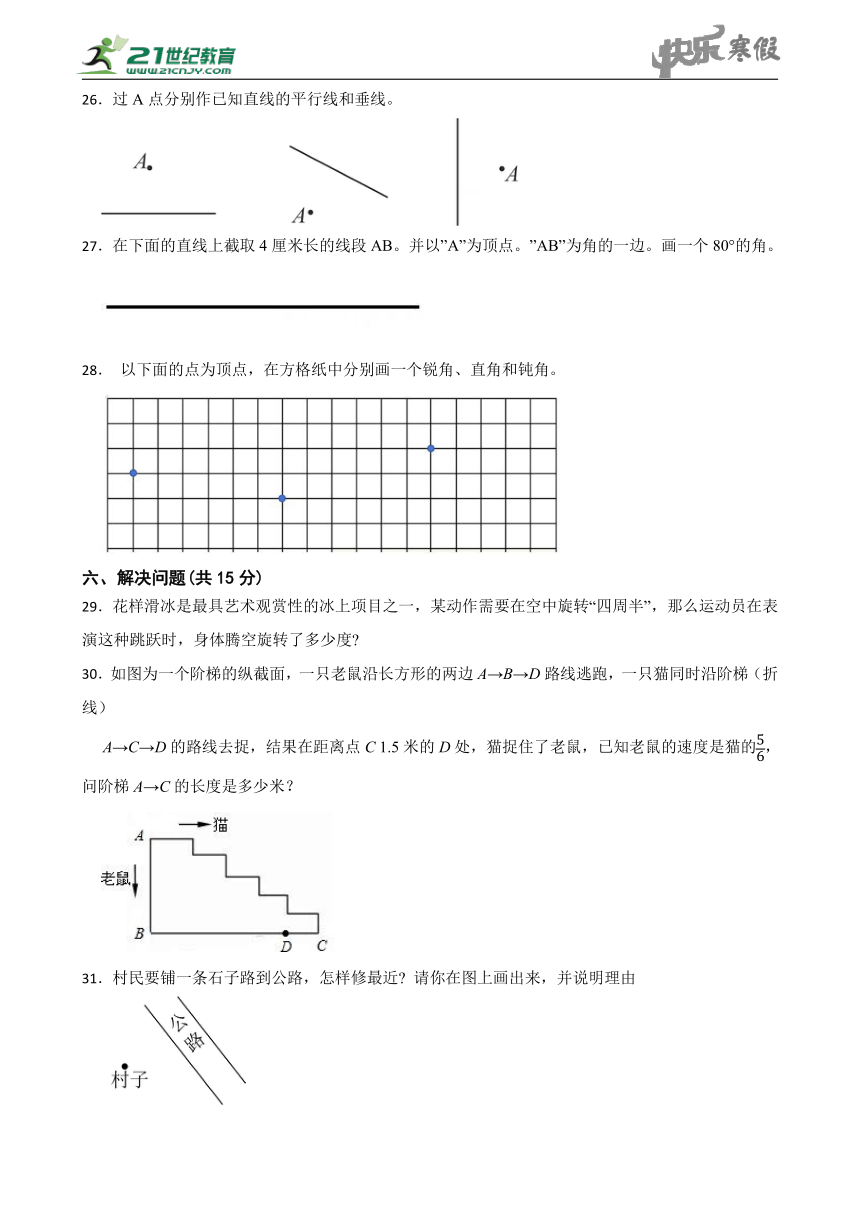
26.过A点分别作已知直线的平行线和垂线。
27.在下面的直线上截取4厘米长的线段AB。并以”A”为顶点。”AB”为角的一边。画一个80°的角。
28. 以下面的点为顶点,在方格纸中分别画一个锐角、直角和钝角。
六、解决问题(共15分)
29.花样滑冰是最具艺术观赏性的冰上项目之一,某动作需要在空中旋转“四周半”,那么运动员在表演这种跳跃时,身体腾空旋转了多少度
30.如图为一个阶梯的纵截面,一只老鼠沿长方形的两边A→B→D路线逃跑,一只猫同时沿阶梯(折线)
A→C→D的路线去捉,结果在距离点C 1.5米的D处,猫捉住了老鼠,已知老鼠的速度是猫的,问阶梯A→C的长度是多少米?
31.村民要铺一条石子路到公路,怎样修最近 请你在图上画出来,并说明理由
七、附加题(共10分)
32.如下图,∠1=∠2=∠3,所有小于90°的角的度数和是 180°,求∠AOB的度数。
答案解析部分
1.41.6㎝
解:根据题意:图中的线段有 AB、AC 、 AD 、 AE 、 BC 、 BD 、 BE 、 CD 、 CE 、 DE ,且 A E 长为8.9cm, BD 为3cm,
则线段 AE 上所有线段的长度的总和为: AB + AC+ AD + AE + BC + BD + BE + CD + CE + DE =4AE +2BD=41.6cm.
故答案为:41.6.
图中包含的线段有 AB 、 AC 、 AD 、 AE 、 BC 、 BD 、 BE 、 CD 、 CE 、 DE ,则线段 AE 上所有线段的长度的总和为: AB + AC + AD + AE + B C + BD + BE + CD + CE + DE ,且 AE 长为8.9cm, BD 为3cm,即可求出答案.
2.2;1;5;4;2;0
解:
平行线段 2组 1组 5组
垂直线段 4组 2组 0组
故答案为:2;1;5;4;2;0。
在同一平面内,两条直线相交成直角,这两条直线叫做互相垂直;在同一平面内不相交的两条直线,叫做互相平行。据此数一数。
3.AF;CG;AF;BC;AF
解:AF⊥CG,AF∥BC;在点A与CG边上的点相连的线段中,AF最短。
故答案为:AF;CG;AF;BC;AF。
在同一平面内,两条直线相交成直角,这两条直线叫做互相垂直;在同一平面内不相交的两条直线,叫做互相平行;
直线外一点到这条直线的垂直线段最短。
4.直线;射线
解:把一条线段向两端无限延伸就得到一条直线 ,向一端无限延伸就得到一条射线。
故答案为:直线;射线。
线段有2个端点,有具体的长度;直线没有端点、直线可以向两方无限延伸,射线有1个端点,可以向一方无限延伸,直线射线都没有具体的长度。
5.两;③;线段
6.⊥
解:如果a⊥b,b∥c,那么a⊥c。
故答案为:⊥。
在同一平面内的两条平行线,垂直于其中一条直线的直线也垂直于另一条直线。
7.一;两;量角器
解:角是从一点引出两条射线所组成的图形;测量角的大小所用的工具是量角器。
故答案为:一;两;量角器。
根据角的概念及度量相关知识可解。
8.360;90
解:1周角=360°;360°÷4=90°,90°角的4倍是1周角。
故答案为:360;90。
1直角=90°;1周角=360°;据此解答。
9.(1)65°、20°、86°、33°
(2)90°
(3)117°,112°,170
(4)180°
(5)360°
解:(1)钝角有:65°、20°、86°、33°;
(2)直角是:90°;
(3)钝角有:117°,112°,170;
(4)平角是:180°;
(5)周角是:360°。
故答案为:(1)65°,20°,86°,33°;(2)90°;(3)117°,112°,170;(4)180°;(5)360°。
锐角是大于0°小于90°的角;直角是等于90°的角;钝角是大于90°小于180°的角;平角是等于180°的角;周角是等于360°的角。据此作答即可。
10.
直线没有端点,无限长,用无始无终表示;射线只有一个端点,无限长,用有始无终来表示;线段有2个端点,有限长,用有始有终来表示。
11.正确
解:因为∠1+中间的角=90度,∠2+中间的角=90度,
所以∠1=∠2。原题说法正确。
故答案为:正确。
一个加数相等,和相等,那么另一个加数也相等。
12.错误
解:6时30分-6时15分=15分
30°×3=90°。
故答案为:错误。
钟面上共12个大格,平均每个大格是30°,从6:15到6:30,分针走了3个大格, 分针绕中心点顺时针方向旋转的度数=30°×大格个数。
13.正确
解:两个锐角都小于90°,拼成的更大的角一定小于180°。原题说法正确。
故答案为:正确。
小于90°的角叫锐角;1平角=180°;据此解答。
14.正确
将圆平均分成360分,把其中一份所对的角作为角的单位。原题说法正确。
故答案为:正确。
其中一份所对的角的度数是1度,角的单位就是1度。
15.正确
解:把一张长方形的纸连续对折两次后展开,折痕可能互相平行,也可能互相垂直。说法正确。
故答案为:正确。
两次对折的方向平行,两条折痕也互相平行;两次对折的方向垂直,两条折痕也互相垂直。
16.C
解:3×(3-1)÷2=3(条),图中共有3条线段。
故答案为:C。
n表示一条线段上点的个数,线段的总条数=n×(n-1)÷2。
17.B
解:直角、钝角、平角、锐角按从大到小的顺序排列是:平角、钝角、直角、锐角。
故答案为:B。
角的分类:0°<锐角<90°,直角=90°,90°<钝角<180°,锐角<直角<钝角,平角=180°,周角=360°,据此解答。
18.C
解:把一张长方形纸片朝着相同的方向对折2次,展开后看到的折痕互相平行;朝着不同的方向对折2次,展开后看到的折痕互相垂直。
故答案为:C。
把一张长方形纸片对折2次,展开后看到的折痕可能互相平行,也可能互相垂直。
19.A;B
A选项图形为一组平行线,B选项图形是一组互相垂直的直线。
故答案为:A;B。
在同一平面内不相交的两条直线叫做平行线,平行线永不相交;如果两条直线相交成直角,就说这两条直线互相垂直;据此解答即可。
20.D
解:在同一平面内,过直线外的一点,可以向这条直线画1条垂线。
故答案为:D。
过直线外一点,有且只有一条直线与已知直线垂直。
21.5:00;150°;2:00;60°;8:00;120°;60°;120°;150°
解:第一个钟面的时间是5:00,角度是30°×5=150°;
第二个钟面的时间是2:00,角度是30°×2=60°;
第三个钟面的时间是8:00,角度是30°×4=120°;
角度按从小到大的顺序排列是:60°<120°<150°。
故答案为:5:00;150°;2:00;60°;8:00;120°;60°;120°;150°。
钟面上一大格是30°,钟面上时针和分针夹了几大格,夹角就是(几×30°)。
22.解:90°-60°=30°
180°-60°=120°
答:加上30°后会变成直角;要想变成钝角,所加的角应大于30°且小于120°。
直角是90°;钝角是大于90°小于180°。据此作答即可。
23.CD;GH;AB;EF
解:观察图,直线CD与直线GH互相平行,直线AB与直线EF互相垂直。
故答案为:CD;GH;AB;EF。
根据垂直和平行的性质:在同一平面内相交成直角的两条直线叫做互相垂直,不相交的两条直线叫做平行线,据此判断即可。
24.3+2=5(厘米)
所以可得图:
求出比3厘米长2厘米的线段长度,然后画出线段。
25.解:
过A点作垂线的方法:先把三角尺的一条直角边与直线L重合;沿着直线移动三角尺,使A点在三角尺的另一条直角边上。再沿三角尺的另一条直角边画一条直线,并画上垂直符号。这条直线就是直线L的垂线。
(过A作直线L的平行线的方法:先把三角尺的一条直角边与直线L重合;再用直尺紧靠着三角尺的另一条直角边。固定直尺,然后沿着直尺平移三角尺,使A点在三角尺上。沿直角边画出另一条直线即可。
26.
(1)过直线外一点画已知直线垂线的方法:先用直尺与已知直线对齐,再用直角三角板的一条直角边与直尺对齐,移动三角板使另一条直角边与点对齐,沿这条直角边过点画直线,这条直线即所需要画的垂线(移动过程中不要移动直尺也要保证三角板与直尺对齐)。
(2)过直线外一点画已知直线平行线的方法:先将三角板的一条直角边与直尺边对齐,然后将三角板的另一条直角边与已知直线对齐,按住直尺不动,平移三角板使直角边与点对齐,最后过点画直线,这条直线即为已知直线的平行线。
27.解:
线段A点对准尺的0刻度,另一端对着刻度4,截取的线段的长度就是4厘米;
用量角器量角的方法:把量角器的中心和角的顶点重合,0°刻度线和角的一条边重合;角的另一边所对的量角器上的刻度,就是这个角的度数。
28.解:
锐角比直角小,钝角比直角大,据此画出各角。
29.解:360°×5+360°÷2
=1440°+180°
=1620°
答:身体腾空旋转了1620°。
一周是360度,半周是180度,四周半是4个360度+180度,据此解答。
30.解:把楼梯的各条线段进行平移,可得AB+BC=楼梯A→C的总长;
设A→C的路程为x米,则猫行走的路程为x+1.5米,老鼠行走的路程为x-1.5米,
因为猫和老鼠行走的时间相同,且老鼠的速度是猫的,根据时间一定时,路程与速度成正比的性质可得:
解得,
答: 阶梯A→C的长度是16.5米
如图,把楼梯的各条线段进行平移,可得到一个长方形ABCE;可得AB+BC=楼梯A→C的总长(即这个长方形周长的一半) ;猫捉鼠的路程之和为楼梯A→C的总长+线段CD长;老鼠逃窜的路程为AB+BC-线段CD长;根据时间一定时, 所行走的路程与速度成正比的性质即可解决问题
31.解:
点到直线的垂线段最短。
用三角尺过直线外一点画已知直线垂线的方法:①把三角尺的一条直角边与已知直线重合;②沿着直线移动三角尺,使三角尺的另一条直角边通过直线外的点,沿这条直角边画一条直线;③在垂足处标出垂直符号,据此作图;
点到直线的垂线中,垂线段距离最短。
32.解:∠1+∠2+∠3+(∠1+∠2)+(∠2+∠3)+(∠1+∠2+∠3)=180°
又因为∠1=∠2=∠3,所以 10×∠1=180°,∠1=18°;
∠AOB=∠1+∠2+∠3=3×∠1=18°×3=54°。
看图可知最大角是∠AOB,小于 90°,说明所有的角都小于90°。图中基本角有3个,由两个基本角组成的角有2个,由三个基本角组成的角有1个。一共有1×3+2×2+3×1=10(个)基本角,它们的和是180°,由此可以求出基本角的度数。∠AOB是由三个基本角组成的,用基本角的度数乘 3 即可。
第2练-线与角
一、填空(共19分)
1.如下图,B、C、D依次是线段AE上三点,已知BD=3cm,则图中以A、B、C、D、E这五个点为端点的所有线段长度之和等于 。
2. 以下图形中各有几组平行线段、几组垂直线段
平行线段 组 组 组
垂直线段 组 组 组
3.如图, ⊥ , ∥ 。在点A与CG边上的点相连的线段中, 最短。
4.把一条线段向两端无限延伸就得到一条 ,向一端无限延伸就得到一条 。
5.下图是奇思家到中心书城的路线图,有 条路可以走,第 (填序号)条路最近,因为两点之间所有连线中, 最短。
6.在同一平面内有三条直线,如果a⊥b,b∥c,那么a c。(填“⊥”或“∥”)
7.角是从 点引出 条射线所组成的图形;测量角的大小所用的工具是 。
8.1周角= °, °角的4倍是1周角。
9. 分一分,填一填。
65° 20° 117° 112° 90° 86°
180° 170° 33° 360°
(1)锐角
(2)直角
(3)钝角
(4)平角
(5)周角
10.照样子,用词语形容下面三种线。
二、判断(共10分)
11.下图中,∠1=∠2。( )
12.从6:15到6:30,分针绕中心点顺时针方向旋转了15°。( )
13.两个锐角拼成一个更大的角,这个更大的角一定小于平角。( )
14. 将圆平均分成360分,把其中一份所对的角作为角的单位。( )
15.把一张长方形的纸连续对折两次后展开,折痕可能互相平行,也可能互相垂直。( )
三、选择(共10分)
16. 如图,图中共有( )条线段。
A.1 B.2 C.3 D.4
17.直角、钝角、平角、锐角按从大到小的顺序排列正确的是( ) 。
A.直角、锐角、平角、钝角 B.平角、钝角、直角、锐角
C.钝角、平角、直角、锐角 D.锐角、直角、钝角、平角
18.把一张长方形纸片对折2次,展开后看到的折痕( )。
A.一定互相平行
B.一定互相垂直
C.可能互相平行,也可能互相垂直
D.既不平行,也不垂直
19.如图的一组图形中, 是一组平行线, 是一组互相垂直的直线。
A、B、C、
20.在同一平面内,过直线外的一点,可以向这条直线画( ) 条垂线。
A.无数 B.4 C.3 D.1
四、按要求做题(共26分)
21. 先写出每个钟面的时间,再量出时针与分针组成较小角的角度。
时间 角度 时间 角度 时间 角度
角度按从小到大的顺序排列:
< <
22.一个 的角,加上多少度后会变成一个直角 要想变成钝角,所加的角在什么范围
23.下图中,直线 与直线 互相平行,直线 与直线 互相垂直。
五、操作题(共20分)
24.画一条比3厘米长2厘米的线段
25.如下图:过点A画已知直线L的垂线和平行线。
26.过A点分别作已知直线的平行线和垂线。
27.在下面的直线上截取4厘米长的线段AB。并以”A”为顶点。”AB”为角的一边。画一个80°的角。
28. 以下面的点为顶点,在方格纸中分别画一个锐角、直角和钝角。
六、解决问题(共15分)
29.花样滑冰是最具艺术观赏性的冰上项目之一,某动作需要在空中旋转“四周半”,那么运动员在表演这种跳跃时,身体腾空旋转了多少度
30.如图为一个阶梯的纵截面,一只老鼠沿长方形的两边A→B→D路线逃跑,一只猫同时沿阶梯(折线)
A→C→D的路线去捉,结果在距离点C 1.5米的D处,猫捉住了老鼠,已知老鼠的速度是猫的,问阶梯A→C的长度是多少米?
31.村民要铺一条石子路到公路,怎样修最近 请你在图上画出来,并说明理由
七、附加题(共10分)
32.如下图,∠1=∠2=∠3,所有小于90°的角的度数和是 180°,求∠AOB的度数。
答案解析部分
1.41.6㎝
解:根据题意:图中的线段有 AB、AC 、 AD 、 AE 、 BC 、 BD 、 BE 、 CD 、 CE 、 DE ,且 A E 长为8.9cm, BD 为3cm,
则线段 AE 上所有线段的长度的总和为: AB + AC+ AD + AE + BC + BD + BE + CD + CE + DE =4AE +2BD=41.6cm.
故答案为:41.6.
图中包含的线段有 AB 、 AC 、 AD 、 AE 、 BC 、 BD 、 BE 、 CD 、 CE 、 DE ,则线段 AE 上所有线段的长度的总和为: AB + AC + AD + AE + B C + BD + BE + CD + CE + DE ,且 AE 长为8.9cm, BD 为3cm,即可求出答案.
2.2;1;5;4;2;0
解:
平行线段 2组 1组 5组
垂直线段 4组 2组 0组
故答案为:2;1;5;4;2;0。
在同一平面内,两条直线相交成直角,这两条直线叫做互相垂直;在同一平面内不相交的两条直线,叫做互相平行。据此数一数。
3.AF;CG;AF;BC;AF
解:AF⊥CG,AF∥BC;在点A与CG边上的点相连的线段中,AF最短。
故答案为:AF;CG;AF;BC;AF。
在同一平面内,两条直线相交成直角,这两条直线叫做互相垂直;在同一平面内不相交的两条直线,叫做互相平行;
直线外一点到这条直线的垂直线段最短。
4.直线;射线
解:把一条线段向两端无限延伸就得到一条直线 ,向一端无限延伸就得到一条射线。
故答案为:直线;射线。
线段有2个端点,有具体的长度;直线没有端点、直线可以向两方无限延伸,射线有1个端点,可以向一方无限延伸,直线射线都没有具体的长度。
5.两;③;线段
6.⊥
解:如果a⊥b,b∥c,那么a⊥c。
故答案为:⊥。
在同一平面内的两条平行线,垂直于其中一条直线的直线也垂直于另一条直线。
7.一;两;量角器
解:角是从一点引出两条射线所组成的图形;测量角的大小所用的工具是量角器。
故答案为:一;两;量角器。
根据角的概念及度量相关知识可解。
8.360;90
解:1周角=360°;360°÷4=90°,90°角的4倍是1周角。
故答案为:360;90。
1直角=90°;1周角=360°;据此解答。
9.(1)65°、20°、86°、33°
(2)90°
(3)117°,112°,170
(4)180°
(5)360°
解:(1)钝角有:65°、20°、86°、33°;
(2)直角是:90°;
(3)钝角有:117°,112°,170;
(4)平角是:180°;
(5)周角是:360°。
故答案为:(1)65°,20°,86°,33°;(2)90°;(3)117°,112°,170;(4)180°;(5)360°。
锐角是大于0°小于90°的角;直角是等于90°的角;钝角是大于90°小于180°的角;平角是等于180°的角;周角是等于360°的角。据此作答即可。
10.
直线没有端点,无限长,用无始无终表示;射线只有一个端点,无限长,用有始无终来表示;线段有2个端点,有限长,用有始有终来表示。
11.正确
解:因为∠1+中间的角=90度,∠2+中间的角=90度,
所以∠1=∠2。原题说法正确。
故答案为:正确。
一个加数相等,和相等,那么另一个加数也相等。
12.错误
解:6时30分-6时15分=15分
30°×3=90°。
故答案为:错误。
钟面上共12个大格,平均每个大格是30°,从6:15到6:30,分针走了3个大格, 分针绕中心点顺时针方向旋转的度数=30°×大格个数。
13.正确
解:两个锐角都小于90°,拼成的更大的角一定小于180°。原题说法正确。
故答案为:正确。
小于90°的角叫锐角;1平角=180°;据此解答。
14.正确
将圆平均分成360分,把其中一份所对的角作为角的单位。原题说法正确。
故答案为:正确。
其中一份所对的角的度数是1度,角的单位就是1度。
15.正确
解:把一张长方形的纸连续对折两次后展开,折痕可能互相平行,也可能互相垂直。说法正确。
故答案为:正确。
两次对折的方向平行,两条折痕也互相平行;两次对折的方向垂直,两条折痕也互相垂直。
16.C
解:3×(3-1)÷2=3(条),图中共有3条线段。
故答案为:C。
n表示一条线段上点的个数,线段的总条数=n×(n-1)÷2。
17.B
解:直角、钝角、平角、锐角按从大到小的顺序排列是:平角、钝角、直角、锐角。
故答案为:B。
角的分类:0°<锐角<90°,直角=90°,90°<钝角<180°,锐角<直角<钝角,平角=180°,周角=360°,据此解答。
18.C
解:把一张长方形纸片朝着相同的方向对折2次,展开后看到的折痕互相平行;朝着不同的方向对折2次,展开后看到的折痕互相垂直。
故答案为:C。
把一张长方形纸片对折2次,展开后看到的折痕可能互相平行,也可能互相垂直。
19.A;B
A选项图形为一组平行线,B选项图形是一组互相垂直的直线。
故答案为:A;B。
在同一平面内不相交的两条直线叫做平行线,平行线永不相交;如果两条直线相交成直角,就说这两条直线互相垂直;据此解答即可。
20.D
解:在同一平面内,过直线外的一点,可以向这条直线画1条垂线。
故答案为:D。
过直线外一点,有且只有一条直线与已知直线垂直。
21.5:00;150°;2:00;60°;8:00;120°;60°;120°;150°
解:第一个钟面的时间是5:00,角度是30°×5=150°;
第二个钟面的时间是2:00,角度是30°×2=60°;
第三个钟面的时间是8:00,角度是30°×4=120°;
角度按从小到大的顺序排列是:60°<120°<150°。
故答案为:5:00;150°;2:00;60°;8:00;120°;60°;120°;150°。
钟面上一大格是30°,钟面上时针和分针夹了几大格,夹角就是(几×30°)。
22.解:90°-60°=30°
180°-60°=120°
答:加上30°后会变成直角;要想变成钝角,所加的角应大于30°且小于120°。
直角是90°;钝角是大于90°小于180°。据此作答即可。
23.CD;GH;AB;EF
解:观察图,直线CD与直线GH互相平行,直线AB与直线EF互相垂直。
故答案为:CD;GH;AB;EF。
根据垂直和平行的性质:在同一平面内相交成直角的两条直线叫做互相垂直,不相交的两条直线叫做平行线,据此判断即可。
24.3+2=5(厘米)
所以可得图:
求出比3厘米长2厘米的线段长度,然后画出线段。
25.解:
过A点作垂线的方法:先把三角尺的一条直角边与直线L重合;沿着直线移动三角尺,使A点在三角尺的另一条直角边上。再沿三角尺的另一条直角边画一条直线,并画上垂直符号。这条直线就是直线L的垂线。
(过A作直线L的平行线的方法:先把三角尺的一条直角边与直线L重合;再用直尺紧靠着三角尺的另一条直角边。固定直尺,然后沿着直尺平移三角尺,使A点在三角尺上。沿直角边画出另一条直线即可。
26.
(1)过直线外一点画已知直线垂线的方法:先用直尺与已知直线对齐,再用直角三角板的一条直角边与直尺对齐,移动三角板使另一条直角边与点对齐,沿这条直角边过点画直线,这条直线即所需要画的垂线(移动过程中不要移动直尺也要保证三角板与直尺对齐)。
(2)过直线外一点画已知直线平行线的方法:先将三角板的一条直角边与直尺边对齐,然后将三角板的另一条直角边与已知直线对齐,按住直尺不动,平移三角板使直角边与点对齐,最后过点画直线,这条直线即为已知直线的平行线。
27.解:
线段A点对准尺的0刻度,另一端对着刻度4,截取的线段的长度就是4厘米;
用量角器量角的方法:把量角器的中心和角的顶点重合,0°刻度线和角的一条边重合;角的另一边所对的量角器上的刻度,就是这个角的度数。
28.解:
锐角比直角小,钝角比直角大,据此画出各角。
29.解:360°×5+360°÷2
=1440°+180°
=1620°
答:身体腾空旋转了1620°。
一周是360度,半周是180度,四周半是4个360度+180度,据此解答。
30.解:把楼梯的各条线段进行平移,可得AB+BC=楼梯A→C的总长;
设A→C的路程为x米,则猫行走的路程为x+1.5米,老鼠行走的路程为x-1.5米,
因为猫和老鼠行走的时间相同,且老鼠的速度是猫的,根据时间一定时,路程与速度成正比的性质可得:
解得,
答: 阶梯A→C的长度是16.5米
如图,把楼梯的各条线段进行平移,可得到一个长方形ABCE;可得AB+BC=楼梯A→C的总长(即这个长方形周长的一半) ;猫捉鼠的路程之和为楼梯A→C的总长+线段CD长;老鼠逃窜的路程为AB+BC-线段CD长;根据时间一定时, 所行走的路程与速度成正比的性质即可解决问题
31.解:
点到直线的垂线段最短。
用三角尺过直线外一点画已知直线垂线的方法:①把三角尺的一条直角边与已知直线重合;②沿着直线移动三角尺,使三角尺的另一条直角边通过直线外的点,沿这条直角边画一条直线;③在垂足处标出垂直符号,据此作图;
点到直线的垂线中,垂线段距离最短。
32.解:∠1+∠2+∠3+(∠1+∠2)+(∠2+∠3)+(∠1+∠2+∠3)=180°
又因为∠1=∠2=∠3,所以 10×∠1=180°,∠1=18°;
∠AOB=∠1+∠2+∠3=3×∠1=18°×3=54°。
看图可知最大角是∠AOB,小于 90°,说明所有的角都小于90°。图中基本角有3个,由两个基本角组成的角有2个,由三个基本角组成的角有1个。一共有1×3+2×2+3×1=10(个)基本角,它们的和是180°,由此可以求出基本角的度数。∠AOB是由三个基本角组成的,用基本角的度数乘 3 即可。
同课章节目录
