第十七章勾股定理(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第十七章勾股定理
一、单选题
1.如图所示,在数轴上点A所表示的数为a,则a的值为( )
A. B. C. D.
2.如图,长方形门框高为2m,宽为1.5m,现有3块木板,尺寸如下:①号木板长3m,宽2.7m;②号木板长4m,宽2.4m;③号木板长2.8m,宽2.6m.能从这扇门通过的木板是( )
A.① B.② C.③号 D.都不能通过
3.如图,Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD平分∠CAB,交BC于D,DE⊥AB于E,则CD等于( )
A.2cm B.3cm C.4cm D.5cm
4.图中的四边形均为正方形,三角形为直角三角形,最大的正方形的边长为7cm,则图中A、B两个正方形的面积之和为( )
A.28cm2 B.42cm2 C.49cm2 D.63cm2
5.在下列由线段组成的三角形中,是直角三角形的是( )
A.,, B.,,
C.,, D.,,
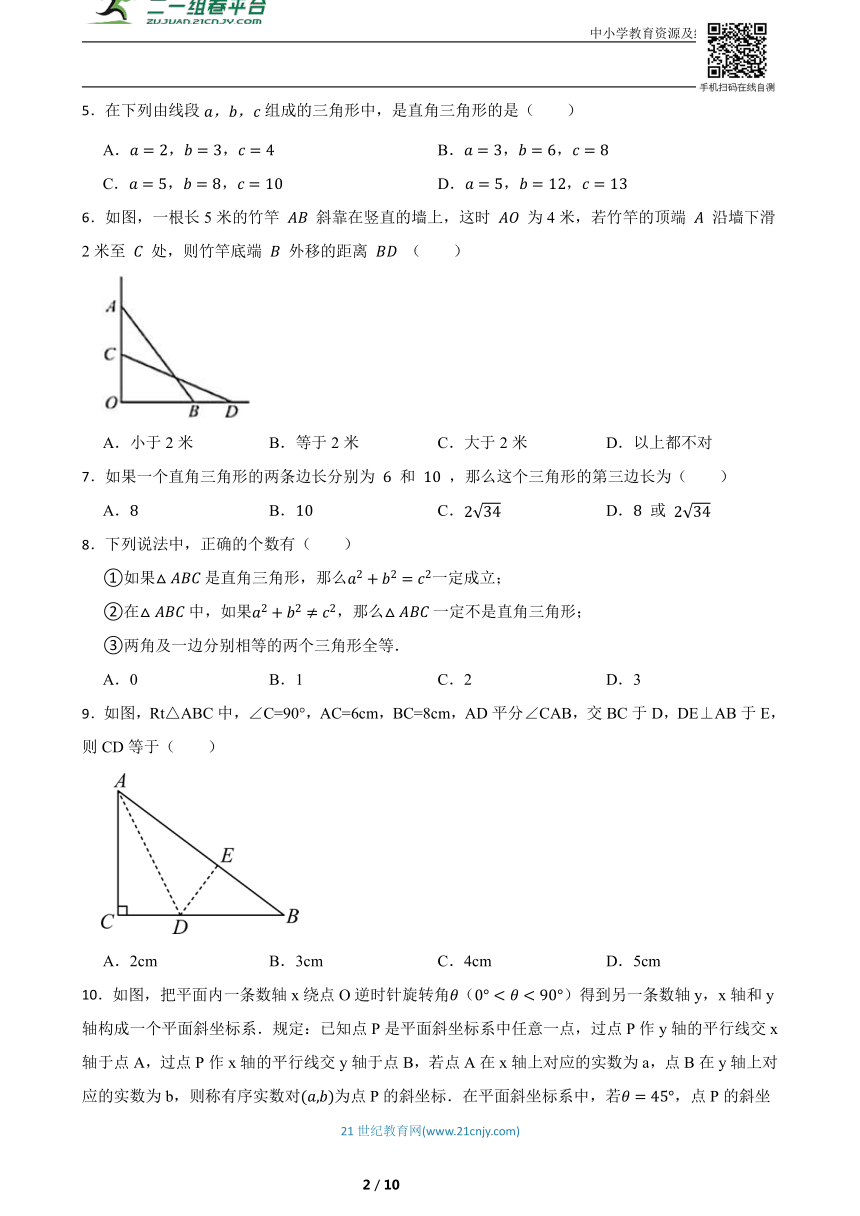
6.如图,一根长5米的竹竿 斜靠在竖直的墙上,这时 为4米,若竹竿的顶端 沿墙下滑2米至 处,则竹竿底端 外移的距离 ( )
A.小于2米 B.等于2米 C.大于2米 D.以上都不对
7.如果一个直角三角形的两条边长分别为 和 ,那么这个三角形的第三边长为( )
A. B. C. D. 或
8.下列说法中,正确的个数有( )
①如果是直角三角形,那么一定成立;
②在中,如果,那么一定不是直角三角形;
③两角及一边分别相等的两个三角形全等.
A.0 B.1 C.2 D.3
9.如图,Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD平分∠CAB,交BC于D,DE⊥AB于E,则CD等于( )
A.2cm B.3cm C.4cm D.5cm
10.如图,把平面内一条数轴x绕点O逆时针旋转角()得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:已知点P是平面斜坐标系中任意一点,过点P作y轴的平行线交x轴于点A,过点P作x轴的平行线交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对为点P的斜坐标.在平面斜坐标系中,若,点P的斜坐标为,点G的斜坐标为,连接,则线段的长度是( )
A. B. C. D.
二、填空题
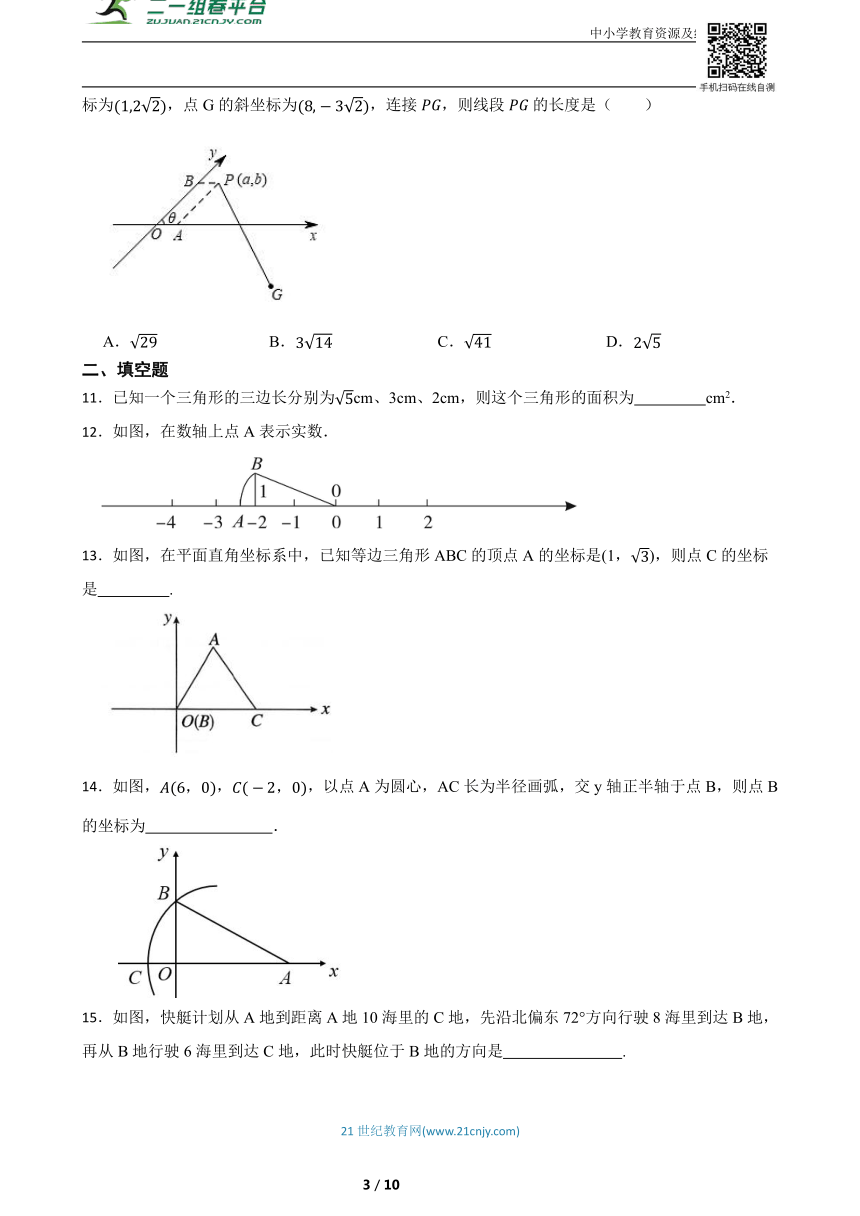
11.已知一个三角形的三边长分别为cm、3cm、2cm,则这个三角形的面积为 cm2.
12.如图,在数轴上点A表示实数.
13.如图,在平面直角坐标系中,已知等边三角形ABC的顶点A的坐标是(1,),则点C的坐标是 .
14.如图,,,以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为 .
15.如图,快艇计划从A地到距离A地10海里的C地,先沿北偏东72°方向行驶8海里到达B地,再从B地行驶6海里到达C地,此时快艇位于B地的方向是 .
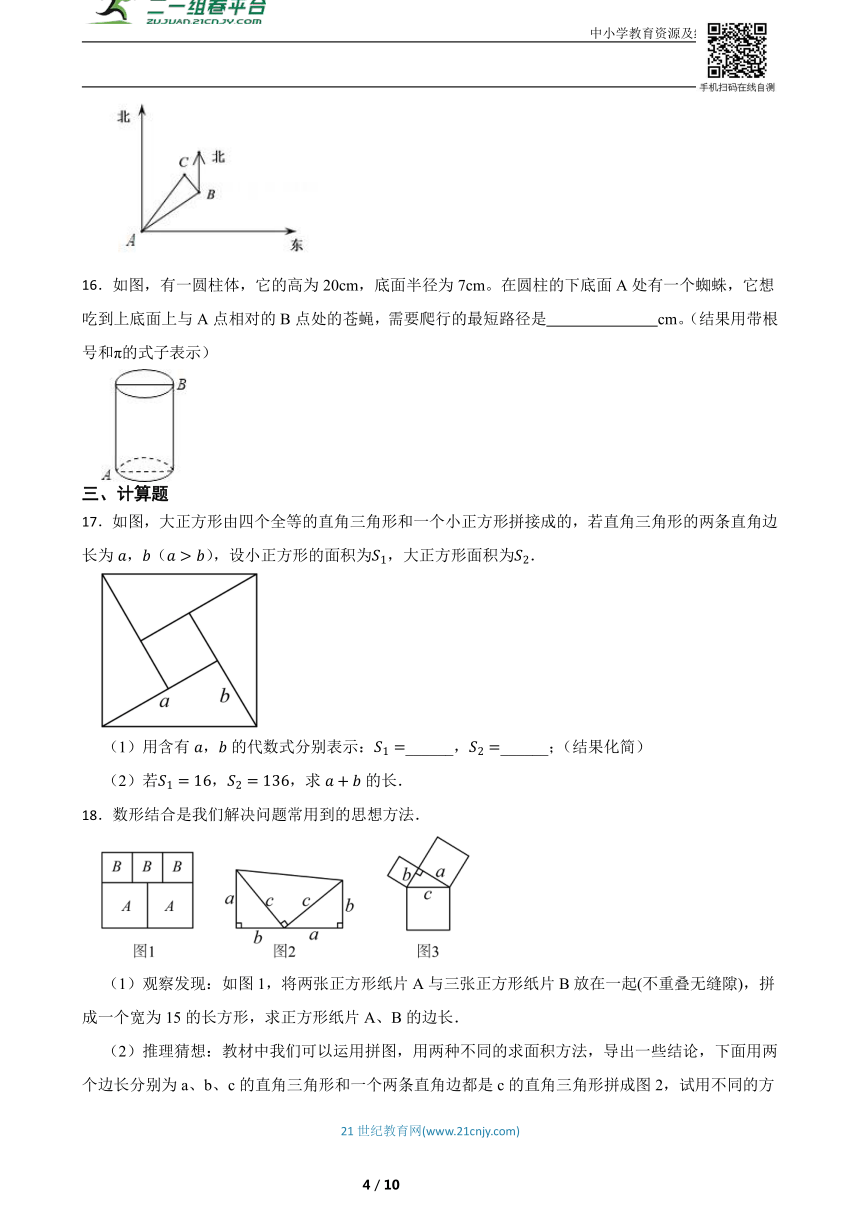
16.如图,有一圆柱体,它的高为20cm,底面半径为7cm。在圆柱的下底面A处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是 cm。(结果用带根号和π的式子表示)
三、计算题
17.如图,大正方形由四个全等的直角三角形和一个小正方形拼接成的,若直角三角形的两条直角边长为,(),设小正方形的面积为,大正方形面积为.
(1)用含有,的代数式分别表示:______,______;(结果化简)
(2)若,,求的长.
18.数形结合是我们解决问题常用到的思想方法.
(1)观察发现:如图1,将两张正方形纸片A与三张正方形纸片B放在一起(不重叠无缝隙),拼成一个宽为15的长方形,求正方形纸片A、B的边长.
(2)推理猜想:教材中我们可以运用拼图,用两种不同的求面积方法,导出一些结论,下面用两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成图2,试用不同的方法计算图2的面积,S=__________________,或者S= ____________________,经化简后,请写出边长为a、b、c的直角三角形三边的关系: ___________________________________.
(3)灵活应用:图3中,以边长a、b 、c的直角三角形三边向外作正方形,若,,则以b为边长作的正方形面积=_______________.
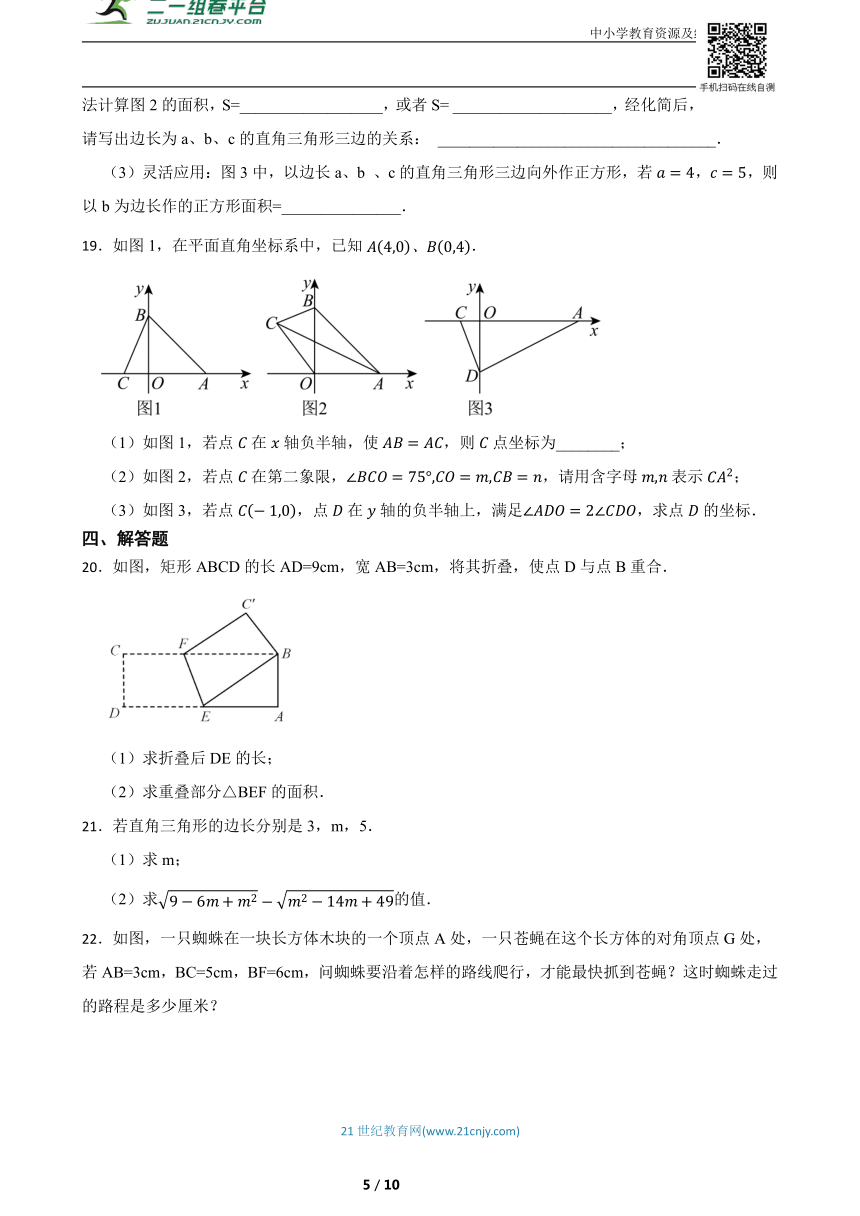
19.如图1,在平面直角坐标系中,已知.
(1)如图1,若点在轴负半轴,使,则点坐标为________;
(2)如图2,若点在第二象限,,请用含字母表示;
(3)如图3,若点,点在轴的负半轴上,满足,求点的坐标.
四、解答题
20.如图,矩形ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合.
(1)求折叠后DE的长;
(2)求重叠部分△BEF的面积.
21.若直角三角形的边长分别是3,m,5.
(1)求m;
(2)求的值.
22.如图,一只蜘蛛在一块长方体木块的一个顶点A处,一只苍蝇在这个长方体的对角顶点G处,若AB=3cm,BC=5cm,BF=6cm,问蜘蛛要沿着怎样的路线爬行,才能最快抓到苍蝇?这时蜘蛛走过的路程是多少厘米?
23.两个顶角相等的等腰三角形.如果具有公共的顶角顶点,把它们的底角顶点连接起来形成一组可证得全等的三角形,我们把连接的那两条线段叫做“友好”线段.例如:如图1,△ABC中,,△ADE中,,且,连接DB,EC,则可证得,此时线段DB和线段EC就是一对“友好”线段.
(1)如图2,△ABC和△CDE都是等腰直角三角形,且.
①图中线段AE的“友好”线段是______;
②连接AD,若,,,求AE的长;
(2)如图3,△ABC是等腰直角三角形,,P是△ACB外一点,,,,求线段BP的长.
答案解析部分
1.【答案】B
【知识点】无理数在数轴上表示;勾股定理
2.【答案】B
【知识点】勾股定理
3.【答案】B
【知识点】直角三角形全等的判定-HL;角平分线的性质;勾股定理
4.【答案】C
【知识点】勾股定理
5.【答案】D
【知识点】勾股定理的逆定理
6.【答案】A
【知识点】无理数的估值;勾股定理的应用
7.【答案】D
【知识点】勾股定理
8.【答案】A
【知识点】勾股定理;勾股定理的逆定理
9.【答案】B
【知识点】直角三角形全等的判定-HL;角平分线的性质;勾股定理
10.【答案】A
【知识点】坐标与图形性质;勾股定理
11.【答案】
【知识点】三角形的面积;勾股定理的逆定理
12.【答案】-
【知识点】无理数在数轴上表示;勾股定理
13.【答案】
【知识点】等边三角形的性质;勾股定理;点的坐标与象限的关系
14.【答案】(0,)
【知识点】点的坐标;勾股定理
15.【答案】北偏西18°
【知识点】钟面角、方位角;勾股定理的逆定理
16.【答案】
【知识点】勾股定理的实际应用-最短路径问题
17.【答案】(1),
(2)
【知识点】完全平方公式的几何背景;勾股定理
18.【答案】(1)9;6
(2);;
(3)9
【知识点】勾股定理;勾股定理的证明;二元一次方程组的应用-几何问题
19.【答案】(1)
(2)
(3)
【知识点】最简二次根式;坐标与图形性质;等腰三角形的判定与性质;勾股定理
20.【答案】(1)折叠后DE的长为5cm;(2)重叠部分△BEF的面积为7.5cm2.
【知识点】勾股定理
21.【答案】(1)或
(2)或
【知识点】二次根式的性质与化简;勾股定理
22.【答案】解:(1)如图(1)当蚂蚁从A出发先到EF上再到点G时∵BC=5cm,∴FG=BC=5cm,∴BG=5+6=11cm在Rt△ABG中AG===,∵>10(2)如图(2)当蚂蚁从A出发先到BF上再到点G时∵AB=3cm,BC=5cm∴AC=AB+BC=3+5=8cm∵BF=6cm,∴CG=BF=6cm在Rt△ABG中AG= = =10cm ∴第一种方案最近,这时蜘蛛走过的路程是10cm.
【知识点】勾股定理的实际应用-最短路径问题
23.【答案】(1)解:①BD;
②如图,连接AD,
∵,
∴.
在△ABC中,,,,
∴,.
∵,
∴,
∴,
∴.
(2)解:如图,以C为直角顶点构造等腰直角三角形PCD,连接AD,过点D作交AP的延长线于点E.
由(1)可得.
在△PCD中,,,
∴.
∵,,
∴.
∵,
∴.
∴,.
在△AED中,,,
∴.
∴.
【知识点】等腰三角形的性质;含30°角的直角三角形;勾股定理;三角形全等的判定-SAS
21世纪教育网(www.21cnjy.com)
2 / 10
第十七章勾股定理
一、单选题
1.如图所示,在数轴上点A所表示的数为a,则a的值为( )
A. B. C. D.
2.如图,长方形门框高为2m,宽为1.5m,现有3块木板,尺寸如下:①号木板长3m,宽2.7m;②号木板长4m,宽2.4m;③号木板长2.8m,宽2.6m.能从这扇门通过的木板是( )
A.① B.② C.③号 D.都不能通过
3.如图,Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD平分∠CAB,交BC于D,DE⊥AB于E,则CD等于( )
A.2cm B.3cm C.4cm D.5cm
4.图中的四边形均为正方形,三角形为直角三角形,最大的正方形的边长为7cm,则图中A、B两个正方形的面积之和为( )
A.28cm2 B.42cm2 C.49cm2 D.63cm2
5.在下列由线段组成的三角形中,是直角三角形的是( )
A.,, B.,,
C.,, D.,,
6.如图,一根长5米的竹竿 斜靠在竖直的墙上,这时 为4米,若竹竿的顶端 沿墙下滑2米至 处,则竹竿底端 外移的距离 ( )
A.小于2米 B.等于2米 C.大于2米 D.以上都不对
7.如果一个直角三角形的两条边长分别为 和 ,那么这个三角形的第三边长为( )
A. B. C. D. 或
8.下列说法中,正确的个数有( )
①如果是直角三角形,那么一定成立;
②在中,如果,那么一定不是直角三角形;
③两角及一边分别相等的两个三角形全等.
A.0 B.1 C.2 D.3
9.如图,Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD平分∠CAB,交BC于D,DE⊥AB于E,则CD等于( )
A.2cm B.3cm C.4cm D.5cm
10.如图,把平面内一条数轴x绕点O逆时针旋转角()得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:已知点P是平面斜坐标系中任意一点,过点P作y轴的平行线交x轴于点A,过点P作x轴的平行线交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对为点P的斜坐标.在平面斜坐标系中,若,点P的斜坐标为,点G的斜坐标为,连接,则线段的长度是( )
A. B. C. D.
二、填空题
11.已知一个三角形的三边长分别为cm、3cm、2cm,则这个三角形的面积为 cm2.
12.如图,在数轴上点A表示实数.
13.如图,在平面直角坐标系中,已知等边三角形ABC的顶点A的坐标是(1,),则点C的坐标是 .
14.如图,,,以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为 .
15.如图,快艇计划从A地到距离A地10海里的C地,先沿北偏东72°方向行驶8海里到达B地,再从B地行驶6海里到达C地,此时快艇位于B地的方向是 .
16.如图,有一圆柱体,它的高为20cm,底面半径为7cm。在圆柱的下底面A处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是 cm。(结果用带根号和π的式子表示)
三、计算题
17.如图,大正方形由四个全等的直角三角形和一个小正方形拼接成的,若直角三角形的两条直角边长为,(),设小正方形的面积为,大正方形面积为.
(1)用含有,的代数式分别表示:______,______;(结果化简)
(2)若,,求的长.
18.数形结合是我们解决问题常用到的思想方法.
(1)观察发现:如图1,将两张正方形纸片A与三张正方形纸片B放在一起(不重叠无缝隙),拼成一个宽为15的长方形,求正方形纸片A、B的边长.
(2)推理猜想:教材中我们可以运用拼图,用两种不同的求面积方法,导出一些结论,下面用两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成图2,试用不同的方法计算图2的面积,S=__________________,或者S= ____________________,经化简后,请写出边长为a、b、c的直角三角形三边的关系: ___________________________________.
(3)灵活应用:图3中,以边长a、b 、c的直角三角形三边向外作正方形,若,,则以b为边长作的正方形面积=_______________.
19.如图1,在平面直角坐标系中,已知.
(1)如图1,若点在轴负半轴,使,则点坐标为________;
(2)如图2,若点在第二象限,,请用含字母表示;
(3)如图3,若点,点在轴的负半轴上,满足,求点的坐标.
四、解答题
20.如图,矩形ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合.
(1)求折叠后DE的长;
(2)求重叠部分△BEF的面积.
21.若直角三角形的边长分别是3,m,5.
(1)求m;
(2)求的值.
22.如图,一只蜘蛛在一块长方体木块的一个顶点A处,一只苍蝇在这个长方体的对角顶点G处,若AB=3cm,BC=5cm,BF=6cm,问蜘蛛要沿着怎样的路线爬行,才能最快抓到苍蝇?这时蜘蛛走过的路程是多少厘米?
23.两个顶角相等的等腰三角形.如果具有公共的顶角顶点,把它们的底角顶点连接起来形成一组可证得全等的三角形,我们把连接的那两条线段叫做“友好”线段.例如:如图1,△ABC中,,△ADE中,,且,连接DB,EC,则可证得,此时线段DB和线段EC就是一对“友好”线段.
(1)如图2,△ABC和△CDE都是等腰直角三角形,且.
①图中线段AE的“友好”线段是______;
②连接AD,若,,,求AE的长;
(2)如图3,△ABC是等腰直角三角形,,P是△ACB外一点,,,,求线段BP的长.
答案解析部分
1.【答案】B
【知识点】无理数在数轴上表示;勾股定理
2.【答案】B
【知识点】勾股定理
3.【答案】B
【知识点】直角三角形全等的判定-HL;角平分线的性质;勾股定理
4.【答案】C
【知识点】勾股定理
5.【答案】D
【知识点】勾股定理的逆定理
6.【答案】A
【知识点】无理数的估值;勾股定理的应用
7.【答案】D
【知识点】勾股定理
8.【答案】A
【知识点】勾股定理;勾股定理的逆定理
9.【答案】B
【知识点】直角三角形全等的判定-HL;角平分线的性质;勾股定理
10.【答案】A
【知识点】坐标与图形性质;勾股定理
11.【答案】
【知识点】三角形的面积;勾股定理的逆定理
12.【答案】-
【知识点】无理数在数轴上表示;勾股定理
13.【答案】
【知识点】等边三角形的性质;勾股定理;点的坐标与象限的关系
14.【答案】(0,)
【知识点】点的坐标;勾股定理
15.【答案】北偏西18°
【知识点】钟面角、方位角;勾股定理的逆定理
16.【答案】
【知识点】勾股定理的实际应用-最短路径问题
17.【答案】(1),
(2)
【知识点】完全平方公式的几何背景;勾股定理
18.【答案】(1)9;6
(2);;
(3)9
【知识点】勾股定理;勾股定理的证明;二元一次方程组的应用-几何问题
19.【答案】(1)
(2)
(3)
【知识点】最简二次根式;坐标与图形性质;等腰三角形的判定与性质;勾股定理
20.【答案】(1)折叠后DE的长为5cm;(2)重叠部分△BEF的面积为7.5cm2.
【知识点】勾股定理
21.【答案】(1)或
(2)或
【知识点】二次根式的性质与化简;勾股定理
22.【答案】解:(1)如图(1)当蚂蚁从A出发先到EF上再到点G时∵BC=5cm,∴FG=BC=5cm,∴BG=5+6=11cm在Rt△ABG中AG===,∵>10(2)如图(2)当蚂蚁从A出发先到BF上再到点G时∵AB=3cm,BC=5cm∴AC=AB+BC=3+5=8cm∵BF=6cm,∴CG=BF=6cm在Rt△ABG中AG= = =10cm ∴第一种方案最近,这时蜘蛛走过的路程是10cm.
【知识点】勾股定理的实际应用-最短路径问题
23.【答案】(1)解:①BD;
②如图,连接AD,
∵,
∴.
在△ABC中,,,,
∴,.
∵,
∴,
∴,
∴.
(2)解:如图,以C为直角顶点构造等腰直角三角形PCD,连接AD,过点D作交AP的延长线于点E.
由(1)可得.
在△PCD中,,,
∴.
∵,,
∴.
∵,
∴.
∴,.
在△AED中,,,
∴.
∴.
【知识点】等腰三角形的性质;含30°角的直角三角形;勾股定理;三角形全等的判定-SAS
21世纪教育网(www.21cnjy.com)
2 / 10
