第十七章 勾股定理【培优】(含答案)
文档属性
| 名称 | 第十七章 勾股定理【培优】(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 506.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-21 16:15:45 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十七章 勾股定理【培优】
一、单选题
1.(2024八上·长春期末)如图,,则数轴上点A所表示的数为( )
A. B. C. D.
2.(2024九上·衢州月考)在中,,若,则的值为( )
A. B. C. D.
3.(2023八下·丘北月考)如图,在中,,,,,是的平分线,则的周长为( )
A.5 B.6 C.7 D.8
4.(2024九上·四会期末)如图,的弦,是的中点,且则的半径等于( )
A. B. C. D.
5.(2024八上·南海月考)下列四组线段中,可以构成直角三角形的是( )
A.4、5、6 B. C.2、3、4 D.
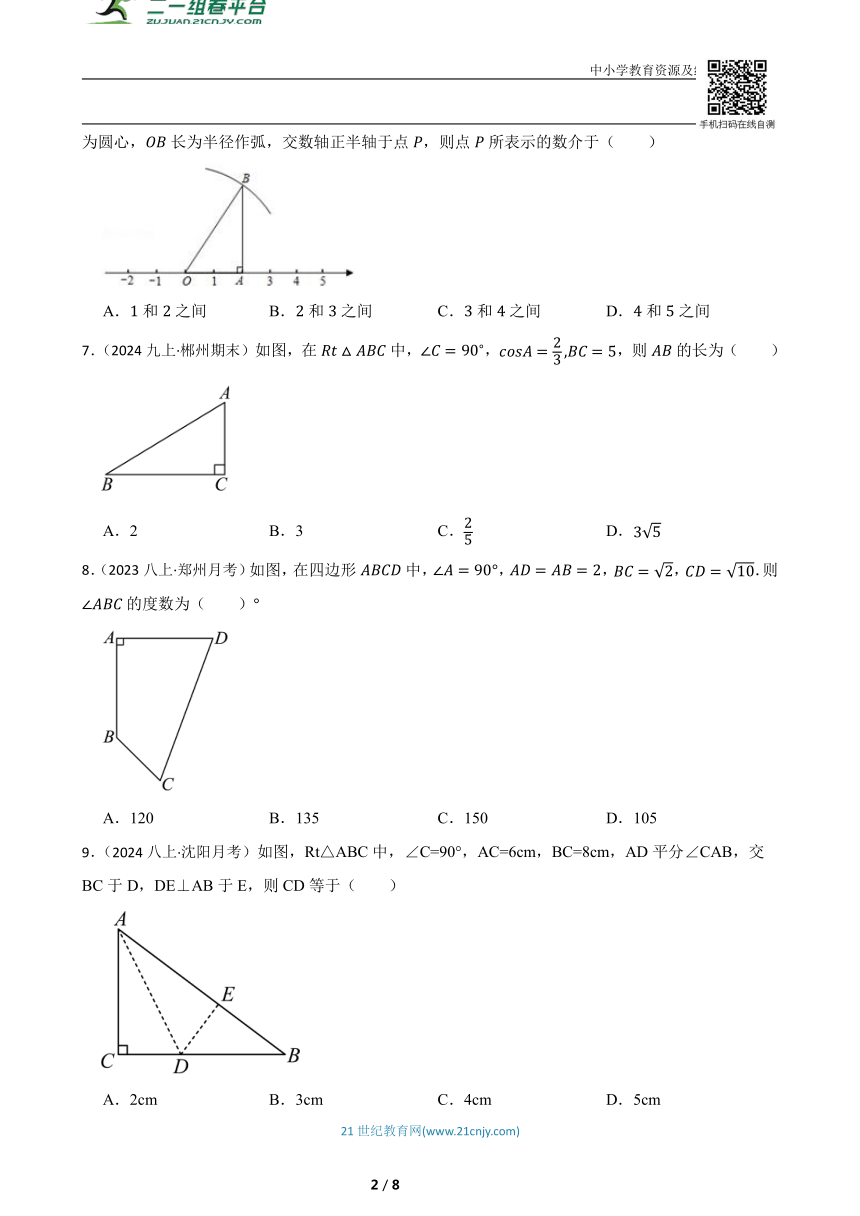
6.(2023八上·市中区月考)如图,小明学了在数轴上画出表示无理数的点的方法后,进行练习:首先画数轴,原点为,在数轴上找到表示数的点,然后过点作,使如图以为圆心,长为半径作弧,交数轴正半轴于点,则点所表示的数介于( )
A.和之间 B.和之间 C.和之间 D.和之间
7.(2024九上·郴州期末)如图,在中,,,则的长为( )
A.2 B.3 C. D.
8.(2023八上·郑州月考)如图,在四边形中,,,,.则的度数为( )
A.120 B.135 C.150 D.105
9.(2024八上·沈阳月考)如图,Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD平分∠CAB,交BC于D,DE⊥AB于E,则CD等于( )
A.2cm B.3cm C.4cm D.5cm
10.(2023九上·镇海区月考)如图,在平面直角坐标系中,与轴相切于原点,平行于轴的直线交于两点,若点的坐标是,则点的坐标为( )
A. B. C. D.
二、填空题
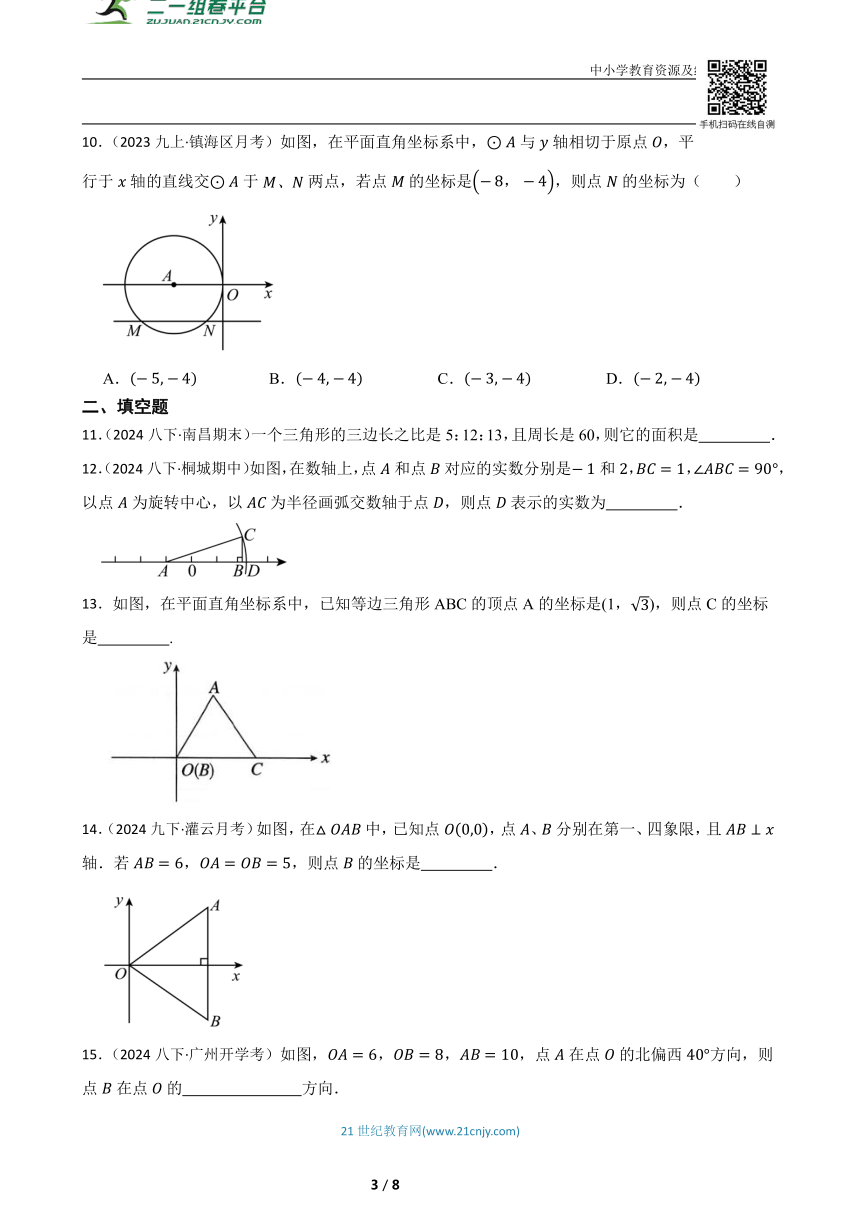
11.(2024八下·南昌期末)一个三角形的三边长之比是5:12:13,且周长是60,则它的面积是 .
12.(2024八下·桐城期中)如图,在数轴上,点和点对应的实数分别是和,,,以点为旋转中心,以为半径画弧交数轴于点,则点表示的实数为 .
13.如图,在平面直角坐标系中,已知等边三角形ABC的顶点A的坐标是(1,),则点C的坐标是 .
14.(2024九下·灌云月考)如图,在中,已知点,点、分别在第一、四象限,且轴.若,,则点的坐标是 .
15.(2024八下·广州开学考)如图,,,,点在点的北偏西方向,则点在点的 方向.
16.(2024八上·成都期中)如图,圆柱体的底面圆周长为16,高为6,是上底面的直径.一只蚂蚁从圆柱的表面点出发,沿着圆柱的侧面爬行到点,则爬行的最短路程为 cm.
三、计算题
17.(2023八上·连江期末)如图,大正方形由四个全等的直角三角形和一个小正方形拼接成的,若直角三角形的两条直角边长为,(),设小正方形的面积为,大正方形面积为.
(1)用含有,的代数式分别表示:______,______;(结果化简)
(2)若,,求的长.
18.(2023八上·大竹期中)数形结合是我们解决问题常用到的思想方法.
(1)观察发现:如图1,将两张正方形纸片A与三张正方形纸片B放在一起(不重叠无缝隙),拼成一个宽为15的长方形,求正方形纸片A、B的边长.
(2)推理猜想:教材中我们可以运用拼图,用两种不同的求面积方法,导出一些结论,下面用两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成图2,试用不同的方法计算图2的面积,S=__________________,或者S= ____________________,经化简后,请写出边长为a、b、c的直角三角形三边的关系: ___________________________________.
(3)灵活应用:图3中,以边长a、b 、c的直角三角形三边向外作正方形,若,,则以b为边长作的正方形面积=_______________.
19.(2024八下·武汉月考)如图1,在平面直角坐标系中,已知.
(1)如图1,若点在轴负半轴,使,则点坐标为________;
(2)如图2,若点在第二象限,,请用含字母表示;
(3)如图3,若点,点在轴的负半轴上,满足,求点的坐标.
四、解答题
20.(2024八下·恩平期中)如图所示,中,,,,
(1)求的长,
(2)求的长.
21.(2023八上·禅城期中)在平面直角坐标系中,已知点为坐标原点,点.是等边三角形,点在第一象限.求点的坐标.
22.(2023八上·尤溪月考)如图,这是一个棱长为1cm的正方体空盒子(盒子表面厚度忽略不计).
(1)盒子外有一只蚂蚁从点A沿表面爬到相对的点B,求蚂蚁爬行的最短路程.
(2)盒子内有一只飞虫从点A飞到相对的点B,求飞虫飞行的最短路程.
23.(2024八上·肇源月考)如图,在中,平分,交边于点D,点E是边的中点.点P为边上的一个动点.
(1) , ;
(2)若是等腰三角形,则的度数为 ;
(3)当四边形为轴对称图形时,求的长;
(4)若点M在线段上,连接,直接写出的值最小时的长度.
答案解析部分
1.【答案】B
【知识点】无理数在数轴上表示;勾股定理
2.【答案】A
【知识点】勾股定理;余弦的概念;求正切值
3.【答案】B
【知识点】直角三角形全等的判定-HL;角平分线的性质;勾股定理
4.【答案】B
【知识点】勾股定理;垂径定理
5.【答案】D
【知识点】勾股定理的逆定理
6.【答案】C
【知识点】无理数的估值;勾股定理的应用
7.【答案】D
【知识点】勾股定理;解直角三角形
8.【答案】B
【知识点】勾股定理;勾股定理的逆定理
9.【答案】B
【知识点】直角三角形全等的判定-HL;角平分线的性质;勾股定理
10.【答案】D
【知识点】坐标与图形性质;勾股定理;垂径定理;切线的性质
11.【答案】120
【知识点】三角形的面积;勾股定理的逆定理
12.【答案】
【知识点】无理数在数轴上表示;勾股定理;数轴上两点之间的距离
13.【答案】
【知识点】等边三角形的性质;勾股定理;点的坐标与象限的关系
14.【答案】
【知识点】点的坐标;等腰三角形的判定与性质;勾股定理
15.【答案】北偏东50°
【知识点】钟面角、方位角;勾股定理的逆定理
16.【答案】10
【知识点】勾股定理;勾股定理的实际应用-最短路径问题
17.【答案】(1),
(2)
【知识点】完全平方公式的几何背景;勾股定理
18.【答案】(1)9;6
(2);;
(3)9
【知识点】勾股定理;勾股定理的证明;二元一次方程组的应用-几何问题
19.【答案】(1)
(2)
(3)
【知识点】最简二次根式;坐标与图形性质;等腰三角形的判定与性质;勾股定理
20.【答案】(1)
(2)
【知识点】等腰三角形的判定与性质;含30°角的直角三角形;勾股定理
21.【答案】
【知识点】二次根式的性质与化简;坐标与图形性质;等边三角形的性质;勾股定理
22.【答案】(1)
(2)
【知识点】勾股定理的实际应用-最短路径问题
23.【答案】(1);
(2)的度数为或或;
(3);
(4).
【知识点】等腰三角形的性质;含30°角的直角三角形;勾股定理;三角形全等的判定-SAS
21世纪教育网(www.21cnjy.com)
2 / 8
第十七章 勾股定理【培优】
一、单选题
1.(2024八上·长春期末)如图,,则数轴上点A所表示的数为( )
A. B. C. D.
2.(2024九上·衢州月考)在中,,若,则的值为( )
A. B. C. D.
3.(2023八下·丘北月考)如图,在中,,,,,是的平分线,则的周长为( )
A.5 B.6 C.7 D.8
4.(2024九上·四会期末)如图,的弦,是的中点,且则的半径等于( )
A. B. C. D.
5.(2024八上·南海月考)下列四组线段中,可以构成直角三角形的是( )
A.4、5、6 B. C.2、3、4 D.
6.(2023八上·市中区月考)如图,小明学了在数轴上画出表示无理数的点的方法后,进行练习:首先画数轴,原点为,在数轴上找到表示数的点,然后过点作,使如图以为圆心,长为半径作弧,交数轴正半轴于点,则点所表示的数介于( )
A.和之间 B.和之间 C.和之间 D.和之间
7.(2024九上·郴州期末)如图,在中,,,则的长为( )
A.2 B.3 C. D.
8.(2023八上·郑州月考)如图,在四边形中,,,,.则的度数为( )
A.120 B.135 C.150 D.105
9.(2024八上·沈阳月考)如图,Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD平分∠CAB,交BC于D,DE⊥AB于E,则CD等于( )
A.2cm B.3cm C.4cm D.5cm
10.(2023九上·镇海区月考)如图,在平面直角坐标系中,与轴相切于原点,平行于轴的直线交于两点,若点的坐标是,则点的坐标为( )
A. B. C. D.
二、填空题
11.(2024八下·南昌期末)一个三角形的三边长之比是5:12:13,且周长是60,则它的面积是 .
12.(2024八下·桐城期中)如图,在数轴上,点和点对应的实数分别是和,,,以点为旋转中心,以为半径画弧交数轴于点,则点表示的实数为 .
13.如图,在平面直角坐标系中,已知等边三角形ABC的顶点A的坐标是(1,),则点C的坐标是 .
14.(2024九下·灌云月考)如图,在中,已知点,点、分别在第一、四象限,且轴.若,,则点的坐标是 .
15.(2024八下·广州开学考)如图,,,,点在点的北偏西方向,则点在点的 方向.
16.(2024八上·成都期中)如图,圆柱体的底面圆周长为16,高为6,是上底面的直径.一只蚂蚁从圆柱的表面点出发,沿着圆柱的侧面爬行到点,则爬行的最短路程为 cm.
三、计算题
17.(2023八上·连江期末)如图,大正方形由四个全等的直角三角形和一个小正方形拼接成的,若直角三角形的两条直角边长为,(),设小正方形的面积为,大正方形面积为.
(1)用含有,的代数式分别表示:______,______;(结果化简)
(2)若,,求的长.
18.(2023八上·大竹期中)数形结合是我们解决问题常用到的思想方法.
(1)观察发现:如图1,将两张正方形纸片A与三张正方形纸片B放在一起(不重叠无缝隙),拼成一个宽为15的长方形,求正方形纸片A、B的边长.
(2)推理猜想:教材中我们可以运用拼图,用两种不同的求面积方法,导出一些结论,下面用两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成图2,试用不同的方法计算图2的面积,S=__________________,或者S= ____________________,经化简后,请写出边长为a、b、c的直角三角形三边的关系: ___________________________________.
(3)灵活应用:图3中,以边长a、b 、c的直角三角形三边向外作正方形,若,,则以b为边长作的正方形面积=_______________.
19.(2024八下·武汉月考)如图1,在平面直角坐标系中,已知.
(1)如图1,若点在轴负半轴,使,则点坐标为________;
(2)如图2,若点在第二象限,,请用含字母表示;
(3)如图3,若点,点在轴的负半轴上,满足,求点的坐标.
四、解答题
20.(2024八下·恩平期中)如图所示,中,,,,
(1)求的长,
(2)求的长.
21.(2023八上·禅城期中)在平面直角坐标系中,已知点为坐标原点,点.是等边三角形,点在第一象限.求点的坐标.
22.(2023八上·尤溪月考)如图,这是一个棱长为1cm的正方体空盒子(盒子表面厚度忽略不计).
(1)盒子外有一只蚂蚁从点A沿表面爬到相对的点B,求蚂蚁爬行的最短路程.
(2)盒子内有一只飞虫从点A飞到相对的点B,求飞虫飞行的最短路程.
23.(2024八上·肇源月考)如图,在中,平分,交边于点D,点E是边的中点.点P为边上的一个动点.
(1) , ;
(2)若是等腰三角形,则的度数为 ;
(3)当四边形为轴对称图形时,求的长;
(4)若点M在线段上,连接,直接写出的值最小时的长度.
答案解析部分
1.【答案】B
【知识点】无理数在数轴上表示;勾股定理
2.【答案】A
【知识点】勾股定理;余弦的概念;求正切值
3.【答案】B
【知识点】直角三角形全等的判定-HL;角平分线的性质;勾股定理
4.【答案】B
【知识点】勾股定理;垂径定理
5.【答案】D
【知识点】勾股定理的逆定理
6.【答案】C
【知识点】无理数的估值;勾股定理的应用
7.【答案】D
【知识点】勾股定理;解直角三角形
8.【答案】B
【知识点】勾股定理;勾股定理的逆定理
9.【答案】B
【知识点】直角三角形全等的判定-HL;角平分线的性质;勾股定理
10.【答案】D
【知识点】坐标与图形性质;勾股定理;垂径定理;切线的性质
11.【答案】120
【知识点】三角形的面积;勾股定理的逆定理
12.【答案】
【知识点】无理数在数轴上表示;勾股定理;数轴上两点之间的距离
13.【答案】
【知识点】等边三角形的性质;勾股定理;点的坐标与象限的关系
14.【答案】
【知识点】点的坐标;等腰三角形的判定与性质;勾股定理
15.【答案】北偏东50°
【知识点】钟面角、方位角;勾股定理的逆定理
16.【答案】10
【知识点】勾股定理;勾股定理的实际应用-最短路径问题
17.【答案】(1),
(2)
【知识点】完全平方公式的几何背景;勾股定理
18.【答案】(1)9;6
(2);;
(3)9
【知识点】勾股定理;勾股定理的证明;二元一次方程组的应用-几何问题
19.【答案】(1)
(2)
(3)
【知识点】最简二次根式;坐标与图形性质;等腰三角形的判定与性质;勾股定理
20.【答案】(1)
(2)
【知识点】等腰三角形的判定与性质;含30°角的直角三角形;勾股定理
21.【答案】
【知识点】二次根式的性质与化简;坐标与图形性质;等边三角形的性质;勾股定理
22.【答案】(1)
(2)
【知识点】勾股定理的实际应用-最短路径问题
23.【答案】(1);
(2)的度数为或或;
(3);
(4).
【知识点】等腰三角形的性质;含30°角的直角三角形;勾股定理;三角形全等的判定-SAS
21世纪教育网(www.21cnjy.com)
2 / 8
