18.1.1平行四边形的性质(含答案)
文档属性
| 名称 | 18.1.1平行四边形的性质(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 449.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-21 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
18.1.1平行四边形的性质
一、单选题
1.如图, 在 , 过点 作 , 垂足为 , 过点 作 , 垂足为E. 若 , 则 的长为( )
A.4 B.3 C. D.2
2.下列命题中,逆命题不成立的是( )
A.等腰三角形的两个底角相等
B.对顶角相等
C.三边对应相等的两个三角形全等
D.对角线互相平分的四边形是平行四边形
3.如图所示,平行四边形中,,则边的长可以是( )
A.2cm B.4cm C.6cm D.8cm
4.如图,四边形是平行四边形,点在边上,,,垂足分别为、,则平行线与之间的距离是( )
A.的长 B.的长 C.的长 D.的长
5.如图,若将四根木条钉成的矩形木框变形为平行四边形 的形状,并使得其面积变为原矩形面积的一半,则平行四边形 的内角 的大小为( )
A.100° B.120° C.135° D.150°
二、填空题
6.如图,在平行四边形中,,的平分线,分别与相交于点E,F,若,,则的长为.
7.如图, ABCD的一个外角∠CBE是70°,则∠D的大小是 .
8.如图,平行四边形的顶点A,B在函数的图象上,边与y轴交于点D,轴于点E.若的面积为8,则的值为 .
9.在平行四边形ABCD中∠A=120°,则∠C的度数为 ;
10.平行四边形中,有两个内角的比为,则这个平行四边形中较小的内角是 .
11.在中,若,则的度数为 度.
三、计算题
12.如图,E、F是平行四边形ABCD对角线AC上的两点,BE∥DF.求证:BE=DF.
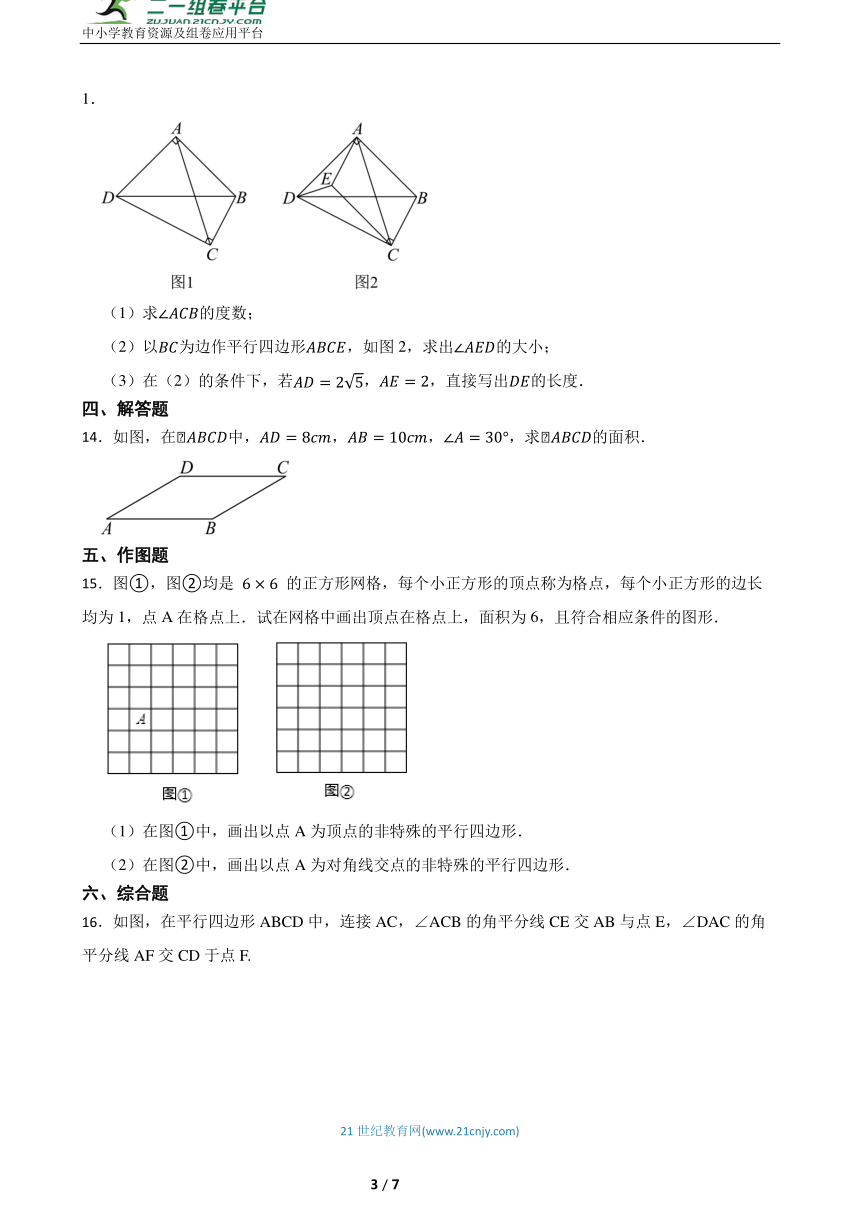
13.已知,在四边形中,点,位于线段的异侧,,,如图1.
(1)求的度数;
(2)以为边作平行四边形,如图2,求出的大小;
(3)在(2)的条件下,若,,直接写出的长度.
四、解答题
14.如图,在中,,,,求的面积.
五、作图题
15.图①,图②均是 的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A在格点上.试在网格中画出顶点在格点上,面积为6,且符合相应条件的图形.
(1)在图①中,画出以点A为顶点的非特殊的平行四边形.
(2)在图②中,画出以点A为对角线交点的非特殊的平行四边形.
六、综合题
16.如图,在平行四边形ABCD中,连接AC,∠ACB的角平分线CE交AB与点E,∠DAC的角平分线AF交CD于点F.
(1)如图1,求证:BE=DF;
(2)如图2,过点A作AH⊥BC,∠ACB=2∠BAH,在不添加任何辅助线和字母的情况下,请直接写出与∠BAH互余的角.
17.如图有两棵树,一棵高,一棵高,两树之间相距,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?
18.如图,已知E、F是 ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.
(1)请写出图中全等三角形(不再添加辅助线).
(2)求证:△ABE≌△CDF;
答案解析部分
1.【答案】B
【知识点】平行四边形的性质
2.【答案】B
【知识点】三角形全等及其性质;等腰三角形的性质;平行四边形的性质;真命题与假命题
3.【答案】B
【知识点】三角形三边关系;平行四边形的性质
4.【答案】B
【知识点】平行线之间的距离;平行四边形的性质
5.【答案】D
【知识点】平行四边形的性质
6.【答案】4
【知识点】角平分线的性质;等腰三角形的判定;平行四边形的性质
7.【答案】110°
【知识点】平行四边形的性质
8.【答案】
【知识点】平行四边形的性质
9.【答案】120°
【知识点】平行四边形的性质
10.【答案】60
【知识点】平行四边形的性质
11.【答案】
【知识点】平行四边形的性质
12.【答案】证明:∵四边形ABCD是平行四边形,
∴BC=AD,BC∥AD,
∴∠ACB=∠DAC,
∵BE∥DF,
∴∠BEC=∠AFD,
∴△CBE≌△ADF,
∴BE=DF.
【知识点】平行四边形的性质
13.【答案】(1)
(2)
(3)
【知识点】等腰三角形的判定与性质;勾股定理;平行四边形的性质;三角形全等的判定-SAS
14.【答案】的面积为
【知识点】含30°角的直角三角形;平行四边形的性质
15.【答案】(1)解:如图,平行四边形ABCD即为所求.
(2)解:如图,平行四边形EFGH即为所求.
【知识点】平行四边形的性质
16.【答案】(1)证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∴∠DAC=∠ACB
∵AF平分∠DAC,∠DAF=∠DAC,
∵CE平分∠ACB,∠ECB-∠ACB,∠DAF=∠ECB
∵四边形ABCD为平行四边形,∠B=∠D
在中
(2)∠ABC,∠BAC,∠ACD,∠ADC,∠HAF.
【知识点】平行四边形的性质
17.【答案】一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了13米
【知识点】平行线之间的距离;勾股定理的应用
18.【答案】(1)解:①△ABC≌△CDA(SSS);②△BCE≌△DAF(SAS);③△ABE≌△CDF(SAS);
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠FCD,
又∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°,
∴△ABE≌△CDF(AAS).
【知识点】三角形全等的判定;平行四边形的性质
21世纪教育网(www.21cnjy.com)
2 / 7
18.1.1平行四边形的性质
一、单选题
1.如图, 在 , 过点 作 , 垂足为 , 过点 作 , 垂足为E. 若 , 则 的长为( )
A.4 B.3 C. D.2
2.下列命题中,逆命题不成立的是( )
A.等腰三角形的两个底角相等
B.对顶角相等
C.三边对应相等的两个三角形全等
D.对角线互相平分的四边形是平行四边形
3.如图所示,平行四边形中,,则边的长可以是( )
A.2cm B.4cm C.6cm D.8cm
4.如图,四边形是平行四边形,点在边上,,,垂足分别为、,则平行线与之间的距离是( )
A.的长 B.的长 C.的长 D.的长
5.如图,若将四根木条钉成的矩形木框变形为平行四边形 的形状,并使得其面积变为原矩形面积的一半,则平行四边形 的内角 的大小为( )
A.100° B.120° C.135° D.150°
二、填空题
6.如图,在平行四边形中,,的平分线,分别与相交于点E,F,若,,则的长为.
7.如图, ABCD的一个外角∠CBE是70°,则∠D的大小是 .
8.如图,平行四边形的顶点A,B在函数的图象上,边与y轴交于点D,轴于点E.若的面积为8,则的值为 .
9.在平行四边形ABCD中∠A=120°,则∠C的度数为 ;
10.平行四边形中,有两个内角的比为,则这个平行四边形中较小的内角是 .
11.在中,若,则的度数为 度.
三、计算题
12.如图,E、F是平行四边形ABCD对角线AC上的两点,BE∥DF.求证:BE=DF.
13.已知,在四边形中,点,位于线段的异侧,,,如图1.
(1)求的度数;
(2)以为边作平行四边形,如图2,求出的大小;
(3)在(2)的条件下,若,,直接写出的长度.
四、解答题
14.如图,在中,,,,求的面积.
五、作图题
15.图①,图②均是 的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A在格点上.试在网格中画出顶点在格点上,面积为6,且符合相应条件的图形.
(1)在图①中,画出以点A为顶点的非特殊的平行四边形.
(2)在图②中,画出以点A为对角线交点的非特殊的平行四边形.
六、综合题
16.如图,在平行四边形ABCD中,连接AC,∠ACB的角平分线CE交AB与点E,∠DAC的角平分线AF交CD于点F.
(1)如图1,求证:BE=DF;
(2)如图2,过点A作AH⊥BC,∠ACB=2∠BAH,在不添加任何辅助线和字母的情况下,请直接写出与∠BAH互余的角.
17.如图有两棵树,一棵高,一棵高,两树之间相距,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?
18.如图,已知E、F是 ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.
(1)请写出图中全等三角形(不再添加辅助线).
(2)求证:△ABE≌△CDF;
答案解析部分
1.【答案】B
【知识点】平行四边形的性质
2.【答案】B
【知识点】三角形全等及其性质;等腰三角形的性质;平行四边形的性质;真命题与假命题
3.【答案】B
【知识点】三角形三边关系;平行四边形的性质
4.【答案】B
【知识点】平行线之间的距离;平行四边形的性质
5.【答案】D
【知识点】平行四边形的性质
6.【答案】4
【知识点】角平分线的性质;等腰三角形的判定;平行四边形的性质
7.【答案】110°
【知识点】平行四边形的性质
8.【答案】
【知识点】平行四边形的性质
9.【答案】120°
【知识点】平行四边形的性质
10.【答案】60
【知识点】平行四边形的性质
11.【答案】
【知识点】平行四边形的性质
12.【答案】证明:∵四边形ABCD是平行四边形,
∴BC=AD,BC∥AD,
∴∠ACB=∠DAC,
∵BE∥DF,
∴∠BEC=∠AFD,
∴△CBE≌△ADF,
∴BE=DF.
【知识点】平行四边形的性质
13.【答案】(1)
(2)
(3)
【知识点】等腰三角形的判定与性质;勾股定理;平行四边形的性质;三角形全等的判定-SAS
14.【答案】的面积为
【知识点】含30°角的直角三角形;平行四边形的性质
15.【答案】(1)解:如图,平行四边形ABCD即为所求.
(2)解:如图,平行四边形EFGH即为所求.
【知识点】平行四边形的性质
16.【答案】(1)证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∴∠DAC=∠ACB
∵AF平分∠DAC,∠DAF=∠DAC,
∵CE平分∠ACB,∠ECB-∠ACB,∠DAF=∠ECB
∵四边形ABCD为平行四边形,∠B=∠D
在中
(2)∠ABC,∠BAC,∠ACD,∠ADC,∠HAF.
【知识点】平行四边形的性质
17.【答案】一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了13米
【知识点】平行线之间的距离;勾股定理的应用
18.【答案】(1)解:①△ABC≌△CDA(SSS);②△BCE≌△DAF(SAS);③△ABE≌△CDF(SAS);
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠FCD,
又∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°,
∴△ABE≌△CDF(AAS).
【知识点】三角形全等的判定;平行四边形的性质
21世纪教育网(www.21cnjy.com)
2 / 7
