18.2.2菱形(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
18.2.2菱形
一、单选题
1.菱形不一定具有的性质是( )
A.四条边相等 B.对角线相等
C.是轴对称图形 D.是中心对称图形
2.如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中点B坐标是(4,1),点D坐标是(0,1),点A在x轴上,则菱形ABCD的周长是( )
A.8 B.2 C.4 D.12
3.如图,在菱形 中,对角线 、 交于点 .若 , ,则 的长为( )
A.1 B. C.2 D.
4.菱形具有而矩形不一定具有的性质是( )
A.对角线互相平分 B.对角线相等
C.邻边互相垂直 D.对角线互相垂直
5.下列条件中,能判定一个四边形为菱形的条件是( )
A.对角线互相平分的四边形
B.对角线互相垂直且平分的四边形
C.对角线相等的四边形
D.对角线相等且互相垂直的四边形
二、填空题
6.如图,在菱形ABCD中,AC=24,BD=10,AC、BD相交于点O,若CE//BD,BE//AC,连接OE,则OE的长是 .
7.一个菱形的两条对角线长分别为3cm,4cm,这个菱形的面积S= .
8.已知菱形 的边长为4, ,则菱形 的面积为 .
9.如图,在矩形中,,连接,分别以点A和点C为圆心,大于一半的长为半径作圆弧,两弧相交于点M和点N,直线分别交于点E、F,连接.给出下面四个结论:①;②四边形是菱形;③;④.上述结论中,所有正确结论的序号是 .
10.如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的边长为 .
11.菱形的两条对角线的长分别是和,则菱形的面积是 .
三、计算题
12.如图,已知在矩形ABCD中,AB=6,BC=2,点E,F分别在边CD,AB上,且DE=BF.
(1)求证:四边形AFCE是平行四边形;
(2)若 AFCE是菱形,求菱形AFCE的边长.
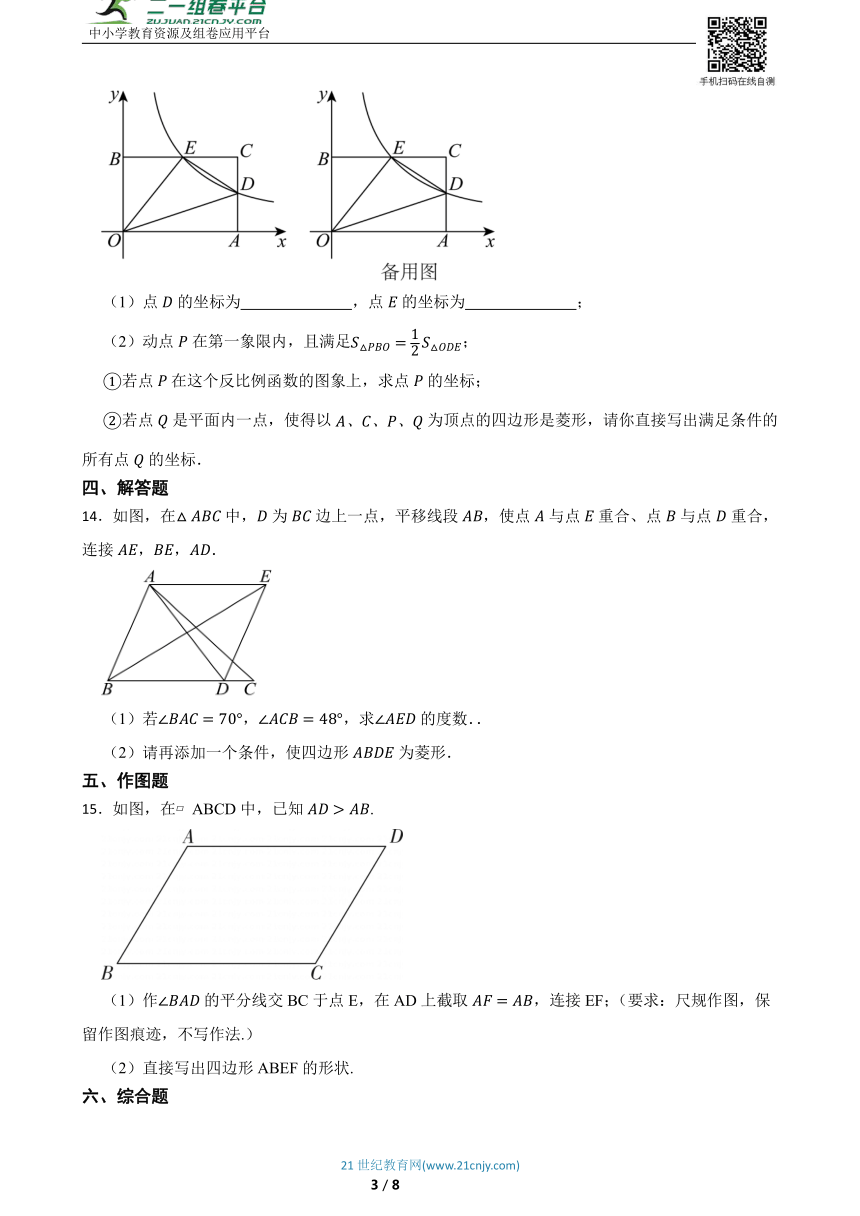
13.如图,在平面直角坐标系中,,是矩形的两个顶点,双曲线经过的中点,点是矩形与双曲线的另一个交点.
(1)点的坐标为 ,点的坐标为 ;
(2)动点在第一象限内,且满足;
若点在这个反比例函数的图象上,求点的坐标;
若点是平面内一点,使得以为顶点的四边形是菱形,请你直接写出满足条件的所有点的坐标.
四、解答题
14.如图,在中,为边上一点,平移线段,使点与点重合、点与点重合,连接,,.
(1)若,,求的度数..
(2)请再添加一个条件,使四边形为菱形.
五、作图题
15.如图,在 ABCD中,已知.
(1)作的平分线交BC于点E,在AD上截取,连接EF;(要求:尺规作图,保留作图痕迹,不写作法.)
(2)直接写出四边形ABEF的形状.
六、综合题
16.已知点、分别是平行四边形的边、的中点.
(1)求证:四边形是平行四边形;
(2)若,,求平行四边形的周长.
17.如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.
(1)求证:AE=BF;
(2)若点E恰好是AD的中点,AB=2,求BD的值.
18.如图,四边形 是菱形,对角线 , 相交于点 ,且 .
(1)求菱形 的周长;
(2)若 ,求 的长.
七、实践探究题
19.小惠自编一题: “如图, 在四边形 中, 对角线 交于点 . 求证: 四边形 是菱形”,并将自己的证明过程与同学小洁交流.
小惠: 小洁:
证明: , 这个题目还缺少条件, 需要补充一个条件才 能证明.
垂直平分 .
,
四边形 是菱形.
若赞同小惠的证法,请在第一个方框内打 “ √ ”;若赞成小洁的说法, 请你补充一个条件, 并证明.
答案解析部分
1.【答案】B
【知识点】菱形的性质
2.【答案】C
【知识点】勾股定理的应用;菱形的性质
3.【答案】C
【知识点】含30°角的直角三角形;菱形的性质
4.【答案】D
【知识点】菱形的性质;矩形的性质
5.【答案】B
【知识点】菱形的判定
6.【答案】13
【知识点】勾股定理;菱形的性质;矩形的判定与性质
7.【答案】6
【知识点】菱形的性质
8.【答案】8
【知识点】含30°角的直角三角形;菱形的性质
9.【答案】①②④
【知识点】线段垂直平分线的性质;菱形的判定与性质;矩形的性质;尺规作图-垂直平分线
10.【答案】6
【知识点】菱形的性质;三角形的中位线定理
11.【答案】9
【知识点】菱形的性质
12.【答案】(1)证明:∵矩形ABCD,
∴DC∥AB,DC=AB,
∵DE=BF,
∴DC-DE=AB-BF即EC=AF,
∴四边形AFCE是平行四边形.
(2)解:∵四边形AFCE是菱形,
∴AF=FC
设AF=FC=x,则BF=6-x,
在Rt△BCF中,
FC2=BC2+BC2
∴x2=22+(6-x)2
解之:x=
答:菱形AFCE的边长为.
【知识点】平行四边形的判定;菱形的性质;矩形的性质
13.【答案】(1),;
(2);或或或.
【知识点】勾股定理;菱形的性质;矩形的性质
14.【答案】(1)
(2),(答案不唯一)
【知识点】三角形内角和定理;平行四边形的判定与性质;菱形的判定
15.【答案】(1)解:如图所示.
(2)解:四边形ABEF是菱形.
【知识点】菱形的判定;尺规作图-作角的平分线
16.【答案】(1)证明:四边形是平行四边形,
,
点、分别是平行四边形的边、的中点,
,,
,
又,四边形是平行四边形;
(2)解:,,是的中点.
,
四边形是平行四边形,
平行四边形是菱形,
平行四边形的周长.
【知识点】平行四边形的判定与性质;菱形的判定与性质
17.【答案】(1)证明:四边形ABCD是菱形
∴AB=BC,AD∥BC
∴∠A=∠CBF
∵BE⊥AD、CF⊥AB
∴∠AEB=∠BFC=90°
∴△AEB≌△BFC(AAS)
∴AE=BF
(2)解:∵E是AD中点,且BE⊥AD
∴直线BE为AD的垂直平分线
∴BD=AB=2
【知识点】线段垂直平分线的性质;菱形的性质
18.【答案】(1)解:∵四边形ABCD是菱形,AB=2,∴菱形ABCD的周长为:8
(2)解:∵四边形ABCD是菱形,AC=2,AB=2
∴AC⊥BD,AO=1,∴BO ,∴BD=2
【知识点】勾股定理;菱形的性质
19.【答案】解:赞成小洁的说法, 补充条件: ,
证明如下:
,
四边形ABCD是平行四边形.
又
∴ 平行四边形 是菱形.
【知识点】菱形的判定
21世纪教育网(www.21cnjy.com)
2 / 8
18.2.2菱形
一、单选题
1.菱形不一定具有的性质是( )
A.四条边相等 B.对角线相等
C.是轴对称图形 D.是中心对称图形
2.如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中点B坐标是(4,1),点D坐标是(0,1),点A在x轴上,则菱形ABCD的周长是( )
A.8 B.2 C.4 D.12
3.如图,在菱形 中,对角线 、 交于点 .若 , ,则 的长为( )
A.1 B. C.2 D.
4.菱形具有而矩形不一定具有的性质是( )
A.对角线互相平分 B.对角线相等
C.邻边互相垂直 D.对角线互相垂直
5.下列条件中,能判定一个四边形为菱形的条件是( )
A.对角线互相平分的四边形
B.对角线互相垂直且平分的四边形
C.对角线相等的四边形
D.对角线相等且互相垂直的四边形
二、填空题
6.如图,在菱形ABCD中,AC=24,BD=10,AC、BD相交于点O,若CE//BD,BE//AC,连接OE,则OE的长是 .
7.一个菱形的两条对角线长分别为3cm,4cm,这个菱形的面积S= .
8.已知菱形 的边长为4, ,则菱形 的面积为 .
9.如图,在矩形中,,连接,分别以点A和点C为圆心,大于一半的长为半径作圆弧,两弧相交于点M和点N,直线分别交于点E、F,连接.给出下面四个结论:①;②四边形是菱形;③;④.上述结论中,所有正确结论的序号是 .
10.如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的边长为 .
11.菱形的两条对角线的长分别是和,则菱形的面积是 .
三、计算题
12.如图,已知在矩形ABCD中,AB=6,BC=2,点E,F分别在边CD,AB上,且DE=BF.
(1)求证:四边形AFCE是平行四边形;
(2)若 AFCE是菱形,求菱形AFCE的边长.
13.如图,在平面直角坐标系中,,是矩形的两个顶点,双曲线经过的中点,点是矩形与双曲线的另一个交点.
(1)点的坐标为 ,点的坐标为 ;
(2)动点在第一象限内,且满足;
若点在这个反比例函数的图象上,求点的坐标;
若点是平面内一点,使得以为顶点的四边形是菱形,请你直接写出满足条件的所有点的坐标.
四、解答题
14.如图,在中,为边上一点,平移线段,使点与点重合、点与点重合,连接,,.
(1)若,,求的度数..
(2)请再添加一个条件,使四边形为菱形.
五、作图题
15.如图,在 ABCD中,已知.
(1)作的平分线交BC于点E,在AD上截取,连接EF;(要求:尺规作图,保留作图痕迹,不写作法.)
(2)直接写出四边形ABEF的形状.
六、综合题
16.已知点、分别是平行四边形的边、的中点.
(1)求证:四边形是平行四边形;
(2)若,,求平行四边形的周长.
17.如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.
(1)求证:AE=BF;
(2)若点E恰好是AD的中点,AB=2,求BD的值.
18.如图,四边形 是菱形,对角线 , 相交于点 ,且 .
(1)求菱形 的周长;
(2)若 ,求 的长.
七、实践探究题
19.小惠自编一题: “如图, 在四边形 中, 对角线 交于点 . 求证: 四边形 是菱形”,并将自己的证明过程与同学小洁交流.
小惠: 小洁:
证明: , 这个题目还缺少条件, 需要补充一个条件才 能证明.
垂直平分 .
,
四边形 是菱形.
若赞同小惠的证法,请在第一个方框内打 “ √ ”;若赞成小洁的说法, 请你补充一个条件, 并证明.
答案解析部分
1.【答案】B
【知识点】菱形的性质
2.【答案】C
【知识点】勾股定理的应用;菱形的性质
3.【答案】C
【知识点】含30°角的直角三角形;菱形的性质
4.【答案】D
【知识点】菱形的性质;矩形的性质
5.【答案】B
【知识点】菱形的判定
6.【答案】13
【知识点】勾股定理;菱形的性质;矩形的判定与性质
7.【答案】6
【知识点】菱形的性质
8.【答案】8
【知识点】含30°角的直角三角形;菱形的性质
9.【答案】①②④
【知识点】线段垂直平分线的性质;菱形的判定与性质;矩形的性质;尺规作图-垂直平分线
10.【答案】6
【知识点】菱形的性质;三角形的中位线定理
11.【答案】9
【知识点】菱形的性质
12.【答案】(1)证明:∵矩形ABCD,
∴DC∥AB,DC=AB,
∵DE=BF,
∴DC-DE=AB-BF即EC=AF,
∴四边形AFCE是平行四边形.
(2)解:∵四边形AFCE是菱形,
∴AF=FC
设AF=FC=x,则BF=6-x,
在Rt△BCF中,
FC2=BC2+BC2
∴x2=22+(6-x)2
解之:x=
答:菱形AFCE的边长为.
【知识点】平行四边形的判定;菱形的性质;矩形的性质
13.【答案】(1),;
(2);或或或.
【知识点】勾股定理;菱形的性质;矩形的性质
14.【答案】(1)
(2),(答案不唯一)
【知识点】三角形内角和定理;平行四边形的判定与性质;菱形的判定
15.【答案】(1)解:如图所示.
(2)解:四边形ABEF是菱形.
【知识点】菱形的判定;尺规作图-作角的平分线
16.【答案】(1)证明:四边形是平行四边形,
,
点、分别是平行四边形的边、的中点,
,,
,
又,四边形是平行四边形;
(2)解:,,是的中点.
,
四边形是平行四边形,
平行四边形是菱形,
平行四边形的周长.
【知识点】平行四边形的判定与性质;菱形的判定与性质
17.【答案】(1)证明:四边形ABCD是菱形
∴AB=BC,AD∥BC
∴∠A=∠CBF
∵BE⊥AD、CF⊥AB
∴∠AEB=∠BFC=90°
∴△AEB≌△BFC(AAS)
∴AE=BF
(2)解:∵E是AD中点,且BE⊥AD
∴直线BE为AD的垂直平分线
∴BD=AB=2
【知识点】线段垂直平分线的性质;菱形的性质
18.【答案】(1)解:∵四边形ABCD是菱形,AB=2,∴菱形ABCD的周长为:8
(2)解:∵四边形ABCD是菱形,AC=2,AB=2
∴AC⊥BD,AO=1,∴BO ,∴BD=2
【知识点】勾股定理;菱形的性质
19.【答案】解:赞成小洁的说法, 补充条件: ,
证明如下:
,
四边形ABCD是平行四边形.
又
∴ 平行四边形 是菱形.
【知识点】菱形的判定
21世纪教育网(www.21cnjy.com)
2 / 8
