18.2.3正方形(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
18.2.3正方形
一、单选题
1.如图,在菱形中,对角线交于点,添加下列一个条件,能使菱形成为正方形的是( )
A. B. C. D.
2.如图,正方形ABCD外侧作等边三角形ADE,则∠AEB的度数为( )
A.30° B.20° C.15° D.10°
3.正方形 菱形 矩形都具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.对角线平分一组对角
4.下列说法中正确的是( )
A.两条对角线垂直的四边形是菱形
B.对角线垂直且相等的四边形是正方形
C.两条对角线相等的四边形是矩形
D.两条对角线相等的平行四边形是矩形
5.如图,在正方形 中, 是 的中点,点 在 上,且 .则 的面积是( )
A.5 B.6 C.7 D.8
二、填空题
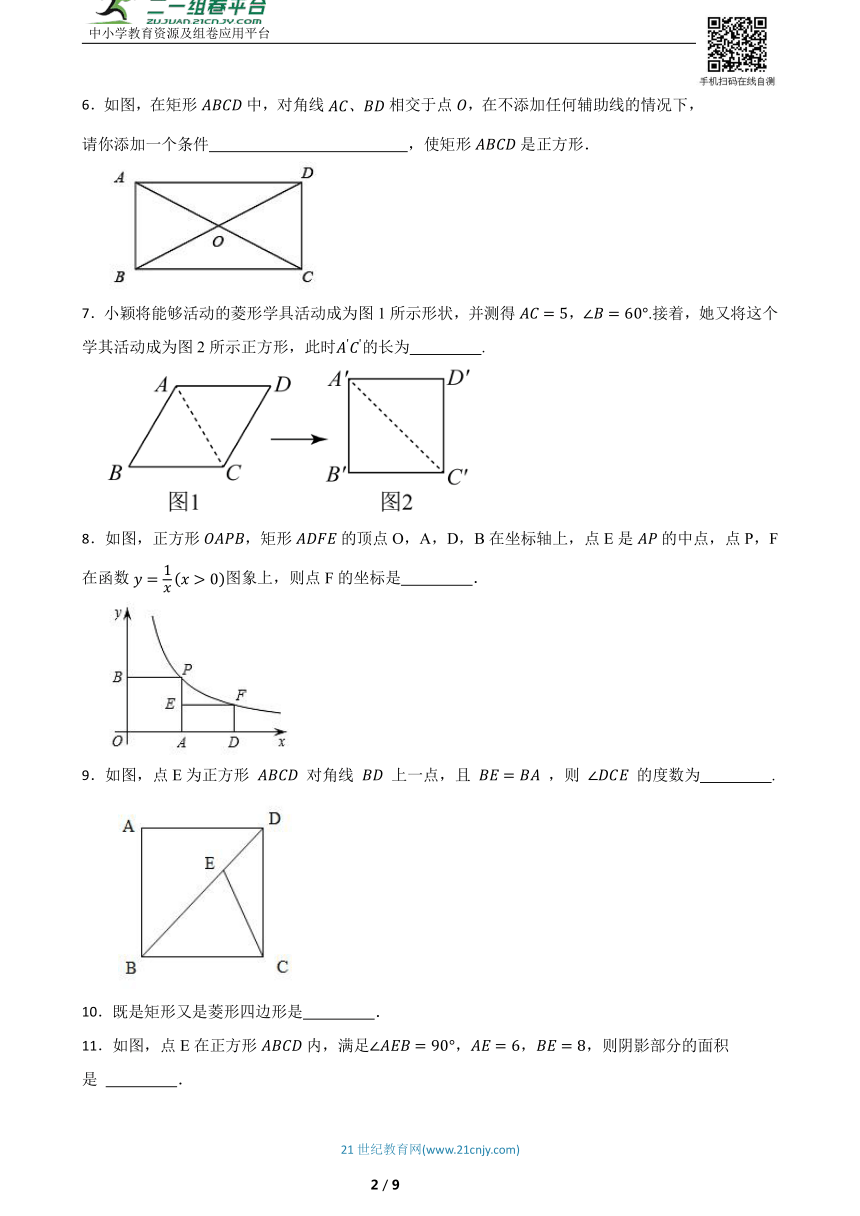
6.如图,在矩形中,对角线相交于点,在不添加任何辅助线的情况下,请你添加一个条件 ,使矩形是正方形.
7.小颖将能够活动的菱形学具活动成为图1所示形状,并测得,.接着,她又将这个学其活动成为图2所示正方形,此时的长为 .
8.如图,正方形,矩形的顶点O,A,D,B在坐标轴上,点E是的中点,点P,F在函数图象上,则点F的坐标是 .
9.如图,点E为正方形 对角线 上一点,且 ,则 的度数为 .
10.既是矩形又是菱形四边形是 .
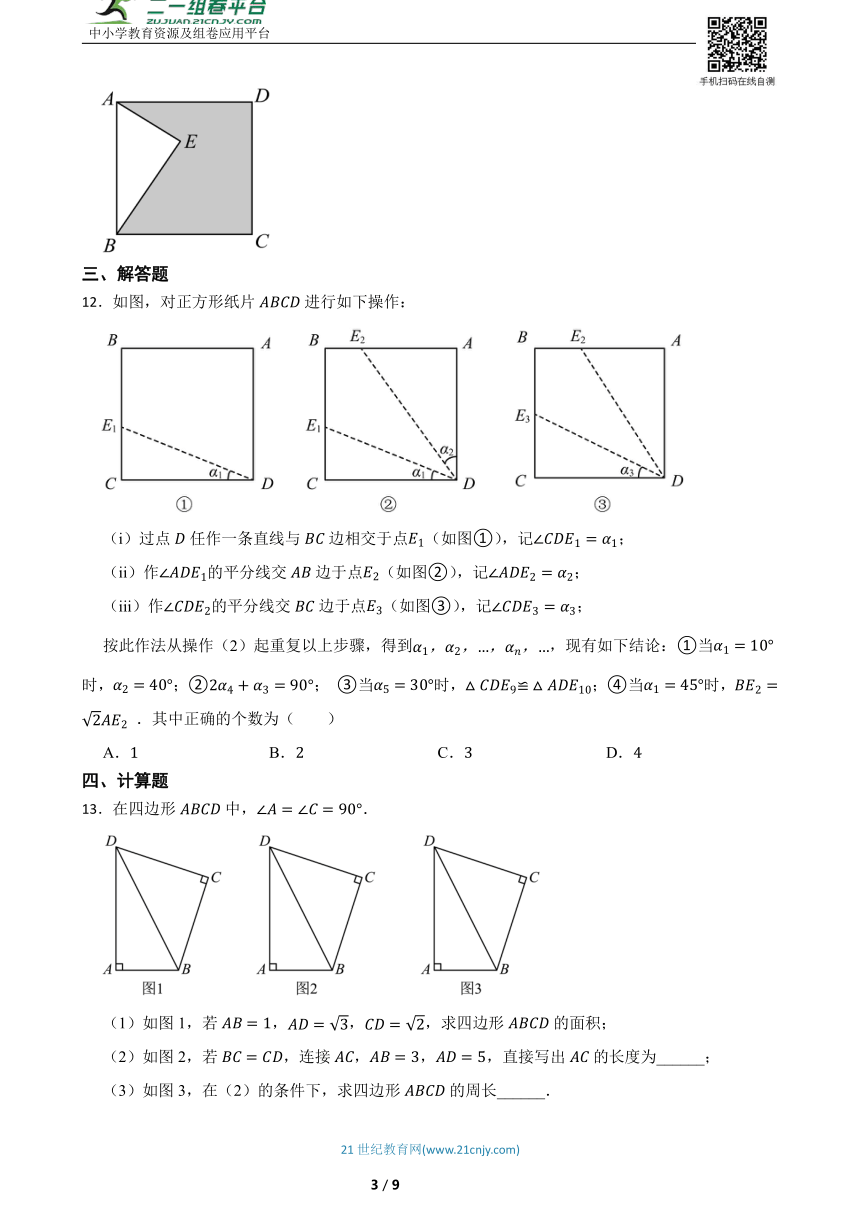
11.如图,点E在正方形内,满足,,,则阴影部分的面积是 .
三、解答题
12.如图,对正方形纸片进行如下操作:
(i)过点任作一条直线与边相交于点(如图①),记;
(ii)作的平分线交边于点(如图②),记;
(iii)作的平分线交边于点(如图③),记;
按此作法从操作(2)起重复以上步骤,得到,现有如下结论:①当时,;②; ③当时,;④当时, .其中正确的个数为( )
A. B. C. D.
四、计算题
13.在四边形中,.
(1)如图1,若,,,求四边形的面积;
(2)如图2,若,连接,,,直接写出的长度为______;
(3)如图3,在(2)的条件下,求四边形的周长______.
14.在菱形中,,点E、F分别为上一点.
(1)如图1,当,时,直接写出三条线段和之间满足的等量关系式为________;
(2)当时,
①如图2,若,若,,求的长;
②如图3,E为中点,交于点G,交于点H,和交于点O,若,,,则________.
五、作图题
15.如图,已知正方形,请用尺规作图法,在边上求作一点P,使.(保留作图痕迹,不写作法)
六、综合题
16.《九章算术》勾股章[一五]问“勾股容方”描述了关于图形之间关系的问题:如图,知道一个直角三角形较短直角边(“勾”)与较长直角边(“股”)的长度,那么,以该三角形的直角顶点为一个顶点、另外三个顶点分别在该三角形三边上的正方形的边长就可以求得.(我们不妨称这个正方形为该直角三角形的“所容正方形”)
其文如下:
问题:一个直角三角形两直角边的长分别为和,它的“所容正方形”的边长是多少?
答案:.
解:
(1)已知:如图,在中,,若,,求“所容正方形”的边长.
(2)应用(1)中的结论解决问题:如图,中山公园有一块菱形场地,其面积为,两条对角线长度之和为.现要在这个菱形场地上修建一个正方形花圃,并且要使正方形花圃的四个顶点分别落在菱形场地的四条边上,则该正方形花圃的边长为多少?
17.如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由
18.如图,四边形ABCD是正方形,△EBC是等边三角形.
(1)求证:△ABE≌△DCE;
(2)求∠AED的度数.
七、实践探究题
19.如图1,当时,与的面积相等.理由:因为,所以.又因为,所以.
(1)【类比探究】如图2,在正方形的右侧作等腰三角形,,连接,求的面积.
(2)【综合应用】如图3,在正方形的右侧作正方形,点B、C、E在同一直线上,,连接,求的面积.
答案解析部分
1.【答案】B
【知识点】正方形的判定
2.【答案】C
【知识点】三角形内角和定理;等腰三角形的性质;等边三角形的性质;正方形的性质
3.【答案】B
【知识点】菱形的性质;矩形的性质;正方形的性质
4.【答案】D
【知识点】菱形的判定;矩形的判定;正方形的判定
5.【答案】A
【知识点】三角形的面积;勾股定理;勾股定理的逆定理;正方形的性质
6.【答案】AC⊥BD(答案不唯一)
【知识点】正方形的判定
7.【答案】
【知识点】等边三角形的判定与性质;勾股定理;菱形的性质;正方形的性质
8.【答案】
【知识点】正方形的性质
9.【答案】22.5°
【知识点】三角形内角和定理;等腰三角形的性质;正方形的性质
10.【答案】正方形
【知识点】正方形的判定
11.【答案】76
【知识点】勾股定理;正方形的性质
12.【答案】D
【知识点】三角形全等及其性质;角平分线的性质;等腰三角形的判定与性质;正方形的性质
13.【答案】(1),
(2)
(3)
【知识点】勾股定理;正方形的判定与性质
14.【答案】(1)
(2);
【知识点】等边三角形的判定与性质;勾股定理;正方形的性质
15.【答案】解:如图,点即为所求.
【知识点】含30°角的直角三角形;正方形的性质
16.【答案】(1)正方形边长为;
(2)该正方形花圃的边长为.
【知识点】菱形的性质;正方形的判定与性质
17.【答案】(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴平行四边形AEBD是矩形
(2)解:当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,
∴AD=BD=CD,
∵由(1)得四边形AEBD是矩形,
∴矩形AEBD是正方形
【知识点】正方形的判定
18.【答案】(1)证明:∵四边形ABCD是正方形,△ABC是等边三角形,
∴BA=BC=CD=BE=CE,∠ABC=∠BCD=90°,∠EBC=∠ECB=60°,
∴∠ABE=∠ECD=30°,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS)
(2)∵BA=BE,∠ABE=30°,
∴∠BAE= (180°﹣30°)=75°,
∵∠BAD=90°,
∴∠EAD=90°﹣75°=15°,同理可得∠ADE=15°,
∴∠AED=180°﹣15°﹣15°=150°.
【知识点】全等三角形的判定与性质;等边三角形的性质;正方形的性质
19.【答案】(1)4
(2)8
【知识点】正方形的性质
21世纪教育网(www.21cnjy.com)
1 / 9
18.2.3正方形
一、单选题
1.如图,在菱形中,对角线交于点,添加下列一个条件,能使菱形成为正方形的是( )
A. B. C. D.
2.如图,正方形ABCD外侧作等边三角形ADE,则∠AEB的度数为( )
A.30° B.20° C.15° D.10°
3.正方形 菱形 矩形都具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.对角线平分一组对角
4.下列说法中正确的是( )
A.两条对角线垂直的四边形是菱形
B.对角线垂直且相等的四边形是正方形
C.两条对角线相等的四边形是矩形
D.两条对角线相等的平行四边形是矩形
5.如图,在正方形 中, 是 的中点,点 在 上,且 .则 的面积是( )
A.5 B.6 C.7 D.8
二、填空题
6.如图,在矩形中,对角线相交于点,在不添加任何辅助线的情况下,请你添加一个条件 ,使矩形是正方形.
7.小颖将能够活动的菱形学具活动成为图1所示形状,并测得,.接着,她又将这个学其活动成为图2所示正方形,此时的长为 .
8.如图,正方形,矩形的顶点O,A,D,B在坐标轴上,点E是的中点,点P,F在函数图象上,则点F的坐标是 .
9.如图,点E为正方形 对角线 上一点,且 ,则 的度数为 .
10.既是矩形又是菱形四边形是 .
11.如图,点E在正方形内,满足,,,则阴影部分的面积是 .
三、解答题
12.如图,对正方形纸片进行如下操作:
(i)过点任作一条直线与边相交于点(如图①),记;
(ii)作的平分线交边于点(如图②),记;
(iii)作的平分线交边于点(如图③),记;
按此作法从操作(2)起重复以上步骤,得到,现有如下结论:①当时,;②; ③当时,;④当时, .其中正确的个数为( )
A. B. C. D.
四、计算题
13.在四边形中,.
(1)如图1,若,,,求四边形的面积;
(2)如图2,若,连接,,,直接写出的长度为______;
(3)如图3,在(2)的条件下,求四边形的周长______.
14.在菱形中,,点E、F分别为上一点.
(1)如图1,当,时,直接写出三条线段和之间满足的等量关系式为________;
(2)当时,
①如图2,若,若,,求的长;
②如图3,E为中点,交于点G,交于点H,和交于点O,若,,,则________.
五、作图题
15.如图,已知正方形,请用尺规作图法,在边上求作一点P,使.(保留作图痕迹,不写作法)
六、综合题
16.《九章算术》勾股章[一五]问“勾股容方”描述了关于图形之间关系的问题:如图,知道一个直角三角形较短直角边(“勾”)与较长直角边(“股”)的长度,那么,以该三角形的直角顶点为一个顶点、另外三个顶点分别在该三角形三边上的正方形的边长就可以求得.(我们不妨称这个正方形为该直角三角形的“所容正方形”)
其文如下:
问题:一个直角三角形两直角边的长分别为和,它的“所容正方形”的边长是多少?
答案:.
解:
(1)已知:如图,在中,,若,,求“所容正方形”的边长.
(2)应用(1)中的结论解决问题:如图,中山公园有一块菱形场地,其面积为,两条对角线长度之和为.现要在这个菱形场地上修建一个正方形花圃,并且要使正方形花圃的四个顶点分别落在菱形场地的四条边上,则该正方形花圃的边长为多少?
17.如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由
18.如图,四边形ABCD是正方形,△EBC是等边三角形.
(1)求证:△ABE≌△DCE;
(2)求∠AED的度数.
七、实践探究题
19.如图1,当时,与的面积相等.理由:因为,所以.又因为,所以.
(1)【类比探究】如图2,在正方形的右侧作等腰三角形,,连接,求的面积.
(2)【综合应用】如图3,在正方形的右侧作正方形,点B、C、E在同一直线上,,连接,求的面积.
答案解析部分
1.【答案】B
【知识点】正方形的判定
2.【答案】C
【知识点】三角形内角和定理;等腰三角形的性质;等边三角形的性质;正方形的性质
3.【答案】B
【知识点】菱形的性质;矩形的性质;正方形的性质
4.【答案】D
【知识点】菱形的判定;矩形的判定;正方形的判定
5.【答案】A
【知识点】三角形的面积;勾股定理;勾股定理的逆定理;正方形的性质
6.【答案】AC⊥BD(答案不唯一)
【知识点】正方形的判定
7.【答案】
【知识点】等边三角形的判定与性质;勾股定理;菱形的性质;正方形的性质
8.【答案】
【知识点】正方形的性质
9.【答案】22.5°
【知识点】三角形内角和定理;等腰三角形的性质;正方形的性质
10.【答案】正方形
【知识点】正方形的判定
11.【答案】76
【知识点】勾股定理;正方形的性质
12.【答案】D
【知识点】三角形全等及其性质;角平分线的性质;等腰三角形的判定与性质;正方形的性质
13.【答案】(1),
(2)
(3)
【知识点】勾股定理;正方形的判定与性质
14.【答案】(1)
(2);
【知识点】等边三角形的判定与性质;勾股定理;正方形的性质
15.【答案】解:如图,点即为所求.
【知识点】含30°角的直角三角形;正方形的性质
16.【答案】(1)正方形边长为;
(2)该正方形花圃的边长为.
【知识点】菱形的性质;正方形的判定与性质
17.【答案】(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴平行四边形AEBD是矩形
(2)解:当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,
∴AD=BD=CD,
∵由(1)得四边形AEBD是矩形,
∴矩形AEBD是正方形
【知识点】正方形的判定
18.【答案】(1)证明:∵四边形ABCD是正方形,△ABC是等边三角形,
∴BA=BC=CD=BE=CE,∠ABC=∠BCD=90°,∠EBC=∠ECB=60°,
∴∠ABE=∠ECD=30°,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS)
(2)∵BA=BE,∠ABE=30°,
∴∠BAE= (180°﹣30°)=75°,
∵∠BAD=90°,
∴∠EAD=90°﹣75°=15°,同理可得∠ADE=15°,
∴∠AED=180°﹣15°﹣15°=150°.
【知识点】全等三角形的判定与性质;等边三角形的性质;正方形的性质
19.【答案】(1)4
(2)8
【知识点】正方形的性质
21世纪教育网(www.21cnjy.com)
1 / 9
