第18章 平行四边形(培优)(含答案)
文档属性
| 名称 | 第18章 平行四边形(培优)(含答案) | 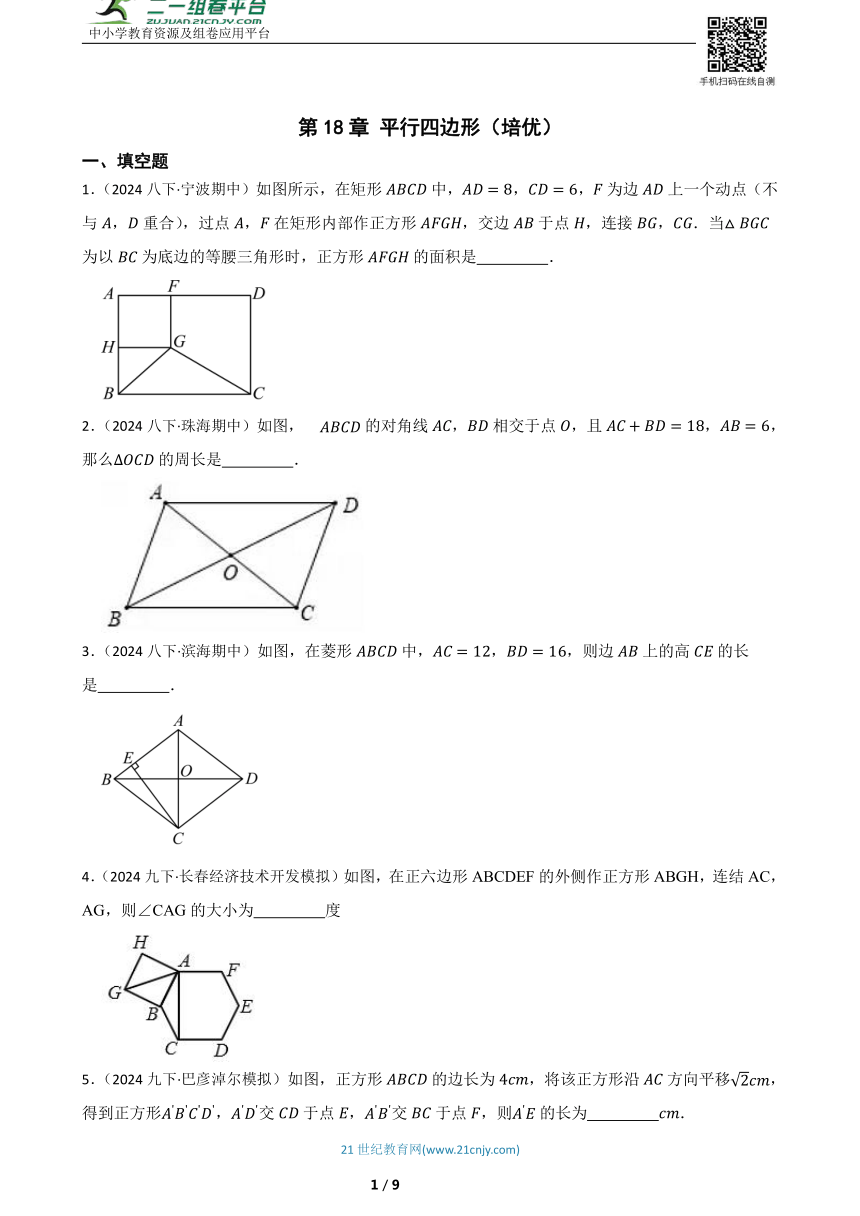 | |
| 格式 | docx | ||
| 文件大小 | 828.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-21 16:31:23 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第18章 平行四边形(培优)
一、填空题
1.(2024八下·宁波期中)如图所示,在矩形中,,,为边上一个动点(不与,重合),过点,在矩形内部作正方形,交边于点,连接,.当为以为底边的等腰三角形时,正方形的面积是 .
2.(2024八下·珠海期中)如图,的对角线,相交于点,且,,那么的周长是 .
3.(2024八下·滨海期中)如图,在菱形中,,,则边上的高的长是 .
4.(2024九下·长春经济技术开发模拟)如图,在正六边形ABCDEF的外侧作正方形ABGH,连结AC,AG,则∠CAG的大小为 度
5.(2024九下·巴彦淖尔模拟)如图,正方形的边长为,将该正方形沿方向平移,得到正方形,交于点,交于点,则的长为 .
6.(2024八下·大武口月考)如图,是利用四边形的不稳定性制作的菱形晾衣架,已知每个菱形的边长为20cm,,则在墙上悬挂晾衣架的两个铁钉A,B间的距离是 cm.
二、单选题
7.(2024九上·武侯月考)如图,四边形是平行四边形,下列结论中错误的是( )
A.当,平行四边形是矩形
B.当,平行四边形是矩形
C.当,平行四边形是菱形
D.当,平行四边形是正方形
8.下列说法错误的是( )
A.邻边相等的矩形是正方形
B.对角线相等的平行四边形是矩形
C.顺次连结菱形各边中点, 所得的四边形是菱形
D.对角线互相垂直的矩形是正方形
9.(2024九下·东营模拟)如图,两直线,将一块直角三角板的角的顶点A与直角顶点C分别在两直线上,斜边交直线于点D,当点D为的中点时,则的度数为( )
A. B. C. D.
10.(2024九下·苏州工业园月考)如图,反比例函数(x>0)的图象经过□OABC的顶点C和对角线的交点E,顶点A在x轴上,若□OABC的面积为18,则k的值为( )
A.8 B.6 C.4 D.2
11.(2023九上·南海月考)如图,菱形中,对角线、相交于点O,H为边中点,菱形的周长为28,则的长等于( )
A. B.4 C.7 D.14
12.(2024九下·东昌府模拟)如图,在正方形中,.则下列结论:①;②;③连接,若的面积为,则的长为5.其中正确的结论是( )
A.①② B.①②③ C.①③ D.②③
13.(2024八下·北京市期中)如图,菱形ABCD的周长为24,∠ABD=30°,Q是BC的中点,则PC+ PQ的最小值是( )
A.6 B.3 C.3 D.6
14.(2024八下·龙门期中)如图,已知菱形,,,为的中点,为对角线上一点,则的最小值等于( )
A. B. C. D.8
15.(2024八上·邯郸月考)如图,正方形的边长为,则图中阴影部分面积为( )
A. B. C. D.
16.(2024九上·上城月考)以下说法正确的是( )
A.某彩票的中奖概率是,那么买100张彩票一定有5张中奖
B.经过有交通信号灯的路口,遇到绿灯概率为
C.“任意画出一个平行四边形,它是中心对称图形”是必然事件
D.张东做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率是
三、解答题
17.(2023九上·孝昌开学考)如图,四边形 ABCD 为平行四边形, ∠BAD 的平分线 AE 交 CD 于点 F ,交 BC 的延长线于点 E .
(1)求证: BE = CD ;
(2)连接BF,若BF⊥AE , ∠BEA =60°, AB =2,求平行四边形 ABCD 的面积.
18.(2023九上·榕城期中)在菱形中,点E是边的中点,试分别在下列两个图形中按要求仅使用无刻度的直尺作图.
(1)在图1中,过点E作线段,交于点F,并说明的理由;
(2)在图2中,连接,在上找一点,使的值最小(不需说明理由).
19.(2024八下·宝安月考)如图,点是正方形的边上一点,把顺时针旋转至的位置.
(1)旋转中心是 ________点,旋转角度是 _______度,则是 _______三角形;
(2)若四边形的面积为,求EF的长.
20.(2024八下·绥中期中)如图,在四边形中,.
(1)求的长;
(2)求四边形的面积.
四、计算题
21.(2023八上·江都月考)已知,如图所示,折叠长方形的一边,使点落在边的点处,已知,求:
(1)求的坐标;
(2)求的坐标.
22.(2023九下·袁州模拟)(1)计算:;
(2)如图,在菱形中,,E是上一点,M、N分别是、的中点,且,求菱形的周长;
23.(2024九下·高安模拟)(1)计算:;
(2)如图,矩形中,,,以点D为圆心,为半径画弧,交边于点E,连接,求的长.
答案解析部分
1.【答案】
【知识点】等腰三角形的判定与性质;矩形的性质;正方形的性质
2.【答案】15
【知识点】平行四边形的性质
3.【答案】
【知识点】勾股定理;菱形的性质
4.【答案】75
【知识点】三角形内角和定理;等腰三角形的判定与性质;多边形内角与外角;正方形的性质
5.【答案】
【知识点】勾股定理;正方形的性质;平移的性质
6.【答案】
【知识点】等边三角形的判定与性质;含30°角的直角三角形;勾股定理;菱形的性质
7.【答案】D
【知识点】菱形的判定;矩形的判定;正方形的判定
8.【答案】C
【知识点】矩形的判定;正方形的判定
9.【答案】D
【知识点】平行线的性质;直角三角形斜边上的中线
10.【答案】B
【知识点】反比例函数系数k的几何意义;平行四边形的性质
11.【答案】A
【知识点】菱形的性质;直角三角形斜边上的中线
12.【答案】A
【知识点】勾股定理;正方形的性质;相似三角形的判定与性质
13.【答案】B
【知识点】等边三角形的判定与性质;勾股定理;菱形的性质;轴对称的性质
14.【答案】B
【知识点】两点之间线段最短;等边三角形的判定与性质;勾股定理;菱形的性质;轴对称的应用-最短距离问题
15.【答案】B
【知识点】正方形的性质
16.【答案】C
【知识点】平行四边形的性质;事件的分类;概率的意义
17.【答案】(1)解: 证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠E,
又∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠E=∠BAE,
∴BA=BE,
∴BE=CD;
(2)解:∵AB=BE,∠BEA=60°,
∴△ABE是等边三角形,
∴AE=AB=2,
∵BF⊥AE,
∴AF=EF=1,
∴BF= ,
∵AD∥BC,
∴∠D=∠ECF,∠DAF=∠E,
在△ADF和△ECF中,
∴△ADF≌△ECF(AAS),
∴△ADF的面积=△ECF的面积,
∴平行四边形ABCD的面积=△ABE的面积=AE BF=.
故答案为:.
【知识点】角平分线的性质;等腰三角形的判定与性质;勾股定理的应用;平行四边形的性质
18.【答案】(1)解:如图,连接、交于点O,连接并延长交于点F,则线段为所求.
理由如下:四边形为菱形,
点O为的中点
点E为的中点,
为的中位线,
,即;
(2):如图,连接交于点,则点即为所求.
【知识点】菱形的性质;三角形的中位线定理
19.【答案】(1),,等腰直角
(2)
【知识点】三角形全等及其性质;勾股定理;正方形的性质;旋转的性质
20.【答案】(1)
(2)
【知识点】勾股定理;平行四边形的判定与性质
21.【答案】(1)
(2)
【知识点】勾股定理;矩形的性质
22.【答案】(1);(2)16
【知识点】分式的加减法;菱形的性质;三角形的中位线定理
23.【答案】(1);(2)
【知识点】负整数指数幂;勾股定理;矩形的性质;求特殊角的三角函数值
21世纪教育网(www.21cnjy.com)
2 / 9
第18章 平行四边形(培优)
一、填空题
1.(2024八下·宁波期中)如图所示,在矩形中,,,为边上一个动点(不与,重合),过点,在矩形内部作正方形,交边于点,连接,.当为以为底边的等腰三角形时,正方形的面积是 .
2.(2024八下·珠海期中)如图,的对角线,相交于点,且,,那么的周长是 .
3.(2024八下·滨海期中)如图,在菱形中,,,则边上的高的长是 .
4.(2024九下·长春经济技术开发模拟)如图,在正六边形ABCDEF的外侧作正方形ABGH,连结AC,AG,则∠CAG的大小为 度
5.(2024九下·巴彦淖尔模拟)如图,正方形的边长为,将该正方形沿方向平移,得到正方形,交于点,交于点,则的长为 .
6.(2024八下·大武口月考)如图,是利用四边形的不稳定性制作的菱形晾衣架,已知每个菱形的边长为20cm,,则在墙上悬挂晾衣架的两个铁钉A,B间的距离是 cm.
二、单选题
7.(2024九上·武侯月考)如图,四边形是平行四边形,下列结论中错误的是( )
A.当,平行四边形是矩形
B.当,平行四边形是矩形
C.当,平行四边形是菱形
D.当,平行四边形是正方形
8.下列说法错误的是( )
A.邻边相等的矩形是正方形
B.对角线相等的平行四边形是矩形
C.顺次连结菱形各边中点, 所得的四边形是菱形
D.对角线互相垂直的矩形是正方形
9.(2024九下·东营模拟)如图,两直线,将一块直角三角板的角的顶点A与直角顶点C分别在两直线上,斜边交直线于点D,当点D为的中点时,则的度数为( )
A. B. C. D.
10.(2024九下·苏州工业园月考)如图,反比例函数(x>0)的图象经过□OABC的顶点C和对角线的交点E,顶点A在x轴上,若□OABC的面积为18,则k的值为( )
A.8 B.6 C.4 D.2
11.(2023九上·南海月考)如图,菱形中,对角线、相交于点O,H为边中点,菱形的周长为28,则的长等于( )
A. B.4 C.7 D.14
12.(2024九下·东昌府模拟)如图,在正方形中,.则下列结论:①;②;③连接,若的面积为,则的长为5.其中正确的结论是( )
A.①② B.①②③ C.①③ D.②③
13.(2024八下·北京市期中)如图,菱形ABCD的周长为24,∠ABD=30°,Q是BC的中点,则PC+ PQ的最小值是( )
A.6 B.3 C.3 D.6
14.(2024八下·龙门期中)如图,已知菱形,,,为的中点,为对角线上一点,则的最小值等于( )
A. B. C. D.8
15.(2024八上·邯郸月考)如图,正方形的边长为,则图中阴影部分面积为( )
A. B. C. D.
16.(2024九上·上城月考)以下说法正确的是( )
A.某彩票的中奖概率是,那么买100张彩票一定有5张中奖
B.经过有交通信号灯的路口,遇到绿灯概率为
C.“任意画出一个平行四边形,它是中心对称图形”是必然事件
D.张东做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率是
三、解答题
17.(2023九上·孝昌开学考)如图,四边形 ABCD 为平行四边形, ∠BAD 的平分线 AE 交 CD 于点 F ,交 BC 的延长线于点 E .
(1)求证: BE = CD ;
(2)连接BF,若BF⊥AE , ∠BEA =60°, AB =2,求平行四边形 ABCD 的面积.
18.(2023九上·榕城期中)在菱形中,点E是边的中点,试分别在下列两个图形中按要求仅使用无刻度的直尺作图.
(1)在图1中,过点E作线段,交于点F,并说明的理由;
(2)在图2中,连接,在上找一点,使的值最小(不需说明理由).
19.(2024八下·宝安月考)如图,点是正方形的边上一点,把顺时针旋转至的位置.
(1)旋转中心是 ________点,旋转角度是 _______度,则是 _______三角形;
(2)若四边形的面积为,求EF的长.
20.(2024八下·绥中期中)如图,在四边形中,.
(1)求的长;
(2)求四边形的面积.
四、计算题
21.(2023八上·江都月考)已知,如图所示,折叠长方形的一边,使点落在边的点处,已知,求:
(1)求的坐标;
(2)求的坐标.
22.(2023九下·袁州模拟)(1)计算:;
(2)如图,在菱形中,,E是上一点,M、N分别是、的中点,且,求菱形的周长;
23.(2024九下·高安模拟)(1)计算:;
(2)如图,矩形中,,,以点D为圆心,为半径画弧,交边于点E,连接,求的长.
答案解析部分
1.【答案】
【知识点】等腰三角形的判定与性质;矩形的性质;正方形的性质
2.【答案】15
【知识点】平行四边形的性质
3.【答案】
【知识点】勾股定理;菱形的性质
4.【答案】75
【知识点】三角形内角和定理;等腰三角形的判定与性质;多边形内角与外角;正方形的性质
5.【答案】
【知识点】勾股定理;正方形的性质;平移的性质
6.【答案】
【知识点】等边三角形的判定与性质;含30°角的直角三角形;勾股定理;菱形的性质
7.【答案】D
【知识点】菱形的判定;矩形的判定;正方形的判定
8.【答案】C
【知识点】矩形的判定;正方形的判定
9.【答案】D
【知识点】平行线的性质;直角三角形斜边上的中线
10.【答案】B
【知识点】反比例函数系数k的几何意义;平行四边形的性质
11.【答案】A
【知识点】菱形的性质;直角三角形斜边上的中线
12.【答案】A
【知识点】勾股定理;正方形的性质;相似三角形的判定与性质
13.【答案】B
【知识点】等边三角形的判定与性质;勾股定理;菱形的性质;轴对称的性质
14.【答案】B
【知识点】两点之间线段最短;等边三角形的判定与性质;勾股定理;菱形的性质;轴对称的应用-最短距离问题
15.【答案】B
【知识点】正方形的性质
16.【答案】C
【知识点】平行四边形的性质;事件的分类;概率的意义
17.【答案】(1)解: 证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠E,
又∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠E=∠BAE,
∴BA=BE,
∴BE=CD;
(2)解:∵AB=BE,∠BEA=60°,
∴△ABE是等边三角形,
∴AE=AB=2,
∵BF⊥AE,
∴AF=EF=1,
∴BF= ,
∵AD∥BC,
∴∠D=∠ECF,∠DAF=∠E,
在△ADF和△ECF中,
∴△ADF≌△ECF(AAS),
∴△ADF的面积=△ECF的面积,
∴平行四边形ABCD的面积=△ABE的面积=AE BF=.
故答案为:.
【知识点】角平分线的性质;等腰三角形的判定与性质;勾股定理的应用;平行四边形的性质
18.【答案】(1)解:如图,连接、交于点O,连接并延长交于点F,则线段为所求.
理由如下:四边形为菱形,
点O为的中点
点E为的中点,
为的中位线,
,即;
(2):如图,连接交于点,则点即为所求.
【知识点】菱形的性质;三角形的中位线定理
19.【答案】(1),,等腰直角
(2)
【知识点】三角形全等及其性质;勾股定理;正方形的性质;旋转的性质
20.【答案】(1)
(2)
【知识点】勾股定理;平行四边形的判定与性质
21.【答案】(1)
(2)
【知识点】勾股定理;矩形的性质
22.【答案】(1);(2)16
【知识点】分式的加减法;菱形的性质;三角形的中位线定理
23.【答案】(1);(2)
【知识点】负整数指数幂;勾股定理;矩形的性质;求特殊角的三角函数值
21世纪教育网(www.21cnjy.com)
2 / 9
