19.1.2函数的图像(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
19.1.2函数的图像
一、单选题
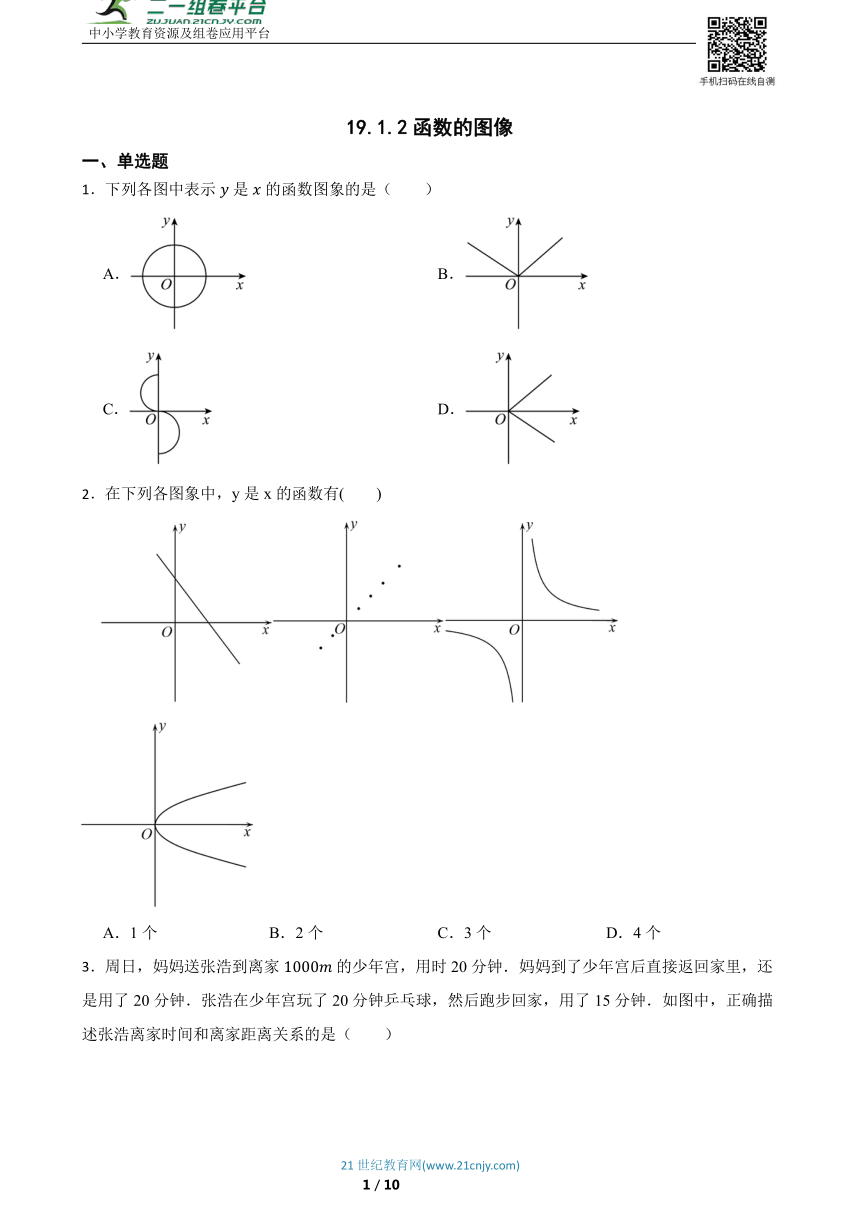
1.下列各图中表示是的函数图象的是( )
A. B.
C. D.
2.在下列各图象中,y是x的函数有( )
A.1个 B.2个 C.3个 D.4个
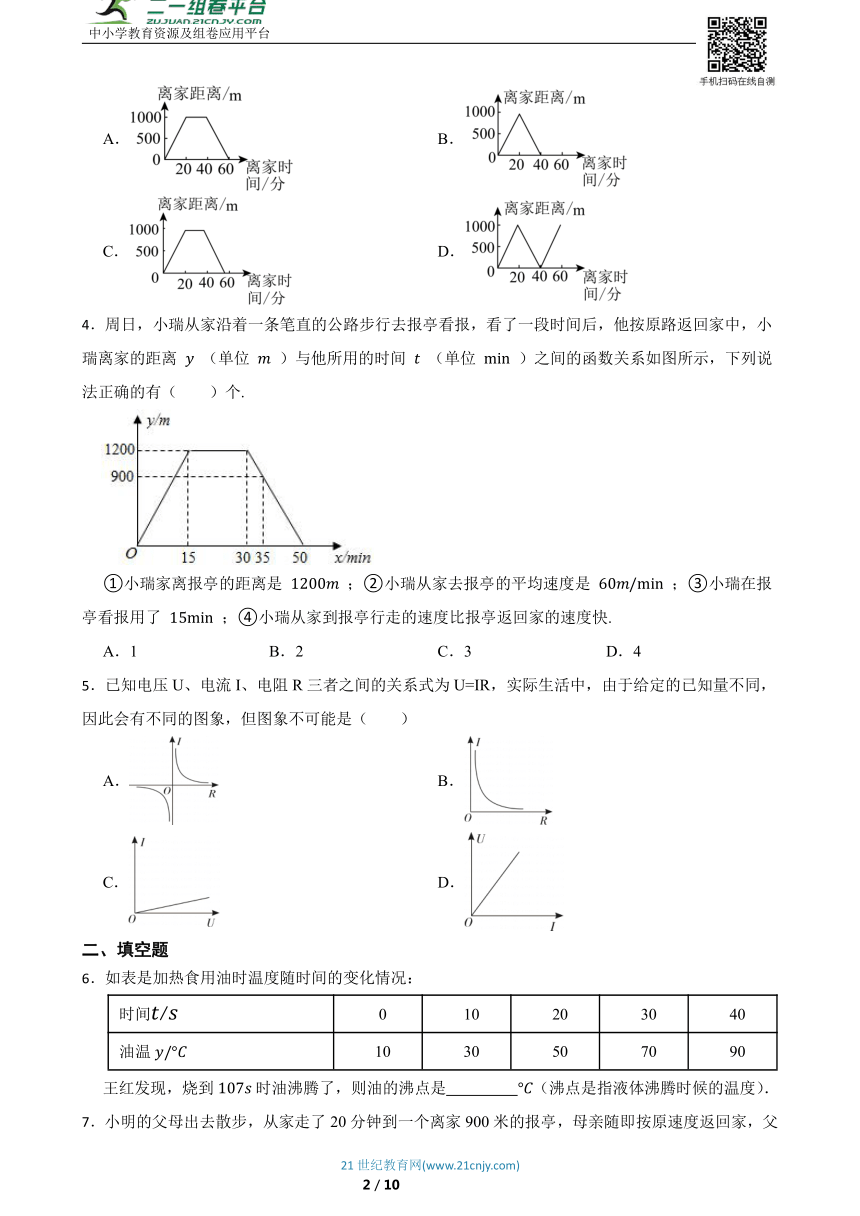
3.周日,妈妈送张浩到离家的少年宫,用时20分钟.妈妈到了少年宫后直接返回家里,还是用了20分钟.张浩在少年宫玩了20分钟乒乓球,然后跑步回家,用了15分钟.如图中,正确描述张浩离家时间和离家距离关系的是( )
A. B.
C. D.
4.周日,小瑞从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小瑞离家的距离 (单位 )与他所用的时间 (单位 )之间的函数关系如图所示,下列说法正确的有( )个.
①小瑞家离报亭的距离是 ;②小瑞从家去报亭的平均速度是 ;③小瑞在报亭看报用了 ;④小瑞从家到报亭行走的速度比报亭返回家的速度快.
A.1 B.2 C.3 D.4
5.已知电压U、电流I、电阻R三者之间的关系式为U=IR,实际生活中,由于给定的已知量不同,因此会有不同的图象,但图象不可能是( )
A. B.
C. D.
二、填空题
6.如表是加热食用油时温度随时间的变化情况:
时间 0 10 20 30 40
油温 10 30 50 70 90
王红发现,烧到时油沸腾了,则油的沸点是 (沸点是指液体沸腾时候的温度).
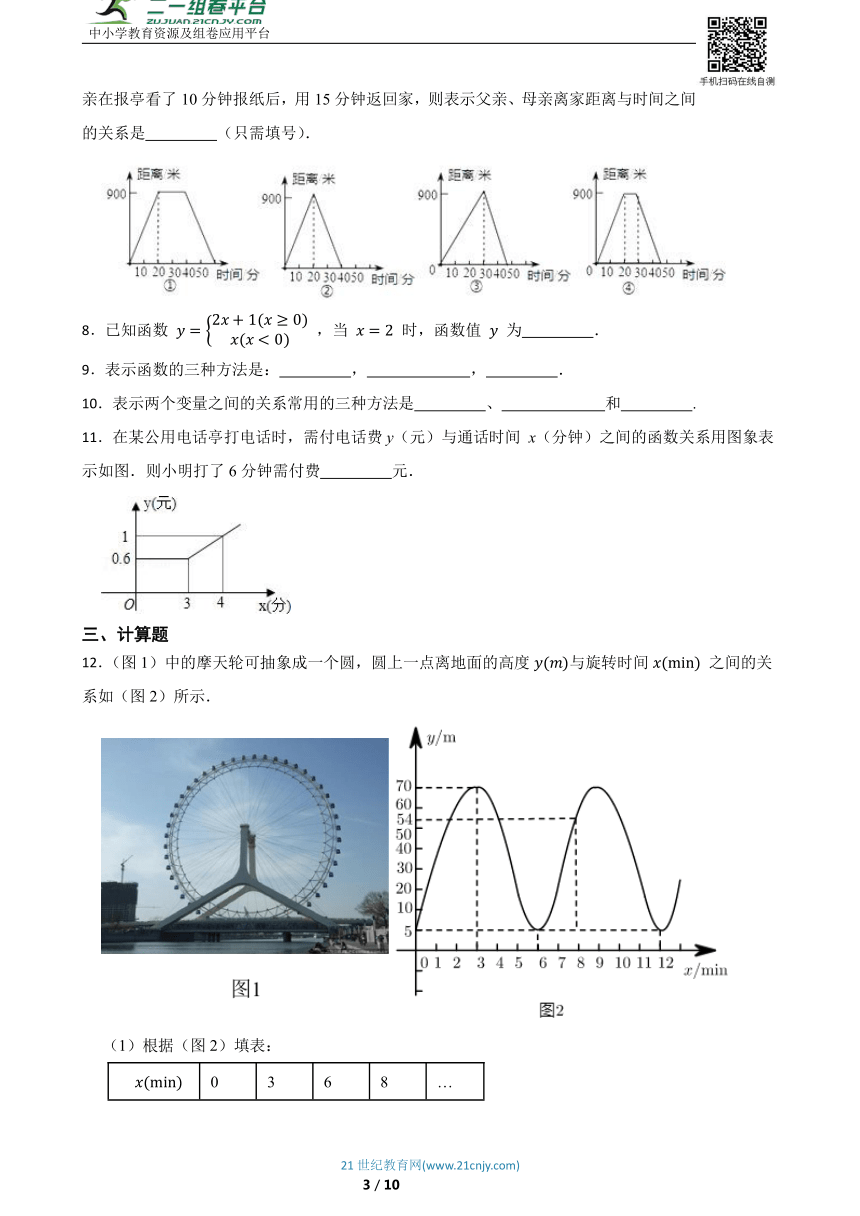
7.小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则表示父亲、母亲离家距离与时间之间的关系是 (只需填号).
8.已知函数 ,当 时,函数值 为 .
9.表示函数的三种方法是: , , .
10.表示两个变量之间的关系常用的三种方法是 、 和 .
11.在某公用电话亭打电话时,需付电话费y(元)与通话时间 x(分钟)之间的函数关系用图象表示如图.则小明打了6分钟需付费 元.
三、计算题
12.(图1)中的摩天轮可抽象成一个圆,圆上一点离地面的高度与旋转时间 之间的关系如(图2)所示.
(1)根据(图2)填表:
0 3 6 8 …
…
(2)根据图中的信息,请写出摩天轮的直径.
13.在平面直角坐标系中,对于任意三点的“矩面积”,给出如下定义:“水平底”是任意两点横坐标差的最大值;“铅垂高”是任意两点纵坐标差的最大值,则“矩面积”.例如:三点的坐标分别为,则“水平底”,“铅垂高”,“矩面积”.根据所给定义解决下面的问题:
(1)若点的坐标分别为,求这三点的“矩面积”;
(2)若点,含有的式子表示这三点的“矩面积”(结果需化简);
(3)已知点,在轴上是否存在点,使这三点的“矩面积”为20?若存在,求出点的坐标;若不存在,请说明理由.
四、解答题
14.小明家、食堂、图书馆在同一条直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.小明离家的距离与时间之间的对应关系如图所示.
根据上图回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
(2)小明吃早餐用了多少时间?在图书馆停留了多少时间?
(3)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
五、作图题
15.已知二次函数
(1)完成下表;
(2)在如图的坐标系中描点,画出该二次函数的图象.
六、综合题
16.心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间有如下关系:(其中0≤x≤30)
提出概念所用时间(x) 2 5 7 10 12 13 14 17 20
对概念的接受能力(y) 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55
(1)上表中反映了哪两个变量之间的关系?
(2)当提出概念所用时间是10分钟时,学生的接受能力是多少?
(3)根据表格中的数据,你认为提出概念几分钟时,学生的接受能力最强;
(4)从表中可知,当时间x在什么范围内,学生的接受能力逐步增强?当时间x在什么范围内,学生的接受能力逐步降低?
17.由于惯性的作用,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号小型载客汽车的刹车性能(车速不超过),对这种型号的汽车进行了测试,测得的数据如下表:
刹车时车速 0 10 20 30 40 50 …
刹车距离 0 5 10 …
谛回答下列问题:
(1)当刹车时车速为时,刹车距离是_______m;
(2)根据上表反映的规律写出该种型号汽车s与v之间的关系式:_________;
(3)该型号汽车在高速公路上发生了一次交通事故,现场测得刹车距离为,推测刹车时车速是多少?并说明事故发生时,汽车是超速行驶还是正常行驶? (相关法规:《道路交通安全法》第七十八条:高速公路上行驶的小型载客汽车最高车速不得超过每小时120公里.)
18.人的大脑所能记忆的内容是有限的,随着时间的推移,记忆的内容逐渐被遗忘.德国心理学家艾宾浩威斯第一个发现了记忆遗忘规律,他根据自己研究得到的测试数据描绘了一条曲线(如图所示),这就是著名的艾宾浩威斯遗忘曲线,其中纵轴表示学习中的记忆保持量,横轴表示时间.观察图象并回答下列问题:
(1)学习后2h的时候,记忆保持量约是多少
(2)图中A点表示的实际意义是什么 在哪个时间段内遗忘的速度最快
(3)有研究表明,如及时复习,一天后能保持98%.根据遗忘曲线,如不复习,会有什么样的结果 小明说学习中能记住不过一会就忘了,都是因为自己笨.你同意他这样的说法吗 你会给他提出什么建议
答案解析部分
1.【答案】B
【知识点】函数的概念;函数的图象
2.【答案】C
【知识点】函数的图象
3.【答案】C
【知识点】函数的图象
4.【答案】C
【知识点】函数的图象
5.【答案】A
【知识点】函数的图象
6.【答案】224
【知识点】函数的表示方法
7.【答案】④②
【知识点】函数的图象
8.【答案】5
【知识点】分段函数
9.【答案】列表法;解析式法;图象法
【知识点】函数的表示方法
10.【答案】表格法;关系式法;图象法
【知识点】函数的表示方法
11.【答案】1.8
【知识点】分段函数
12.【答案】(1)解:结合图象填表如下:
x(min) 0 3 6 8 …
y(m) 5 70 5 54 …
(2)解:∵最高点为70米,最低点为5米,
∴摩天轮的直径为65米.
【知识点】函数的图象
13.【答案】解:(1)∵点D(-1,2)、E(2,-1)、F(0,6),如图:
∴,,
∴,
(2)∵点D(2,3)、E(2,-1)、F(t,-2),
∵D,E两点的横坐标相同,
∴,,
∴,
当时,,
当时,,
综上可得:;
(3)设点F的坐标为(,0),
∵点D(-1,2)、E(2,-2)、F(,0),
∴,
当点F在点D左侧,即x<-1时,如图:
则,
∴,故.
解得:,
∴点F的坐标为(,0).
当点F在点D、E之间,即-1∴“矩面积”,
∴点F在点D、E之间时,不存在点F,使这三点的“矩面积”S为20.
当点F在点E右侧时,即x>2时,如图:
则,
∴,故.
解得:x=4,
∴点F的坐标为(,0).
综上,当点F的坐标为(,0)或(,0)时,这三点的“矩面积”为20.
【知识点】坐标与图形性质;分段函数
14.【答案】(1),
(2),
(3),
【知识点】函数的图象
15.【答案】(1)解:完成表格如下:
0 1 2 3 4
0
(2)解:描点,画出该二次函数图象如下:
【知识点】函数值;描点法画函数图象
16.【答案】(1)解:提出概念所用时间x和提出概念的接受能力y两个变量
(2)解:当x=10时,y=59,所以时间是10分钟,学生的接受能力是59
(3)解:当x=13时,y的值最大是59.9,所以提出概念13分钟时,学生的接受能力最强
(4)解:由表中数据可知:当2x<20时,y值逐渐减小,学生的接受能力逐步降低
【知识点】常量、变量;函数的表示方法
17.【答案】(1)
(2)
(3)推测刹车时车速是,所以事故发生时,汽车是超速行驶.
【知识点】函数解析式;函数自变量的取值范围;函数的表示方法
18.【答案】(1)解:由图可知,学习后2h的时候﹐记忆保持量约是40%;
(2)解:图中A点表示的实际意义是学习后15时的记忆保持量约为35%.在0-2h时间段内遗忘的速度最快
(3)解:如不复习﹐会很快忘掉很多﹐只能保持大约30%的记忆保持量;不同意小明的说法,记不住并不是因为笨﹐而是没有及时做好复习﹐建议在学习的一天内及时进行或多次复习(言之有理即可).
【知识点】函数的图象
21世纪教育网(www.21cnjy.com)
2 / 10
19.1.2函数的图像
一、单选题
1.下列各图中表示是的函数图象的是( )
A. B.
C. D.
2.在下列各图象中,y是x的函数有( )
A.1个 B.2个 C.3个 D.4个
3.周日,妈妈送张浩到离家的少年宫,用时20分钟.妈妈到了少年宫后直接返回家里,还是用了20分钟.张浩在少年宫玩了20分钟乒乓球,然后跑步回家,用了15分钟.如图中,正确描述张浩离家时间和离家距离关系的是( )
A. B.
C. D.
4.周日,小瑞从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小瑞离家的距离 (单位 )与他所用的时间 (单位 )之间的函数关系如图所示,下列说法正确的有( )个.
①小瑞家离报亭的距离是 ;②小瑞从家去报亭的平均速度是 ;③小瑞在报亭看报用了 ;④小瑞从家到报亭行走的速度比报亭返回家的速度快.
A.1 B.2 C.3 D.4
5.已知电压U、电流I、电阻R三者之间的关系式为U=IR,实际生活中,由于给定的已知量不同,因此会有不同的图象,但图象不可能是( )
A. B.
C. D.
二、填空题
6.如表是加热食用油时温度随时间的变化情况:
时间 0 10 20 30 40
油温 10 30 50 70 90
王红发现,烧到时油沸腾了,则油的沸点是 (沸点是指液体沸腾时候的温度).
7.小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则表示父亲、母亲离家距离与时间之间的关系是 (只需填号).
8.已知函数 ,当 时,函数值 为 .
9.表示函数的三种方法是: , , .
10.表示两个变量之间的关系常用的三种方法是 、 和 .
11.在某公用电话亭打电话时,需付电话费y(元)与通话时间 x(分钟)之间的函数关系用图象表示如图.则小明打了6分钟需付费 元.
三、计算题
12.(图1)中的摩天轮可抽象成一个圆,圆上一点离地面的高度与旋转时间 之间的关系如(图2)所示.
(1)根据(图2)填表:
0 3 6 8 …
…
(2)根据图中的信息,请写出摩天轮的直径.
13.在平面直角坐标系中,对于任意三点的“矩面积”,给出如下定义:“水平底”是任意两点横坐标差的最大值;“铅垂高”是任意两点纵坐标差的最大值,则“矩面积”.例如:三点的坐标分别为,则“水平底”,“铅垂高”,“矩面积”.根据所给定义解决下面的问题:
(1)若点的坐标分别为,求这三点的“矩面积”;
(2)若点,含有的式子表示这三点的“矩面积”(结果需化简);
(3)已知点,在轴上是否存在点,使这三点的“矩面积”为20?若存在,求出点的坐标;若不存在,请说明理由.
四、解答题
14.小明家、食堂、图书馆在同一条直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.小明离家的距离与时间之间的对应关系如图所示.
根据上图回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
(2)小明吃早餐用了多少时间?在图书馆停留了多少时间?
(3)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
五、作图题
15.已知二次函数
(1)完成下表;
(2)在如图的坐标系中描点,画出该二次函数的图象.
六、综合题
16.心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间有如下关系:(其中0≤x≤30)
提出概念所用时间(x) 2 5 7 10 12 13 14 17 20
对概念的接受能力(y) 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55
(1)上表中反映了哪两个变量之间的关系?
(2)当提出概念所用时间是10分钟时,学生的接受能力是多少?
(3)根据表格中的数据,你认为提出概念几分钟时,学生的接受能力最强;
(4)从表中可知,当时间x在什么范围内,学生的接受能力逐步增强?当时间x在什么范围内,学生的接受能力逐步降低?
17.由于惯性的作用,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号小型载客汽车的刹车性能(车速不超过),对这种型号的汽车进行了测试,测得的数据如下表:
刹车时车速 0 10 20 30 40 50 …
刹车距离 0 5 10 …
谛回答下列问题:
(1)当刹车时车速为时,刹车距离是_______m;
(2)根据上表反映的规律写出该种型号汽车s与v之间的关系式:_________;
(3)该型号汽车在高速公路上发生了一次交通事故,现场测得刹车距离为,推测刹车时车速是多少?并说明事故发生时,汽车是超速行驶还是正常行驶? (相关法规:《道路交通安全法》第七十八条:高速公路上行驶的小型载客汽车最高车速不得超过每小时120公里.)
18.人的大脑所能记忆的内容是有限的,随着时间的推移,记忆的内容逐渐被遗忘.德国心理学家艾宾浩威斯第一个发现了记忆遗忘规律,他根据自己研究得到的测试数据描绘了一条曲线(如图所示),这就是著名的艾宾浩威斯遗忘曲线,其中纵轴表示学习中的记忆保持量,横轴表示时间.观察图象并回答下列问题:
(1)学习后2h的时候,记忆保持量约是多少
(2)图中A点表示的实际意义是什么 在哪个时间段内遗忘的速度最快
(3)有研究表明,如及时复习,一天后能保持98%.根据遗忘曲线,如不复习,会有什么样的结果 小明说学习中能记住不过一会就忘了,都是因为自己笨.你同意他这样的说法吗 你会给他提出什么建议
答案解析部分
1.【答案】B
【知识点】函数的概念;函数的图象
2.【答案】C
【知识点】函数的图象
3.【答案】C
【知识点】函数的图象
4.【答案】C
【知识点】函数的图象
5.【答案】A
【知识点】函数的图象
6.【答案】224
【知识点】函数的表示方法
7.【答案】④②
【知识点】函数的图象
8.【答案】5
【知识点】分段函数
9.【答案】列表法;解析式法;图象法
【知识点】函数的表示方法
10.【答案】表格法;关系式法;图象法
【知识点】函数的表示方法
11.【答案】1.8
【知识点】分段函数
12.【答案】(1)解:结合图象填表如下:
x(min) 0 3 6 8 …
y(m) 5 70 5 54 …
(2)解:∵最高点为70米,最低点为5米,
∴摩天轮的直径为65米.
【知识点】函数的图象
13.【答案】解:(1)∵点D(-1,2)、E(2,-1)、F(0,6),如图:
∴,,
∴,
(2)∵点D(2,3)、E(2,-1)、F(t,-2),
∵D,E两点的横坐标相同,
∴,,
∴,
当时,,
当时,,
综上可得:;
(3)设点F的坐标为(,0),
∵点D(-1,2)、E(2,-2)、F(,0),
∴,
当点F在点D左侧,即x<-1时,如图:
则,
∴,故.
解得:,
∴点F的坐标为(,0).
当点F在点D、E之间,即-1
∴点F在点D、E之间时,不存在点F,使这三点的“矩面积”S为20.
当点F在点E右侧时,即x>2时,如图:
则,
∴,故.
解得:x=4,
∴点F的坐标为(,0).
综上,当点F的坐标为(,0)或(,0)时,这三点的“矩面积”为20.
【知识点】坐标与图形性质;分段函数
14.【答案】(1),
(2),
(3),
【知识点】函数的图象
15.【答案】(1)解:完成表格如下:
0 1 2 3 4
0
(2)解:描点,画出该二次函数图象如下:
【知识点】函数值;描点法画函数图象
16.【答案】(1)解:提出概念所用时间x和提出概念的接受能力y两个变量
(2)解:当x=10时,y=59,所以时间是10分钟,学生的接受能力是59
(3)解:当x=13时,y的值最大是59.9,所以提出概念13分钟时,学生的接受能力最强
(4)解:由表中数据可知:当2
【知识点】常量、变量;函数的表示方法
17.【答案】(1)
(2)
(3)推测刹车时车速是,所以事故发生时,汽车是超速行驶.
【知识点】函数解析式;函数自变量的取值范围;函数的表示方法
18.【答案】(1)解:由图可知,学习后2h的时候﹐记忆保持量约是40%;
(2)解:图中A点表示的实际意义是学习后15时的记忆保持量约为35%.在0-2h时间段内遗忘的速度最快
(3)解:如不复习﹐会很快忘掉很多﹐只能保持大约30%的记忆保持量;不同意小明的说法,记不住并不是因为笨﹐而是没有及时做好复习﹐建议在学习的一天内及时进行或多次复习(言之有理即可).
【知识点】函数的图象
21世纪教育网(www.21cnjy.com)
2 / 10
