19.1变量与函数(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
19.1变量与函数
一、单选题
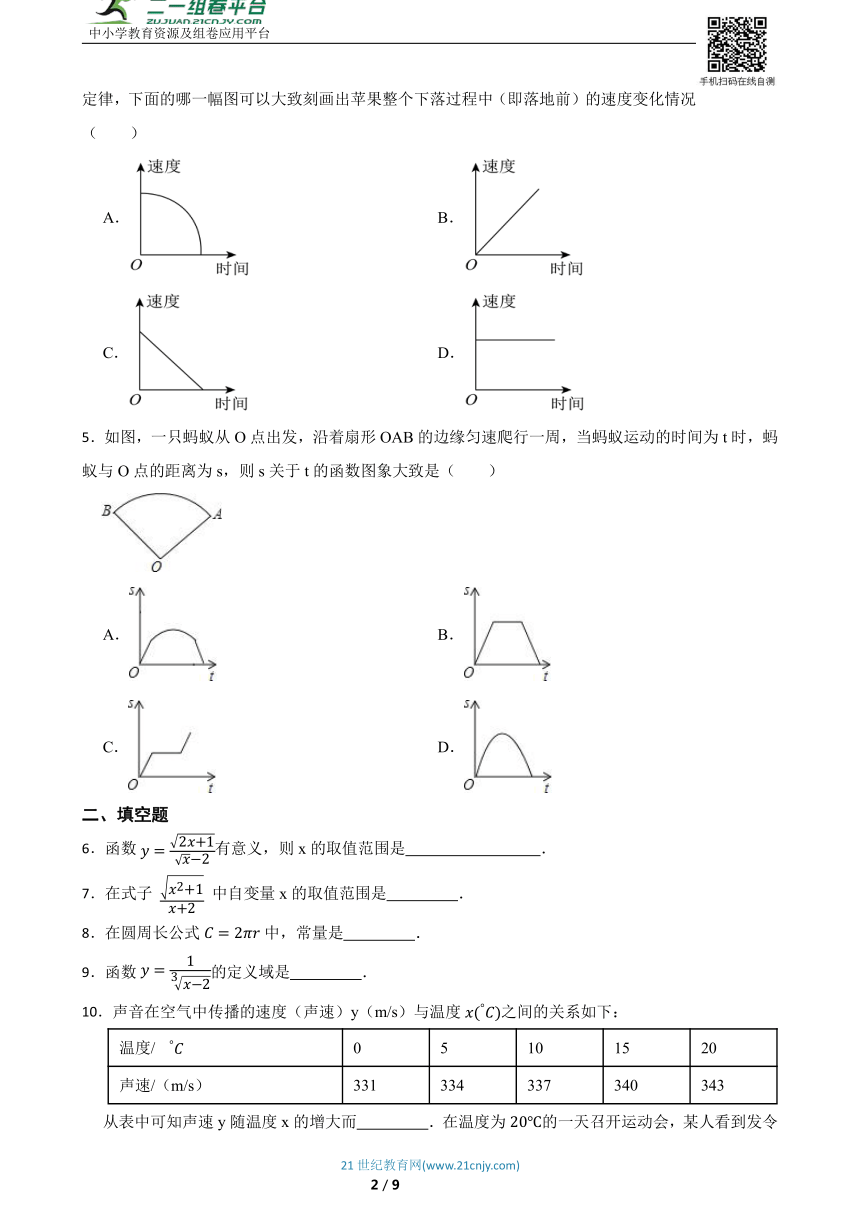
1.小明去帮妈妈买菜,从家中出发走分钟到一个离家米的菜市场,买菜花了分钟,之后用分钟返回家里,下面图形表示小明离家距离(米)与外出时间(分钟)之间关系图象的是( )
A. B.
C. D.
2.下列各图表示y是x的函数的图象是( )
A. B.
C. D.
3.下列各图中,表示y是x的函数的是( )
A. B.
C. D.
4.1687年,牛顿通过观察苹果落地的现象,发现任何物体之间都有相互吸引力,从而提出万有引力定律,下面的哪一幅图可以大致刻画出苹果整个下落过程中(即落地前)的速度变化情况( )
A. B.
C. D.
5.如图,一只蚂蚁从O点出发,沿着扇形OAB的边缘匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( )
A. B.
C. D.
二、填空题
6.函数有意义,则x的取值范围是 .
7.在式子 中自变量x的取值范围是 .
8.在圆周长公式中,常量是 .
9.函数的定义域是 .
10.声音在空气中传播的速度(声速)y(m/s)与温度之间的关系如下:
温度/ 0 5 10 15 20
声速/(m/s) 331 334 337 340 343
从表中可知声速y随温度x的增大而 .在温度为的一天召开运动会,某人看到发令枪的烟0.2s后,听到了枪声,则由此可知,这个人距离发令枪 m.
11.面对全球淡水资源日益减少的现状,倡导全民节约用水.若拧不紧的水龙头每秒钟滴两滴水,每滴水约0.05毫升,则浪费的水y(毫升)与时间x(秒)之间的关系式是 .
三、计算题
12.为了鼓励居民节约用水,某市采用“阶梯水价”的方法按月计算每户家庭的水费.每月用水量不超过20吨时,按每吨3元计费;每月用水量超过20吨时,其中的20吨仍按每吨3元计费,超过部分按每吨3.2元计费.设每户家庭月用水量为x吨时,应缴水费y元.
(1)分别求出和时,y与x之间的函数关系式;
(2)小颖家四月份、五月份分别缴水费63.2元、57元,则小颖家五月份比四月份节约用水多少吨
13.根据以下素材.探索完成任务.
杨梅季将至,梅企与某快递公司合作寄送杨梅.
素材1 某快递公司规定: 1.从当地寄送杨梅到A市按重量收费:当杨梅重量不超过10千克时,需要寄送费32元;当重量超过10千克时,超过部分另收m元/千克. 2.寄送杨梅重量均为整数千克.
素材2 电子存单1托寄物:杨梅 包装服务 产品类型:某快递公司 计量重量:7千克 件数:1 总费用:32元
电子存单2托寄物:杨梅 包装服务 产品类型:某快递公司 计量重量:12千克 件数:1 总费用:44元
电子存单3托寄物:杨梅 包装服务 产品类型:某快递公司 计量重量:15千克 件数:1 总费用:62元
问题解决
任务1 分析变量关系 根据以上信息,请确定m的值,并求出杨梅重量超过10千克时寄送费用y(元)关于杨梅重量x(千克)之间的函数关系式.
任务2 计算最省费用 若杨梅重量达到25千克,请求出最省的寄送费用.
任务3 探索最大重量 小聪想在当地梅企购买一批价格为50元/千克的杨梅并全部寄送给在A市的朋友们,若小聪能用来支配的钱有5000元,他最多可以购买多少千克的杨梅?并写出一种寄送方式.
14.如图,等腰三角形中,,,动点从点出发,沿路线匀速运动,速度为,运动到点停止,设运动时间为,的面积为.
(1)求的面积.
(2)求等腰腰上的高.
(3)请分别求出在边、上运动时,的面积为与运动时间之间的函数关系式.
(4)是否存在某一时刻,使得的面积正好是面积的,若存在,求出的值;若不存在,说明理由.
(5)当运动时间为_______时,(直接填空)为直角三角形.
四、解答题
15.一个蓄水池有水,打开放水闸门放水,水池里的水和放水时间的关系如表,回答下面问题:
放水时间(分钟) 1 2 3 4 5 …
水池中水量 48 46 42 40 …
(1)如图所示,将表格补充完整; .
(2)根据表格中的数据,说明在放完水前,水池中水量是随放水时间的增长而怎样变化的?
(3)当放水时间为7分钟时,水池中水量是多少立方米?
五、作图题
16.已知二次函数
(1)完成下表;
(2)在如图的坐标系中描点,画出该二次函数的图象.
六、综合题
17.随着科学技术的不断发展,电动汽车成为人们日常出行的重要交通工具,电动汽车的电池容量与续航里程成为人们最为关心的问题.现对某型号电动汽车充满电后进行测试,其电池剩余电量(度)与行驶里程(千米)之间的关系如下表所示:
行驶里程(千米) 0 10 20 40 …
剩余电量(度) 80 78 76 72 …
(1)表中自变量是________,因变量是__________.
(2)该型号电动汽车的电池容量为______度;
(3)请根据表中直接写出该电动汽车剩余电量(度)与行驶里程(千米)之间的关系式;
(4)求剩余电量为时电动汽车的行驶里程.
18.开始工作后一台拖拉机在开始工作前,油箱中有油,开始工作后,每小时耗油.
(1)写出油箱中的剩余油量与工作时间之间的关系式;
(2)当油箱内剩余的油量为时,这台拖拉机已工作了几个小时?
19.由于惯性的作用,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”.为了测定某种型号小型载客汽车的刹车性能(车速不超过),对这种型号的汽车进行了测试,测得的数据如下表:
刹车时车速 0 10 20 30 40 50 ……
刹车距离 0 2.5 5 7.5 10 12.5 ……
请回答下列问题:
(1)在这个变化过程中,自变量是______,因变量是______;
(2)当刹车时车速为时,刹车距离是______;
(3)该型号汽车在高速公路上发生了一次交通事故,现场测得刹车距离为,推测刹车时车速是多少?并说明事故发生时,汽车是超速行驶还是正常行驶?(相关法规:《道路交通安全法》第七十八条:高速公路上行驶的小型载客汽车最高车速不得超过.
七、实践探究题
20.综合与实践
综合实践小组探究香燃烧时剩余长度与燃烧时间x(分)的关系.下面表格是他们实验过程中的相关数据,请利用表格中的信息解答下列问题:
(1)将表格中空缺的数据补充完整:
燃烧时间x/分 0 5 10 15
剩余长度 20 16 ______ 8
(2)根据表中信息,分析香燃烧过程中剩余长度随燃烧时间x(分)的变化规律(写出一个结论即可);
(3)求香的剩余长度与燃烧时间x(分)之间的关系式,并求这只香多长时间后全部燃尽.
答案解析部分
1.【答案】B
【知识点】函数的图象
2.【答案】D
【知识点】函数的图象
3.【答案】A
【知识点】函数的概念
4.【答案】B
【知识点】用图象表示变量间的关系
5.【答案】B
【知识点】函数的图象
6.【答案】且
【知识点】分式有无意义的条件;二次根式有意义的条件;函数自变量的取值范围
7.【答案】x≠﹣2
【知识点】函数自变量的取值范围
8.【答案】2π
【知识点】常量、变量
9.【答案】
【知识点】分式有无意义的条件;函数自变量的取值范围;立方根的概念与表示
10.【答案】增大;
【知识点】用表格表示变量间的关系
11.【答案】
【知识点】函数解析式
12.【答案】(1)当时,;当时,
(2)小颖家五月份比四月份节约用水2吨
【知识点】一元一次方程的实际应用-计费问题;用关系式表示变量间的关系
13.【答案】(1);(2)元;(3)小聪最多可以购买杨梅,寄送方式为8件,1件.
【知识点】一元一次方程的其他应用;一元一次不等式的应用;用关系式表示变量间的关系
14.【答案】(1)
(2)等腰腰上的高为;
(3)
(4)满足条件的或;
(5)或8
【知识点】函数解析式;等腰三角形的判定与性质;勾股定理
15.【答案】(1)44
(2)解:水池中水量随放水时间的增长而减少.
(3)解:,
答:当放水时间为7分镫时,水池中水量是.
【知识点】用表格表示变量间的关系
16.【答案】(1)解:完成表格如下:
0 1 2 3 4
0
(2)解:描点,画出该二次函数图象如下:
【知识点】函数值;描点法画函数图象
17.【答案】(1)行驶里程(千米);剩余电量(度)
(2)80
(3)
(4)300千米
【知识点】函数自变量的取值范围;用表格表示变量间的关系;用关系式表示变量间的关系
18.【答案】(1)
(2)工作了5个小时
【知识点】函数自变量的取值范围;用关系式表示变量间的关系
19.【答案】(1)刹车时车速;刹车距离
(2)15
(3),超速行驶
【知识点】函数的概念;函数解析式;函数自变量的取值范围
20.【答案】(1)12
(2)香燃烧过程中剩余长度随燃烧时间x(分)的增加而减少
(3),这只香25分钟后全部燃尽
【知识点】函数自变量的取值范围;用表格表示变量间的关系;用关系式表示变量间的关系
21世纪教育网(www.21cnjy.com)
1 / 9
19.1变量与函数
一、单选题
1.小明去帮妈妈买菜,从家中出发走分钟到一个离家米的菜市场,买菜花了分钟,之后用分钟返回家里,下面图形表示小明离家距离(米)与外出时间(分钟)之间关系图象的是( )
A. B.
C. D.
2.下列各图表示y是x的函数的图象是( )
A. B.
C. D.
3.下列各图中,表示y是x的函数的是( )
A. B.
C. D.
4.1687年,牛顿通过观察苹果落地的现象,发现任何物体之间都有相互吸引力,从而提出万有引力定律,下面的哪一幅图可以大致刻画出苹果整个下落过程中(即落地前)的速度变化情况( )
A. B.
C. D.
5.如图,一只蚂蚁从O点出发,沿着扇形OAB的边缘匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( )
A. B.
C. D.
二、填空题
6.函数有意义,则x的取值范围是 .
7.在式子 中自变量x的取值范围是 .
8.在圆周长公式中,常量是 .
9.函数的定义域是 .
10.声音在空气中传播的速度(声速)y(m/s)与温度之间的关系如下:
温度/ 0 5 10 15 20
声速/(m/s) 331 334 337 340 343
从表中可知声速y随温度x的增大而 .在温度为的一天召开运动会,某人看到发令枪的烟0.2s后,听到了枪声,则由此可知,这个人距离发令枪 m.
11.面对全球淡水资源日益减少的现状,倡导全民节约用水.若拧不紧的水龙头每秒钟滴两滴水,每滴水约0.05毫升,则浪费的水y(毫升)与时间x(秒)之间的关系式是 .
三、计算题
12.为了鼓励居民节约用水,某市采用“阶梯水价”的方法按月计算每户家庭的水费.每月用水量不超过20吨时,按每吨3元计费;每月用水量超过20吨时,其中的20吨仍按每吨3元计费,超过部分按每吨3.2元计费.设每户家庭月用水量为x吨时,应缴水费y元.
(1)分别求出和时,y与x之间的函数关系式;
(2)小颖家四月份、五月份分别缴水费63.2元、57元,则小颖家五月份比四月份节约用水多少吨
13.根据以下素材.探索完成任务.
杨梅季将至,梅企与某快递公司合作寄送杨梅.
素材1 某快递公司规定: 1.从当地寄送杨梅到A市按重量收费:当杨梅重量不超过10千克时,需要寄送费32元;当重量超过10千克时,超过部分另收m元/千克. 2.寄送杨梅重量均为整数千克.
素材2 电子存单1托寄物:杨梅 包装服务 产品类型:某快递公司 计量重量:7千克 件数:1 总费用:32元
电子存单2托寄物:杨梅 包装服务 产品类型:某快递公司 计量重量:12千克 件数:1 总费用:44元
电子存单3托寄物:杨梅 包装服务 产品类型:某快递公司 计量重量:15千克 件数:1 总费用:62元
问题解决
任务1 分析变量关系 根据以上信息,请确定m的值,并求出杨梅重量超过10千克时寄送费用y(元)关于杨梅重量x(千克)之间的函数关系式.
任务2 计算最省费用 若杨梅重量达到25千克,请求出最省的寄送费用.
任务3 探索最大重量 小聪想在当地梅企购买一批价格为50元/千克的杨梅并全部寄送给在A市的朋友们,若小聪能用来支配的钱有5000元,他最多可以购买多少千克的杨梅?并写出一种寄送方式.
14.如图,等腰三角形中,,,动点从点出发,沿路线匀速运动,速度为,运动到点停止,设运动时间为,的面积为.
(1)求的面积.
(2)求等腰腰上的高.
(3)请分别求出在边、上运动时,的面积为与运动时间之间的函数关系式.
(4)是否存在某一时刻,使得的面积正好是面积的,若存在,求出的值;若不存在,说明理由.
(5)当运动时间为_______时,(直接填空)为直角三角形.
四、解答题
15.一个蓄水池有水,打开放水闸门放水,水池里的水和放水时间的关系如表,回答下面问题:
放水时间(分钟) 1 2 3 4 5 …
水池中水量 48 46 42 40 …
(1)如图所示,将表格补充完整; .
(2)根据表格中的数据,说明在放完水前,水池中水量是随放水时间的增长而怎样变化的?
(3)当放水时间为7分钟时,水池中水量是多少立方米?
五、作图题
16.已知二次函数
(1)完成下表;
(2)在如图的坐标系中描点,画出该二次函数的图象.
六、综合题
17.随着科学技术的不断发展,电动汽车成为人们日常出行的重要交通工具,电动汽车的电池容量与续航里程成为人们最为关心的问题.现对某型号电动汽车充满电后进行测试,其电池剩余电量(度)与行驶里程(千米)之间的关系如下表所示:
行驶里程(千米) 0 10 20 40 …
剩余电量(度) 80 78 76 72 …
(1)表中自变量是________,因变量是__________.
(2)该型号电动汽车的电池容量为______度;
(3)请根据表中直接写出该电动汽车剩余电量(度)与行驶里程(千米)之间的关系式;
(4)求剩余电量为时电动汽车的行驶里程.
18.开始工作后一台拖拉机在开始工作前,油箱中有油,开始工作后,每小时耗油.
(1)写出油箱中的剩余油量与工作时间之间的关系式;
(2)当油箱内剩余的油量为时,这台拖拉机已工作了几个小时?
19.由于惯性的作用,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”.为了测定某种型号小型载客汽车的刹车性能(车速不超过),对这种型号的汽车进行了测试,测得的数据如下表:
刹车时车速 0 10 20 30 40 50 ……
刹车距离 0 2.5 5 7.5 10 12.5 ……
请回答下列问题:
(1)在这个变化过程中,自变量是______,因变量是______;
(2)当刹车时车速为时,刹车距离是______;
(3)该型号汽车在高速公路上发生了一次交通事故,现场测得刹车距离为,推测刹车时车速是多少?并说明事故发生时,汽车是超速行驶还是正常行驶?(相关法规:《道路交通安全法》第七十八条:高速公路上行驶的小型载客汽车最高车速不得超过.
七、实践探究题
20.综合与实践
综合实践小组探究香燃烧时剩余长度与燃烧时间x(分)的关系.下面表格是他们实验过程中的相关数据,请利用表格中的信息解答下列问题:
(1)将表格中空缺的数据补充完整:
燃烧时间x/分 0 5 10 15
剩余长度 20 16 ______ 8
(2)根据表中信息,分析香燃烧过程中剩余长度随燃烧时间x(分)的变化规律(写出一个结论即可);
(3)求香的剩余长度与燃烧时间x(分)之间的关系式,并求这只香多长时间后全部燃尽.
答案解析部分
1.【答案】B
【知识点】函数的图象
2.【答案】D
【知识点】函数的图象
3.【答案】A
【知识点】函数的概念
4.【答案】B
【知识点】用图象表示变量间的关系
5.【答案】B
【知识点】函数的图象
6.【答案】且
【知识点】分式有无意义的条件;二次根式有意义的条件;函数自变量的取值范围
7.【答案】x≠﹣2
【知识点】函数自变量的取值范围
8.【答案】2π
【知识点】常量、变量
9.【答案】
【知识点】分式有无意义的条件;函数自变量的取值范围;立方根的概念与表示
10.【答案】增大;
【知识点】用表格表示变量间的关系
11.【答案】
【知识点】函数解析式
12.【答案】(1)当时,;当时,
(2)小颖家五月份比四月份节约用水2吨
【知识点】一元一次方程的实际应用-计费问题;用关系式表示变量间的关系
13.【答案】(1);(2)元;(3)小聪最多可以购买杨梅,寄送方式为8件,1件.
【知识点】一元一次方程的其他应用;一元一次不等式的应用;用关系式表示变量间的关系
14.【答案】(1)
(2)等腰腰上的高为;
(3)
(4)满足条件的或;
(5)或8
【知识点】函数解析式;等腰三角形的判定与性质;勾股定理
15.【答案】(1)44
(2)解:水池中水量随放水时间的增长而减少.
(3)解:,
答:当放水时间为7分镫时,水池中水量是.
【知识点】用表格表示变量间的关系
16.【答案】(1)解:完成表格如下:
0 1 2 3 4
0
(2)解:描点,画出该二次函数图象如下:
【知识点】函数值;描点法画函数图象
17.【答案】(1)行驶里程(千米);剩余电量(度)
(2)80
(3)
(4)300千米
【知识点】函数自变量的取值范围;用表格表示变量间的关系;用关系式表示变量间的关系
18.【答案】(1)
(2)工作了5个小时
【知识点】函数自变量的取值范围;用关系式表示变量间的关系
19.【答案】(1)刹车时车速;刹车距离
(2)15
(3),超速行驶
【知识点】函数的概念;函数解析式;函数自变量的取值范围
20.【答案】(1)12
(2)香燃烧过程中剩余长度随燃烧时间x(分)的增加而减少
(3),这只香25分钟后全部燃尽
【知识点】函数自变量的取值范围;用表格表示变量间的关系;用关系式表示变量间的关系
21世纪教育网(www.21cnjy.com)
1 / 9
