19.2.3 一次函数与方程 ,不等式(含答案)
文档属性
| 名称 | 19.2.3 一次函数与方程 ,不等式(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 670.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-21 00:00:00 | ||
图片预览

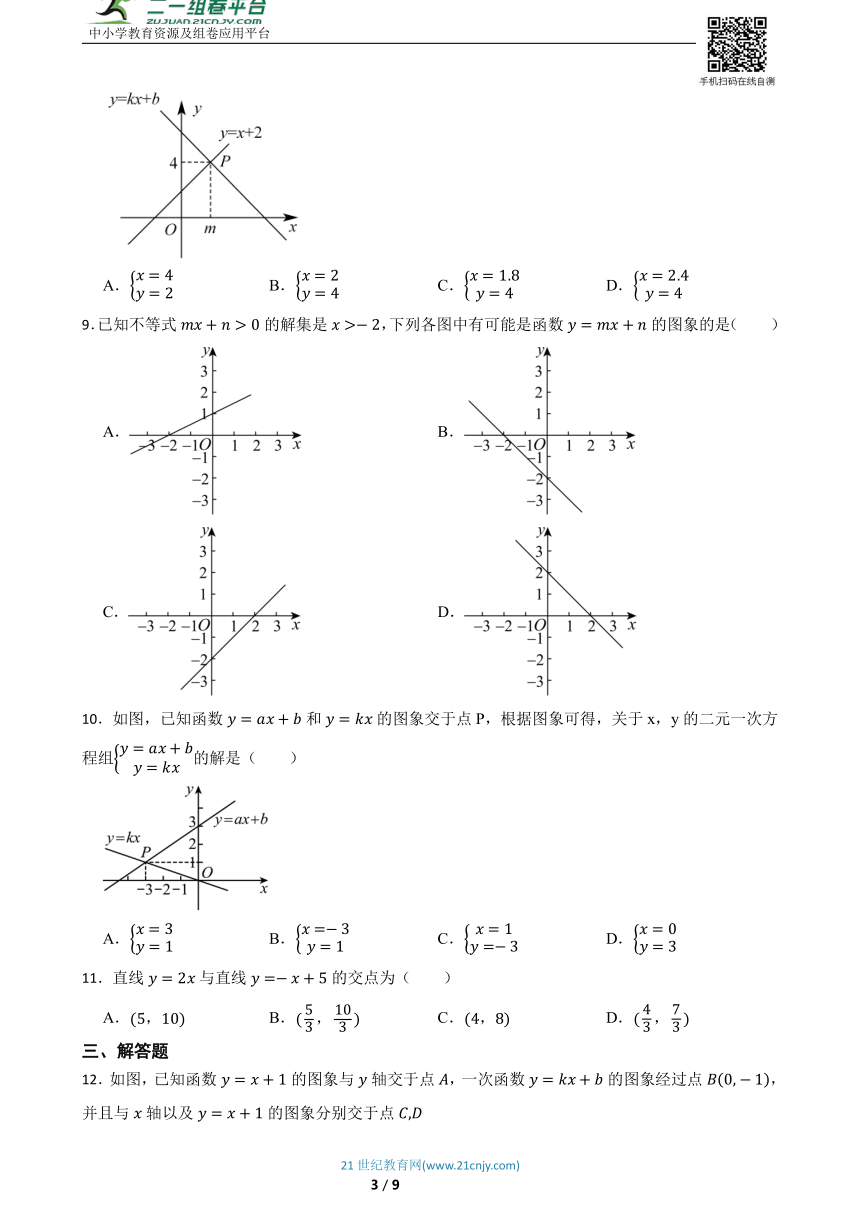

文档简介
中小学教育资源及组卷应用平台
19.2.3 一次函数与方程 ,不等式
一、填空题
1.直线与,两条直线与轴都交于点,且它们与轴围成的三角形面积为,则 .
2.直线:与直线:在同一平面直角坐标系中的图象如图所示,则关于x的不等式的解集为 .
3.如图,函数和的图象交于,两点,当时,的取值范围为 .
4.如图,一次函数y=kx+b与正比例函数y=2x的图象交于点A,且与y轴交于点B,则一次函数y=2x-1与y=kx+b的图象交点坐标为 .
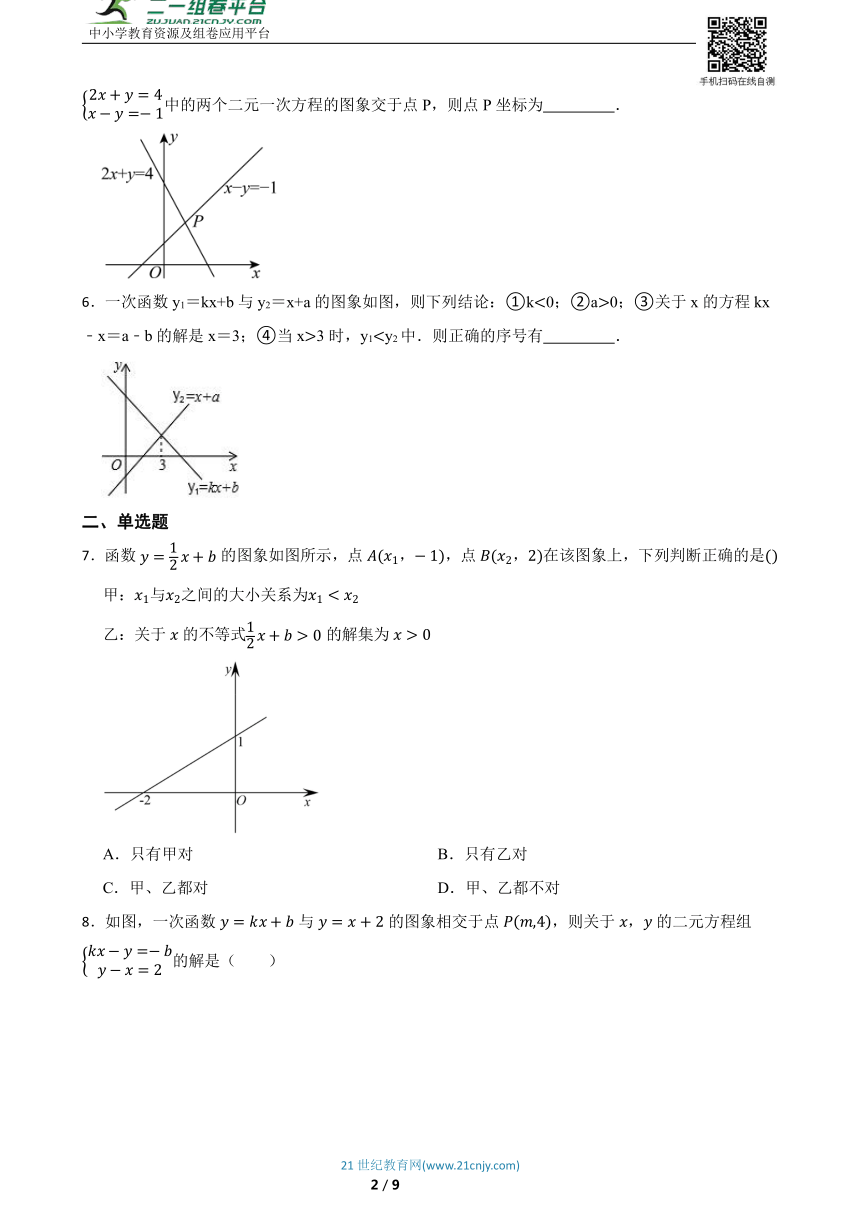
5.以二元一次方程的解为坐标的点的全体叫做这个二元一次方程的图象.如图,二元一次方程组中的两个二元一次方程的图象交于点P,则点P坐标为 .
6.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k0;②a0;③关于x的方程kx﹣x=a﹣b的解是x=3;④当x3时,y1y2中.则正确的序号有 .
二、单选题
7.函数的图象如图所示,点,,点,在该图象上,下列判断正确的是
甲:与之间的大小关系为
乙:关于的不等式的解集为
A.只有甲对 B.只有乙对
C.甲、乙都对 D.甲、乙都不对
8.如图,一次函数与的图象相交于点,则关于,的二元方程组的解是( )
A. B. C. D.
9.已知不等式的解集是,下列各图中有可能是函数的图象的是( )
A. B.
C. D.
10.如图,已知函数和的图象交于点P,根据图象可得,关于x,y的二元一次方程组的解是( )
A. B. C. D.
11.直线与直线的交点为( )
A. B. C. D.
三、解答题
12.如图,已知函数的图象与轴交于点,一次函数的图象经过点,并且与轴以及的图象分别交于点
(1)若点的横坐标为,求一次函数的解析式;
(2)求四边形的面积(即图中阴影部分的面积).
四、计算题
13.如图,直线经过点,.
(1)求直线的解析式;
(2)若直线与直线相交于点C,求点C的坐标;
(3)根据图像,写出关于x的不等式的解集.
14.如图,在平面直角坐标系中,函数的图象交x轴于点A、交y轴于点B,函数(m为常数)的图象为直线,交x轴于点C、交y轴于点D,直线与直线相交于点P.
(1)点A的坐标为__________,点B的坐标为_________.
(2)当时,求点P的坐标.
(3)当点P位于第四象限时,求m的取值范围.
(4)连结,,当的面积是面积的2倍时,直接写出m的值.
五、作图题
15.画出函数的图象,利用图象:
(1)求方程的解;
(2)求不等式的解集;
(3)若,求x的取值范围.
六、综合题
16.已知函数 和 的图象交于点
(1)求 的值
(2)求 与两坐标轴围成的面积.
17.如图,直线 与直线 分别与x轴交于点A、B,两直线交于点C.
(1)求 的面积;
(2)利用图象直接写出当x取何值时, .
18.已知甲、乙两地相距840千米,客车、货车分别从甲、乙两地同时出发,匀速相向行驶.货车2小时可到达途中丙站,客车需9小时到达丙站(如图1所示),货车的速度是客车的 ,客、货车到丙站的距离分别为 、 (千米),它们与行驶时间x(时间)之间的函数关系如图2所示.
(1)求客、货两车的速度;
(2)如图2,两函数图象交于点E,求E点坐标.
七、实践探究题
19.如图,直线与轴、轴分别交于点,.点的坐标为,点的坐标为.
(1)求的值,及一次函数解析式;
(2)若点是第二象限内的直线上的一个动点.当点运动过程中,试写出的面积与的函数关系式,并写出自变量的取值范围;
(3)探究:当运动到什么位置时,的面积为,并说明理由.
答案解析部分
1.【答案】
【知识点】一次函数图象与坐标轴交点问题
2.【答案】
【知识点】一次函数与不等式(组)的关系
3.【答案】
【知识点】一次函数与不等式(组)的关系
4.【答案】,
【知识点】一次函数与二元一次方程(组)的关系
5.【答案】
【知识点】一次函数与二元一次方程(组)的关系
6.【答案】①③④
【知识点】一次函数与不等式(组)的关系
7.【答案】A
【知识点】一次函数与不等式(组)的关系;一次函数的性质
8.【答案】B
【知识点】一次函数与二元一次方程(组)的关系
9.【答案】A
【知识点】一次函数与不等式(组)的关系
10.【答案】B
【知识点】一次函数与二元一次方程(组)的关系
11.【答案】B
【知识点】两一次函数图象相交或平行问题
12.【答案】(1);(2)
【知识点】待定系数法求一次函数解析式;一次函数与二元一次方程(组)的关系
13.【答案】(1)直线的解析式为
(2)点C的坐标为
(3)
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;一次函数与二元一次方程(组)的关系
14.【答案】(1),
(2)点P的坐标为
(3)
(4)或
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;一次函数与二元一次方程(组)的关系;一次函数图象与坐标轴交点问题
15.【答案】(1)
(2)
(3)
【知识点】一次函数的图象;一次函数与一元一次方程的关系;一次函数与不等式(组)的关系;一次函数图象与坐标轴交点问题
16.【答案】(1)解:把(a,6)代入 得 ,
把(2,6)代入 得:
,
解得: ,
∴ , ;
(2)解:由(1)可知一次函数为 ,
令 ,则 ,
解得: ,
∴直线 与 轴交于( ,0),与 轴交于 ,
∴ 与两坐标轴围成的面积 .
【知识点】两一次函数图象相交或平行问题;一次函数图象与坐标轴交点问题
17.【答案】(1)解:把 代入 中得: ,
解得: ,所以
把 代入 中得: ,
解得: ,所以 .
.
解方程 ,得 ,
把 代入 中得: ,
所以 ,
所以 .
(2)解:由图可知交点C的右边y1即当 时,
【知识点】三角形的面积;一次函数图象与坐标轴交点问题
18.【答案】(1)解:设客车的速度是x千米/小时,则货车的速度为 千米/小时,
依题意可得: ,
解得 ,
∴ ,
答:客车的速度是80千米/小时,货车的速度是60千米/小时;
(2)解:由题意可知:
当 时, 过点 , ,
当 时 过点 , ,
设 , 有
解得
∴ ,
联立两式,解得
∴点E的坐标为
【知识点】两一次函数图象相交或平行问题;一元一次方程的实际应用-行程问题
19.【答案】(1),
(2)
(3),或,
【知识点】待定系数法求一次函数解析式;一次函数图象与坐标轴交点问题
21世纪教育网(www.21cnjy.com)
2 / 9
19.2.3 一次函数与方程 ,不等式
一、填空题
1.直线与,两条直线与轴都交于点,且它们与轴围成的三角形面积为,则 .
2.直线:与直线:在同一平面直角坐标系中的图象如图所示,则关于x的不等式的解集为 .
3.如图,函数和的图象交于,两点,当时,的取值范围为 .
4.如图,一次函数y=kx+b与正比例函数y=2x的图象交于点A,且与y轴交于点B,则一次函数y=2x-1与y=kx+b的图象交点坐标为 .
5.以二元一次方程的解为坐标的点的全体叫做这个二元一次方程的图象.如图,二元一次方程组中的两个二元一次方程的图象交于点P,则点P坐标为 .
6.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k0;②a0;③关于x的方程kx﹣x=a﹣b的解是x=3;④当x3时,y1y2中.则正确的序号有 .
二、单选题
7.函数的图象如图所示,点,,点,在该图象上,下列判断正确的是
甲:与之间的大小关系为
乙:关于的不等式的解集为
A.只有甲对 B.只有乙对
C.甲、乙都对 D.甲、乙都不对
8.如图,一次函数与的图象相交于点,则关于,的二元方程组的解是( )
A. B. C. D.
9.已知不等式的解集是,下列各图中有可能是函数的图象的是( )
A. B.
C. D.
10.如图,已知函数和的图象交于点P,根据图象可得,关于x,y的二元一次方程组的解是( )
A. B. C. D.
11.直线与直线的交点为( )
A. B. C. D.
三、解答题
12.如图,已知函数的图象与轴交于点,一次函数的图象经过点,并且与轴以及的图象分别交于点
(1)若点的横坐标为,求一次函数的解析式;
(2)求四边形的面积(即图中阴影部分的面积).
四、计算题
13.如图,直线经过点,.
(1)求直线的解析式;
(2)若直线与直线相交于点C,求点C的坐标;
(3)根据图像,写出关于x的不等式的解集.
14.如图,在平面直角坐标系中,函数的图象交x轴于点A、交y轴于点B,函数(m为常数)的图象为直线,交x轴于点C、交y轴于点D,直线与直线相交于点P.
(1)点A的坐标为__________,点B的坐标为_________.
(2)当时,求点P的坐标.
(3)当点P位于第四象限时,求m的取值范围.
(4)连结,,当的面积是面积的2倍时,直接写出m的值.
五、作图题
15.画出函数的图象,利用图象:
(1)求方程的解;
(2)求不等式的解集;
(3)若,求x的取值范围.
六、综合题
16.已知函数 和 的图象交于点
(1)求 的值
(2)求 与两坐标轴围成的面积.
17.如图,直线 与直线 分别与x轴交于点A、B,两直线交于点C.
(1)求 的面积;
(2)利用图象直接写出当x取何值时, .
18.已知甲、乙两地相距840千米,客车、货车分别从甲、乙两地同时出发,匀速相向行驶.货车2小时可到达途中丙站,客车需9小时到达丙站(如图1所示),货车的速度是客车的 ,客、货车到丙站的距离分别为 、 (千米),它们与行驶时间x(时间)之间的函数关系如图2所示.
(1)求客、货两车的速度;
(2)如图2,两函数图象交于点E,求E点坐标.
七、实践探究题
19.如图,直线与轴、轴分别交于点,.点的坐标为,点的坐标为.
(1)求的值,及一次函数解析式;
(2)若点是第二象限内的直线上的一个动点.当点运动过程中,试写出的面积与的函数关系式,并写出自变量的取值范围;
(3)探究:当运动到什么位置时,的面积为,并说明理由.
答案解析部分
1.【答案】
【知识点】一次函数图象与坐标轴交点问题
2.【答案】
【知识点】一次函数与不等式(组)的关系
3.【答案】
【知识点】一次函数与不等式(组)的关系
4.【答案】,
【知识点】一次函数与二元一次方程(组)的关系
5.【答案】
【知识点】一次函数与二元一次方程(组)的关系
6.【答案】①③④
【知识点】一次函数与不等式(组)的关系
7.【答案】A
【知识点】一次函数与不等式(组)的关系;一次函数的性质
8.【答案】B
【知识点】一次函数与二元一次方程(组)的关系
9.【答案】A
【知识点】一次函数与不等式(组)的关系
10.【答案】B
【知识点】一次函数与二元一次方程(组)的关系
11.【答案】B
【知识点】两一次函数图象相交或平行问题
12.【答案】(1);(2)
【知识点】待定系数法求一次函数解析式;一次函数与二元一次方程(组)的关系
13.【答案】(1)直线的解析式为
(2)点C的坐标为
(3)
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;一次函数与二元一次方程(组)的关系
14.【答案】(1),
(2)点P的坐标为
(3)
(4)或
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;一次函数与二元一次方程(组)的关系;一次函数图象与坐标轴交点问题
15.【答案】(1)
(2)
(3)
【知识点】一次函数的图象;一次函数与一元一次方程的关系;一次函数与不等式(组)的关系;一次函数图象与坐标轴交点问题
16.【答案】(1)解:把(a,6)代入 得 ,
把(2,6)代入 得:
,
解得: ,
∴ , ;
(2)解:由(1)可知一次函数为 ,
令 ,则 ,
解得: ,
∴直线 与 轴交于( ,0),与 轴交于 ,
∴ 与两坐标轴围成的面积 .
【知识点】两一次函数图象相交或平行问题;一次函数图象与坐标轴交点问题
17.【答案】(1)解:把 代入 中得: ,
解得: ,所以
把 代入 中得: ,
解得: ,所以 .
.
解方程 ,得 ,
把 代入 中得: ,
所以 ,
所以 .
(2)解:由图可知交点C的右边y1
【知识点】三角形的面积;一次函数图象与坐标轴交点问题
18.【答案】(1)解:设客车的速度是x千米/小时,则货车的速度为 千米/小时,
依题意可得: ,
解得 ,
∴ ,
答:客车的速度是80千米/小时,货车的速度是60千米/小时;
(2)解:由题意可知:
当 时, 过点 , ,
当 时 过点 , ,
设 , 有
解得
∴ ,
联立两式,解得
∴点E的坐标为
【知识点】两一次函数图象相交或平行问题;一元一次方程的实际应用-行程问题
19.【答案】(1),
(2)
(3),或,
【知识点】待定系数法求一次函数解析式;一次函数图象与坐标轴交点问题
21世纪教育网(www.21cnjy.com)
2 / 9
