19.3课题学习 选择方案(含答案)
文档属性
| 名称 | 19.3课题学习 选择方案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 185.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-21 16:23:54 | ||
图片预览


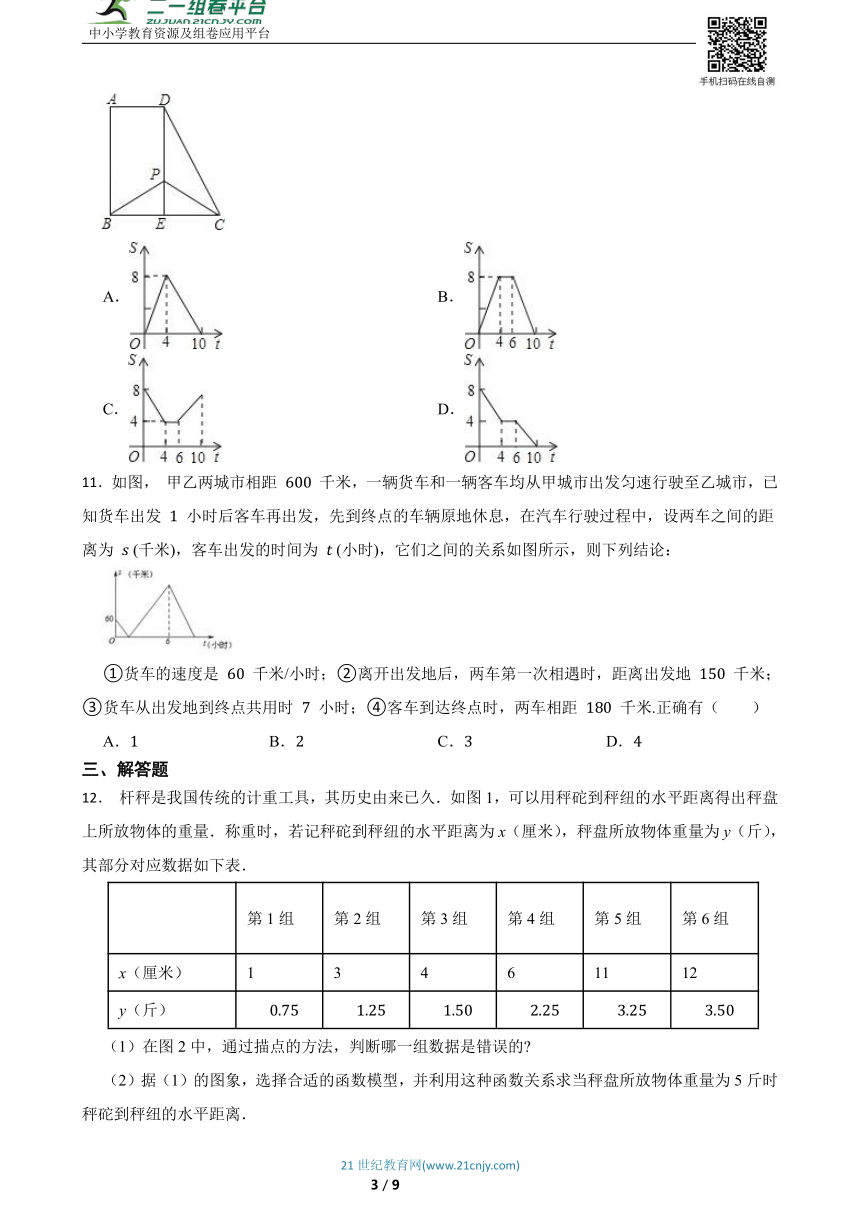

文档简介
中小学教育资源及组卷应用平台
19.3课题学习 选择方案
一、填空题
1.直线y= x+ 与x轴的交点坐标为 .
2.已知汽车装满油之后,油箱里的剩余油量y(升)与汽车行驶路程x(千米)之间的函数图象如图所示.为了行驶安全,油箱中的油量不能少于(升),那么这辆汽车装满油后至多行驶 (千米)后需要再次加油.
3.同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数解析式是y= x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为 ℃.
4.同一温度的华氏度数(℉)与摄氏度数(℃)之间的函数关系是,如果某一温度的摄氏度数是5℃,那么它的华氏度数是 ℉.
5.甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示.下列说法:①乙先到达青少年宫;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中正确的是 (填序号).
6.科学家研究发现声音在空气中传播的速度y(米/秒)与气温有的关系,若今天的气温是,则声音的传播速度是 米/秒.
二、单选题
7.据史书记载,漏刻是中国古代的一种计时工具,是古代人民对函数思想的创造性应用.研究发现水位 h(cm)与时间 t(min) 满足 h=0.4t+2,当 h 为 6cm时,时间 t 的值为( )
A.4.4min B.10min C.15min D.20min
8.在弹性限度内,弹簧挂上物体后会伸长,测得弹簧的长度与所挂物体的质量之间有如下关系:
0 1 2 3 4 5 …
10 10.5 11 11.5 12 12.5 …
在弹性限度内,所挂物体的质量为时,弹簧的长度为( )
A. B. C. D.
9.武汉市推出上网课包月制,每月收取上网课费用单位:元与上网时间单位:小时的函数关系如图所示若小明三月份在家上网课的费用为78元,则他三月份在家上网课的时间为( )
A.32小时 B.35小时 C.36小时 D.38小时
10.如图,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=BC=4,DE⊥BC于点E,且E是BC中点;动点P从点E出发沿路径ED→DA→AB以每秒1个单位长度的速度向终点B运动;设点P的运动时间为t秒,△PBC的面积为S,则下列能反映S与t的函数关系的图象是( )
A. B.
C. D.
11.如图, 甲乙两城市相距 千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市,已知货车出发 小时后客车再出发,先到终点的车辆原地休息,在汽车行驶过程中,设两车之间的距离为 (千米),客车出发的时间为 (小时),它们之间的关系如图所示,则下列结论:
①货车的速度是 千米/小时;②离开出发地后,两车第一次相遇时,距离出发地 千米;③货车从出发地到终点共用时 小时;④客车到达终点时,两车相距 千米.正确有( )
A. B. C. D.
三、解答题
12. 杆秤是我国传统的计重工具,其历史由来已久.如图1,可以用秤砣到秤纽的水平距离得出秤盘上所放物体的重量.称重时,若记秤砣到秤纽的水平距离为x(厘米),秤盘所放物体重量为y(斤),其部分对应数据如下表.
第1组 第2组 第3组 第4组 第5组 第6组
x(厘米) 1 3 4 6 11 12
y(斤)
(1)在图2中,通过描点的方法,判断哪一组数据是错误的
(2)据(1)的图象,选择合适的函数模型,并利用这种函数关系求当秤盘所放物体重量为5斤时秤砣到秤纽的水平距离.
四、计算题
13.1号探测气球从海拔5m出发,以1m/min的速度上升,与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升,两个气球都上升了1小时.
(1)用式子分别表示两个气球所在位置的海拔y(单位:m)关于上升时间t(单位:min)的函数关系;
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多少时间?位于什么高度?
五、综合题
14.“低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上下班.王叔叔某天骑自行车上班从家出发到单位过程中行进速度v(米/分钟)随时间t(分钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
(1)①当t=2分钟时,速度v= 米/分钟,路程s= 米;
②当t=15分钟时,速度v= 米/分钟,路程s= 米.
(2)当0≤t≤3和3<t≤15时,分别求出路程s(米)关于时间t(分钟)的函数解析式
(3)求王叔叔该天上班从家出发行进了750米时所用的时间t.
15.为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,2只A型节能灯和3只B型节能灯共需31元.
(1)求1只A型节能灯和1只B型节能灯的售价各是多少元?
(2)学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案,并说明理由.
16.随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 7 25 0.01
B m n 0.01
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
答案解析部分
1.【答案】(﹣4,0)
【知识点】一次函数的实际应用;一次函数的性质
2.【答案】
【知识点】一次函数的实际应用
3.【答案】-40
【知识点】一次函数的实际应用
4.【答案】41
【知识点】函数值;一次函数的实际应用
5.【答案】①②③
【知识点】一次函数的实际应用
6.【答案】342
【知识点】一次函数的实际应用
7.【答案】B
【知识点】一次函数的实际应用
8.【答案】C
【知识点】一次函数的实际应用
9.【答案】C
【知识点】一次函数的实际应用
10.【答案】B
【知识点】一次函数的实际应用
11.【答案】C
【知识点】一次函数的实际应用
12.【答案】(1)解:描点如图所示,
结合图形可知,除了第4组数据不同外,其他组数据均在图中的直线上,
故第4组数据是错误的;
(2)解:结合(1)上图可知,y(斤)与x(厘米)之间符合一次函数图象,
设y(斤)与x(厘米)之间的函数表达式为,
把,;,代入,
得,
解得:,
∴求y(斤)与x(厘米)之间的函数表达式为;
当时,,
解得:
∴当秤钩上所挂物重是5斤时,秤杆上秤砣到秤纽的水平距离是厘米;
【知识点】一次函数的实际应用;用表格表示变量间的关系;用图象表示变量间的关系
13.【答案】(1)解:根据题意得:1号探测气球所在位置的海拔:y1=t+5,2号探测气球所在位置的海拔:y2=0.5t+15;
(2)解:两个气球能位于同一高度,
根据题意得:t+5=0.5t+15,
解得:t=20,有t+5=25.
答:此时,气球上升了20分钟,都位于海拔25米的高度.
【知识点】一次函数的实际应用;列一次函数关系式
14.【答案】(1)200;200;300;4050
(2)解:①当0≤t≤3,设直线OA的解析式为:v=kt,由图象可知点A(3,300),
∴300=3k,
解得:k=100,
则解析式为:v=100t;
设l与OA的交点为P,则P(t,100t),
∴s=,
②当3<t≤15时,设l与AB的交点为Q,则Q(t,300),
∴S=
(3)解:∵当0≤t≤3,S最大=50×9=450,
∵750>450,
∴当3<t≤15时,450<S≤4050,
则令750=300t﹣450,
解得:t=4.
故王叔叔该天上班从家出发行进了750米时所用的时间4分钟.
【知识点】一次函数的实际应用
15.【答案】(1)解:设1只A型节能灯的售价是x元,1只B型节能灯的售价是y元,
,解得, ,
答:1只A型节能灯的售价是5元,1只B型节能灯的售价是7元
(2)解:设购买A型号的节能灯a只,则购买B型号的节能灯 只,费用为w元,
∴当 时,w取得最小值,此时
答:当购买A型号节能灯150只,B型号节能灯50只时最省钱
【知识点】一次函数的实际应用;二元一次方程组的实际应用-销售问题
16.【答案】(1)10;50
(2)解:yA与x之间的函数关系式为:
当x≤25时,yA=7,
当x>25时,yA=7+(x﹣25)×60×0.01,
∴yA=0.6x﹣8,
∴yA=;
(3)解:∵yB与x之间函数关系为:当x≤50时,yB=10,
当x>50时,yB=10+(x﹣50)×60×0.01=0.6x﹣20,
当0<x≤25时,yA=7,yB=50,
∴yA<yB,
∴选择A方式上网学习合算,
当25<x≤50时.yA=yB,即0.6x﹣8=10,解得;x=30,
∴当25<x<30时,yA<yB,选择A方式上网学习合算,
当x=30时,yA=yB,选择哪种方式上网学习都行,
当30<x≤50,yA>yB,选择B方式上网学习合算,
当x>50时,∵yA=0.6x﹣8,yB=0.6x﹣20,yA>yB,∴选择B方式上网学习合算,
综上所述:当0<x<30时,yA<yB,选择A方式上网学习合算,
当x=30时,yA=yB,选择哪种方式上网学习都行,
当x>30时,yA>yB,选择B方式上网学习合算.
【知识点】一次函数的实际应用
21世纪教育网(www.21cnjy.com)
2 / 9
19.3课题学习 选择方案
一、填空题
1.直线y= x+ 与x轴的交点坐标为 .
2.已知汽车装满油之后,油箱里的剩余油量y(升)与汽车行驶路程x(千米)之间的函数图象如图所示.为了行驶安全,油箱中的油量不能少于(升),那么这辆汽车装满油后至多行驶 (千米)后需要再次加油.
3.同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数解析式是y= x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为 ℃.
4.同一温度的华氏度数(℉)与摄氏度数(℃)之间的函数关系是,如果某一温度的摄氏度数是5℃,那么它的华氏度数是 ℉.
5.甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示.下列说法:①乙先到达青少年宫;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中正确的是 (填序号).
6.科学家研究发现声音在空气中传播的速度y(米/秒)与气温有的关系,若今天的气温是,则声音的传播速度是 米/秒.
二、单选题
7.据史书记载,漏刻是中国古代的一种计时工具,是古代人民对函数思想的创造性应用.研究发现水位 h(cm)与时间 t(min) 满足 h=0.4t+2,当 h 为 6cm时,时间 t 的值为( )
A.4.4min B.10min C.15min D.20min
8.在弹性限度内,弹簧挂上物体后会伸长,测得弹簧的长度与所挂物体的质量之间有如下关系:
0 1 2 3 4 5 …
10 10.5 11 11.5 12 12.5 …
在弹性限度内,所挂物体的质量为时,弹簧的长度为( )
A. B. C. D.
9.武汉市推出上网课包月制,每月收取上网课费用单位:元与上网时间单位:小时的函数关系如图所示若小明三月份在家上网课的费用为78元,则他三月份在家上网课的时间为( )
A.32小时 B.35小时 C.36小时 D.38小时
10.如图,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=BC=4,DE⊥BC于点E,且E是BC中点;动点P从点E出发沿路径ED→DA→AB以每秒1个单位长度的速度向终点B运动;设点P的运动时间为t秒,△PBC的面积为S,则下列能反映S与t的函数关系的图象是( )
A. B.
C. D.
11.如图, 甲乙两城市相距 千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市,已知货车出发 小时后客车再出发,先到终点的车辆原地休息,在汽车行驶过程中,设两车之间的距离为 (千米),客车出发的时间为 (小时),它们之间的关系如图所示,则下列结论:
①货车的速度是 千米/小时;②离开出发地后,两车第一次相遇时,距离出发地 千米;③货车从出发地到终点共用时 小时;④客车到达终点时,两车相距 千米.正确有( )
A. B. C. D.
三、解答题
12. 杆秤是我国传统的计重工具,其历史由来已久.如图1,可以用秤砣到秤纽的水平距离得出秤盘上所放物体的重量.称重时,若记秤砣到秤纽的水平距离为x(厘米),秤盘所放物体重量为y(斤),其部分对应数据如下表.
第1组 第2组 第3组 第4组 第5组 第6组
x(厘米) 1 3 4 6 11 12
y(斤)
(1)在图2中,通过描点的方法,判断哪一组数据是错误的
(2)据(1)的图象,选择合适的函数模型,并利用这种函数关系求当秤盘所放物体重量为5斤时秤砣到秤纽的水平距离.
四、计算题
13.1号探测气球从海拔5m出发,以1m/min的速度上升,与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升,两个气球都上升了1小时.
(1)用式子分别表示两个气球所在位置的海拔y(单位:m)关于上升时间t(单位:min)的函数关系;
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多少时间?位于什么高度?
五、综合题
14.“低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上下班.王叔叔某天骑自行车上班从家出发到单位过程中行进速度v(米/分钟)随时间t(分钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
(1)①当t=2分钟时,速度v= 米/分钟,路程s= 米;
②当t=15分钟时,速度v= 米/分钟,路程s= 米.
(2)当0≤t≤3和3<t≤15时,分别求出路程s(米)关于时间t(分钟)的函数解析式
(3)求王叔叔该天上班从家出发行进了750米时所用的时间t.
15.为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,2只A型节能灯和3只B型节能灯共需31元.
(1)求1只A型节能灯和1只B型节能灯的售价各是多少元?
(2)学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案,并说明理由.
16.随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 7 25 0.01
B m n 0.01
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
答案解析部分
1.【答案】(﹣4,0)
【知识点】一次函数的实际应用;一次函数的性质
2.【答案】
【知识点】一次函数的实际应用
3.【答案】-40
【知识点】一次函数的实际应用
4.【答案】41
【知识点】函数值;一次函数的实际应用
5.【答案】①②③
【知识点】一次函数的实际应用
6.【答案】342
【知识点】一次函数的实际应用
7.【答案】B
【知识点】一次函数的实际应用
8.【答案】C
【知识点】一次函数的实际应用
9.【答案】C
【知识点】一次函数的实际应用
10.【答案】B
【知识点】一次函数的实际应用
11.【答案】C
【知识点】一次函数的实际应用
12.【答案】(1)解:描点如图所示,
结合图形可知,除了第4组数据不同外,其他组数据均在图中的直线上,
故第4组数据是错误的;
(2)解:结合(1)上图可知,y(斤)与x(厘米)之间符合一次函数图象,
设y(斤)与x(厘米)之间的函数表达式为,
把,;,代入,
得,
解得:,
∴求y(斤)与x(厘米)之间的函数表达式为;
当时,,
解得:
∴当秤钩上所挂物重是5斤时,秤杆上秤砣到秤纽的水平距离是厘米;
【知识点】一次函数的实际应用;用表格表示变量间的关系;用图象表示变量间的关系
13.【答案】(1)解:根据题意得:1号探测气球所在位置的海拔:y1=t+5,2号探测气球所在位置的海拔:y2=0.5t+15;
(2)解:两个气球能位于同一高度,
根据题意得:t+5=0.5t+15,
解得:t=20,有t+5=25.
答:此时,气球上升了20分钟,都位于海拔25米的高度.
【知识点】一次函数的实际应用;列一次函数关系式
14.【答案】(1)200;200;300;4050
(2)解:①当0≤t≤3,设直线OA的解析式为:v=kt,由图象可知点A(3,300),
∴300=3k,
解得:k=100,
则解析式为:v=100t;
设l与OA的交点为P,则P(t,100t),
∴s=,
②当3<t≤15时,设l与AB的交点为Q,则Q(t,300),
∴S=
(3)解:∵当0≤t≤3,S最大=50×9=450,
∵750>450,
∴当3<t≤15时,450<S≤4050,
则令750=300t﹣450,
解得:t=4.
故王叔叔该天上班从家出发行进了750米时所用的时间4分钟.
【知识点】一次函数的实际应用
15.【答案】(1)解:设1只A型节能灯的售价是x元,1只B型节能灯的售价是y元,
,解得, ,
答:1只A型节能灯的售价是5元,1只B型节能灯的售价是7元
(2)解:设购买A型号的节能灯a只,则购买B型号的节能灯 只,费用为w元,
∴当 时,w取得最小值,此时
答:当购买A型号节能灯150只,B型号节能灯50只时最省钱
【知识点】一次函数的实际应用;二元一次方程组的实际应用-销售问题
16.【答案】(1)10;50
(2)解:yA与x之间的函数关系式为:
当x≤25时,yA=7,
当x>25时,yA=7+(x﹣25)×60×0.01,
∴yA=0.6x﹣8,
∴yA=;
(3)解:∵yB与x之间函数关系为:当x≤50时,yB=10,
当x>50时,yB=10+(x﹣50)×60×0.01=0.6x﹣20,
当0<x≤25时,yA=7,yB=50,
∴yA<yB,
∴选择A方式上网学习合算,
当25<x≤50时.yA=yB,即0.6x﹣8=10,解得;x=30,
∴当25<x<30时,yA<yB,选择A方式上网学习合算,
当x=30时,yA=yB,选择哪种方式上网学习都行,
当30<x≤50,yA>yB,选择B方式上网学习合算,
当x>50时,∵yA=0.6x﹣8,yB=0.6x﹣20,yA>yB,∴选择B方式上网学习合算,
综上所述:当0<x<30时,yA<yB,选择A方式上网学习合算,
当x=30时,yA=yB,选择哪种方式上网学习都行,
当x>30时,yA>yB,选择B方式上网学习合算.
【知识点】一次函数的实际应用
21世纪教育网(www.21cnjy.com)
2 / 9
