第19章 一次函数(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
第19章 一次函数
一、填空题
1.在函数 中,自变量x的取值范围 .
2.如图,一次函数与的图象交于点,则 .(填>,<)
3.函数y= 中,自变量x的取值范围是 .
4.如图,一次函数y=kx+b的图像经过A、B两点,那么关于x的不等式kx+b>0的解集是 .
5.直线 : 分别交 轴、 轴于 、 两点,直线 : 分别交 轴、 轴于 、 两点,在直线 上存在一点 ,能使得 ,则满足条件的点 的坐标为 .
6.如图,直线 与两坐标轴分别交于A、B两点,点C是 的中点,点D、E分别是直线 、y轴上的动点,则 的周长最小值是 .
二、单选题
7.直线 在 轴上的截距是( )
A.-3 B.2 C.3 D.
8.圆的周长公式是 ,那么在这个公式中,关于变量和常量的说法正确的是( )
A.2是常量,C、π、r是变量 B.2、π是常量,C、r是变量
C.2、C是常量,r、π是变量 D.2、π、r是常量,C是变量
9.一次函数y=-x+1的图象不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.一次函数y=﹣2x+3的图象上有两点A(1,y1),B(﹣2,y2),则y1与y2的大小关系是( )
A.y1<y2 B.y1≥y2 C.y1=y2 D.y1>y2
11.如图,一直线与坐标轴的正半轴分别交于A, B两点, P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为8,则该直线的函数表达式是( ).
A. B. C. D.
12.肥料的施用量与产量之间有一定的关系.研究表明,当每公顷钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:
氯肥施用量/kg 0 34 67 101 135 202 259 336 404 471
土豆产量/t 15.18 21.36 25.72 32.29 34.03 39.45 43.15 43.46 40.83 39.45
根据表格可知,下列说法正确的是( )
A.氮肥施用量越大,土豆产量越高
B.氮肥施用量是110kg时,土豆产量为34t
C.氯肥施用量是自变量,土豆产量是因变量
D.土豆产量为39.45t时,氮肥的施用量一定是202kg
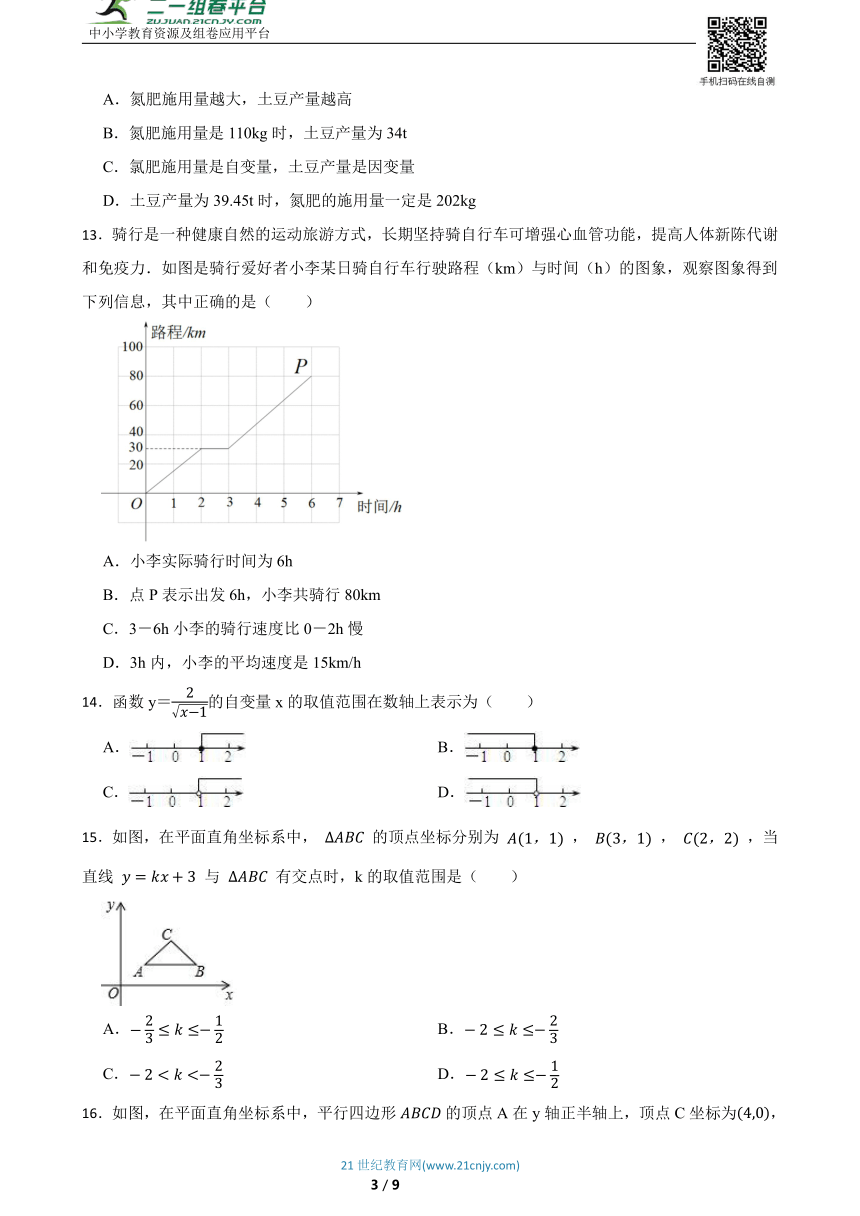
13.骑行是一种健康自然的运动旅游方式,长期坚持骑自行车可增强心血管功能,提高人体新陈代谢和免疫力.如图是骑行爱好者小李某日骑自行车行驶路程(km)与时间(h)的图象,观察图象得到下列信息,其中正确的是( )
A.小李实际骑行时间为6h
B.点P表示出发6h,小李共骑行80km
C.3-6h小李的骑行速度比0-2h慢
D.3h内,小李的平均速度是15km/h
14.函数y=的自变量x的取值范围在数轴上表示为( )
A. B.
C. D.
15.如图,在平面直角坐标系中, 的顶点坐标分别为 , , ,当直线 与 有交点时,k的取值范围是( )
A. B.
C. D.
16.如图,在平面直角坐标系中,平行四边形的顶点A在y轴正半轴上,顶点C坐标为,顶点D坐标为,对角线经过坐标原点O,边与x轴交于点E,对E点坐标为( )
A. B. C. D.
三、解答题
17.已知一次函数的图象过点,并且与y轴交于点P,直线与y轴交于点Q,点Q恰好与点P关于x轴对称,求这个一次函数的解析式.
18.已知一次函数的图象经过两点,求该一次函数的解析式.
19.一次函数 分别交x轴、y轴于点A、B,画图并求线段AB的长.
20.已知一次函数的图象经过点和点,求这个函数的解析式.
21.观察图,先填空,然后回答问题:
(1)由上而下第8行的白球与黑球总数比第5行多 个,若第n行白球与黑球的总数记作y,则y与n的关系式为
(2)第n行白球与黑球的总数可能是2023个吗?如果能,求出n的值;如果不能,说明理由.
22.直线与轴、轴分别交于点,无论取何值,直线经过定点.
(1)请直接写出定点的坐标;
(2)定义:在平面直角坐标系中,将点变换为(为常数),我们把这种变换称为“兔变换”,当时,点,经过“兔变换”后的对应点分别是,若轴,点在轴上,求;
(3)在(2)的条件下,点在轴上,连接,若,求点的坐标.
四、计算题
23.果实成熟从树上落到地面,它下落的高度与经过的时间有如下的关系:
时间t/秒 0.5 0.6 0.7 0.8 0.9 …
高度h/米 …
(1)上表反映了哪两个变量之间的关系?其中自变量是什么?因变量是什么?
(2)请你按照表中呈现的规律,列出果子下落的高度(米)与时间(秒)之间的关系式;
(3)现有一颗果子经过2秒后离地面一米,请计算这颗果子开始下落时离地面的高度是多少米?
24.(图1)中的摩天轮可抽象成一个圆,圆上一点离地面的高度与旋转时间 之间的关系如(图2)所示.
(1)根据(图2)填表:
0 3 6 8 …
…
(2)根据图中的信息,请写出摩天轮的直径.
25.如图,在平面直角坐标系中,函数的图象交x轴于点A、交y轴于点B,函数(m为常数)的图象为直线,交x轴于点C、交y轴于点D,直线与直线相交于点P.
(1)点A的坐标为__________,点B的坐标为_________.
(2)当时,求点P的坐标.
(3)当点P位于第四象限时,求m的取值范围.
(4)连结,,当的面积是面积的2倍时,直接写出m的值.
答案解析部分
1.【答案】x≥1且x≠2
【知识点】函数自变量的取值范围
2.【答案】>
【知识点】一次函数与不等式(组)的关系
3.【答案】x≤2且x≠﹣3
【知识点】函数自变量的取值范围
4.【答案】x>-3
【知识点】一次函数与不等式(组)的关系
5.【答案】 ,
【知识点】一次函数中的动态几何问题
6.【答案】
【知识点】勾股定理;轴对称的应用-最短距离问题;一次函数图象与坐标轴交点问题
7.【答案】A
【知识点】一次函数图象、性质与系数的关系
8.【答案】B
【知识点】常量、变量
9.【答案】C
【知识点】一次函数图象、性质与系数的关系
10.【答案】A
【知识点】一次函数的性质
11.【答案】C
【知识点】一次函数的实际应用
12.【答案】C
【知识点】函数的概念;函数的表示方法
13.【答案】B
【知识点】函数的图象
14.【答案】C
【知识点】函数自变量的取值范围
15.【答案】D
【知识点】一次函数图象、性质与系数的关系
16.【答案】B
【知识点】坐标与图形性质;待定系数法求一次函数解析式;平行四边形的性质;一次函数图象与坐标轴交点问题
17.【答案】y=﹣4x﹣3
【知识点】待定系数法求一次函数解析式;坐标与图形变化﹣对称;一次函数图象与坐标轴交点问题
18.【答案】
【知识点】待定系数法求一次函数解析式
19.【答案】解:因为当x=0时,y=2;当y=0时,x=1,
所以,与x轴的交点A(1,0),与y轴的交点B(0,2),
所以,线段AB的图象是
所以,AB=
【知识点】一次函数的图象;勾股定理
20.【答案】解:设函数解析式为,
一次函数的图象经过点和点,
,
解得,
所以,这个函数的解析式为.
【知识点】待定系数法求一次函数解析式
21.【答案】(1)9;
(2)解:不能;理由如下:
把代入,
得,
解得,,
∵n为正整数,
∴不存在哪一行白球与黑球的总数是2023个.
【知识点】函数值;用代数式表示图形变化规律
22.【答案】(1)定点的坐标为
(2)
(3)点的坐标为或
【知识点】坐标与图形性质;一次函数图象与坐标轴交点问题
23.【答案】(1)下落的角度h与经过的时间t之间的关系,自变量:经过的时间t,因变量:下落的高度h;(2);(3)这颗果子开始下落时离地面高度为20.6m.
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
24.【答案】(1)解:结合图象填表如下:
x(min) 0 3 6 8 …
y(m) 5 70 5 54 …
(2)解:∵最高点为70米,最低点为5米,
∴摩天轮的直径为65米.
【知识点】函数的图象
25.【答案】(1),
(2)点P的坐标为
(3)
(4)或
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;一次函数与二元一次方程(组)的关系;一次函数图象与坐标轴交点问题
21世纪教育网(www.21cnjy.com)
9 / 9
第19章 一次函数
一、填空题
1.在函数 中,自变量x的取值范围 .
2.如图,一次函数与的图象交于点,则 .(填>,<)
3.函数y= 中,自变量x的取值范围是 .
4.如图,一次函数y=kx+b的图像经过A、B两点,那么关于x的不等式kx+b>0的解集是 .
5.直线 : 分别交 轴、 轴于 、 两点,直线 : 分别交 轴、 轴于 、 两点,在直线 上存在一点 ,能使得 ,则满足条件的点 的坐标为 .
6.如图,直线 与两坐标轴分别交于A、B两点,点C是 的中点,点D、E分别是直线 、y轴上的动点,则 的周长最小值是 .
二、单选题
7.直线 在 轴上的截距是( )
A.-3 B.2 C.3 D.
8.圆的周长公式是 ,那么在这个公式中,关于变量和常量的说法正确的是( )
A.2是常量,C、π、r是变量 B.2、π是常量,C、r是变量
C.2、C是常量,r、π是变量 D.2、π、r是常量,C是变量
9.一次函数y=-x+1的图象不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.一次函数y=﹣2x+3的图象上有两点A(1,y1),B(﹣2,y2),则y1与y2的大小关系是( )
A.y1<y2 B.y1≥y2 C.y1=y2 D.y1>y2
11.如图,一直线与坐标轴的正半轴分别交于A, B两点, P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为8,则该直线的函数表达式是( ).
A. B. C. D.
12.肥料的施用量与产量之间有一定的关系.研究表明,当每公顷钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:
氯肥施用量/kg 0 34 67 101 135 202 259 336 404 471
土豆产量/t 15.18 21.36 25.72 32.29 34.03 39.45 43.15 43.46 40.83 39.45
根据表格可知,下列说法正确的是( )
A.氮肥施用量越大,土豆产量越高
B.氮肥施用量是110kg时,土豆产量为34t
C.氯肥施用量是自变量,土豆产量是因变量
D.土豆产量为39.45t时,氮肥的施用量一定是202kg
13.骑行是一种健康自然的运动旅游方式,长期坚持骑自行车可增强心血管功能,提高人体新陈代谢和免疫力.如图是骑行爱好者小李某日骑自行车行驶路程(km)与时间(h)的图象,观察图象得到下列信息,其中正确的是( )
A.小李实际骑行时间为6h
B.点P表示出发6h,小李共骑行80km
C.3-6h小李的骑行速度比0-2h慢
D.3h内,小李的平均速度是15km/h
14.函数y=的自变量x的取值范围在数轴上表示为( )
A. B.
C. D.
15.如图,在平面直角坐标系中, 的顶点坐标分别为 , , ,当直线 与 有交点时,k的取值范围是( )
A. B.
C. D.
16.如图,在平面直角坐标系中,平行四边形的顶点A在y轴正半轴上,顶点C坐标为,顶点D坐标为,对角线经过坐标原点O,边与x轴交于点E,对E点坐标为( )
A. B. C. D.
三、解答题
17.已知一次函数的图象过点,并且与y轴交于点P,直线与y轴交于点Q,点Q恰好与点P关于x轴对称,求这个一次函数的解析式.
18.已知一次函数的图象经过两点,求该一次函数的解析式.
19.一次函数 分别交x轴、y轴于点A、B,画图并求线段AB的长.
20.已知一次函数的图象经过点和点,求这个函数的解析式.
21.观察图,先填空,然后回答问题:
(1)由上而下第8行的白球与黑球总数比第5行多 个,若第n行白球与黑球的总数记作y,则y与n的关系式为
(2)第n行白球与黑球的总数可能是2023个吗?如果能,求出n的值;如果不能,说明理由.
22.直线与轴、轴分别交于点,无论取何值,直线经过定点.
(1)请直接写出定点的坐标;
(2)定义:在平面直角坐标系中,将点变换为(为常数),我们把这种变换称为“兔变换”,当时,点,经过“兔变换”后的对应点分别是,若轴,点在轴上,求;
(3)在(2)的条件下,点在轴上,连接,若,求点的坐标.
四、计算题
23.果实成熟从树上落到地面,它下落的高度与经过的时间有如下的关系:
时间t/秒 0.5 0.6 0.7 0.8 0.9 …
高度h/米 …
(1)上表反映了哪两个变量之间的关系?其中自变量是什么?因变量是什么?
(2)请你按照表中呈现的规律,列出果子下落的高度(米)与时间(秒)之间的关系式;
(3)现有一颗果子经过2秒后离地面一米,请计算这颗果子开始下落时离地面的高度是多少米?
24.(图1)中的摩天轮可抽象成一个圆,圆上一点离地面的高度与旋转时间 之间的关系如(图2)所示.
(1)根据(图2)填表:
0 3 6 8 …
…
(2)根据图中的信息,请写出摩天轮的直径.
25.如图,在平面直角坐标系中,函数的图象交x轴于点A、交y轴于点B,函数(m为常数)的图象为直线,交x轴于点C、交y轴于点D,直线与直线相交于点P.
(1)点A的坐标为__________,点B的坐标为_________.
(2)当时,求点P的坐标.
(3)当点P位于第四象限时,求m的取值范围.
(4)连结,,当的面积是面积的2倍时,直接写出m的值.
答案解析部分
1.【答案】x≥1且x≠2
【知识点】函数自变量的取值范围
2.【答案】>
【知识点】一次函数与不等式(组)的关系
3.【答案】x≤2且x≠﹣3
【知识点】函数自变量的取值范围
4.【答案】x>-3
【知识点】一次函数与不等式(组)的关系
5.【答案】 ,
【知识点】一次函数中的动态几何问题
6.【答案】
【知识点】勾股定理;轴对称的应用-最短距离问题;一次函数图象与坐标轴交点问题
7.【答案】A
【知识点】一次函数图象、性质与系数的关系
8.【答案】B
【知识点】常量、变量
9.【答案】C
【知识点】一次函数图象、性质与系数的关系
10.【答案】A
【知识点】一次函数的性质
11.【答案】C
【知识点】一次函数的实际应用
12.【答案】C
【知识点】函数的概念;函数的表示方法
13.【答案】B
【知识点】函数的图象
14.【答案】C
【知识点】函数自变量的取值范围
15.【答案】D
【知识点】一次函数图象、性质与系数的关系
16.【答案】B
【知识点】坐标与图形性质;待定系数法求一次函数解析式;平行四边形的性质;一次函数图象与坐标轴交点问题
17.【答案】y=﹣4x﹣3
【知识点】待定系数法求一次函数解析式;坐标与图形变化﹣对称;一次函数图象与坐标轴交点问题
18.【答案】
【知识点】待定系数法求一次函数解析式
19.【答案】解:因为当x=0时,y=2;当y=0时,x=1,
所以,与x轴的交点A(1,0),与y轴的交点B(0,2),
所以,线段AB的图象是
所以,AB=
【知识点】一次函数的图象;勾股定理
20.【答案】解:设函数解析式为,
一次函数的图象经过点和点,
,
解得,
所以,这个函数的解析式为.
【知识点】待定系数法求一次函数解析式
21.【答案】(1)9;
(2)解:不能;理由如下:
把代入,
得,
解得,,
∵n为正整数,
∴不存在哪一行白球与黑球的总数是2023个.
【知识点】函数值;用代数式表示图形变化规律
22.【答案】(1)定点的坐标为
(2)
(3)点的坐标为或
【知识点】坐标与图形性质;一次函数图象与坐标轴交点问题
23.【答案】(1)下落的角度h与经过的时间t之间的关系,自变量:经过的时间t,因变量:下落的高度h;(2);(3)这颗果子开始下落时离地面高度为20.6m.
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
24.【答案】(1)解:结合图象填表如下:
x(min) 0 3 6 8 …
y(m) 5 70 5 54 …
(2)解:∵最高点为70米,最低点为5米,
∴摩天轮的直径为65米.
【知识点】函数的图象
25.【答案】(1),
(2)点P的坐标为
(3)
(4)或
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;一次函数与二元一次方程(组)的关系;一次函数图象与坐标轴交点问题
21世纪教育网(www.21cnjy.com)
9 / 9
