20.1.2中位数和众数(含答案)
文档属性
| 名称 | 20.1.2中位数和众数(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1001.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-21 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
20.1.2中位数和众数
一、填空题
1.根据某班40名同学一周的体育锻炼情况绘制了如下统计表,那么关于该班40名同学一周的体育锻炼时间的中位数是 小时.
时间(小时) 7 8 9 10
人数(人) 3 17 14 6
2.某班全体学生参加了一次“献爱心一日捐”活动,捐款人数与捐款额如图所示,根据图中所提供的信息,你认为这次捐款活动中捐款额的中位数是 元.
3.某校7名初中男生参加引体向上体育测试的成绩分别为:8,5,7,5,8,6,8,则这组数据的众数和中位数分别为 .
4.邗江区青少年活动中心组织一次少年跳绳比赛,各年龄组的参赛人数如下表所示:
年龄组 12岁 13岁 14岁 15岁
参赛人数 5 20 12 13
则全体参赛选手年龄的中位数是 岁.
5.在2014年重庆市初中毕业生体能测试中,某校初三有7名同学的体能测试成绩(单位:分)如下:50,48,47,50,48,49,48.这组数据的众数是 .
6.已知一组数据5,4,x,3,9众数为3,则这组数据的中位数是 .
二、单选题
7.铜桐收藏有枚南宋铁钱“庆元通宝”(如图所示),测得它们的质量(单位:)分别为、、、、、、.这组数据的中位数为( )
A. B. C. D.
8.若在一组数据2,2,3,4,4中添加一个数后,它们的平均数不变,则添加数据后这组数据的中位数是( )
A.3 B.4 C.3.5 D.4.5
9.某校在“中国梦 我的梦”演讲比赛中,有15名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前8名,不仅要了解自己的成绩,还要了解这15名学生成绩的( )
A.平均数 B.众数 C.中位数 D.方差
10.一名射击爱好者5次射击的中靶环数如下:6,7,9,8,9.这5个数据的众数是( )
A.6 B.7 C.8 D.9
11.某篮球兴趣小组名学生参加投篮比赛,每人投个,投中的个数分别为:,,,,,,,则这组数据的众数和中位数分别为( )
A., B., C., D.,
三、解答题
12.为了落实“双减”政策.某校进行了课时作业分层设计课题研究,分别在A,B,C三个班开展比对实验.A班没有开展分层作业设计,B班开展“好、差”两层分层设计,C班开展“好、中、差”三层分层及个别学生特殊布置设计.一段时间后对实验前、后开展的前测和后测(难度、题型、总分相同的试卷,满分100分)数据进行整理比对,如表1和表2.
表1:前测数据
测试分数
A班(常态班) 28 9 9 3 1
B班(实验班) 25 10 8 2 1
C班(实验班) 26 9 8 1 2
表2:后测数据
测试分数
A班(常态班) 14 16 12 6 2
B班(实验班) 6 8 11 18 3
C班(实验班) 4 6 9 22 5
(1)请选择一种适当的统计量,分别比较A,B,C三个班的后测数据
(2)通过分析前测、后测数据,请对该校开展的课时作业分层设计实验效果进行评价.
四、计算题
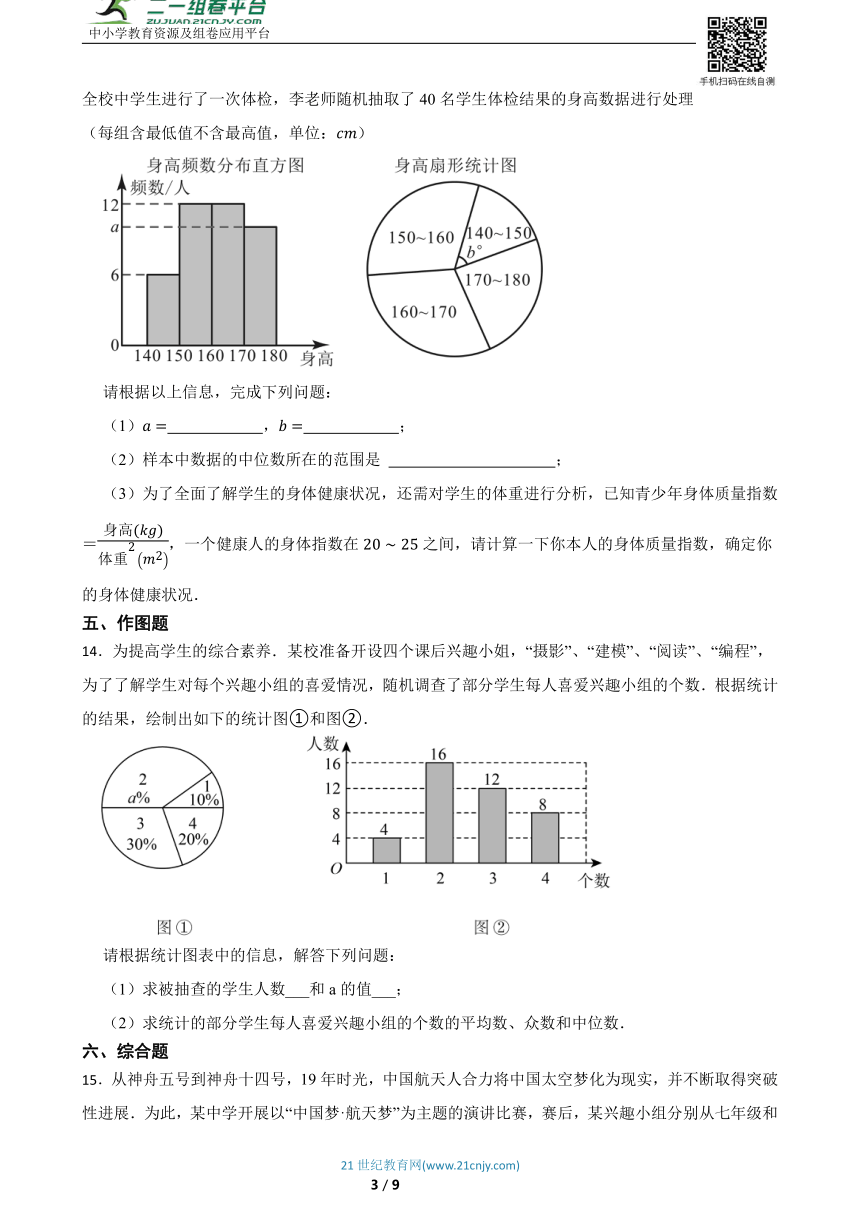
13.随着经济水平的提升,人们越来越重视体育健康,为了解中学生身体素质指标合格情况,某校对全校中学生进行了一次体检,李老师随机抽取了40名学生体检结果的身高数据进行处理(每组含最低值不含最高值,单位:)
请根据以上信息,完成下列问题:
(1) , ;
(2)样本中数据的中位数所在的范围是 ;
(3)为了全面了解学生的身体健康状况,还需对学生的体重进行分析,已知青少年身体质量指数=,一个健康人的身体指数在之间,请计算一下你本人的身体质量指数,确定你的身体健康状况.
五、作图题
14.为提高学生的综合素养.某校准备开设四个课后兴趣小姐,“摄影”、“建模”、“阅读”、“编程”,为了了解学生对每个兴趣小组的喜爱情况,随机调查了部分学生每人喜爱兴趣小组的个数.根据统计的结果,绘制出如下的统计图①和图②.
请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数___和a的值___;
(2)求统计的部分学生每人喜爱兴趣小组的个数的平均数、众数和中位数.
六、综合题
15.从神舟五号到神舟十四号,19年时光,中国航天人合力将中国太空梦化为现实,并不断取得突破性进展.为此,某中学开展以“中国梦·航天梦”为主题的演讲比赛,赛后,某兴趣小组分别从七年级和八年级参赛选手中各随机抽取5名同学,将他们的比赛成绩统计如图:
根据图中信息,解答下列问题:
(1)七年级5名被抽取的选手中,比赛成绩的中位数为____________分;
(2)八年级5名被抽取的选手中,比赛成绩的众数为______________分;
(3)分别计算两个年级被抽取的选手的平均成绩,并估计哪个年级的平均成绩较高?
16.中华鲟是国家一级保护动物,它是大型洄游性鱼类,生在长江,长在海洋,受生态环境的影响,数量逐年下降。中华鲟研究所每年定期通过人工养殖放流来增加中华鲟的数量,每年放流的中华鲟中有少数体内安装了长效声呐标记,便于检测它们从长江到海洋的适应情况,这部分中华鲟简称为“声呐鲟”,研究所收集了它们到达下游监测点A的时间t(h)的相关数据,并制作如下不完整统计图和统计表.
已知:今年和去年分别有20尾“声呐鲟”在放流的96小时内到达监测点A,今年落在24今年20尾“声呐鲟”到达监测点A所用时间t(h)的频数分布直方图
关于“声呐鲟”到达监测点A所用时间t(h)的统计表
平均数 中位数 众数 方差
去年 64.2 68 73 715.6
今年 56.2 a 68 629.7
(1)请补全频数分布直方图,并根据以上信息填空:a= ;
(2)中华鲟到达海洋的时间越快,说明它从长江到海洋的适应情况就越好,请根据上述信息,选择一个统计量说明去年和今年中哪一年中华鲟从长江到海洋的适应情况更好;
(3)去年和今年该放流点共放流1300尾中华鲟,其中“声呐鲟”共有50尾,请估计今年和去年在放流72小时内共有多少尾中华鲟通过监测站A.
17.停课不停学,疫情期间,八(1)班30位同学参加运动线上打卡,张老师为了鼓励同学们积极锻炼,统计了这30人15天的打卡次数如表:
打卡次数 7 8 9 14 15
人数 6 9 6 3 6
(1)直接写出打卡次数的众数和中位数;
(2)求所有同学打卡次数的平均数;
(3)为了调动同学们锻炼的积极性,张老师决定制定一个打卡奖励标准,凡打卡次数达到或超过这个标准的同学将获得奖励.请你根据(1)、(2)中所求的统计量,帮助张老师制定一个较为合理的打卡奖励标准,并说明理由.
七、实践探究题
18. “防溺水”是校园安全教育工作重点之一.某校为确保学生安全,开展了“远离溺水 珍爱生命”的防溺水安全知识竞赛.现从七年级、八年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
七年级:92,75,82,96,84,90,85,97,85,92,68,100,85,86,95,85,89,90,91,93.
八年级:90,87,93,97,90,84,92,72,100,80,90,91,59,93,87,90,82,91,92,100.
【整理与分析数据】
50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100
七年级 0 1 1 8 a
八年级 1 0 1 5 13
【应用数据】
平均数 众数 中位数
七年级 88 85 b
八年级 88 c 90
(1)由上表填空:a= ,b= ,c= ;
(2)若成绩不低于90分为优秀等次,该校七、八年级共有学生1600人,请你估计两个年级在本次竞赛中获得优秀等次的共有多少人?
(3)你认为哪个年级的学生对防溺水安全知识掌握的总体水平较好,请从两个不同的角度说明理由.
答案解析部分
1.【答案】8.5
【知识点】中位数
2.【答案】15
【知识点】中位数
3.【答案】8,7
【知识点】中位数;众数
4.【答案】13.5
【知识点】中位数
5.【答案】48
【知识点】众数
6.【答案】4
【知识点】中位数;众数
7.【答案】B
【知识点】中位数
8.【答案】A
【知识点】平均数及其计算;中位数
9.【答案】C
【知识点】常用统计量的选择
10.【答案】D
【知识点】众数
11.【答案】A
【知识点】中位数;众数
12.【答案】(1)从中位数看,C班成绩最好,其次是B班,再是A班(答案不唯一)
(2)从中位数看,作业分层越精细,成绩越好,故该校开展的课时作业分层设计实验效果显著(答案不唯一).
【知识点】统计表;中位数
13.【答案】(1)10;54
(2)
(3)21.5(答案不唯一)
【知识点】频数(率)分布直方图;扇形统计图;中位数
14.【答案】(1)40,40;
(2)平均数是,众数是2,中位数为
【知识点】加权平均数及其计算;中位数;众数
15.【答案】(1)90
(2)80
(3)七年级的平均成绩为86分,八年级的平均成绩为84分,估计七年级的平均成绩更高
【知识点】平均数及其计算;中位数;众数
16.【答案】(1)64
(2)解:选择平均数,
由表可知,去年“声呐鲟”到达下游监测点的平均时间为64.2小时,而今年“声呐鲟”到达下游监测点的平均时间为56.2小时,缩短了8小时,
所以今年“声呐鲟”从长江到海洋的适应情况更好(答案不唯一,合理即可).
(3)解:1300×(尾).
答:其中“声呐鲟”共有50尾,请估计今年和去年在放流72小时内共有624尾中华鲟通过监测站A.
【知识点】用样本估计总体;频数(率)分布直方图;扇形统计图;分析数据的集中趋势(平均数、中位数、众数)
17.【答案】(1)解:8次的人数最多,众数为8次;
共30人,所有同学打卡次数从小到大排列第15个、第16个数反比为8次,9次,
中位数为(8+9)÷2=8.5(次);
(2)解:平均数为(7×6+8×9+9×6+14×3+15×6)÷30=10(次);
(3)解:为了调动同学们锻炼的积极性,打卡奖励标准可以定为所有同学打卡次数的中位数.
因为共有30人,9次以上(含9次)的有17人,超过总数的一半.
【知识点】加权平均数及其计算;中位数;常用统计量的选择;众数
18.【答案】(1)10;;90
(2)解:(人),
答:估计两个年级在本次竞赛中获得优秀等次的共有920人.
(3)解:八年级的学生对防溺水安全知识掌握的总体水平较好.
理由:七、八年级的平均分相等;八年级成绩的众数为90,高于七年级学生成绩的众数85;八年级成绩的中位数为90,高于七年级学生成绩的中位数,综合比较,八年级的学生对防溺水安全知识掌握的总体水平较好.
【知识点】频数(率)分布表;中位数;分析数据的集中趋势(平均数、中位数、众数);众数
21世纪教育网(www.21cnjy.com)
2 / 9
20.1.2中位数和众数
一、填空题
1.根据某班40名同学一周的体育锻炼情况绘制了如下统计表,那么关于该班40名同学一周的体育锻炼时间的中位数是 小时.
时间(小时) 7 8 9 10
人数(人) 3 17 14 6
2.某班全体学生参加了一次“献爱心一日捐”活动,捐款人数与捐款额如图所示,根据图中所提供的信息,你认为这次捐款活动中捐款额的中位数是 元.
3.某校7名初中男生参加引体向上体育测试的成绩分别为:8,5,7,5,8,6,8,则这组数据的众数和中位数分别为 .
4.邗江区青少年活动中心组织一次少年跳绳比赛,各年龄组的参赛人数如下表所示:
年龄组 12岁 13岁 14岁 15岁
参赛人数 5 20 12 13
则全体参赛选手年龄的中位数是 岁.
5.在2014年重庆市初中毕业生体能测试中,某校初三有7名同学的体能测试成绩(单位:分)如下:50,48,47,50,48,49,48.这组数据的众数是 .
6.已知一组数据5,4,x,3,9众数为3,则这组数据的中位数是 .
二、单选题
7.铜桐收藏有枚南宋铁钱“庆元通宝”(如图所示),测得它们的质量(单位:)分别为、、、、、、.这组数据的中位数为( )
A. B. C. D.
8.若在一组数据2,2,3,4,4中添加一个数后,它们的平均数不变,则添加数据后这组数据的中位数是( )
A.3 B.4 C.3.5 D.4.5
9.某校在“中国梦 我的梦”演讲比赛中,有15名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前8名,不仅要了解自己的成绩,还要了解这15名学生成绩的( )
A.平均数 B.众数 C.中位数 D.方差
10.一名射击爱好者5次射击的中靶环数如下:6,7,9,8,9.这5个数据的众数是( )
A.6 B.7 C.8 D.9
11.某篮球兴趣小组名学生参加投篮比赛,每人投个,投中的个数分别为:,,,,,,,则这组数据的众数和中位数分别为( )
A., B., C., D.,
三、解答题
12.为了落实“双减”政策.某校进行了课时作业分层设计课题研究,分别在A,B,C三个班开展比对实验.A班没有开展分层作业设计,B班开展“好、差”两层分层设计,C班开展“好、中、差”三层分层及个别学生特殊布置设计.一段时间后对实验前、后开展的前测和后测(难度、题型、总分相同的试卷,满分100分)数据进行整理比对,如表1和表2.
表1:前测数据
测试分数
A班(常态班) 28 9 9 3 1
B班(实验班) 25 10 8 2 1
C班(实验班) 26 9 8 1 2
表2:后测数据
测试分数
A班(常态班) 14 16 12 6 2
B班(实验班) 6 8 11 18 3
C班(实验班) 4 6 9 22 5
(1)请选择一种适当的统计量,分别比较A,B,C三个班的后测数据
(2)通过分析前测、后测数据,请对该校开展的课时作业分层设计实验效果进行评价.
四、计算题
13.随着经济水平的提升,人们越来越重视体育健康,为了解中学生身体素质指标合格情况,某校对全校中学生进行了一次体检,李老师随机抽取了40名学生体检结果的身高数据进行处理(每组含最低值不含最高值,单位:)
请根据以上信息,完成下列问题:
(1) , ;
(2)样本中数据的中位数所在的范围是 ;
(3)为了全面了解学生的身体健康状况,还需对学生的体重进行分析,已知青少年身体质量指数=,一个健康人的身体指数在之间,请计算一下你本人的身体质量指数,确定你的身体健康状况.
五、作图题
14.为提高学生的综合素养.某校准备开设四个课后兴趣小姐,“摄影”、“建模”、“阅读”、“编程”,为了了解学生对每个兴趣小组的喜爱情况,随机调查了部分学生每人喜爱兴趣小组的个数.根据统计的结果,绘制出如下的统计图①和图②.
请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数___和a的值___;
(2)求统计的部分学生每人喜爱兴趣小组的个数的平均数、众数和中位数.
六、综合题
15.从神舟五号到神舟十四号,19年时光,中国航天人合力将中国太空梦化为现实,并不断取得突破性进展.为此,某中学开展以“中国梦·航天梦”为主题的演讲比赛,赛后,某兴趣小组分别从七年级和八年级参赛选手中各随机抽取5名同学,将他们的比赛成绩统计如图:
根据图中信息,解答下列问题:
(1)七年级5名被抽取的选手中,比赛成绩的中位数为____________分;
(2)八年级5名被抽取的选手中,比赛成绩的众数为______________分;
(3)分别计算两个年级被抽取的选手的平均成绩,并估计哪个年级的平均成绩较高?
16.中华鲟是国家一级保护动物,它是大型洄游性鱼类,生在长江,长在海洋,受生态环境的影响,数量逐年下降。中华鲟研究所每年定期通过人工养殖放流来增加中华鲟的数量,每年放流的中华鲟中有少数体内安装了长效声呐标记,便于检测它们从长江到海洋的适应情况,这部分中华鲟简称为“声呐鲟”,研究所收集了它们到达下游监测点A的时间t(h)的相关数据,并制作如下不完整统计图和统计表.
已知:今年和去年分别有20尾“声呐鲟”在放流的96小时内到达监测点A,今年落在24
关于“声呐鲟”到达监测点A所用时间t(h)的统计表
平均数 中位数 众数 方差
去年 64.2 68 73 715.6
今年 56.2 a 68 629.7
(1)请补全频数分布直方图,并根据以上信息填空:a= ;
(2)中华鲟到达海洋的时间越快,说明它从长江到海洋的适应情况就越好,请根据上述信息,选择一个统计量说明去年和今年中哪一年中华鲟从长江到海洋的适应情况更好;
(3)去年和今年该放流点共放流1300尾中华鲟,其中“声呐鲟”共有50尾,请估计今年和去年在放流72小时内共有多少尾中华鲟通过监测站A.
17.停课不停学,疫情期间,八(1)班30位同学参加运动线上打卡,张老师为了鼓励同学们积极锻炼,统计了这30人15天的打卡次数如表:
打卡次数 7 8 9 14 15
人数 6 9 6 3 6
(1)直接写出打卡次数的众数和中位数;
(2)求所有同学打卡次数的平均数;
(3)为了调动同学们锻炼的积极性,张老师决定制定一个打卡奖励标准,凡打卡次数达到或超过这个标准的同学将获得奖励.请你根据(1)、(2)中所求的统计量,帮助张老师制定一个较为合理的打卡奖励标准,并说明理由.
七、实践探究题
18. “防溺水”是校园安全教育工作重点之一.某校为确保学生安全,开展了“远离溺水 珍爱生命”的防溺水安全知识竞赛.现从七年级、八年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
七年级:92,75,82,96,84,90,85,97,85,92,68,100,85,86,95,85,89,90,91,93.
八年级:90,87,93,97,90,84,92,72,100,80,90,91,59,93,87,90,82,91,92,100.
【整理与分析数据】
50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100
七年级 0 1 1 8 a
八年级 1 0 1 5 13
【应用数据】
平均数 众数 中位数
七年级 88 85 b
八年级 88 c 90
(1)由上表填空:a= ,b= ,c= ;
(2)若成绩不低于90分为优秀等次,该校七、八年级共有学生1600人,请你估计两个年级在本次竞赛中获得优秀等次的共有多少人?
(3)你认为哪个年级的学生对防溺水安全知识掌握的总体水平较好,请从两个不同的角度说明理由.
答案解析部分
1.【答案】8.5
【知识点】中位数
2.【答案】15
【知识点】中位数
3.【答案】8,7
【知识点】中位数;众数
4.【答案】13.5
【知识点】中位数
5.【答案】48
【知识点】众数
6.【答案】4
【知识点】中位数;众数
7.【答案】B
【知识点】中位数
8.【答案】A
【知识点】平均数及其计算;中位数
9.【答案】C
【知识点】常用统计量的选择
10.【答案】D
【知识点】众数
11.【答案】A
【知识点】中位数;众数
12.【答案】(1)从中位数看,C班成绩最好,其次是B班,再是A班(答案不唯一)
(2)从中位数看,作业分层越精细,成绩越好,故该校开展的课时作业分层设计实验效果显著(答案不唯一).
【知识点】统计表;中位数
13.【答案】(1)10;54
(2)
(3)21.5(答案不唯一)
【知识点】频数(率)分布直方图;扇形统计图;中位数
14.【答案】(1)40,40;
(2)平均数是,众数是2,中位数为
【知识点】加权平均数及其计算;中位数;众数
15.【答案】(1)90
(2)80
(3)七年级的平均成绩为86分,八年级的平均成绩为84分,估计七年级的平均成绩更高
【知识点】平均数及其计算;中位数;众数
16.【答案】(1)64
(2)解:选择平均数,
由表可知,去年“声呐鲟”到达下游监测点的平均时间为64.2小时,而今年“声呐鲟”到达下游监测点的平均时间为56.2小时,缩短了8小时,
所以今年“声呐鲟”从长江到海洋的适应情况更好(答案不唯一,合理即可).
(3)解:1300×(尾).
答:其中“声呐鲟”共有50尾,请估计今年和去年在放流72小时内共有624尾中华鲟通过监测站A.
【知识点】用样本估计总体;频数(率)分布直方图;扇形统计图;分析数据的集中趋势(平均数、中位数、众数)
17.【答案】(1)解:8次的人数最多,众数为8次;
共30人,所有同学打卡次数从小到大排列第15个、第16个数反比为8次,9次,
中位数为(8+9)÷2=8.5(次);
(2)解:平均数为(7×6+8×9+9×6+14×3+15×6)÷30=10(次);
(3)解:为了调动同学们锻炼的积极性,打卡奖励标准可以定为所有同学打卡次数的中位数.
因为共有30人,9次以上(含9次)的有17人,超过总数的一半.
【知识点】加权平均数及其计算;中位数;常用统计量的选择;众数
18.【答案】(1)10;;90
(2)解:(人),
答:估计两个年级在本次竞赛中获得优秀等次的共有920人.
(3)解:八年级的学生对防溺水安全知识掌握的总体水平较好.
理由:七、八年级的平均分相等;八年级成绩的众数为90,高于七年级学生成绩的众数85;八年级成绩的中位数为90,高于七年级学生成绩的中位数,综合比较,八年级的学生对防溺水安全知识掌握的总体水平较好.
【知识点】频数(率)分布表;中位数;分析数据的集中趋势(平均数、中位数、众数);众数
21世纪教育网(www.21cnjy.com)
2 / 9
