2024-2025学年上海南洋模范中学高三上学期数学月考试卷及答案(2024.11)(含答案)
文档属性
| 名称 | 2024-2025学年上海南洋模范中学高三上学期数学月考试卷及答案(2024.11)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 918.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-21 21:28:38 | ||
图片预览




文档简介
南模中学2024学年第一学期高三年级数学月考
2024.11
一、填空题(本大题共12题,满分54分,第1-6题每题4分,第7-12题每题5分)
1.若集合,则________.
2.已知向量,,若,则________.
3.若一元二次不等式的解集是,则的值是________.
4.直线与圆相交,所得的弦的长为________.
5.设事件,是互斥事件,且,则________.
6.设,,若,则的最大值为________.
7.从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有________种,(用数字填写答案)
8.设,若
,则________.
9.容量为的一组数据,它的第百分位数(为1到99之间的整数)各不相同,则的最小值为________.
10.若函数在区间上有最大值,则实数的取值范围是________.
11.已知,且是复数,当的最大值为3,则________.
12.已知平面向量,,满足与的夹角为锐角,,,,且的最小值为,向量的取值范围是________.
二、选择题(本大题共4题,满分18分,第13-14题每题4分,第15-16题每题5分)
13.已知是偶函数,则( )
A. B. C.1 D.2
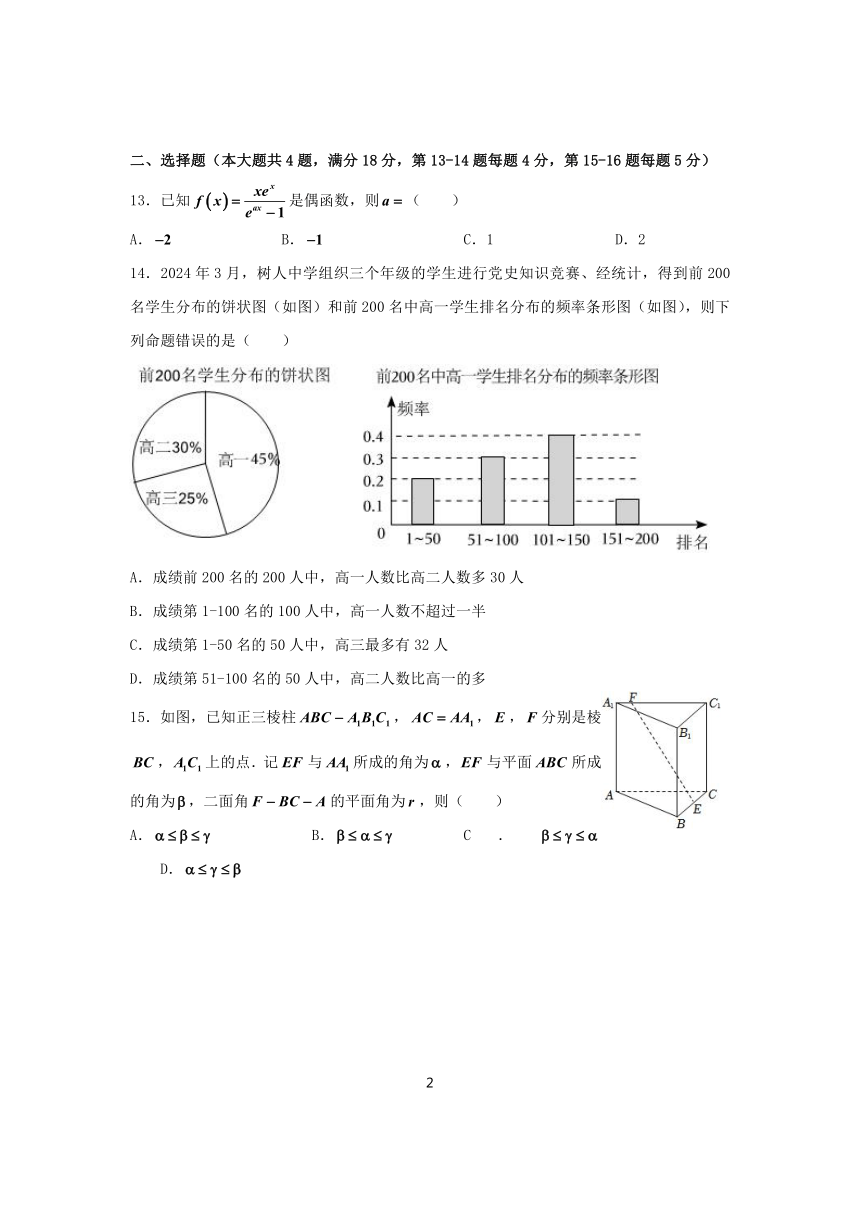
14.2024年3月,树人中学组织三个年级的学生进行党史知识竞赛、经统计,得到前200名学生分布的饼状图(如图)和前200名中高一学生排名分布的频率条形图(如图),则下列命题错误的是( )
A.成绩前200名的200人中,高一人数比高二人数多30人
B.成绩第1-100名的100人中,高一人数不超过一半
C.成绩第1-50名的50人中,高三最多有32人
D.成绩第51-100名的50人中,高二人数比高一的多
15.如图,已知正三棱柱,,,分别是棱,上的点.记与所成的角为,与平面所成的角为,二面角的平面角为,则( )
A. B. C. D.
16.已知数列满足(为正整数),,设集合.有以下两个猜想:①不论取何值,总有;②若,且数列中恰好存在连续的7项构成等比数列,则的可能取值有6个.其中( ).
A.①正确,②正确 B.①正确,②错误
C.①错误,②正确 D.①错误,②错误
三、解答题
17.如图所示的几何体是圆锥的一半和一个三棱锥组成,圆锥底面圆的半径为1,圆锥的高,三棱锥的底面是以圆锥的底面圆的直径为斜边的等腰直角三角形,且与圆锥底面在同一个平面上.
(1)求直线和平面所成角的大小;
(2)求该几何体的体积.
18.在三角形中,内角,,所对边分别为,,,已知.
(I)求角的大小;
(2)若,三角形的面积为,求三角形的周长.
19.汽车智能辅助驾驶已得到广泛应用,其自动刹车的工作原理是用雷达测出车辆与前方障碍物之间的距离(并结合车速转化为所需时间),当此距离等于报警距离时就开始报警提醒,等于危险距离时就自动刹车、某种算法(如下图所示)将报警时间划分为4段,分别为准备时间、人的反应时间、系统反应时间、制动时间,相应的距离分别为、、、.当车速为(米/秒),且时,通过大数据统计分析得到下表(其中系数随地面湿滑程度等路面情况而变化,)
阶段 0、准备 1、人的反应 2、系统反应 3、制动
时间 秒 秒
距离 米 米
(I)请写出报警距离(米)与车速(米/秒)之间的函数关系式,并求时,若汽车达到报警距离时人和系统均不采取任何制动措施,仍以此速度行驶,则汽车撞上固定障碍物的最短时间。(精确到0.1秒)
(2)若要求汽车不论在何种路面情况下行驶,报警距离均小于80米,则汽车的行驶速度应限制在多少米/秒以下?合多少千米/小时(精确到1千米/小时)?
20.如图所示,由椭圆和椭圆组合而成的曲线,由图形特点,这里称曲线为“猫眼曲线”,特别地,若两个椭圆的离心率相等,则称其为“优美猫眼曲线”.
(1)已知猫眼曲线满足,,成等比数列,试判断该曲线是否为“优美猫眼曲线”;
(2)在曲线中,若,,,斜率为的直线不经过坐标原点,且与椭圆相交所得弦的中点为,与椭圆相交所得弦的中点为,证明:直线,的斜率之比为定值;
(3)在(2)的条件下,若直线的斜率,且与椭圆相切,与椭圆相交于,两点,为椭圆上异于,的任意一点,求面积的最大值.
21.对于函数的导函数,若在其定义域内存在实数和,使得成立,称是“青峰”函数,并称是的“青峰值”.
(1)试分别判断函数,和,是不是“青峰”函数?并说明理由;
(2)若是“青峰”函数,且“青峰值”为2,求实数的取值范围;
(3)证明:是“青峰”函数,并求出该函数“青峰值”的取值范围.
参考答案
一、填空题
1.; 2.; 3.; 4.; 5.; 6.; 7.; 8.; 9.; 10.; 11.; 12.;
11.已知,且是复数,当的最大值为3,则________.
【答案】
【解析】设是实数,则,,
综上,勺最大值为,即有.故答案为:.
12.已知平面向量,,满足与的夹角为锐角,,,,且的最小值为,向量的取值范围是________.
【答案】
【解析】设与的夹角为,则,
当,上式有最小值为,的最小值为
的最小值为3,,解得.
又,此时,,
与的夹角为,且
不妨设,
向量的取值范围是故答案为:
二、选择题
13.C; 14.D; 15.A; 16.A
15.如图,已知正三棱柱,,,分别是棱,上的点.记与所成的角为,与平面所成的角为,二面角的平面角为,则( )
A. B. C. D.
【答案】
【解析】正三棱柱中,正三棱柱的所有棱长相等,设棱长为1,如图,过作,垂足点为,连接,则,
与所成的角为,且,
又,与平面所成的角为,
且①
再过点作,垂足点为,连接,又易知底面底面,
,又平面
二面角的平面角为,且,
②,又,③
由①②③得,又在单调递增,
故选:.
16.已知数列满足(为正整数),,设集合.有以下两个猜想:①不论取何值,总有;②若,且数列中恰好存在连续的7项构成等比数列,则的可能取值有6个.其中( ).
A.①正确,②正确 B.①正确,②错误
C.①错误,②正确 D.①错误,②错误
【答案】
【解析】不妨设出数列中的一项,
①若被3除余1,则由已知可得,,
若被3除余2,则由已知可得,,
若被3除余0,则由已知可得,,
所以对对任意的,则,
所以对数列中的任一项,若,则,因为,所以,
所以数列中必存在某一项(否则与上述结论矛盾),若,结论得证,
若,则,,结论得证,若,则,得证,
所以,不论取何值,总有;故①正确;
②若是3的倍数,则,
若被3除余1,则由已知可得,,
若被3除余2,则由已知可得,,
所以连续的7项构成等比数列的公比为,
因为,所以这7项中前6项一定都量3的倍数,
而第七项一定不是3的倍数(否则构成等比数列的连接项数会多于7项),
设第7项为,则是被3除余1或余2的正整数,则可推得,
因为,所以,或,
由递推关系式可知,在该数列的前项中,满足小于等于2022的项只有;,或,或,
所以首项的有可能取值的集合为,,
故的可能取值有6个.故②正确.故选:.
三、解答题
17.(1) (2)
18.(1) (2)
19.(1);3.1秒 (2)20米/秒;72千米/小时
20.如图所示,由椭圆和椭圆组合而成的曲线,由图形特点,这里称曲线为“猫眼曲线”,特别地,若两个椭圆的离心率相等,则称其为“优美猫眼曲线”.
(1)已知猫眼曲线满足,,成等比数列,试判断该曲线是否为“优美猫眼曲线”;
(2)在曲线中,若,,,斜率为的直线不经过坐标原点,且与椭圆相交所得弦的中点为,与椭圆相交所得弦的中点为,证明:直线,的斜率之比为定值;
(3)在(2)的条件下,若直线的斜率,且与椭圆相切,与椭圆相交于,两点,为椭圆上异于,的任意一点,求面积的最大值.
【答案】(1)见解析 (2)见解析 (3)
【解析】(1)因为成等比数列,所以,
此时椭圆的离心率,
所以椭圆的离心率,因为,所以,
则该曲线是"优美猫眼曲线";
(2)证明:设直线的方程为,联立,消去
并整理得此时,
所以,则,
所以,同理得,所以为定值;
(3)设直线的方程为,联立,消去
并整理得因为直线与椭圆相切,
所以,解得,不妨取,
此时直线的方程,联立,消去并整理得
设,由韦达定理得,
所以,设,
设点到直线的距离为,则当,即时,取得最大值,最大值为.
则面积最大值
21.对于函数的导函数,若在其定义域内存在实数和,使得成立,称是“青峰”函数,并称是的“青峰值”.
(1)试分别判断函数,和,是不是“青峰”函数?并说明理由;
(2)若是“青峰”函数,且“青峰值”为2,求实数的取值范围;
(3)证明:是“青峰”函数,并求出该函数“青峰值”的取值范围.
【答案】(1)见解析 (2) (3)见解析
【解析】(1)函数是"卓然"函数,因为,
当时,则有,,满足;
因为,,当时,,而,
所以不可能成立,即不存在实数和,使得成立,
所以不是"卓然"函数;
(2)由题意可得,所以有解,
即有解,对于函数,
因为
所以,)
令,则,解得,,
单调递减区间:,故值域为:。
所以实数的取值范围是.
(3)证明:因为,
设,,,
当时,恒成立,此时不存在使得成立,不合题意;
当时,因为与在上均单调递减,
所以在上单调递减,所以在上单调递增,
因为,,
所以存在使,,
当时,单调递减,
当时,单调递增,
所以
由,所以,所以
此时不存在使得成立,不合题意;
当时,若,则,从而,所以在上单调递增,
当时,设,则,
设,当时,在上单调递增,且,
所以,从而,所以,从而,
所以在上单调递增,所以,
从而,所以在上单调递增,又,
由零点存在性定理可知,存在使得,
即成立,符合题意;当时,,显然存在零点符合题意;
当时,在上单调递减,
且,所以,从而,所以,从而,
所以在上单调递减,趋于时,趋于,
存在,使得,即,
当时,上单调递增,
当时,上单调递减,
又,当趋于时,趋于,由零点存在性定理,
存在使得,即成立,符合题意;
综上所述,为"卓然"函数,该函数"卓然"取值范围是.
2024.11
一、填空题(本大题共12题,满分54分,第1-6题每题4分,第7-12题每题5分)
1.若集合,则________.
2.已知向量,,若,则________.
3.若一元二次不等式的解集是,则的值是________.
4.直线与圆相交,所得的弦的长为________.
5.设事件,是互斥事件,且,则________.
6.设,,若,则的最大值为________.
7.从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有________种,(用数字填写答案)
8.设,若
,则________.
9.容量为的一组数据,它的第百分位数(为1到99之间的整数)各不相同,则的最小值为________.
10.若函数在区间上有最大值,则实数的取值范围是________.
11.已知,且是复数,当的最大值为3,则________.
12.已知平面向量,,满足与的夹角为锐角,,,,且的最小值为,向量的取值范围是________.
二、选择题(本大题共4题,满分18分,第13-14题每题4分,第15-16题每题5分)
13.已知是偶函数,则( )
A. B. C.1 D.2
14.2024年3月,树人中学组织三个年级的学生进行党史知识竞赛、经统计,得到前200名学生分布的饼状图(如图)和前200名中高一学生排名分布的频率条形图(如图),则下列命题错误的是( )
A.成绩前200名的200人中,高一人数比高二人数多30人
B.成绩第1-100名的100人中,高一人数不超过一半
C.成绩第1-50名的50人中,高三最多有32人
D.成绩第51-100名的50人中,高二人数比高一的多
15.如图,已知正三棱柱,,,分别是棱,上的点.记与所成的角为,与平面所成的角为,二面角的平面角为,则( )
A. B. C. D.
16.已知数列满足(为正整数),,设集合.有以下两个猜想:①不论取何值,总有;②若,且数列中恰好存在连续的7项构成等比数列,则的可能取值有6个.其中( ).
A.①正确,②正确 B.①正确,②错误
C.①错误,②正确 D.①错误,②错误
三、解答题
17.如图所示的几何体是圆锥的一半和一个三棱锥组成,圆锥底面圆的半径为1,圆锥的高,三棱锥的底面是以圆锥的底面圆的直径为斜边的等腰直角三角形,且与圆锥底面在同一个平面上.
(1)求直线和平面所成角的大小;
(2)求该几何体的体积.
18.在三角形中,内角,,所对边分别为,,,已知.
(I)求角的大小;
(2)若,三角形的面积为,求三角形的周长.
19.汽车智能辅助驾驶已得到广泛应用,其自动刹车的工作原理是用雷达测出车辆与前方障碍物之间的距离(并结合车速转化为所需时间),当此距离等于报警距离时就开始报警提醒,等于危险距离时就自动刹车、某种算法(如下图所示)将报警时间划分为4段,分别为准备时间、人的反应时间、系统反应时间、制动时间,相应的距离分别为、、、.当车速为(米/秒),且时,通过大数据统计分析得到下表(其中系数随地面湿滑程度等路面情况而变化,)
阶段 0、准备 1、人的反应 2、系统反应 3、制动
时间 秒 秒
距离 米 米
(I)请写出报警距离(米)与车速(米/秒)之间的函数关系式,并求时,若汽车达到报警距离时人和系统均不采取任何制动措施,仍以此速度行驶,则汽车撞上固定障碍物的最短时间。(精确到0.1秒)
(2)若要求汽车不论在何种路面情况下行驶,报警距离均小于80米,则汽车的行驶速度应限制在多少米/秒以下?合多少千米/小时(精确到1千米/小时)?
20.如图所示,由椭圆和椭圆组合而成的曲线,由图形特点,这里称曲线为“猫眼曲线”,特别地,若两个椭圆的离心率相等,则称其为“优美猫眼曲线”.
(1)已知猫眼曲线满足,,成等比数列,试判断该曲线是否为“优美猫眼曲线”;
(2)在曲线中,若,,,斜率为的直线不经过坐标原点,且与椭圆相交所得弦的中点为,与椭圆相交所得弦的中点为,证明:直线,的斜率之比为定值;
(3)在(2)的条件下,若直线的斜率,且与椭圆相切,与椭圆相交于,两点,为椭圆上异于,的任意一点,求面积的最大值.
21.对于函数的导函数,若在其定义域内存在实数和,使得成立,称是“青峰”函数,并称是的“青峰值”.
(1)试分别判断函数,和,是不是“青峰”函数?并说明理由;
(2)若是“青峰”函数,且“青峰值”为2,求实数的取值范围;
(3)证明:是“青峰”函数,并求出该函数“青峰值”的取值范围.
参考答案
一、填空题
1.; 2.; 3.; 4.; 5.; 6.; 7.; 8.; 9.; 10.; 11.; 12.;
11.已知,且是复数,当的最大值为3,则________.
【答案】
【解析】设是实数,则,,
综上,勺最大值为,即有.故答案为:.
12.已知平面向量,,满足与的夹角为锐角,,,,且的最小值为,向量的取值范围是________.
【答案】
【解析】设与的夹角为,则,
当,上式有最小值为,的最小值为
的最小值为3,,解得.
又,此时,,
与的夹角为,且
不妨设,
向量的取值范围是故答案为:
二、选择题
13.C; 14.D; 15.A; 16.A
15.如图,已知正三棱柱,,,分别是棱,上的点.记与所成的角为,与平面所成的角为,二面角的平面角为,则( )
A. B. C. D.
【答案】
【解析】正三棱柱中,正三棱柱的所有棱长相等,设棱长为1,如图,过作,垂足点为,连接,则,
与所成的角为,且,
又,与平面所成的角为,
且①
再过点作,垂足点为,连接,又易知底面底面,
,又平面
二面角的平面角为,且,
②,又,③
由①②③得,又在单调递增,
故选:.
16.已知数列满足(为正整数),,设集合.有以下两个猜想:①不论取何值,总有;②若,且数列中恰好存在连续的7项构成等比数列,则的可能取值有6个.其中( ).
A.①正确,②正确 B.①正确,②错误
C.①错误,②正确 D.①错误,②错误
【答案】
【解析】不妨设出数列中的一项,
①若被3除余1,则由已知可得,,
若被3除余2,则由已知可得,,
若被3除余0,则由已知可得,,
所以对对任意的,则,
所以对数列中的任一项,若,则,因为,所以,
所以数列中必存在某一项(否则与上述结论矛盾),若,结论得证,
若,则,,结论得证,若,则,得证,
所以,不论取何值,总有;故①正确;
②若是3的倍数,则,
若被3除余1,则由已知可得,,
若被3除余2,则由已知可得,,
所以连续的7项构成等比数列的公比为,
因为,所以这7项中前6项一定都量3的倍数,
而第七项一定不是3的倍数(否则构成等比数列的连接项数会多于7项),
设第7项为,则是被3除余1或余2的正整数,则可推得,
因为,所以,或,
由递推关系式可知,在该数列的前项中,满足小于等于2022的项只有;,或,或,
所以首项的有可能取值的集合为,,
故的可能取值有6个.故②正确.故选:.
三、解答题
17.(1) (2)
18.(1) (2)
19.(1);3.1秒 (2)20米/秒;72千米/小时
20.如图所示,由椭圆和椭圆组合而成的曲线,由图形特点,这里称曲线为“猫眼曲线”,特别地,若两个椭圆的离心率相等,则称其为“优美猫眼曲线”.
(1)已知猫眼曲线满足,,成等比数列,试判断该曲线是否为“优美猫眼曲线”;
(2)在曲线中,若,,,斜率为的直线不经过坐标原点,且与椭圆相交所得弦的中点为,与椭圆相交所得弦的中点为,证明:直线,的斜率之比为定值;
(3)在(2)的条件下,若直线的斜率,且与椭圆相切,与椭圆相交于,两点,为椭圆上异于,的任意一点,求面积的最大值.
【答案】(1)见解析 (2)见解析 (3)
【解析】(1)因为成等比数列,所以,
此时椭圆的离心率,
所以椭圆的离心率,因为,所以,
则该曲线是"优美猫眼曲线";
(2)证明:设直线的方程为,联立,消去
并整理得此时,
所以,则,
所以,同理得,所以为定值;
(3)设直线的方程为,联立,消去
并整理得因为直线与椭圆相切,
所以,解得,不妨取,
此时直线的方程,联立,消去并整理得
设,由韦达定理得,
所以,设,
设点到直线的距离为,则当,即时,取得最大值,最大值为.
则面积最大值
21.对于函数的导函数,若在其定义域内存在实数和,使得成立,称是“青峰”函数,并称是的“青峰值”.
(1)试分别判断函数,和,是不是“青峰”函数?并说明理由;
(2)若是“青峰”函数,且“青峰值”为2,求实数的取值范围;
(3)证明:是“青峰”函数,并求出该函数“青峰值”的取值范围.
【答案】(1)见解析 (2) (3)见解析
【解析】(1)函数是"卓然"函数,因为,
当时,则有,,满足;
因为,,当时,,而,
所以不可能成立,即不存在实数和,使得成立,
所以不是"卓然"函数;
(2)由题意可得,所以有解,
即有解,对于函数,
因为
所以,)
令,则,解得,,
单调递减区间:,故值域为:。
所以实数的取值范围是.
(3)证明:因为,
设,,,
当时,恒成立,此时不存在使得成立,不合题意;
当时,因为与在上均单调递减,
所以在上单调递减,所以在上单调递增,
因为,,
所以存在使,,
当时,单调递减,
当时,单调递增,
所以
由,所以,所以
此时不存在使得成立,不合题意;
当时,若,则,从而,所以在上单调递增,
当时,设,则,
设,当时,在上单调递增,且,
所以,从而,所以,从而,
所以在上单调递增,所以,
从而,所以在上单调递增,又,
由零点存在性定理可知,存在使得,
即成立,符合题意;当时,,显然存在零点符合题意;
当时,在上单调递减,
且,所以,从而,所以,从而,
所以在上单调递减,趋于时,趋于,
存在,使得,即,
当时,上单调递增,
当时,上单调递减,
又,当趋于时,趋于,由零点存在性定理,
存在使得,即成立,符合题意;
综上所述,为"卓然"函数,该函数"卓然"取值范围是.
同课章节目录
