7.2.1 三角函数的定义 课件(共20张PPT) 2024-2025学年人教B版(2019)高中数学必修第三册
文档属性
| 名称 | 7.2.1 三角函数的定义 课件(共20张PPT) 2024-2025学年人教B版(2019)高中数学必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 684.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-21 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
7.2.1 三角函数的定义
第七章 三角函数
1.理解任意角的正弦、余弦、正切的定义.
2.会求角的正弦、余弦、正切值.
3.掌握三角函数在各象限内的符号.
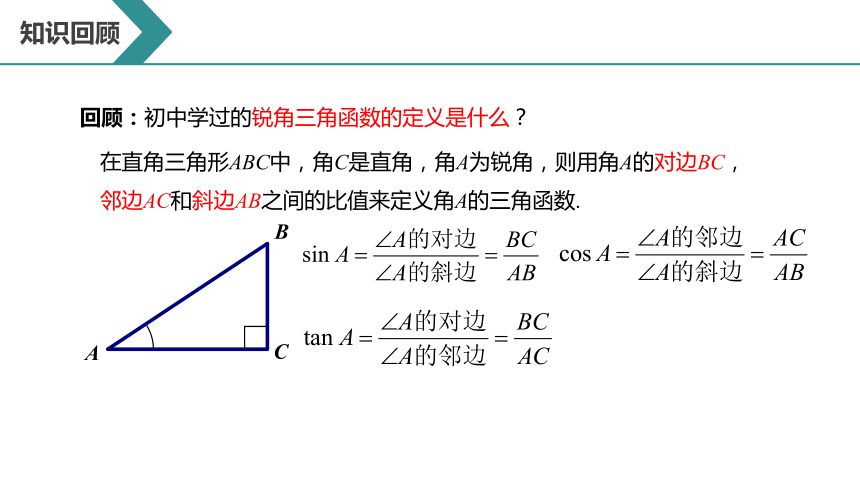
回顾:初中学过的锐角三角函数的定义是什么?
在直角三角形ABC中,角C是直角,角A为锐角,则用角A的对边BC,邻边AC和斜边AB之间的比值来定义角A的三角函数.
问题1:若α∈(0,),点P(3,4)在角α的终边上,由此能否求出sin α,cos α,tan α的值 若能求出,简述过程;若不能,请说明理由.
能.过点P作x轴的垂线,垂足为点M,则有OM=3,MP=4,OP==5,故sin α=,cos α=,tan α= .
问题2:上题中,若在角α的终边上另取一个不同于坐标原点的点P',则sin α,cos α,tan α的值有变化吗
没有变化.
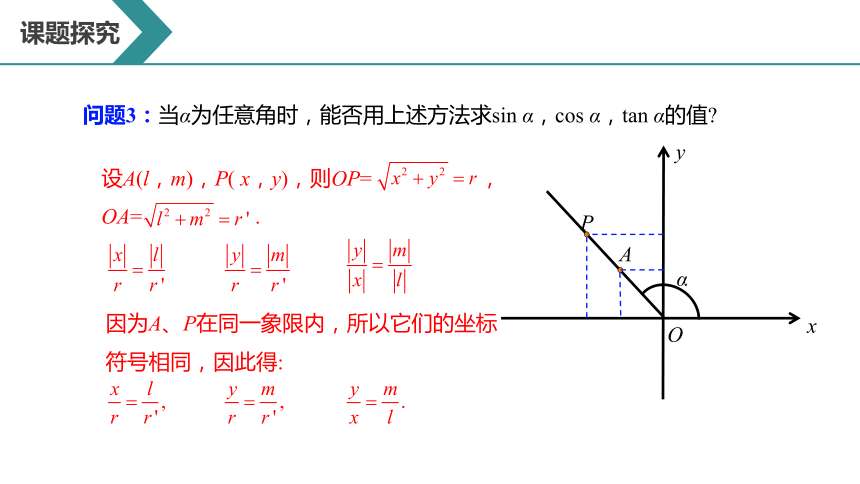
问题3:当α为任意角时,能否用上述方法求sin α,cos α,tan α的值
P
A
α
x
y
O
设A(l,m),P( x,y),则OP= ,
OA= .
因为A、P在同一象限内,所以它们的坐标符号相同,因此得:
x
y
O
P(x,y)
α的终边
对于任意角α来说,设P(x,y)是α终边上异于原点的任意一点,
r= ,称 为角α的正弦,记作sin α;
称 为角α的余弦,记作cos α,因此sin α= ,cos α= .
角α的正弦、余弦、正切都称为α的三角函数.
当角α的终边不在y轴上时,称 为角α的正切,记作tan α,即tan α= .
概念讲解
思考:三角函数是以什么为自变量,是以什么为函数值的函数?正弦、余弦、正切的定义域分别是什么?
正弦、余弦、正切函数都是以角为自变量,以比值为函数值的函数.(统称为三角函数)
弧度制下,角的集合与实数集R之间建立了一一对应关系.
三角函数可以看成以实数为自变量的函数.
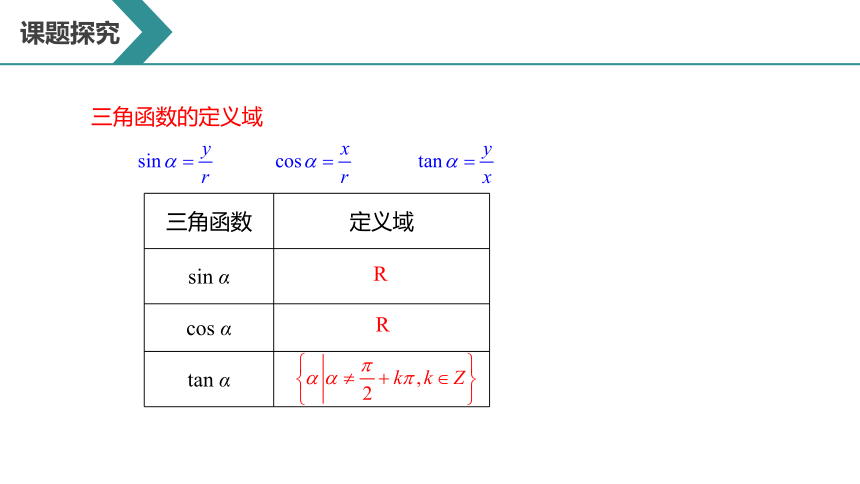
三角函数的定义域
三角函数 定义域
sin α
cos α
tan α
R
R
例1 已知角α的终边上一点P(1,-),求sin α,cos α,tan α的值.
例2 (1)若α=-,则sin α=________,cos α=________,tan α=________.
(2)若角θ的终边过点P(a,8),且cos θ=-,则a的值是( )
A.6 B.-6
C.10 D.-10
解析:(1)因为角-的终边与单位圆交于点P(,-),
所以sin α=-,cos α=,tan α=-.
-
-
(2)由任意角的三角函数的定义可知=-,解得a=±6.
显然a=6时不成立,所以a=-6.
B
方法总结
求任意角α的三角函数的步骤:
(1)取终边上一点P(x,y);
(2)求r, ;
(3)利用公式求sin α,cos α,tan α.
讨论:不求值,你能判断sin(-),cos(-),tan(-)的符号吗?
一全正、二正弦、三正切、四余弦
如图,将三种三角函数的值在各象限的符号填入相应位置的括号中,并说出填写的依据.
x
y
O
sin α
( )
+
( )
( )
x
y
O
cos α
( )
( )
( )
( )
x
y
O
tan α
( )
( )
( )
( )
+
–
–
+
–
+
+
+
–
–
–
思考:当角α的终边位于坐标轴上时,该角的正弦、余弦与正切的符号是什么?
sin α cos α tan α
x轴正半轴 = 0 >0 = 0
x轴负半轴 = 0 <0 = 0
y轴正半轴 >0 = 0 不存在
y轴负半轴 <0 = 0 不存在
例3 判断下列各式的符号.
(1)sin 1 020°cos 1 021°tan 1 022°;
(2)tan 191°-cos 191°;
(3)sin 2cos 3tan 4.
解:(1)∵1 020°=2×360°+300°,1 021°=2×360°+301°,
1 022°=2×360°+302°,∴它们都是第四象限角,
∴sin 1 020°<0,cos 1 021°>0,tan 1 022°<0,
∴sin 1 020°cos 1 021°tan 1 022°>0.
(2)∵191°角是第三象限角,∴tan 191°>0,cos 191°<0,
∴tan 191°-cos 191°>0.
(3)∵<2<π,<3<π,π<4<,
∴2是第二象限角,3是第二象限角,4是第三象限角,
∴sin 2>0,cos 3<0,tan 4>0,
∴sin 2cos 3tan 4<0.
(2)tan 191°-cos 191°;
(3)sin 2cos 3tan 4.
例4 设 sin θ < 0 且 tan θ > 0,确定 θ 是第几象限角.
解:因为 sin θ < 0,所以 θ 可能是第三、四象限的角;
又 tan θ > 0,θ 可能是第一、三象限的角;
综上所述,θ 是第三象限的角.
根据今天所学,回答下列问题:
(1)三角函数的定义是什么
(2)在三角函数中,任意角 α 分别需要满足怎样的条件?
(3)在三角函数中,角的终边与三角函数的符号有什么关系?
1.函数 的值域是( )
A.{-1,1} B.{-1,1,3}
C.{-1,3} D.{1,3}
2.已知角θ的终边上有一点P(-4a, 3a)(a≠0),则2sin θ+cos θ的值是( )
A. B.
C. 或 D.不确定
C
C
3.设A是第三象限角,且|sin |= -sin ,则 是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
4.若sin θ·cos θ>0, 则θ是第 象限的角.
D
一、三
7.2.1 三角函数的定义
第七章 三角函数
1.理解任意角的正弦、余弦、正切的定义.
2.会求角的正弦、余弦、正切值.
3.掌握三角函数在各象限内的符号.
回顾:初中学过的锐角三角函数的定义是什么?
在直角三角形ABC中,角C是直角,角A为锐角,则用角A的对边BC,邻边AC和斜边AB之间的比值来定义角A的三角函数.
问题1:若α∈(0,),点P(3,4)在角α的终边上,由此能否求出sin α,cos α,tan α的值 若能求出,简述过程;若不能,请说明理由.
能.过点P作x轴的垂线,垂足为点M,则有OM=3,MP=4,OP==5,故sin α=,cos α=,tan α= .
问题2:上题中,若在角α的终边上另取一个不同于坐标原点的点P',则sin α,cos α,tan α的值有变化吗
没有变化.
问题3:当α为任意角时,能否用上述方法求sin α,cos α,tan α的值
P
A
α
x
y
O
设A(l,m),P( x,y),则OP= ,
OA= .
因为A、P在同一象限内,所以它们的坐标符号相同,因此得:
x
y
O
P(x,y)
α的终边
对于任意角α来说,设P(x,y)是α终边上异于原点的任意一点,
r= ,称 为角α的正弦,记作sin α;
称 为角α的余弦,记作cos α,因此sin α= ,cos α= .
角α的正弦、余弦、正切都称为α的三角函数.
当角α的终边不在y轴上时,称 为角α的正切,记作tan α,即tan α= .
概念讲解
思考:三角函数是以什么为自变量,是以什么为函数值的函数?正弦、余弦、正切的定义域分别是什么?
正弦、余弦、正切函数都是以角为自变量,以比值为函数值的函数.(统称为三角函数)
弧度制下,角的集合与实数集R之间建立了一一对应关系.
三角函数可以看成以实数为自变量的函数.
三角函数的定义域
三角函数 定义域
sin α
cos α
tan α
R
R
例1 已知角α的终边上一点P(1,-),求sin α,cos α,tan α的值.
例2 (1)若α=-,则sin α=________,cos α=________,tan α=________.
(2)若角θ的终边过点P(a,8),且cos θ=-,则a的值是( )
A.6 B.-6
C.10 D.-10
解析:(1)因为角-的终边与单位圆交于点P(,-),
所以sin α=-,cos α=,tan α=-.
-
-
(2)由任意角的三角函数的定义可知=-,解得a=±6.
显然a=6时不成立,所以a=-6.
B
方法总结
求任意角α的三角函数的步骤:
(1)取终边上一点P(x,y);
(2)求r, ;
(3)利用公式求sin α,cos α,tan α.
讨论:不求值,你能判断sin(-),cos(-),tan(-)的符号吗?
一全正、二正弦、三正切、四余弦
如图,将三种三角函数的值在各象限的符号填入相应位置的括号中,并说出填写的依据.
x
y
O
sin α
( )
+
( )
( )
x
y
O
cos α
( )
( )
( )
( )
x
y
O
tan α
( )
( )
( )
( )
+
–
–
+
–
+
+
+
–
–
–
思考:当角α的终边位于坐标轴上时,该角的正弦、余弦与正切的符号是什么?
sin α cos α tan α
x轴正半轴 = 0 >0 = 0
x轴负半轴 = 0 <0 = 0
y轴正半轴 >0 = 0 不存在
y轴负半轴 <0 = 0 不存在
例3 判断下列各式的符号.
(1)sin 1 020°cos 1 021°tan 1 022°;
(2)tan 191°-cos 191°;
(3)sin 2cos 3tan 4.
解:(1)∵1 020°=2×360°+300°,1 021°=2×360°+301°,
1 022°=2×360°+302°,∴它们都是第四象限角,
∴sin 1 020°<0,cos 1 021°>0,tan 1 022°<0,
∴sin 1 020°cos 1 021°tan 1 022°>0.
(2)∵191°角是第三象限角,∴tan 191°>0,cos 191°<0,
∴tan 191°-cos 191°>0.
(3)∵<2<π,<3<π,π<4<,
∴2是第二象限角,3是第二象限角,4是第三象限角,
∴sin 2>0,cos 3<0,tan 4>0,
∴sin 2cos 3tan 4<0.
(2)tan 191°-cos 191°;
(3)sin 2cos 3tan 4.
例4 设 sin θ < 0 且 tan θ > 0,确定 θ 是第几象限角.
解:因为 sin θ < 0,所以 θ 可能是第三、四象限的角;
又 tan θ > 0,θ 可能是第一、三象限的角;
综上所述,θ 是第三象限的角.
根据今天所学,回答下列问题:
(1)三角函数的定义是什么
(2)在三角函数中,任意角 α 分别需要满足怎样的条件?
(3)在三角函数中,角的终边与三角函数的符号有什么关系?
1.函数 的值域是( )
A.{-1,1} B.{-1,1,3}
C.{-1,3} D.{1,3}
2.已知角θ的终边上有一点P(-4a, 3a)(a≠0),则2sin θ+cos θ的值是( )
A. B.
C. 或 D.不确定
C
C
3.设A是第三象限角,且|sin |= -sin ,则 是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
4.若sin θ·cos θ>0, 则θ是第 象限的角.
D
一、三
