7.2.2 单位圆与三角函数线 课件(共19张PPT) 2024-2025学年人教B版(2019)高中数学必修第三册
文档属性
| 名称 | 7.2.2 单位圆与三角函数线 课件(共19张PPT) 2024-2025学年人教B版(2019)高中数学必修第三册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-21 22:23:47 | ||
图片预览





文档简介
(共19张PPT)
第七章 三角函数
7.2.2 单位圆与三角函数线
人教B版(2019)必修第三册
1.理解单位圆的概念.
2.理解三角函数线的定义并能运用三角函数线解决相关问题.
什么是圆 圆的两大要素是什么
平面内到定点的距离等于定长的点的集合称为圆;圆心和半径是圆的两大要素.
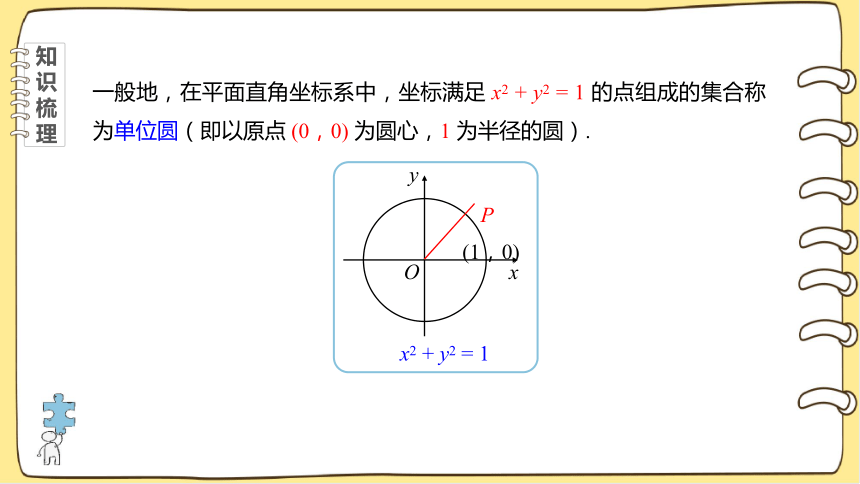
问题1:如图,若选取的 P 点的坐标满足 x2 + y2 = 1,说说其中 x2 + y2 = 1 的几何意义是什么?
因为 x2 + y2 = 1 可化为 = 1,
因此 P (x,y) 到原点 (0,0) 的距离为 1,
即 P (x,y) 的轨迹是以原点 (0,0) 为圆心,1 为半径的圆.
x
y
O
P
x2 + y2 = 1
一般地,在平面直角坐标系中,坐标满足 x2 + y2 = 1 的点组成的集合称为单位圆(即以原点 (0,0) 为圆心,1 为半径的圆).
x
y
O
P
x2 + y2 = 1
(1,0)
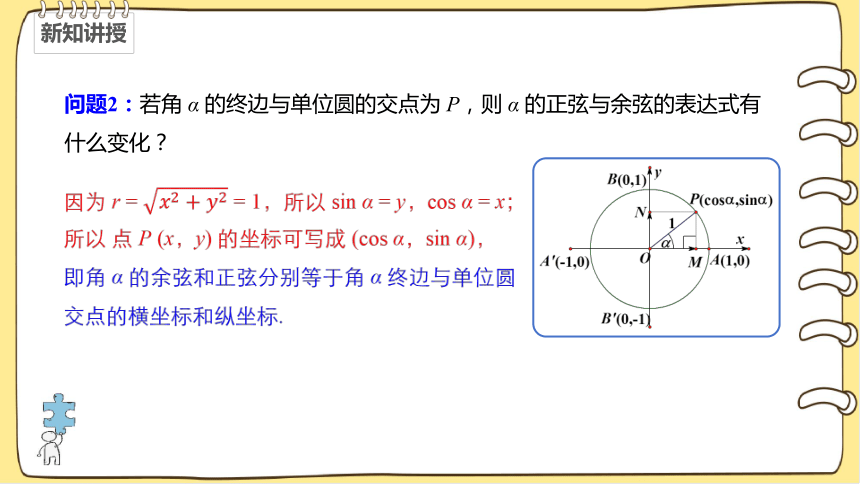
问题2:若角 α 的终边与单位圆的交点为 P,则 α 的正弦与余弦的表达式有什么变化?
因为 r = = 1,所以 sin α = y,cos α = x;
所以 点 P (x,y) 的坐标可写成 (cos α,sin α),
即角 α 的余弦和正弦分别等于角 α 终边与单位圆交点的横坐标和纵坐标.
问题3:你能给出任意角正弦和余弦的一个直观表示吗?
如图,过P作PM垂直x轴于点M,
可以直观地表示,称为角的余弦线;
可以直观地表示,称为角的正弦线.
o
P(x,y)
x
M
y
若 α 的终边不在 y 轴上,且 P (x,y) 是 α 终边上异于原点的任意一点,则 tan α = ;取坐标满足 x = 1 的点 P,则 tan α = y.
如图,设 α 的终边与直线 x = 1 交于点 T,则称
为角 α 的正切线.
x
y
O
T
A
1
α 的终边
思考:角α是第二象限的角时能否找到一个垂直于x轴的向量,使其数量为?
y
o
α的终边
A1
T1(-1,y1 )
A
·
x
取T1的坐标为(-1,y1),则
tanα=
追问:能否找到一个以A点为起点在过A的切线上的向量,使这一向量的数量为 ?
T′
角终边的反向延长线与切线交点为T′
一般结论:角α的正切等于角α的终边或其反向延长线与直线的交点的纵坐标.
正弦线、余弦线和正切线都称为三角函数线.
例1 作出- 的正弦线、余弦线和正切线.
解:在直角坐标系中作单位圆,如图,
以Ox轴为始边作-角,角的终边与单位圆交于点P,
作PM⊥Ox轴,垂足为M,
由单位圆与Ox轴正方向的交点A作Ox轴的垂线,与OP的反向延长线交于T点,
则sin -=MP,cos -=OM,tan -π=AT,
即-的正弦线为,余弦线为,正切线为.
方法归纳
1.作正弦线、余弦线时,首先找到角的终边与单位圆的交点,然后过此交点作x轴的垂线,得到垂足,从而得到正弦线和余弦线.
2.作正切线时,应从A(1,0)点引单位圆的切线交角的终边于一点T,即可得到正切线,要特别注意,当角的终边在第二或第三象限时,应将角的终边反向延长,再按上述作法来作正切线.
例2 在单位圆中画出适合下列条件的角α的终边.
解:(1)作直线y=交单位圆于点P,Q,则OP与OQ为角α的终边,如图①.
(2)作直线x=-交单位圆于点M,N,则OM与
ON为角α的终边,如图②.
(3)在直线x=1上截取AT=2,其中A的坐标为(1,0).设直线OT与单位圆交于点C,D,则OC与OD为角α的终边,如图③.
例3 cos 1,sin 1,tan 1的大小关系是( )
A.sin 1C.cos 1解析:作出单位圆,用三角函数线进行求解.
如图所示,有OMD
变式:利用三角函数线比较下列各组数的大小:
解:如图,画出角 与 的正弦线、余弦线、正切线,
sin =M1P1,sin =M2P2,tan =AT1,tan =AT2,
cos =OM1,cos =OM2,
由图形观察可得:M1P1>M2P2,AT1OM2,
∴(1)sin >sin ;(2)tancos .
利用单位圆中的三角函数线比较三角函数值的大小时,分三步:
(1)作出角的终边与单位圆的交点.
(2)作出三角函数线.
(3)比较三角函数线的长度,同时要注意方向.
方法归纳
1.下列四个命题中(1)α一定时,单位圆中的正弦线一定;(2)单位圆中有相同正弦线的角相等;(3)α与α+π有相同的正切线;(4)具有相同正切线的两个角终边在同一条直线上.不正确的命题个数是( )
A.0 B.1 C.2 D.3
2.已知α是第一象限角,则下列等式中可能成立的是( )
A.sin α+cos α=1.2 B. sin α+cos α=-0.9
C.sin αcos α=1.3 D.sin α+cos α=-1.2
C
A
3.角和角有相同的( )
A.正弦线 B.余弦线
C.正切线 D.不能确定
4.(多选)下列不等式成立的是( )
A.sin 1C.tan 1C
AD
回顾:本课关键词“单位圆、三角函数线” ,说说今天学了哪些知识?
第七章 三角函数
7.2.2 单位圆与三角函数线
人教B版(2019)必修第三册
1.理解单位圆的概念.
2.理解三角函数线的定义并能运用三角函数线解决相关问题.
什么是圆 圆的两大要素是什么
平面内到定点的距离等于定长的点的集合称为圆;圆心和半径是圆的两大要素.
问题1:如图,若选取的 P 点的坐标满足 x2 + y2 = 1,说说其中 x2 + y2 = 1 的几何意义是什么?
因为 x2 + y2 = 1 可化为 = 1,
因此 P (x,y) 到原点 (0,0) 的距离为 1,
即 P (x,y) 的轨迹是以原点 (0,0) 为圆心,1 为半径的圆.
x
y
O
P
x2 + y2 = 1
一般地,在平面直角坐标系中,坐标满足 x2 + y2 = 1 的点组成的集合称为单位圆(即以原点 (0,0) 为圆心,1 为半径的圆).
x
y
O
P
x2 + y2 = 1
(1,0)
问题2:若角 α 的终边与单位圆的交点为 P,则 α 的正弦与余弦的表达式有什么变化?
因为 r = = 1,所以 sin α = y,cos α = x;
所以 点 P (x,y) 的坐标可写成 (cos α,sin α),
即角 α 的余弦和正弦分别等于角 α 终边与单位圆交点的横坐标和纵坐标.
问题3:你能给出任意角正弦和余弦的一个直观表示吗?
如图,过P作PM垂直x轴于点M,
可以直观地表示,称为角的余弦线;
可以直观地表示,称为角的正弦线.
o
P(x,y)
x
M
y
若 α 的终边不在 y 轴上,且 P (x,y) 是 α 终边上异于原点的任意一点,则 tan α = ;取坐标满足 x = 1 的点 P,则 tan α = y.
如图,设 α 的终边与直线 x = 1 交于点 T,则称
为角 α 的正切线.
x
y
O
T
A
1
α 的终边
思考:角α是第二象限的角时能否找到一个垂直于x轴的向量,使其数量为?
y
o
α的终边
A1
T1(-1,y1 )
A
·
x
取T1的坐标为(-1,y1),则
tanα=
追问:能否找到一个以A点为起点在过A的切线上的向量,使这一向量的数量为 ?
T′
角终边的反向延长线与切线交点为T′
一般结论:角α的正切等于角α的终边或其反向延长线与直线的交点的纵坐标.
正弦线、余弦线和正切线都称为三角函数线.
例1 作出- 的正弦线、余弦线和正切线.
解:在直角坐标系中作单位圆,如图,
以Ox轴为始边作-角,角的终边与单位圆交于点P,
作PM⊥Ox轴,垂足为M,
由单位圆与Ox轴正方向的交点A作Ox轴的垂线,与OP的反向延长线交于T点,
则sin -=MP,cos -=OM,tan -π=AT,
即-的正弦线为,余弦线为,正切线为.
方法归纳
1.作正弦线、余弦线时,首先找到角的终边与单位圆的交点,然后过此交点作x轴的垂线,得到垂足,从而得到正弦线和余弦线.
2.作正切线时,应从A(1,0)点引单位圆的切线交角的终边于一点T,即可得到正切线,要特别注意,当角的终边在第二或第三象限时,应将角的终边反向延长,再按上述作法来作正切线.
例2 在单位圆中画出适合下列条件的角α的终边.
解:(1)作直线y=交单位圆于点P,Q,则OP与OQ为角α的终边,如图①.
(2)作直线x=-交单位圆于点M,N,则OM与
ON为角α的终边,如图②.
(3)在直线x=1上截取AT=2,其中A的坐标为(1,0).设直线OT与单位圆交于点C,D,则OC与OD为角α的终边,如图③.
例3 cos 1,sin 1,tan 1的大小关系是( )
A.sin 1
如图所示,有OM
变式:利用三角函数线比较下列各组数的大小:
解:如图,画出角 与 的正弦线、余弦线、正切线,
sin =M1P1,sin =M2P2,tan =AT1,tan =AT2,
cos =OM1,cos =OM2,
由图形观察可得:M1P1>M2P2,AT1
∴(1)sin >sin ;(2)tan
利用单位圆中的三角函数线比较三角函数值的大小时,分三步:
(1)作出角的终边与单位圆的交点.
(2)作出三角函数线.
(3)比较三角函数线的长度,同时要注意方向.
方法归纳
1.下列四个命题中(1)α一定时,单位圆中的正弦线一定;(2)单位圆中有相同正弦线的角相等;(3)α与α+π有相同的正切线;(4)具有相同正切线的两个角终边在同一条直线上.不正确的命题个数是( )
A.0 B.1 C.2 D.3
2.已知α是第一象限角,则下列等式中可能成立的是( )
A.sin α+cos α=1.2 B. sin α+cos α=-0.9
C.sin αcos α=1.3 D.sin α+cos α=-1.2
C
A
3.角和角有相同的( )
A.正弦线 B.余弦线
C.正切线 D.不能确定
4.(多选)下列不等式成立的是( )
A.sin 1
AD
回顾:本课关键词“单位圆、三角函数线” ,说说今天学了哪些知识?
